二维装箱问题的遗传算法求解*

田大肥 申 喜 周 巍

(中国舰船研究设计中心 武汉 430064)

二维装箱问题的遗传算法求解*

田大肥 申 喜 周 巍

(中国舰船研究设计中心 武汉 430064)

通过分析人工排列的思考过程和实际经验,提出一种解决二维规则物体排列问题的算法。通过计算可放置点和可放置空间,高效解决物块的排列问题。应用遗传算法,求得最优的排列方案。实际应用证明了该算法的有效性。

二维装箱; 可放置点; 可放置空间; 遗传算法

Class Number TP391.7

1 引言

二维装箱问题是随着计算机技术的产生而出现的,大量出现在机械制造、皮革服装加工、汽车、造船、货物装载以及大规模集成电路板的设计等领域[1]。排样布局的优劣直接与材料的成本及经济效益相关。目前主要存在的问题是材料的利用率偏低,造成巨大的浪费。对于规模较大的生产厂家来说,即使是材料利用率有很小的提升,也会带来巨大的经济效益。

根据目标的不同,二维装箱问题可以分为以下几类:

· 箱柜装载问题(bin packing problem):给定一些不同类型的矩形箱子和一些规格一致的矩形容器,问题是要把所有箱子装入最少数量的容器中。

· 容器装载问题(container packing problem):所有箱子要装入一个宽度为有限数值的矩形容器,它的高度不限,要求将所有物品放入容器中,并取得最小的放置高度,使容器利用率最高。

· 背包装载问题[2](knapsack loading problem):每个箱子有一定的价值,背包装载是选择箱子的一部分装入容器中,使得装入容器中的箱子总价值最大[3]。

本文主要研究第二类装箱问题。

目前提出的基于遗传算法的装箱算法主要有BL(bottom left)算法、下台阶算法、最低水平线算法和基于最低水平线的搜索算法。其中下台阶算法是在BL算法的基础上的改进,最低水平线算法又在此基础上改进,基于最低水平线的搜索算法则是在最低水平线算法基础上又提出的改进[4～6]。本文提出一种新的排列方法,通过对多组实验结果进行测试比较,证明了本文算法的有效性。

2 问题描述

对于所要研究的二维装箱问题,可作如下抽象:给定一个矩形容器A,其宽度和高度分别为W和H。另有n个矩形物块,其宽度和高度分别为wi,hi(i=1,2,…,n)。确定排列方案,将所有物块放入矩形箱子,并使其所占用的空间最小。

排列过程中须满足以下要求:

1) 放入的任意物块的任意部分均不超出箱子边界。

2) 任意两个物块的任意部分互不重叠[7]。

3 装箱算法

在人工排列的过程中,为了使物块占用的空间最小,我们总是试图将物块放置在尽可能低,且尽可能靠左的位置。在将物块放得尽可能低的过程中,物块最终会受到之前放入的物块的上边缘或是箱子底面边界的阻挡。在将物块放得尽可能靠左的过程中,物块最终也会受到之前放入的物块的右侧边缘或是箱子左侧边界的阻挡。作为物块的左侧边与下侧边的交点,其左下角点在放置过程中会同时受到之前放入的物块的上边缘或是箱子底面边界和之前放入的物块的右边缘或是箱子左侧边界的阻挡。所以在放置物块的过程中,会以其左下角点作为参考点(reference point)。

3.1 可放置点

以箱子的左下角点为原点,以箱子的底边为x轴,以箱子左侧边为y轴。在放入第一个物块时,坐标原点为坐标系中唯一的可放置点(available point)。在放入第一个物块之后,位于坐标原点的可放置点被占用,同时在物块的右下角点和左上角点产生两个新的可放置点。第一个放入的物块的宽度和高度分别为w1和h1,则产生的两个可放置点坐标为(w1,0)、(0,h1)。假设第二个箱子占用了点(w1,0),则删除(w1,0)点,同时增加因物块的右侧面而产生的可放置点(w1+w2,0)。至于物块的上侧面产生的可放置点,应当有以下几种情况:

1) 如果h2>h1,则产生可放置点(0,h2);

2) 如果h2=h1,则产生的可放置点与第一个物块产生的可放置点(0,h1)重合;

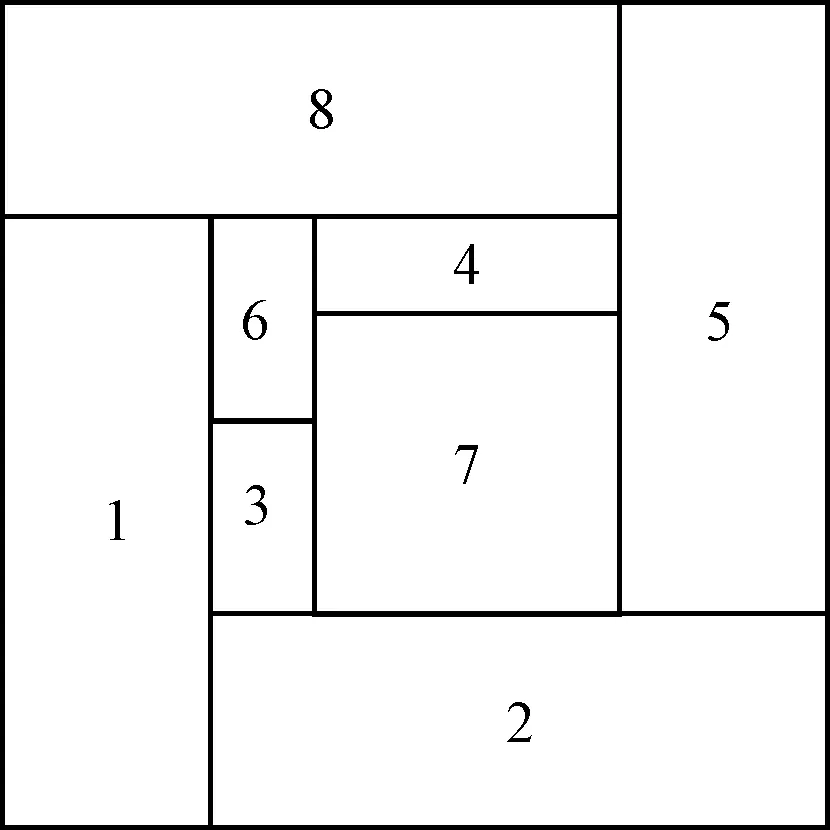
3) 如果h2

从放置过程中可以看出,在放入一个物块的过程中,占用了一个可放置点,同时最多增加二个可放置点。因此,考虑第i个箱子时,最多有i个可放置点。而在实际操作过程中我们发现,由于重叠等情况的出现,可放置点通常会少于i个。

图1 可放置点

3.2 可放置空间

为了将物块放入某个可放置点,需要该点在x轴方向和y轴方向有足够的空间,至少能够容纳物块的宽度和高度。将x轴方向的可放置空间(available space)称为x空间,将y轴方向的可放置空间称为y空间。一般情况下x空间为从可放置点的横坐标开始,一直向右延伸直到接触到已放入物块的侧面或是箱子的壁为止的这段距离。同样,y空间为从可放置点的纵坐标开始,一直向上延伸直到接触到已放入物块的底面或是箱子的壁为止的这段距离。

图2 可放置空间

在得到了可放置空间之后,物块的放置过程就变成了简单的排序与比较过程,不需要将物块放入某个可放置点,就能检验其是否合适放入该点。极大地简化了计算过程,提高了计算速度。

3.3 可放置点的刷新

在放入一个新的物块之后,会产生新的可放置点,这就需要对可放置点的集合进行刷新。同时在放入物块的过程中,有些可放置点虽然没有被占用,但会被物块覆盖,这种情况下就需要对可放置点的坐标进行调整。对可放置点进行调整的过程中,也需要对可放置空间进行调整,这个过程称为可放置点的刷新(renovation of available points)。

尤其需要说明的是,可放置点不会因为被覆盖或是被阻挡而删除,只是其x坐标或是y坐标以及x空间或是y空间会受到影响。可放置点只会因为以下几种原因被删除:

1) 被放入的物块占用;

2) 因放入物块的影响使得可放置点的x空间小于尚未放入的物块中最小的宽度值,或是可放置点的y空间小于尚未放入的物块中最小的高度值;

3) 后放入的物块产生的可放置点与现有的可放置点出现重叠,则删除其中的一个。

图3 可放置点的刷新

这样就使一些没有被当前放入的物块利用就被封闭在了一个小空间里,但依然有希望被后续放入的物块利用的可放置点得以保留。这样做可以有效地提高空间的利用率,同时降低对放置顺序的敏感性,可以更快地接近最优的排列方案。这也是本算法的重要特点。

3.4 装箱算法

综上,我们可以得到2D-packing算法。算法以物块集合B={b1,b2,…,bn}为输入,返回此次排列得到的空间利用率,用use表示可放置点的集合,矩形容器的宽度和高度分别为W和H。

算法:2D-packing(B)

初始可放置点use=[0,0,W,H];

For i=1:n

待放置物块的宽度为wi,高度为hi;

use按x坐标和y坐标由小到大顺序排列;

use中有m个可放置点;

Forj=1:m

If 第j个可放置点的x空间≥wi且y空间≥hi

返回j

End

End

占用第j个可放置点;

计算右侧边产生的可放置点;

计算该点的可放置空间;

计算上侧面产生的可放置点;

计算该点的可放置空间;

将新产生的可放置点放入use集合的末尾;

Fork=r:-1:1

分别计算对各可放置点及可放置空间的影响;

End

End

计算所有物块的面积和;

返回所有物块中最大的y坐标;

计算空间利用率。

在该算法中,初始可放置点为坐标原点,可放置空间为箱子的宽度和高度,按顺序放置每个物块。将所有可放置点分别按x坐标和y坐标由小到大排列,依次检测每个可放置点的x空间和y空间能否容纳将要放入的物块,选择占用第一个满足要求的可放置点。然后计算物块产生的新的可放置点,向可放置点集合中加入新产生的点并删除已经占用的点。计算新放入的物块对其他可放置点及其可放置空间的影响。算法结束时,返回该排列方案对应的空间利用率,即装箱物块的总面积对箱子面积的比率。

4 遗传算法求解过程

遗传算法的主要运算过程如下:

1) 编码:解空间中的解数据x,作为遗传算法的表现型形式。从表现型到基因型的映射称为编码。遗传算法在进行搜索之前先将解空间的解数据表示成遗传空间的基因型串结构数据,这些串结构数据的不同组合就构成了不同的点。在本算法中,将每一种排列方案编码成一个二进制字符串。

2) 初始群体的生成:随机产生N个初始串结构数据,每个串结构数据称为一个个体,N个个体构成了一个群体。遗传算法以这N个串结构作为初始点开始迭代。设置进化代数计数器t←0;设置最大进化代数T;随机生成M个个体作为初始群体P(0)。

3) 适应度值评价检测:适应度函数表明个体或解的优劣性。对于不同的问题,适应度函数的定义方式不同。根据具体问题,计算群体P(t)中各个个体的适应度。在本算法中,空间利用率是最重要的适应度评价标准。

4) 选择:将选择算子作用于群体。

5) 变异:将交叉算子作用于群体。

6) 变异:将变异算子作用于群体。

群体P(t)经过选择、交叉、变异运算后得到下一代群体P(t+1)。

7) 终止条件判断:若t≤T,则t←t+1,转到步骤2);若t>T,则以进化过程中所得到的具有最大适应度的个体作为最优解输出,终止运算[8～10]。

遗传算法有三个基本操作:选择(selection)、交叉(crossover)和变异(mutation)。

1) 选择。选择的目的是为了从当前群体中选出优良的个体,使它们有机会作为父代为下一代繁殖子孙。根据各个个体的适应度值,按照一定的规则或方法从上一代群体中选择出一些优良的个体遗传到下一代群体中。遗传算法通过选择运算体现这一思想,进行选择的原则是适应性强的个体为下一代贡献一个或多个后代的概率大。这就体现了达尔文的适者生存原则。

2) 交叉。交叉操作是遗传算法中最主要的遗传操作。通过交叉操作可以得到新一代个体,新个体组合了父辈个体的特性。将群体内的各个个体随机搭配成对,对每一个个体,以某个概率交换它们之间的部分染色体。交叉体现了信息交换的思想。

3) 变异。变异操作首先在群体中随机选择一个个体,对于选中的个体以一定的概率随机改变串结构数据汇总某个串的值,即对群体中的每一个个体,以某一概率改变某一个或某一些基因座上的基因值为其他的等位基因。同生物界一样,遗传算法中变异发生的概率很低。变异为新个体的产生提供了机会[11～12]。

5 算例分析

为测试算法的性能,本文对文献[13]中提到的BL算法无法解决的图形排列问题及文献[13]中的算例进行求解。

算例1 将一个8×8的方形分成8个大小不完全相等的小矩形。如图4所示,其对应的编码也已经标注在图4上。如果用BL算法,即使遍历所有的排列方案,也不可能得到最优排样图。用本文算法,可以很容易地得到图5所示的排样结果,对应的装入顺序为Popt={1,2,3,7,5,6,4,8}。

图4 最优排样图

图5 得到的一个最优解

算例2 对于文献[14]中的算例,将一个40×15的矩形分成25个大小不完全相等的小矩形。如图6所示,其对应的编码已经标注在图6上。现以宽度为40,高度不限的箱子为例,将分成的25个物块放入箱中,求解最小的排样高度。文献[14]在第2000代终止时得到的高度为17,应用本文算法,在群体规模与文献[14]同样为m=20的情况下,取交叉概率为1,单点交叉与双点交叉各占一半,变异概率pm1=pm2=0.3,在100代内终止时能够求得高度为17的排列结果。如图7所示,对应的装入顺序为Popt={2,9,20,25,22,19,12,5,11,10,3,8,6,17,7,23,15,21,16,14,1,18,13,4,24}

图6 最优排样图;高度15

图7 进化100代得到的一个最优解;高度17

6 结语

本文对二维空间布局问题进行了研究,提出了新的解决方法。从目前的实验结果来看,本文算法更为简便高效。而且此方法经过适当的改动之后,可以应用于箱柜装载问题(bin packing problem)和三维空间内的装箱问题,同时也可以应用于有瑕疵材料的下料问题。

[1] Lodi A, Martello S, Vigo D. A Unified Tabu Search Code for Multi-Dimensional Bin Packing Problems[J]. Annals of Operations Research,2004,131:203-213.

[2] 乐天.遗传算法求解0/1背包问题的综述[J].浙江海洋学院学报(自然科学版),2013,32(1):71-74.

[3] 张德福,魏丽军,陈青山,等.三维装箱问题的组合启发式算法[J].软件学报,2007,18(9):2083-2089.

[4] 郝洪霆.有瑕疵材料二维下料问题的研究和应用[D].济南:山东大学,2008.

[5] 刘艳娟.二维装箱问题的启发式算法研究[D].厦门:厦门大学,2007.

[6] 李玉贤.利用混合单亲遗传算法求解二维装箱问题[D].内蒙古:内蒙古大学,2011.

[7] 黄少丽,杨剑,侯桂玉,等.解决二维下料问题的顺序启发式算法[J].计算机工程与应用,2011,47(13):234-237.

[8] 赵新超,韩宇,艾文宝.求解背包问题的一种改进遗传算法[J].计算机工程与应用,2011,47(24):88-89.

[9] 王秋芬,梁道雷.一种求解0/1背包问题的启发式遗传算法[J].计算机应用与软件,2013,30(2):33-37.

[10] 田建立,晁学鹏.求解0/1背包问题的混沌遗传算法[J].计算机应用研究,2011,28(8):131-133.

[11] 雷英杰,张善文,李续武,等.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2011:11-13.

[12] 王丽娟.用单亲遗传算法求解二维装箱问题[D].内蒙古:内蒙古大学,2012.

[13] 贾志欣,殷国富,罗阳.二维不规则零件排样问题的遗传算法求解[J].计算机辅助设计与图形学学报,2001,14(5):467-470.

[14] Stefan Jokobs. On Genetic Algorithms for the Packing of Polygons[J]. European Journal of Operational Research,1996,88:165-181.

Genetic Algorithm of Two-Dimensional Container Packing

TIAN Dafei SHEN Xi ZHOU Wei

(China Ship Develop and Design Center, Wuhan 430064)

By analyzing the process and experience of human packing, an algorithm for solving two-dimensional packing is proposed. Packing problem is solved with high efficiency by creating and calculating the available points and available spaces. Genetic algorithm is used to get optimal arrangement. Practical applications show the validity and efficiency of the algorithm.

two-dimensional packing, available point, available space, genetic algorithm

2013年7月8日,

2013年8月21日

国防科工局基础科研重点项目(编号:A0820110001)资助。

田大肥,男,硕士研究生,研究方向:舰船总体研究与设计。申喜,男,硕士研究生,研究方向:舰船电力系统的优化设计。周巍,女,硕士,研究员,研究方向:舰船总体研究与设计。

TP391.7

10.3969/j.issn1672-9730.2014.01.016