基于位变性及结构特征效应的机床滑枕挠度误差预估模型*

康俊贤，王 军，，刘傲翔，舒启林

(1.沈阳建筑大学 交通与机械工程学院，沈阳 110168;2. 沈阳理工大学 机械工程学院，沈阳110159)

0 引言

目前，滑枕已作为重要运动部件被应用于机床的镗削结构中，镗削过程中滑枕伸出呈悬臂状态对工件进行加工［1］。因滑枕尺寸、自重及其它结构特征，加之镗削力、滑枕内部镗轴及其它部件重力的作用，可使滑枕悬伸端在反重力方向的静刚度不足而产生挠度;且加工过程中滑枕沿其中心轴线方向的运动使刀具中心点在广义加工空间［2］内的位置连续变化，进而使滑枕挠度呈连续性、位变性及静态非线性，这破坏了机床的几何精度，从而引起加工误差［3-4］;因此，如何精确表征上述因素影响下的滑枕挠度误差对滑枕的结构优化、误差补偿等起着举足轻重的作用。

目前，国内外对滑枕挠度误差的表征方法主要有实验测量法［4-5］、仿真拟合法［3，6］及预估模型法［7］。实验测量法以实体机床或样机的滑枕为测量对象，采用特定的现场检测技术，并对检测结果进行误差分离后可获得间隔行程下滑枕的挠度误差模型;该方法准确度颇高，但实体设备条件是其制约因素，且其检测方法及误差分离方法仍存疑、难点［8-9］。仿真拟合法以滑枕的数字化模型为研究对象，通过静力学仿真得到滑枕间隔行程的挠度值，进一步将其拟合后获得滑枕挠度与连续行程之间的关系;该方法准确度较高，其关键在于仿真过程中模型的合理程度以及拟合过程中拟合参数、结果的评定准则，这两项因素相互作用，共同制约着仿真准确度［10］。预估模型法以滑枕的设计方案及部分设计参数为研究基础，通过理论分析及计算得出滑枕挠度模型;该方法可在方案及图纸设计阶段即可实现对滑枕挠度信息的预估，较实验测量法节省了大量时间、人力及物力，且避免了仿真拟合法繁复的有限元及数据处理过程，其关键点及难点在于对滑枕方案及设计参数的理论分析过程及所建立模型的精度。绝大多数学者将特定型号机床设备的滑枕视为悬臂梁模型，并对该模型下的滑枕挠度进行理论分析及计算，但简化程度过高导致模型精度降低，且此类模型局限于特定型号的机床设备，其广泛适用性仍有待考证。

基于上述研究现状，本文以滑枕挠度为研究对象，以其广泛适用性为出发点，考虑滑枕在工作过程中的位变性及结构特征效应，构建一种更加符合实际工况的滑枕挠度误差预估模型;并进一步以特定型号的镗铣机床为例，验证了该模型的有效性。

1 滑枕挠度误差模型

本文将以包含滑枕方案设计、基本尺寸及重要结构特征参数等的设计模型为研究对象，根据叠加原理及悬臂梁、材料各向同性等假设，获得以广泛适用性为出发点的各类载荷条件下的滑枕挠度曲线，并融合结构特征效应于截面惯性矩的表征过程中，从而获得瞬时空间下的综合挠度曲线模型，进一步通过设参考点、加权、代换等方法将连续性、位变性引入该模型，即可获得基于位变性及结构特征效应的滑枕挠度误差预估模型。

1.1 滑枕模型

滑枕结构设计方案的多样性较强，但其形式主要有方滑枕及圆滑枕两种［11］。通常将主轴、传动件及其他附属部件置于其内部空腔或附着在其壁上，故在满足使用要求的前提下须在滑枕壁上设计形状开口(一般为矩形开口)便于装配、维修等工作的进行;此外，在滑枕内、外部常设有加强筋以提高其刚度从而减小变形量;因此，形状开口及筋板为滑枕的主要结构特征。滑枕的长度及行程是其轴向方向的两项基本尺寸参数;而垂直于轴向的截面尺寸则因滑枕形式而异，圆滑枕内外壁的径向尺寸、方滑枕内外壁的宽高尺寸及其各自所确定的壁厚尺寸则是基本截面尺寸参数。以方滑枕为例的主要结构特征及基本尺寸参数如图1 所示。

在挠度误差模型构建过程中，通常将瞬时空间状态［12］下的滑枕视为悬臂梁，如图2 所示，l为悬伸长度，ω 为悬臂梁最大挠度，θ 为端截面转角。

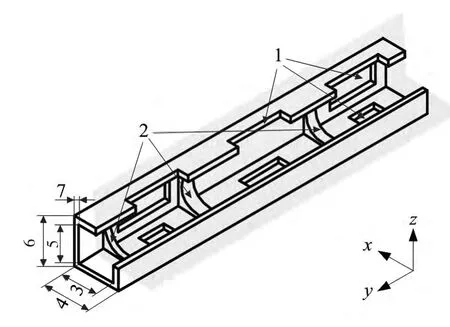
图1 方滑枕的主要结构特征及基本尺寸

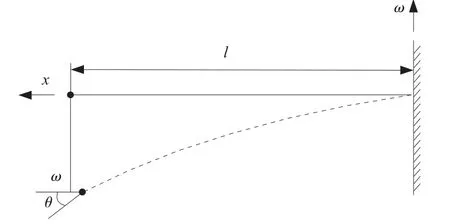
图2 滑枕的悬臂梁模型示意图

1.2 基于结构特征效应的截面惯性矩

截面惯性矩是指各微元截面至截面上某一指定轴线距离二次方与各微元面积乘积的积分，它是衡量截面抗弯能力的几何参数，其数学表达为

通常将滑枕截面视为空心等截面，进而利用式(1)进行求解。

然而滑枕上的结构特征，如形状开口、加强筋及二者的组合，使其部分等截面转化为变截面，从而使轴向各截面惯性矩呈非线性式地不等关系，进而对滑枕挠度模型的构建产生影响。就宏观角度而言，形状开口使截面实体面积减小导致其负相关于截面惯性矩;而加强筋使截面实体面积增大，故其正相关于截面惯性矩;此即结构特征对截面惯性矩的相关效应。若对各截面沿轴向进行分段从而依次计算，虽可得到精确解但求解工作量及难度都较大，且会为后续的挠度曲线方程求解过程带来诸多不便，故不宜取之。

目前在滑枕挠度误差模型构建过程中关于该结构特征效应的考虑尚未见报道，故本文以结构特征为基础，提出“结构特征正效应系数(Positive Effect Coefficient of Structural Characteristics，以下用sp表示)”和“结构特征负效应系数(Negative Effect Coefficient of Structural Characteristics，以下用sn表示)”的概念，并将这两项系数引入截面惯性矩的计算中以减小结构特征效应下截面惯性矩的求解工作量及难度。

据截面特征几何参数角度而言，加强筋是在原截面的基础上沿径向增加了新的截面面积ΔSp，且该面积在轴向上呈非线性分布(通常为分段分布);瞬时空间状态下对ΔSp沿轴向在滑枕的有效悬伸长度lx范围内积分可得加强筋有效体积ΔVp，该体积与滑枕有效悬伸体积Vx的比值，即为结构特征正效应系数，

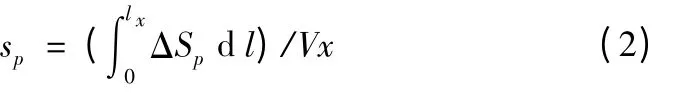
同理，形状开口在原截面的基础上沿径向减少的面积ΔSn，沿径向在有效悬伸长度lx范围内积分后得到有效负体积ΔVn，其与有效悬伸体积Vx的比值即为结构特征负效应系数，

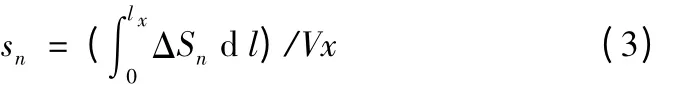
将其引入截面惯性矩的计算式后可得:

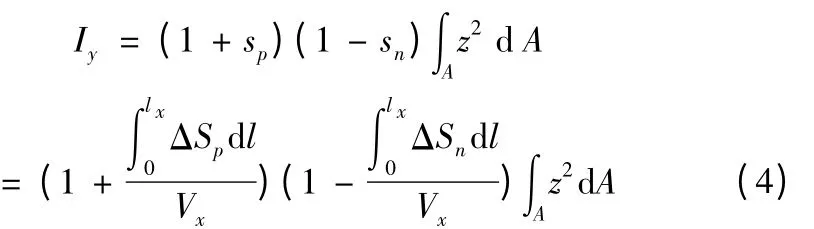
式(4)同时适用于方滑枕、圆滑枕及复合截面滑枕，仅在具体求解过程中略有不同;当滑枕的结构参数及有效悬伸长度lx确定后，即可获得Iy的值。

1.3 各类载荷条件下的综合挠度误差模型

为满足该挠度误差模型的广泛适用性，在考虑滑枕结构形式等因素的基础上，更须对其所受载荷进行分类，并获得各类载荷条件下的悬臂梁挠度信息，进一步在符合叠加原理条件的前提下进行处理，从而获得综合挠度误差曲线模型。叠加原理有两个前提条件:①材料服从胡克定律且构件是线弹性的;②位移、应变等与载荷的关系是线性的;在使用叠加原理前，须对上述两个条件进行验证。

(1)载荷分类

如图3 所示，首先据载荷大小变化将其分为定常、线性及非线性载荷;其次视载荷形式将定常载荷分为定常力矩载荷及定常力载荷;进一步以载荷作用点位置为依据将定常力矩载荷分为定常梁端力矩载荷及定常梁中力矩载荷，将定常力载荷分为定常梁端力载荷、定常梁中力载荷及均布力载荷。

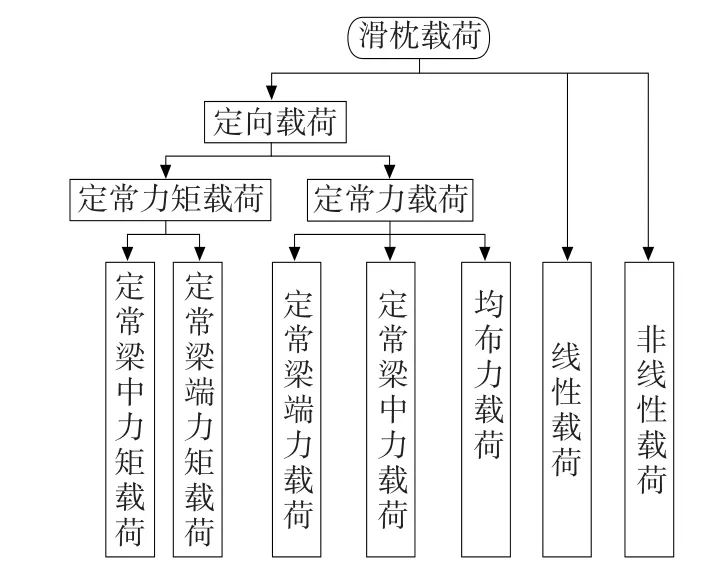
图3 滑枕的载荷分类

(2)各类载荷条件下的悬臂梁挠度信息

根据材料力学相关原理可知挠度曲线近似微分方程为

其中ω 为挠度，x为挠度参考点，M为悬臂梁所受力矩，E为弹性模量，I为截面惯性矩，可由式(4)求得。定常力及线性、非线性载荷下的悬臂梁力矩可通过理论力学相关原理求得，代入式(5)并于两边同乘dx积分后可得悬臂梁转角方程为

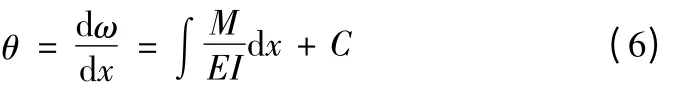
再次同乘dx积分后可得挠度曲线方程

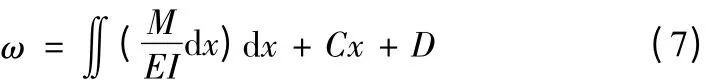
其中C、D 为积分常数，可通过悬臂梁的边界条件确定。式(5)～(7)的求解过程因载荷类型不同而略有不同;其中定常梁中力矩及定常梁中力载荷的弯矩为分段函数，故其挠度曲线方程亦分段表达。

特别指出的是:①线性载荷在式(6)、(7)的积分过程完成后必出现力载荷的平方及立方项，故线性载荷与挠度呈非线性关系，此时不满足叠加原理的前提条件;②非线性载荷的种类较多、性质复杂，可使式(6)、(7)的积分过程极为困难或不可积，且积分过程完成后也难以与挠度呈线性关系，从而不能保证叠加原理的前提条件成立;故在悬臂梁挠度信息的研究中排除上述两种载荷，定常载荷的形式简图如图4 所示。

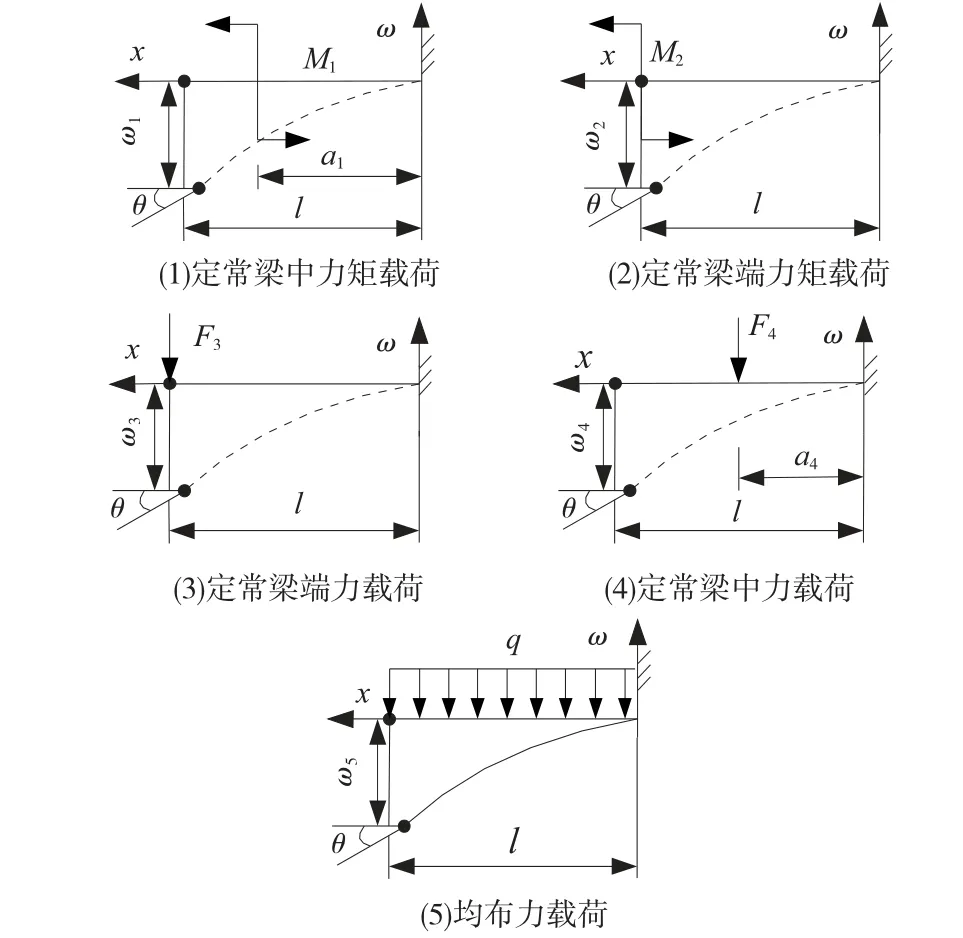
图4 定常载荷的形式简图

定常梁中力矩载荷的挠度曲线方程为

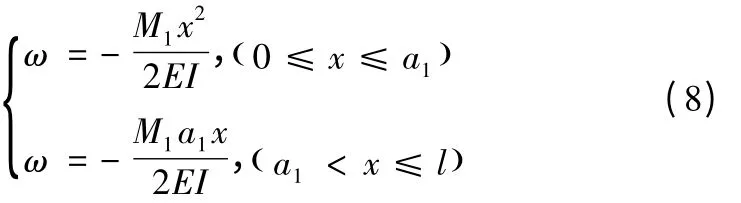
定常梁端力矩载荷的挠度曲线方程为

定常梁端力载荷的挠度曲线方程为

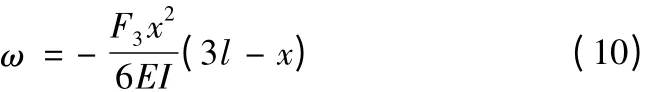
定常梁中力载荷的挠度曲线方程为

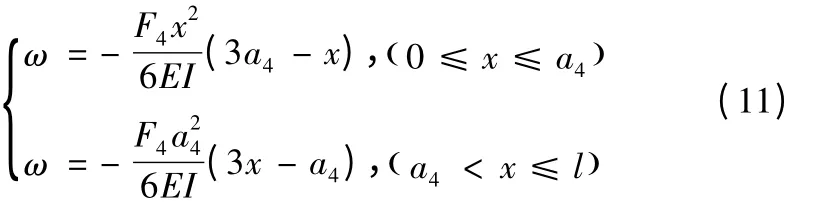
均布力载荷的挠度曲线方程为

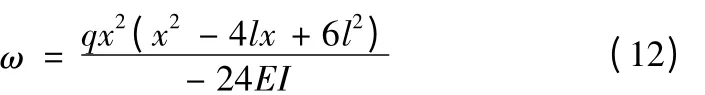
(3)各类载荷条件下的综合挠度曲线方程及梁端挠度

由式(8)～(12)可知，各项定常载荷与挠度呈线性关系，故可使用叠加原理对其进行综合;由于实际工况下的载荷为上述各项定常载荷的单类单个、单类多个或数类单个、数类多个的组合，故在利用叠加原理对挠度曲线方程进行综合时，依据“0 -1 对比评分法”对其进行加权处理后可得

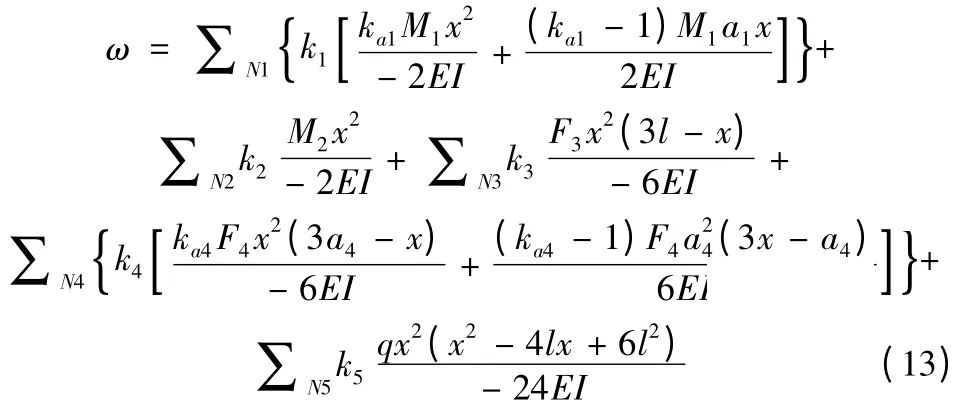
此即瞬时空间状态中各类载荷条件下的综合挠度曲线方程;当组合载荷中包含第i(i=1，2，3，4，5)项载荷时，ki取1，反之取0;Ni表示第i项载荷的数量;加权系数ka1和ka4分别满足

然而，式(13)是对悬臂梁上选定参考点的挠度评价，在实际工况下则以悬臂梁端部(也即滑枕头部)作为最佳挠度参考点，此时x=l，代入式(13)得瞬时空间状态中各类载荷条件下的悬臂梁端挠度

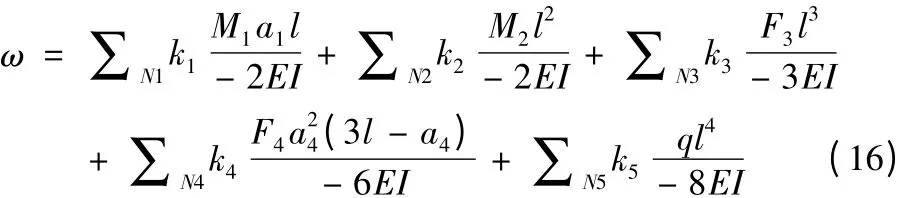
1.4 融入连续性、位变性的滑枕挠度误差预估模型

式(16)以悬臂梁为表征基体，通常视其截面为等截面、截面惯性矩I为定值;为提高梁端挠度方程精度，考虑滑枕结构特征，将式(4)引入式(16)得

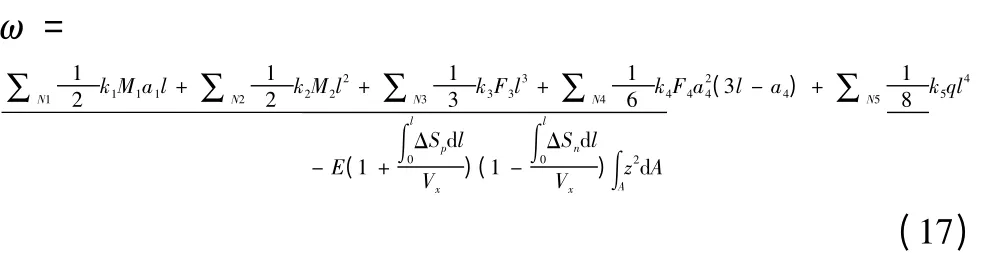
此即基于结构特征效应的滑枕头部综合挠度方程。

式(17)中l为滑枕悬伸长度，在悬臂梁模型分析过程中视其固定端为定点，而在实际工况下，该固定端的位置随着滑枕行程的变化而产生广义的位置变化，进而引起滑枕头部挠度值的变化，此即滑枕挠度的位变性表征;同时，滑枕行程在某道工序过程中不断变化使其挠度值亦不断变化，此即滑枕挠度的连续性表征;因此，为更贴合实际工况，须将该连续位变性融入式(17)。

由图4 中的载荷形式简图可知，当滑枕固定端广义位置连续变化时，滑枕悬伸长度l、定常梁中力矩载荷与固定端距离a1及定常梁中力载荷与固定端距离a4随之发生连续性变化，且三者在滑枕行程y=0mm时达到最小分别为l0、l1、l4，故有

代入式(17)后得

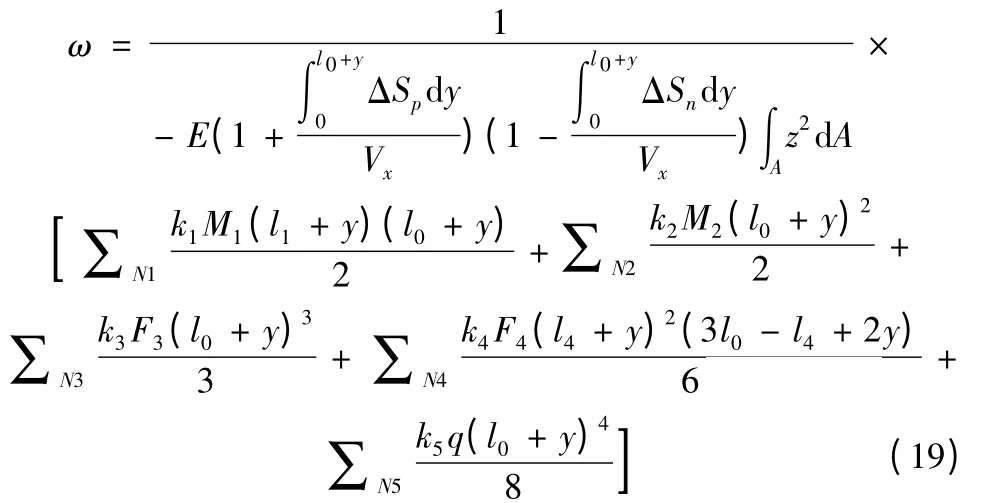
此即基于位变性及结构特征效应的滑枕挠度误差预估表达式;若令第i类载荷条件下j个子载荷的综合挠度为∑jωij(y)，则式(19)可简记为

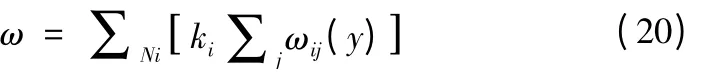
2 工程实例验证

为验证上述挠度误差预估模型的有效性，本文以TX1600G 镗铣加工中心的滑枕结构模型为实例对象、以前期文献的挠度结果为参考，通过式(19)获得该滑枕模型的挠度预估结果，并进一步与文献结果作对比分析。

2.1 滑枕模型

如图5 所示，TX1600G 镗铣加工中心滑枕采用方形结构，其端面内壁尺寸214mm × 205mm，总长2540mm，Y轴方向行程1200mm;材料使用灰铸铁HT300，弹性模量E=157GPa，自身重力4300N。

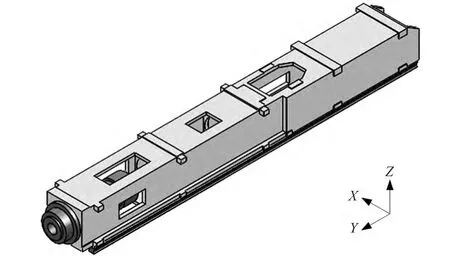
图5 TX1600G 镗铣加工中心滑枕模型

位于滑枕端部的电主轴重力为1150N，滑枕附属部件的总重力为1540N;当滑枕位于0mm 行程位置时，其端部参考点距离悬臂固定端365mm，电主轴重心、附属部件的重心距离悬臂固定端分别为245mm、

-920mm。

2.2 文献的挠度结果

文献［3］以上述滑枕模型为研究对象，考虑到其整体模型上各点的挠度值在全行程范围内呈“大数据［13］”性，故以电主轴模型头部端面中心点为基准、沿Y轴方向间隔100mm 行程为依次取点，所获得滑枕挠度结果如表1 所示。

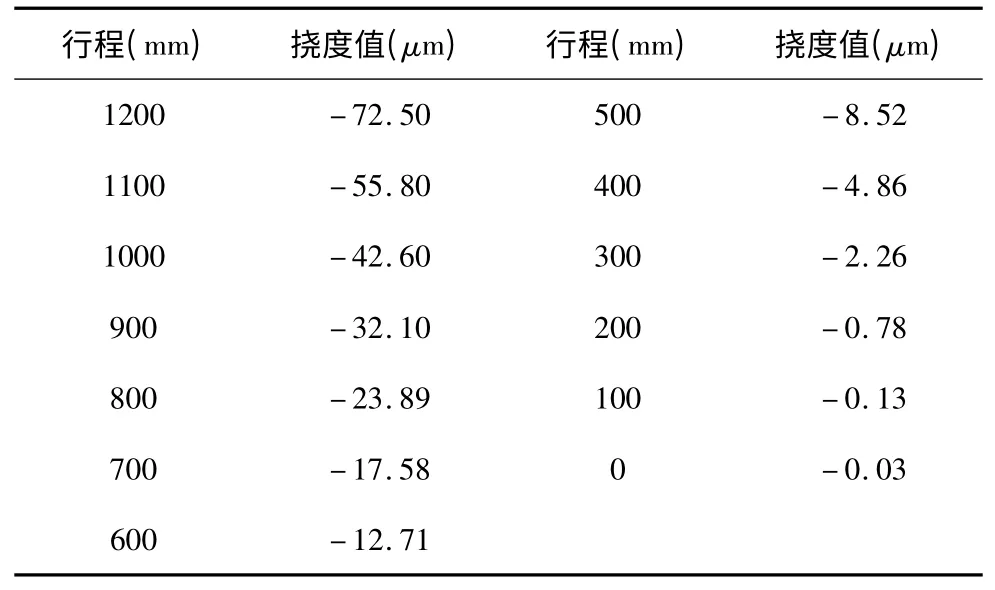
表1 文献的挠度结果

2.3 基于位变性及结构特征效应的预估挠度结果

结合滑枕模型、依据表1 可知:式(19)中ki的取值依次为k1=0、k2=0、k3=0、k4=1、k5=1 且l0=365mm;当k4=1 时，F4a=1150N，l4a=245mm，F4b=1540N，l4b= -920mm;当k5=1 时，q=1.693N/mm。

该滑枕模型的截面较为复杂，故对其沿Z向分层后进行分段积分求和;而结构特征正、负效应系数由滑枕行程、形状开口尺寸及位置、加强筋尺寸及位置等共同决定;基于上述结构特征效应的结构特征正、负效应系数sp、sn及截面惯性矩Iy的结果如表2 所示。

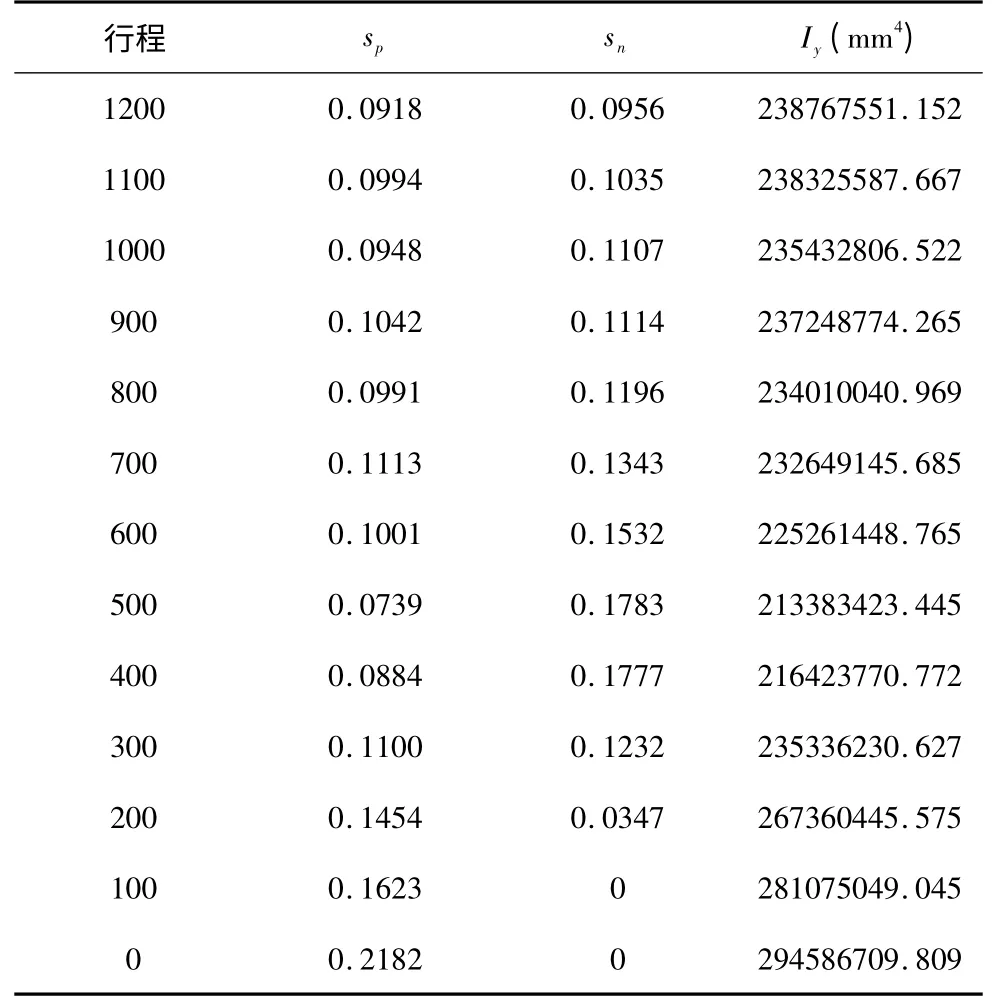
表2 sp、sn 及Iy 的值

将相关数据代入式(19)后即可得滑枕挠度的间隔预估结果，如表3 所示。

2.4 结果对比分析

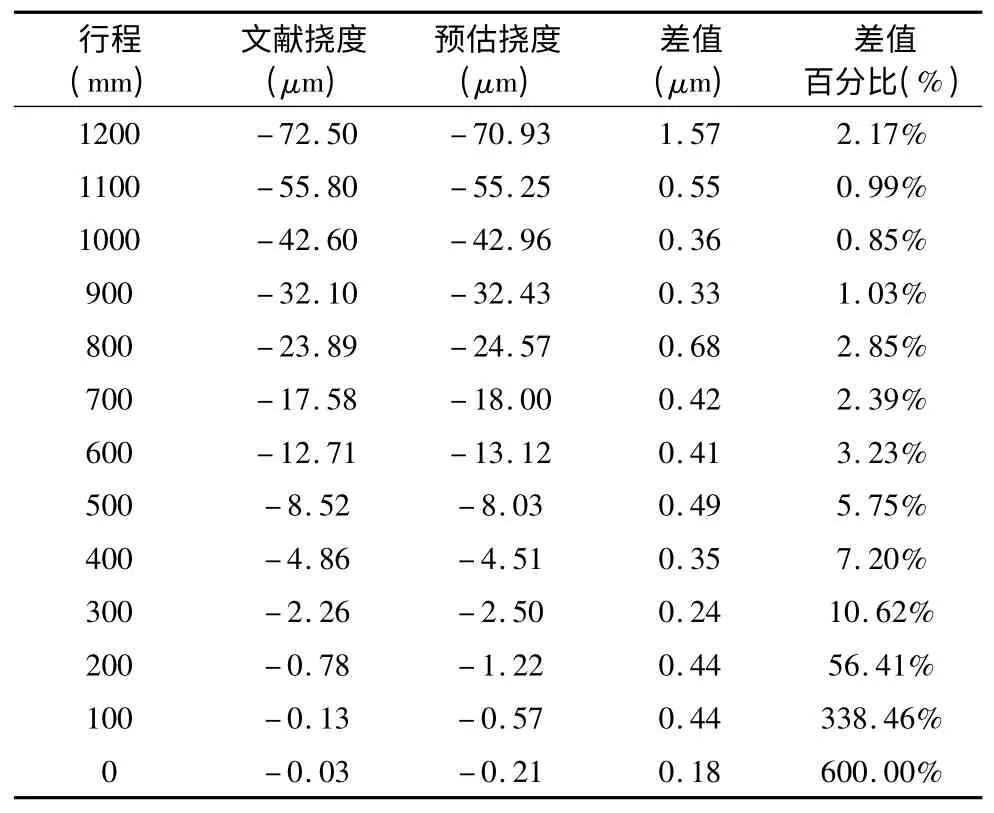
表3 文献挠度与预估挠度的对比情况

表3 中各间隔行程的预估挠度信息表明，滑枕挠度随其行程的线性增加而非线性地增大，从而再次验证了滑枕行程与其挠度误差的非线性、正相关关系。

据表3 中各间隔行程的差值可知:两种模型在1200mm 行程处的滑枕挠度差值为1.57μm，其余各行程间隔点的滑枕挠度差值均在0.7μm 内，故就差值情况而言，该挠度预估模型具有良好的数值精度。

表3 中的差值百分比以文献挠度作为标准基数。滑枕位于600～1200mm 行程内时，两种模型的挠度差值百分比均在5%以内，故此行程段内该挠度预估模型具有良好的准确度;当滑枕位于400mm、500mm 行程处时，差值百分比分别为4. 75%、7. 20%，均小于10%，故该行程处此模型的挠度误差预估效果较好。

当滑枕位于300mm 及以下行程时，差值百分比均大于10%，其中在200mm、100mm、0mm 行程处的差值百分比为338.46%、600.00%，原因有二:①此行程处的文献挠度值较小，导致差值百分比的基数过小，同时导致同等数值精度下其百分比过大，从而使得其置信度降低;②结合滑枕结构(图5)及表2 中sn的数值变化可知，悬伸部分的形状开口及加强筋等结构特征，使得该结构区域内的滑枕重力在Y轴方向呈可线性处理的弱非线性分布，但该滑枕结构短行程内悬伸部分的形状开口数量及面积都较大，使其在短行程的局部范围内重力呈类阶跃式的较强非线性，从而对差值百分比产生较大的影响。基于上述原因的综合影响，使得短行程范围内的差值百分比置信度降低，难以作为参考数据来衡量挠度预估结果;其次，相对长行程处的挠度而言，短行程处的挠度与之存在数量级的差距，且该差距并不会因结构特征对滑枕重力分布的非线性影响而具逾越之势，进而致使短行程内挠度值的参考价值较低;再次，该挠度预估模型在差值的数值精度上具有极佳的表征性，且中、长行程范围的差值百分比亦有良好的预估效果。

综上可知，本文提出的滑枕挠度预估模型是有效合理的。

3 结论

(1)本文以滑枕设计模型为基础分析了结构特征对截面惯性矩的影响效应，首次提出并定义了结构特征正、负效应系数的的概念，并将这两项系数引入截面惯性矩的传统公式中，获得了基于结构特征效应的截面惯性矩修正计算式，更加贴切地反映了结构的截面抗弯能力。

(2)以广泛适用性为出发点，基于叠加原理、悬臂梁假设等理论，引入截面惯性矩的修正计算式，在瞬时空间内获得了各类载荷条件下的综合挠度曲线模型;进一步融入连续性、位变性后导出滑枕挠度误差的预估模型，并通过工程实例验证了该预估模型的有效性。

(3)本文提出的基于位变性及结构特征效应的滑枕挠度误差预估模型，为工程技术人员在图纸及方案设计阶段对滑枕挠度的预测提供了量化依据，同时对滑枕结构的优化设计、补偿等具有指导意义，从而为机床同类问题的解决提供了有效的途径。

［1］高峰，郭为忠，宋清玉，等. 重型制造装备国内外研究与发展［J］. 机械工程学报，2010，46 (19):92 -107.

［2］刘海涛，赵万华. 基于广义加工空间概念的机床动态特性分析［J］. 机械工程学报，2010，46 (21):54 -60.

［3］康俊贤，王军，刘傲翔，等. TX1600G 镗铣加工中心滑枕挠度分析与补偿方法研究［J］. 组合机床与自动化加工技术，2014(8):12 -17.

［4］WU F，QIAO L，XU Y. Deformation Compensation of Ram Components of Super-heavy-duty CNC Floor Type Boring and Milling Machine ［J］. Chinese Journal of Aeronautics，2012，25(2):269 -275.

［5］Vondrák P. The design of plate horizontal boring mill［D］.CZE:Brno University of Technology，2013.

［6］吴凤和，赵峰兵. 拉杆与推杆组合式滑枕挠曲变形补偿法［J］. 中国机械工程，2012，23(22):2667 -2670.

［7］周震东，王金娥. TH6918 滑枕变形分析及补偿方法［J］. 机械设计与制造，2013 (5):201 -203.

［8］Schwenke H，Knapp W，Haitjema H，et al. Geometric error measurement and compensation of machines—an update［J］. CIRP Annals-Manufacturing Technology，2008，57(2):660-675.

［9］de Lacalle L N L，Lamikiz A. Machine tools for high performance machining［M］. Springer，2009.

［10］Rahman M，Heikkala J，Lappalainen K. Modeling，measurement and error compensation of multi-axis machine tools.Part I:theory［J］. International Journal of Machine Tools and Manufacture，2000，40(10):1535 -1546.

［11］胡汝凯，黄美发，张奎奎，等. 数控龙门铣床滑枕的动态特性分析及改进［J］. 组合机床与自动化加工技术，2014(5):43 -45.

［12］刘傲翔，王军，康俊贤，等. TX1600G 镗铣加工中心龙门铣削系统动态特性分析［J］. 组合机床与自动化加工技术，2014(5):50 -53.

［13］Mattmann C A. Computing:A vision for data science［J］.Nature，2013，493(7433):473 -475.