柔性S 型加减速控制算法研究*

刘 筱，吴文江，郑飂默

(1.中国科学院 研究生院，北京 100049;2.中国科学院 沈阳计算技术研究所，沈阳 110168;3.沈阳高精数控技术有限公司，沈阳 110168)

0 引言

加减速控制是开放式数控系统开发的关键技术之一［4］。目前国内外学者就速度规划问题展开了一系列的研究。文献［4］提出了一种七段S 型加减速控制算法，但是算法实现较为复杂。文献［5］在七段S 型控制算法的基础上，将算法进行简化，提出了五段S 型加减速控制算法，但在加减速过程中存在初速度和末速度相等的限制。文献［6］通过选取初速度和末速度，计算出加速区、匀速区和减速区的时间长度，消除了一般S 型曲线加减速方法在路径加工中初速度和末速度相同的约束。

加加速度的最大值反映的是系统的柔性，取值大，则冲击大，取值小，则加减速时间长［4］。一般的S 型加减速控制算法在整个路径上的加速度和加加速度最大值都是固定的。

本文提出的柔性S 型加减速控制算法，为不同的路径设置不同的加加速度最大值。通过与相邻路径间的夹角对本路径段的最大加加速度进行调控，实现对系统的柔性控制。实验表明，该算法在保证了较高加工速度的前提下，能有效降低机床的冲击，实现柔性的系统控制。

1 五段S 型加减速算法

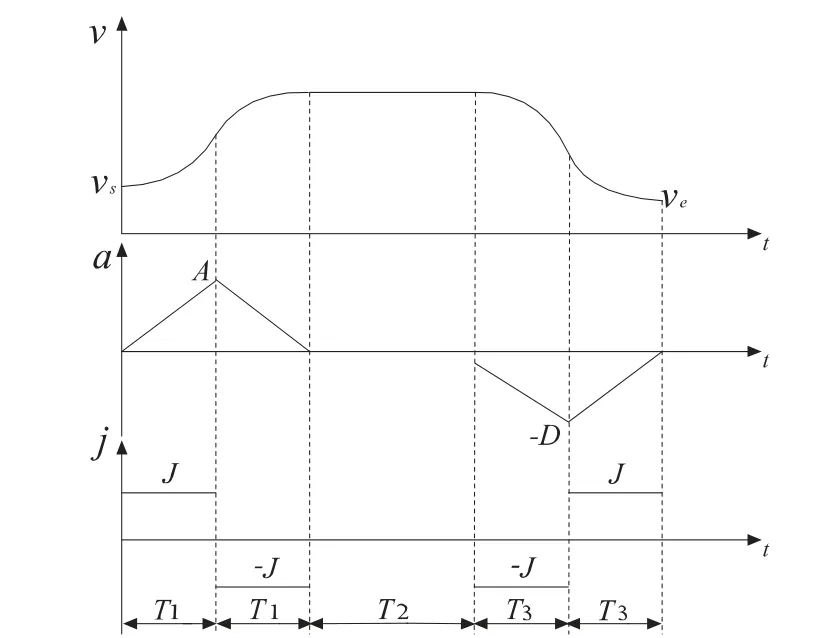
图1 五段S 型加减速

图1 为五段S 型加减速过程中速度、加速度、加加速度与时间t的关系曲线。五段S 型加减速分为加减速段、减加速段、匀速段、加减速段及减减速段。加加速和减加速的时间相等，设为T1;匀速时间设为T2;加减速和减减速的时间相等，设为T3。五段S 型加减速算法与七段相比，省略了匀加速和匀减速阶段，在不减弱速度平滑性的前提下，大大降低了计算复杂度［3］。

由加加速度、加速度、速度以及位移之间的关系，有:

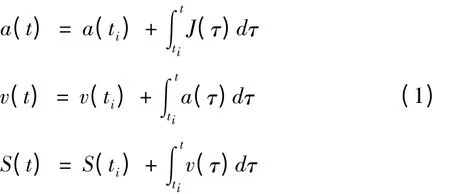
利用上式可以推到出加速度、速度、位移的计算公式分别为:

根据给定路径的长度L、加速度的最大值A、减速度的最大值D、加加速度的最大值J、初始速度Vs以及末尾速度Ve即可计算出该路径段对应的各个参数以及相应的速度曲线。

2 最大加加速度限制

传统的加减速控制算法中，加速度和加加速度的最大值都是固定的，如图1 所示。加加速度在开始时即达到最大值J，在t1时刻减为0，在t2时刻减小到负的最大值-J。在整个加减速控制的过程中，加加速度的最大值都是保持不变的。

最大加速度的值从驱动电动机的最大力矩和力极限得到，反映了系统的最大加减速能力。而最大加加速度则反映了系统的柔性，若取值较大，则冲击较大，取值小，则系统的加减速过程时间长［4］。如果想实现对系统的柔性控制，就需要对加加速度的最大值进行合理的调控。

本文提出一种思想，加加速度的最大值不再固定不变，而是在速度规划过程中随着路径不同而动态变化。具体表现就是，某段路径上加加速度的最大值跟与之相邻路径间的夹角相关。

为了满足高速高精的加工需求，应尽量保证相邻路径间速度的平滑过渡。如图2 所示:若相邻两段路径间的夹角较小，则刀具可以在较高的速度下实现平滑走刀，此时设置较小的加加速度值，即可将速度降低到指定的速度，同时保证了系统的柔性控制;若相邻两段路径间的夹角较大，速度必然需要降到一个较小的值才能实现平滑过渡，此时将加加速度设置为较大的值，则减速时间明显降低，达到高速的加工需求。

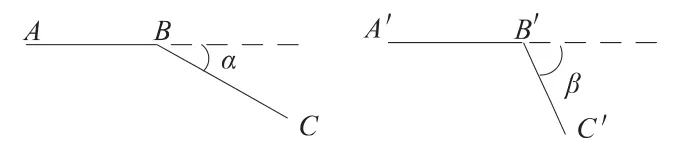
图2 相邻两段路径间夹角

本文中，加加速度最大值与路径间夹角的关系为:

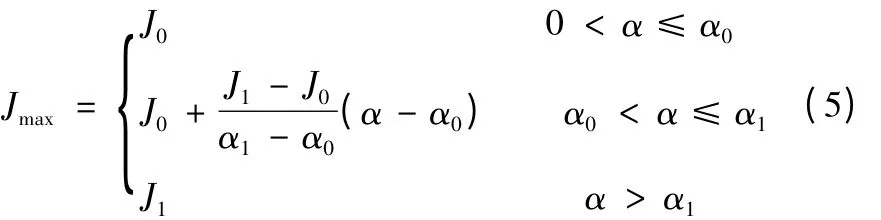
其中α 为相邻路径间的夹角，具体表现为图3 所示:

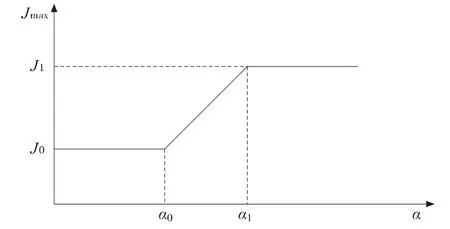
图3 加加速度与路径间夹角关系图

当相邻路径间夹角小于α0时，加加速度的最大值保持J0不变;当相邻路径间夹角大于α1时，加加速度的最大值保持J1不变;当相邻路径间夹角在α0～α1之间动态变化的时候，加加速度的最大值也在J0～J1之间线性的变化。此处，α0、α1、J0、J1都可在速度规划时进行设置，不同的加工工件可以配置不同的值。

3 柔性S 型加减速控制模型

本文提出一种柔性的S 型加减速控制模型，每个路径段单独保留最大的加加速度值，达到整体柔性控制的效果。算法流程图如图4 所示。

每次读取相邻两个路径的位置数据，计算出两段路径间的夹角，根据最大加加速度限制的思想求出本路径的加加速度最大值，然后带入五段S型加减速控制模型中计算出加速区、匀速区及减速区的时间长度。至此，整个加工轨迹的速度规划完成。

图4 柔性S 型加减速规划算法流程图

4 示例

本文取三段路径进行说明，起点为(0，0)，分别经过(30，15)、(60，15)到达终点(80，35)。轨迹图如图5所示:

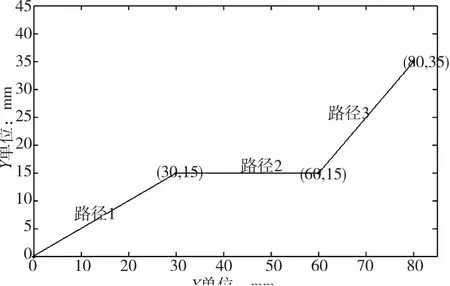
图5 加工轨迹图

设置最大加速度限制参数如下:

则加加速度最大值与夹角的关系可具体化为:

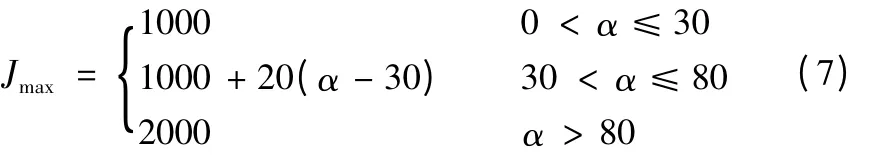
根据本文提出的柔性S 型加减速规划算法，首先计算相邻路径间的夹角，可得α1= 26.5651°、α2=45.0°。由于路径3 为本例中最后一段路径，故不进行角度计算。据此可求得各路径段的加速度最大值分别为:

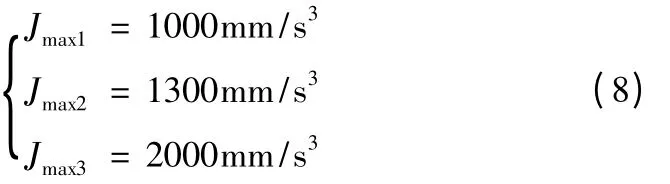
按五段S 型加减速控制算法即可求得各路径的速度、加速度以及位移轨迹。

以路径1 为例，设vmax=50mm/s，vs=0mm/s，ve=10mm/s，又根据式(8)Jmax1=1000mm/s3。求得T1=0.2236s、T2=0.2072s、T3=0.20s。路径2 与路径3 亦可以同样的方式求得。整个加工轨迹的数据如表1 所示:

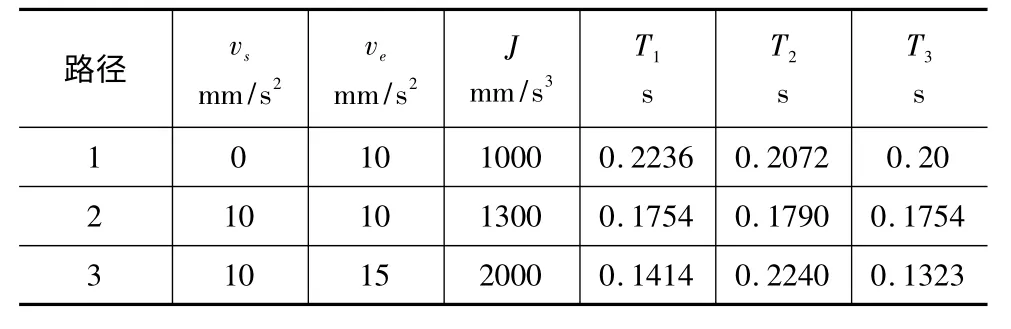
表1 路径轨迹规则

整个加工轨迹的速度曲线如图6 所示，蓝色曲线代表本文提出的柔性加减速控制模型;红色曲线代表普通五段S 型曲线加减速控制模型。

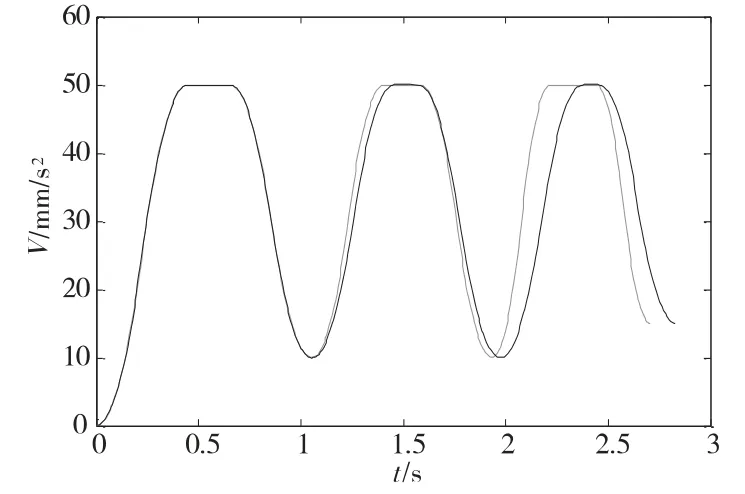
图6 加工轨迹速度曲线

本文提出的算法运行时间为2.7064s，小于五段S型加减速控制算法所得的运行时间2.8301s。在蓝色曲线中，由于路径2 与路径3 的加加速度最大值不同，速度由相同的值增加到最大值用的时间也不同。由图6 可以看出，蓝色曲线的光滑性并没有降低，证明了本文算法在提高效率的前提下，能够实现系统的柔性控制。

5 结论

本文提出的柔性S 型加减速控制算法是基于五段S 型加减速控制算法，并在此基础上提出了各路径段加加速度最大值不同的思想。通过相邻路径之间的夹角对路径的加加速度最大值进行控制，然后根据五段S 型算法思想计算各路径段的参数。实验结果显示，在整体的轨迹规划过程中，本文提出的算法能够做到高速度与低冲击率的结合，大大提高加工效率。

［1］Zhang K，Yuan C M，Gao X S，et al. A greedy algorithm for feedrate planning of CNC machines along curved tool paths with confined jerk［J］. Robotics and Computer-Integrated Manufacturing，2012，28(4):472 -483.

［2］Timar S D，Farouki R T. WITHDRAWN:Time-optimal traversal of curved paths by Cartesian CNC machines under both constant and speed-dependent axis acceleration bounds［J］.Robotics and Computer-Integrated Manufacturing，2008，24(1):16 -31.

［3］Timar S D，Farouki R T，Smith T S，et al. Algorithms for time-optimal control of CNC machines along curved tool paths［J］. Robotics and Computer-Integrated Manufacturing，2005，21(1):37 -53.

［4］黄艳，李家霁，于东，等. CNC 系统S 型曲线加减速算法的设计与实现［J］. 制造技术与机床，2005(3):59 -63

［5］李晓辉，邬义杰，冷洪滨. S 曲线加减速控制新方法的研究［J］. 组合机床与自动化加工技术，2007(10):50 -53.

［6］冷洪滨，邬义杰，潘晓弘. 三次多项式型微段高速加工速度规划算法研究［J］. 计算机集成制造系统，2008(2):336 -340，397.

［7］盖荣丽，林浒，郑飂默. 高速加工中速度规划算法的研究与实现［J］. 小型微型计算机系统，2009，30 (6):1067 -1071.

［8］赵巍，王太勇，万淑敏. 基于NURBS 曲线的加减速控制方法研究［J］. 中国机械工程，2006，17(1):1 -3.

［9］胡磊，林示麟，徐建明，等. S 曲线加减速速度控制新方法［J］. 组合机床与自动化加工技术，2010(1):22 -26，34.

［10］付进伟，董辉，王建军. 连续小直线段速度控制算法研究［J］. 机械设计与制造，2012(6):9 -11.