偏航减速器行星传动系统静力学均载特性研究

吴一凡，张锁怀

(1.陕西科技大学 机电工程学院，西安 710021;2. 上海应用技术学院 机械工程学院，上海201418)

0 引言

行星齿轮传动系统中采用数个完全相同的行星齿轮共同承担载荷，形成功率分流，使其与普通齿轮系相比具有重量轻、体积小、传递功率大，承载能力强和传动平稳等优点。然而在齿轮生产、装配等过程中不可避免地会产生制造、安装误差，且齿轮在高速运转时，由于发热变形和受惯性力、摩擦力等作用产生变形，使行星齿轮机构中各行星轮所受实际载荷无法实现完全均匀分配。如果各行星轮间载荷分配不均衡，不但行星齿轮传动的优点难以实现，而且会使系统的噪声增大，影响机构运转的平稳性和可靠性，使减速器的性能和使用寿命受到严重影响。因此，深入研究行星齿轮传动的均载特性，对提高行星齿轮传动系统的性能具有重要的意义。

日本学者日高照晃、杉本信行［1］等运用静力学方法，研究了行星齿轮装置均载机构中各类误差与载荷分配的关系，并指出浮动基本构件可以降低误差对行星轮不均载的影响。20 世纪90 年代初，美国国家航空航天局开展了行星齿轮传动系统均载性能的研究工作［2-4］。1994 年，Kahraman［5］先后对行星齿轮传动装置从静态力学和动态力学两个角度作了力学分析，并在此基础上给出了静态均载系数、动态均载系数和动态系数的定义，最后用实验论证了所建立的模型的正确性，为研究行星齿轮传动的均载效果提供了科学的方法。国内方面，肖铁英［6］等人通过研究均载机理为均载系数的计算提供了公式和方法。陆俊华、李斌和朱如鹏［7］等建立了2K-H 型行星齿轮传动系统静力学均载系数计算模型，指出系统的均载系数是各误差综合作用的结果，如果只注意其中某一项误差并不能使系统的均载情况得到良好的改善。也有一些学者从其他方面研究行星齿轮传动系统静力学均载特性［8-11］，这些研究主要是以单级行星齿轮传动系统为研究对象，且分析齿轮误差对系统均载的影响时侧重点各有不同。

本文以偏航减速器四级行星齿轮传动系统为研究对象，建立2K-H 型行星齿轮传动系统的静力学分析模型，基于当量啮合误差原理，推导当量啮合误差计算公式和行星齿轮系统均载系数计算公式，并通过Matlab 编程计算得到各级传动的均载系数，分析制造、安装误差对行星传动系统均载的影响以及各行星轮出现均载不理想时的相位。

1 物理模型

采用由刚体和弹簧组成的集中质量模型建立如图1 所示的单级行星齿轮传动系统静力学均载分析模型，将各齿轮和行星架视为刚体，太阳轮或行星架为基本浮动构件，用等效弹簧表示回转副、各支撑和齿轮啮合处的弹性变形。Kspj为由太阳轮和行星轮组成的外啮合副的等效啮合刚度，Krpj为由行星轮和内齿轮组成的内啮合副的等效啮合刚度;Ks、Kp、Kc分别为太阳轮、行星轮和行星架的等效平移支撑刚度;Ksθ、Kpθ、Kcθ分别为太阳轮、行星轮和内齿轮的回转支撑刚度。

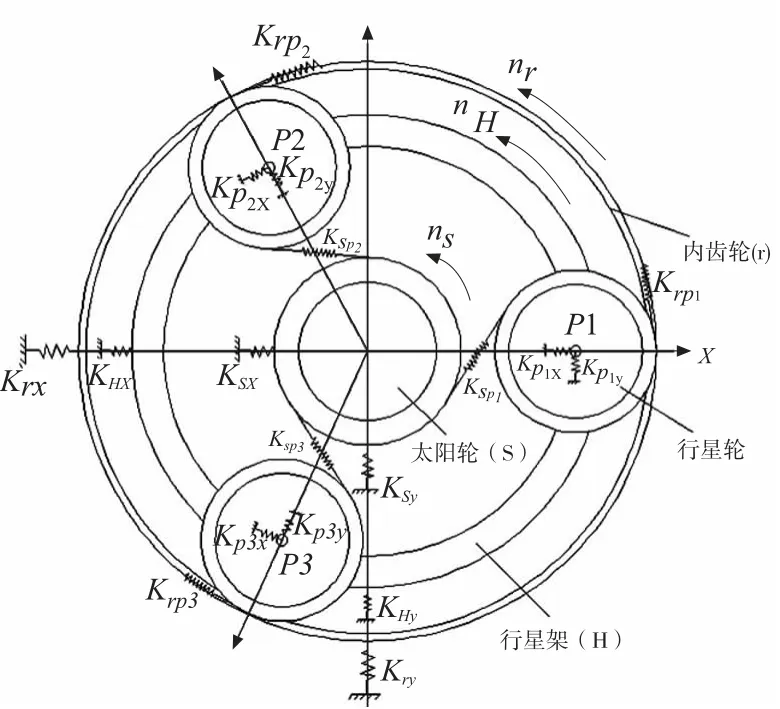
图1 NGW 型行星齿轮传动系统物理模型

该模型中各构件都具有一个转动和两个平动共三个自由度，分别为:太阳轮轮θs、xs、ys;行星轮θpj、ξpj、ηpj;行星架θc、xc、yc;内齿轮θr、xr、yr。

2 传动系统的等效误差

在行星齿轮传动系统中，通常认为综合啮合误差由两部分误差组成，一部分为累积啮合误差，它主要由构件的制造、安装误差引起;另一部分为浮动啮合误差，它由浮动构件的中心位移引起［5］。累积啮合误差主要包括太阳轮、行星轮、行星架和内齿轮的制造偏心误差和安装误差;浮动啮合误差主要包括太阳轮浮动、行星架浮动引起的啮合侧隙。为了便于分析各误差的大小和方向，以E、A分别表示制造误差和安装误差的大小，这两种误差的方向分别以β、γ 表示，s、pj、c、r为下角标，分别对应太阳轮、第j个行星轮、行星架和内齿圈。αw、αn分别表示行星齿轮传动中外啮合与内啮合的啮合角。

2.1 当量啮合误差

为了便于分析制造误差和安装误差对行星齿轮间载荷分布的影响，将各误差沿相应的内、外啮合线方向进行分解，这种啮合线方向上经分解得到的误差就称为当量啮合误差。取当量啮合误差离开啮合线的方向为正。

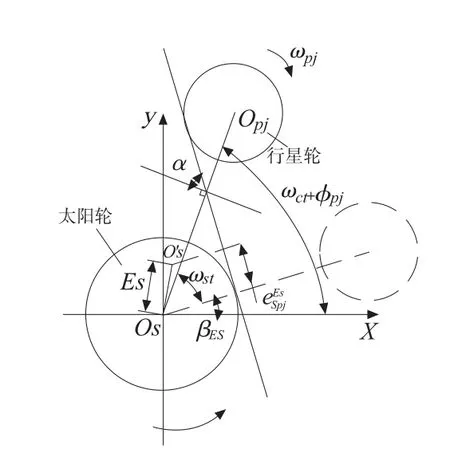
图2 误差沿外啮合线当量化模型

以太阳轮制造偏心误差的当量化计算为例，推导各制造误差沿外啮合线的当量化公式，不妨设太阳轮逆时针转动的方向为正方向。分析图2 中的角度关系可知，t时刻太阳轮制造偏心误差Es的方向与外啮合线的夹角ηEs为

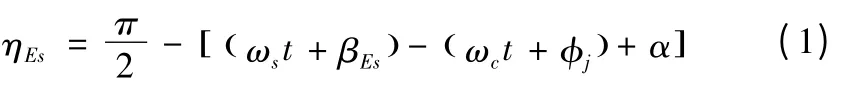
式中，ωs、ωc分别表示太阳轮与行星架的转速;φj表示第j个行星轮的位置角，假设第一个行星轮的中心位于x轴上，则第j个行星轮位置角的计算公式为

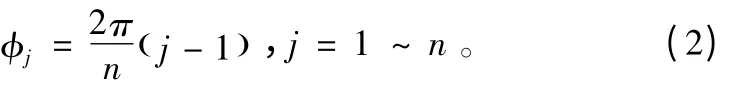
于是，太阳轮制造偏心误差沿外啮合线方向的当量啮合误差为

整理可得出由太阳轮制造误差Es所引起的当量啮合误差为，其中，βEs为太阳轮制造误差的方位角。

同理，可以计算其他各构件因制造和安装误差和当量啮合误差

太阳轮外啮合当量啮合误差:

行星轮外啮合当量啮合误差:

行星轮内啮合当量啮合误差:

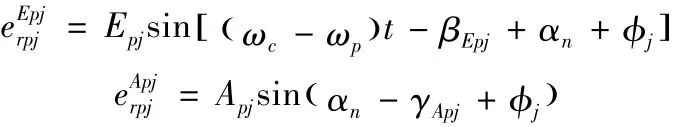
内齿轮内啮合当量啮合误差:

行星架外啮合当量啮合误差:

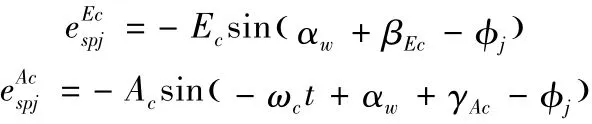
行星架内啮合当量啮合误差;

在上述计算当量啮合误差的公式中，ωs、ωc、ωp分别为太阳轮、行星架、行星轮的角速度;t为时间;φj为第j个行星轮相对于第一个行星轮的位置角。

累积啮合误差就是啮合线上所有制造、安装误差的叠加，于是外、内啮合线上的累积啮合误差分别为

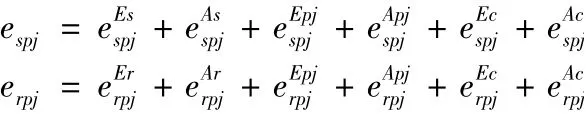
2.2 浮动误差

由浮动构件中心位移引起的侧隙是综合啮合误差的另一个重要组成部分，把这一误差称为浮动误差，其大小由构件中心位移量决定。文中假设太阳轮为基本浮动构件，推导太阳轮的中心位移在相应啮合线方向上的位移量计算公式，其分析模型如图3 所示。设太阳轮中心在x，y方向的位移分别为xs与ys，Wj为t时刻太阳轮与第j个行星轮在外啮合线上的方位角，Nj为t时刻内齿圈与第j个行星轮在内啮合线上的方位角。

因为内齿轮固定，故以内齿轮的中心o为原点，水平方向为x轴，竖直方向为y轴建立直角坐标系。假设太阳轮中心由于浮动运动到位置o＇，则在t时刻太阳轮中心沿x方向的位移与啮合线的夹角Wj为:

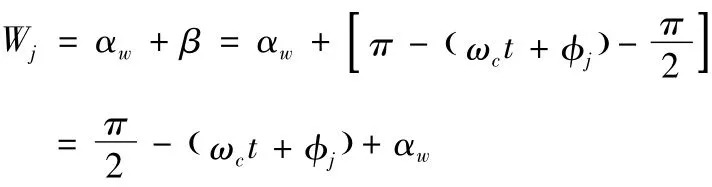
则太阳轮中心位移xs、ys沿外啮合线方向的位移为:

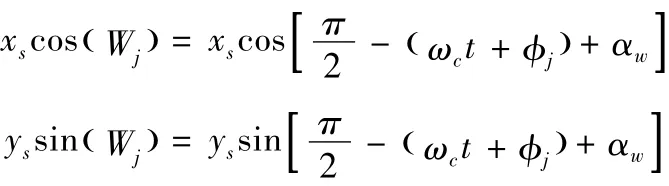
此时太阳轮中心浮动位移xs与ys的当量啮合误差为:

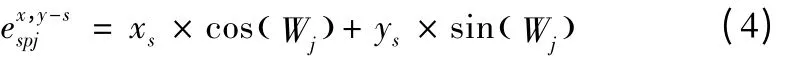
同理可得，如果行星架中心在x，y方向的位移量为xc与yc，则行星架浮动时其中心位移在外、内啮合线上引起的等效误差分别为:

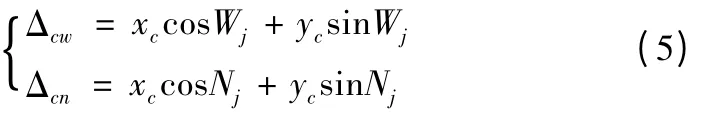
式中，t时刻内齿轮与第j个行星轮在内啮合线上的方位角

将累积啮合误差和浮动误差叠加，即得太阳轮浮动时外、内啮合线上的综合误差为:

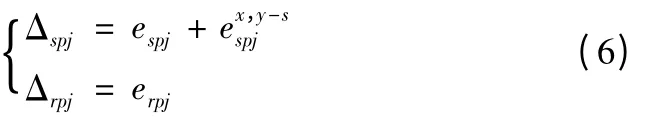
同理，可以推导行星架浮动时，外、内啮合线上的综合啮合误差为:

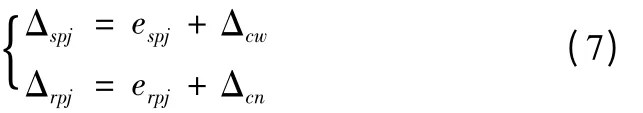
3 均载系数计算

在啮合副和齿轮支撑系统弹性变形的作用下太阳轮和行星轮的中心会产生平动位移和转动位移，最终使齿轮间的啮合侧隙完全消除，设由变形引起的太阳轮和第j个行星轮的微转角分别为θs和θpj，则太阳轮和第j个行星轮间的作用力Fspj与内齿轮和第j个行星轮间的作用力Frpj分别为:

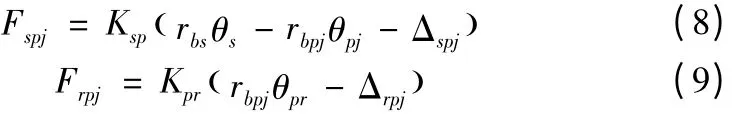
其中，rbs、rbpj分别为太阳轮、行星轮基圆半径;Ksp、Kpr分别为外、内啮合等效刚度。由式(8)、(9)可得:

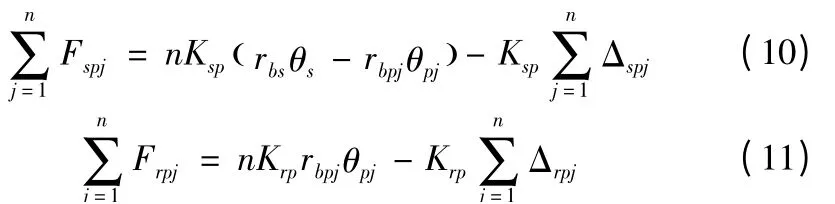
将式(10)、(11)分别代入(8)、(9)可得:

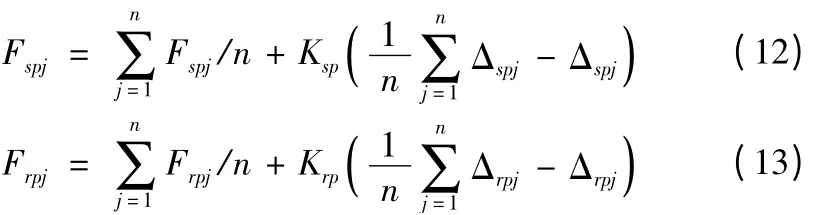
对于整个系统，太阳轮和行星轮的静力平衡方程分别为:

考虑太阳轮浮动时，则有以下平衡方程:

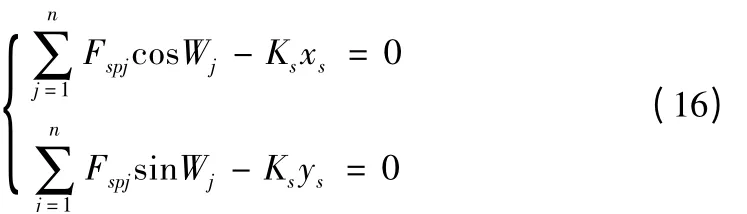
考虑行星架浮动时，则有以下平衡方程:

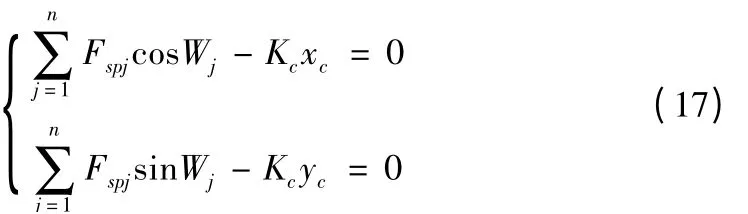
联立以上各式，便可求出Fspj和Frpj，则行星传动系统中第j个行星轮的均载系数为

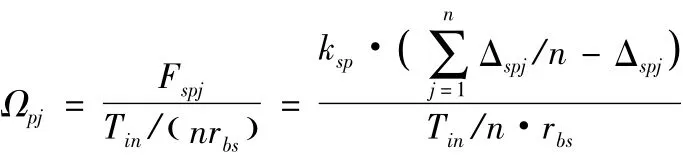
式中，Tin为第一级太阳轮所受扭矩，n为行星轮个数。

由此可得多级行星传动系统的均载系数为:

式中i代表传动的级数。

4 算例

以偏航减速器的第一级行星齿轮传动系统为例。第一级传动系统中内齿圈固定，采用行星架浮动。产品立式安装，其均载完全取决于每级三个行星齿轮的齿轮啮合力的平衡，不受重力影响。构件的各误差值均取为5 μm，各误差的初始方位角均取为0°。其主要参数如表1 所示。

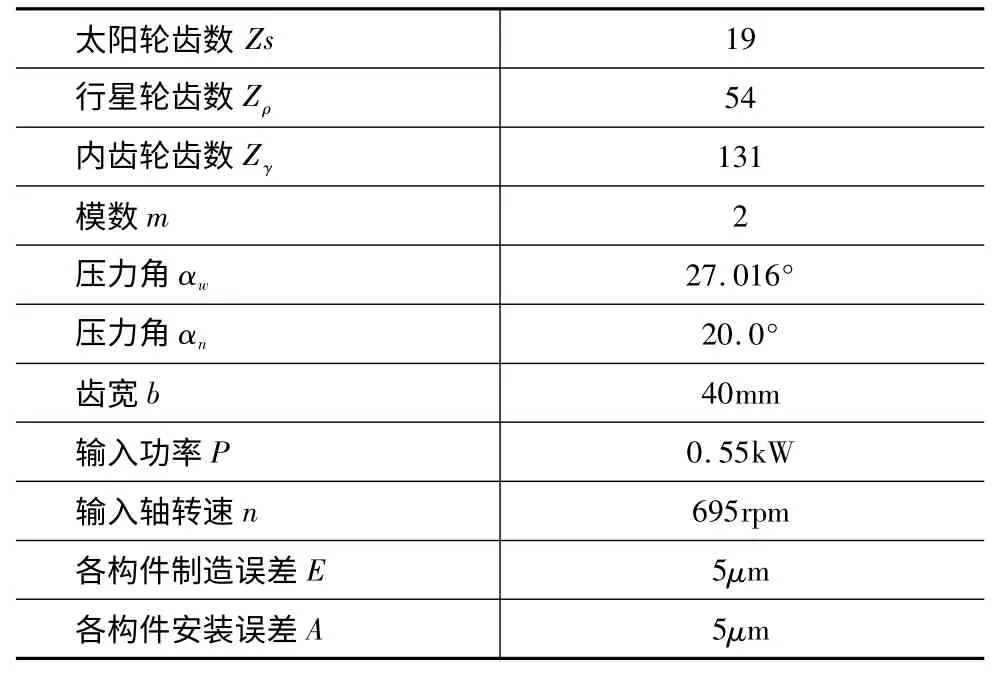
表1 第一级行星齿轮传动基本参数

4.1 误差综合作用时的均载系数

根据上述公式，通过Matlab 计算得到第一级三个行星轮的均载系数如图4 所示。

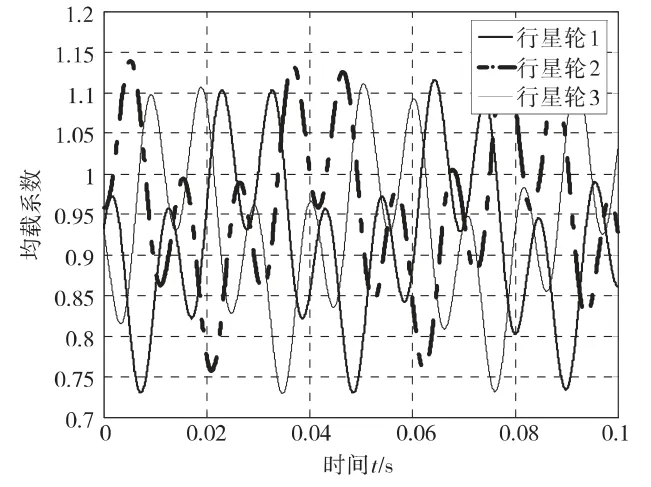
图4 各行星轮均载系数变化情况

从图中可以看出，在误差的综合作用下各行星轮的均载系数随时间按一定的周期规律变化。计算得到第一级传动系统的均载系数Ω1=1.1396 。同理可计算出偏航减速器第二、三、四级行星齿轮传动系统的均载系数分别为Ω2=1.1362 ，Ω3=1.1278 ，Ω4=1.1757 。

4.2 误差单独作用对均载系数的影响

假定其余误差值均为零，研究某一误差单独作用对行星齿轮间载荷分配均匀性的影响，结果如图5 所示。

图5 误差单独作用时的均载系数

从上图中可以看出，对于周期变化的太阳轮制造误差Es、太阳轮安装误差As、行星轮制造误差Ep和行星架安装误差Ac，各行星轮的均载系数都是周期变化的。

4.3 误差单独变化对均载系数的影响

当其余误差的大小保持一定值时，为研究某一误差单独变化对行星齿轮间载荷分配均匀性的影响，并进一步比较各误差对系统均载系数的影响程度，本文编写了相关计算程序通过Matlab 图形处理工具显示其影响规律如图6 所示。

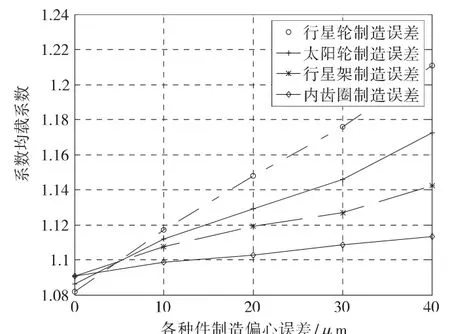
图6 各误差单独变化对均载系数的影响

从上图中可以看出，在构件的制造偏心误差中，对系统均载情况影响最大的是行星轮制造偏心误差，其次分别是太阳轮和行星架，内齿圈的制造误差影响最小;在某一误差单独变化，其它误差保持某一定值不变时，系统的均载系数随该误差的变化可近似地认为是线性的。

5 频率特性分析

通过Matlab 编程计算分别出第一级传动系统三个行星轮均载系数函数的实际幅值-频率图和相位-频率图(离散信号)，如图7 所示。从图中可知，当n=8 和n=32时(相应的频率为24.9Hz 和96.6Hz)，实际幅值较大，而其他点处的幅值可视为零;第一个行星齿轮在其相位φ1为100°和-79.5°附近，具有较大的均载系数值，第二个行星齿轮在其相位φ2为-12.5°和150°附近，具有较大的均载系数值，第三个行星齿轮在其相位φ3为-135°和35°附近，具有较大的均载系数值。

图7 行星轮均载系数的幅相频率特性

6 结论

在误差的综合作用下行星轮系的均载系数随时间按一定规律周期变化。在构件的制造偏心误差中，对系统均载情况影响最大的是行星轮制造偏心误差，其次分别是太阳轮和行星架，内齿圈的制造误差影响最小。分析行星齿轮载荷分配不均衡系数函数的幅/相频率特性，得出传动系统在不均载时各行星轮的相位。

［1］日高照晃，山本信行，石武田.行星齿轮传动装置均载机构中各误差和载荷分配的关系［C］. 日本机械学会论文集.1986，52(48):2200 -2206.

［2］Krantz T L. A method to analyze and optimize the load sharing of split path transmissions［R］.NASA Technical Memorandum 107201.1996.

［3］Krantz T L，Delgado I R. Experimental Study of Split-path Transmission Load Sharing［R］. San Diego:NASA Technical Memorandum 107202，1996:1 -9.

［4］Kish J G. Sikorsky Aircraft Advanced Rotorcraft Transmission (ART)Program-Final Report［R］. NASA CR-191079，NASA Lew is Research Center，1993:1 -77.

［5］Kahramn A. Load sharing characteristics of planetary transmissions［J］. Mechanism and Machine，Theory. 1994，29(8):1151 -1165.

［6］肖铁英，袁盛治，陆卫杰.行星齿轮机构均载系数的计算方法［J］. 东北重型机械学院学报. 1992，10 (4):290 -295.

［7］陆俊华，李斌，朱如鹏. 行星齿轮传动静力学均载分析［J］.机械科学与技术.2005，24(6):702 -704.

［8］周慧琴，李素有，吴立言. 行星齿轮传动系统均载分析［J］.机械科学与技术.2008，27(9):1239 - 1242.

［9］邵晓荣. 齿轮制造及安装误差对行星齿轮均载系数的影响［J］. 东北重型机械学院学报. 1994，18(4):306-309.

［10］杜进辅，方宗德，王宝宾，等.基于变性协调的行星轮系均载特性研究［J］. 航空动力学报. 2012，27 (5):1165 -1171.

［11］叶福民，朱如鹏，鲍和云.非等模数非等压力角NGW 型行星齿轮系静力学均载行为［J］.航空动力学报.2012，27(5):1960 -1965.