基于三轴试验的非饱和土抗剪强度影响因素分析

邓钟尉

(广州市城市规划勘测设计研究院，广东 广州 510060)

1 引 言

吸力［1］是非饱和土力学研究的基础性课题，非饱和土土力学的各种理论(如强度、渗流、变形等)基本上都是围绕吸力这一概念展开的，而对各种吸力的概念和本质认识的正确与否，直接影响到非饱和土有效应力原理及抗剪强度理论的建立。非饱和土的物理参量具有多变性，而且气液收缩膜的物理化学性质也相当复杂，因此，有关非饱和土的抗剪强度理论，学术界尚无法达成共识，汤连生团队［2～5］的研究结果表明:基于湿吸力及结构吸力的非饱和土有效应力原理概念清晰，物理意义明确，初步阐明了A．W．Bishop 单应力状态变量［6，7］中参数χ 和D．G．Fredlund 双应力状态变量［8，9］中tanФb 的物理意义，基于粒间吸力的非饱和土抗剪强度理论，一方面统一了前人的研究成果，另一方面避免了在研究非饱和土强度理论中存在的误区，逐渐为国内外的众多学者所接受。

文献［10～12］对湿吸力、结构吸力分别与非饱和土含水量、饱和度、干密度、孔隙比等常用物性指标或三相比例指标间的关系进行了研究，并进行了定量计算，研究表明，非饱和土的抗剪强度受含水量、干密度和孔隙比的影响较大。本文将通过三轴剪切试验，对不同含水量和干密度的重塑非饱和土进行试验测试，并对验结果进行分析，探讨抗剪强度指标随含水量和干密度的变化规律。

2 试验方法和试样制作

从理论上分析，在误差范围内，根据土的连续性和各向同性假设，土体的物理状态可以用水分状态及密度状态联合表示。因此，本文用含水量w 和干密度ρ这两个变量联合表征非饱和土体的物理状态，而孔隙比e 可通过这两个变量衍生出来，因此，本文只开展控制含水量w 和干密度ρ 的抗剪强度试验。若控制土体的干密度为定值，改变土体含水量w，可塑造出饱和度不同的非饱和土;若控制土体的含水量w 为定值，改变土体的干密度，同样可塑造出饱和度不同的非饱和土。把不同的水分状态与密度状态进行组合，可得到饱和度不同的非饱和土，其抗剪强度的大小也有差异。

试验土样采用重塑非饱和土，采用TSZ－1 型应变控制三轴仪，分别开展了控制含水量和干密度的不固结不排水剪切试验。

2.1 试验方法

本次试验分别在围压50 kPa、100 kPa、150 kPa和200 kPa下进行，载荷加载速率为0.4 mm/min，为防止水分蒸发，当对第一个样品进行试验时，另外的样品用保鲜膜包裹。试样分别在50 kPa、100 kPa、150 kPa、200 kPa的围压下，逐渐加载竖向应力，试样每产生0.5%的轴向应变，测计一次测力计读数和轴向变形值，直到土样破坏后者应变达到特定的数值。记录试样破坏时轴向变形和主应力差，试验结束后根据摩尔库仑定律求得土体的抗剪强度参数。

2.2 试样制备

试样严格按照《土工试验方法标准》(GB/T50123－1999)重塑土的制备程序进行。试验土样为圆柱形试样，试样尺寸直径为39.1 mm，高为80 mm。试验用土的基本物理参数如表1 所示。

试验用土的基本物理参数表 表1

控制含水量试验的每个土样干密度为1.70 g/cm3，制备含水量分别为5%、10%、15%、20%、25%的土样。土样的体积为3.91×8.0 cm3，则每个土样中土的质量为59.82 g，对应水的质量分别为:2.99 g、5.89 g、8.97 g、11.96 g、14.96 g。控制干密度试验的每个土样含水量为10%，制备干密度分别为1.4 g/cm3、1.6 g/cm3、1.8 g/cm3、2.0 g/cm3的土 样。由公式ρ=ρd(1+w)可求得对应土样密度值分别为1.54 g/cm3、1.76 g/cm3、1.98 g/cm3、2.20 g/cm3。土样的体积为3.91×8.0 cm3，每组土样对应质量为90.72 g、103.68 g、116.64 g、129.6 g。

3 试验结果分析

3.1 控制含水量的三轴试验结果分析

试验结果如图1～图5 所示，由试验曲线可以看出，随着含水量的增大，非饱和土的抗剪强度明显减小，说明含水量对非饱和土强度有较大的影响。根据文献［11］的计算结果，湿吸力随含水量增大先递增后递减，结构吸力随含水量增大逐渐减小，在对应的含水量区间内，粒间吸力(湿吸力和结构吸力之和)随着含水量的增大逐渐减小，因此，在相同的围压和主应力作用下，土体的有效应力减小，从而导致土体的抗剪强度降低，理论分析和试验结果是相吻合的。

在围压较小时(50 kPa、100 kPa)，应力－应变曲线都呈现应变软化的特点，含水量越低，应变软化的特性越明显，如图1 和图2 所示。随着含水量的增大，尤其是含水量增大到最佳含水量附近(w=15%、w=20%)时，除围压50 kPa以外，应力－应变关系曲线均呈现应变硬化的特点，如图3 和图4 所示，说明最佳含水量是应力－应变关系从软化转为硬化的临界点。当含水量进一步增大到接近饱和时，应力－应变曲线又转为应变软化，如图5 所示。

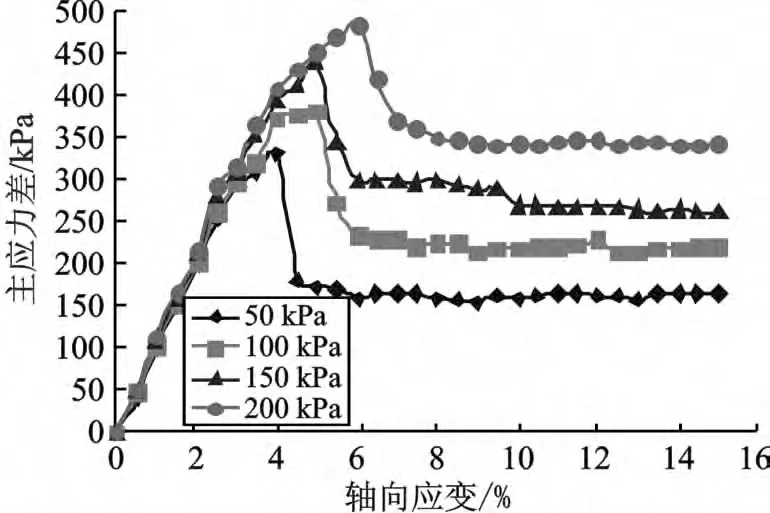
图1 含水量w=5%轴向应变－主应力差曲线

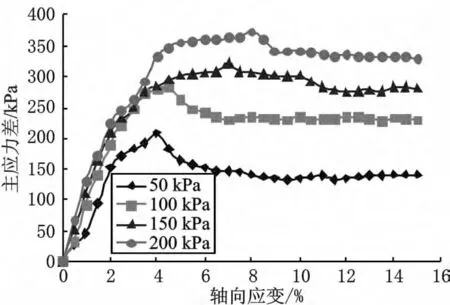
图2 含水量w=10%轴向应变－主应力差曲线

图3 含水量w=15%轴向应变－主应力差曲线

图4 含水量w=20%轴向应变－主应力差曲线

图5 含水量w=25%轴向应变－主应力差曲线

由于直接确定强度包线与摩尔圆的切点坐标存在困难，因此本文以主应力差的峰值为破坏点，当应力－应变曲线没有峰值时，取轴向应变为15%时的主应力差为破坏点。不同含水量状态下，剪应力－主应力关系曲线如图6 所示。根据线性拟合结果，可求得线性拟合方程参数c*和φ*，如表2 所示:

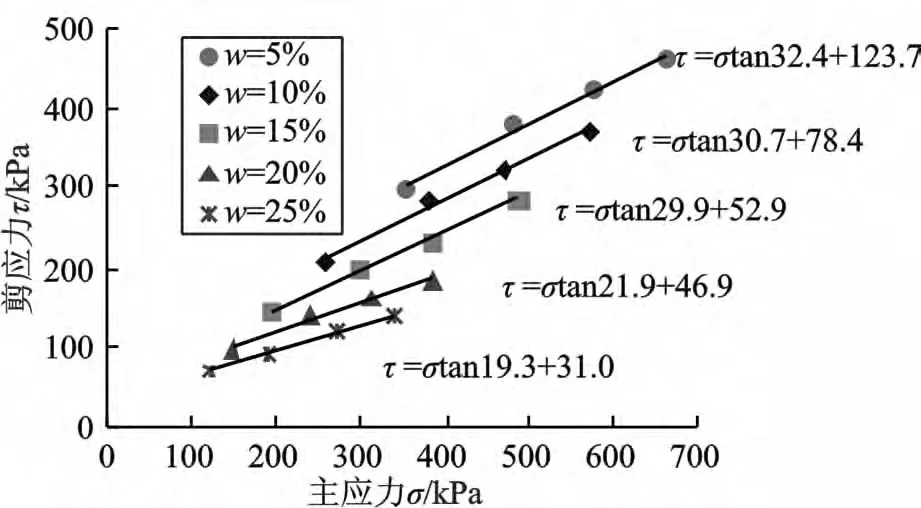
图6 控制含水量的剪应力－主应力关系曲线

不同含水量下三轴试验强度参数 表2

抗剪强度参数和线性拟合参数间的关系如图7 所示，根据几何关系可得:

sinφ=tanφ*(1)

c/tanφ=c*/tanφ*(2)

整理得:

φ=arcsin(tanφ*)(3)

c=c*/cosφ(4)

根据式(3)、式(4)及图7 线性拟合结果，可得不同含水量下土体的抗剪强度参数c 和φ，如表2 所示。

图7 抗剪强度参数和线性拟合参数关系图

整理抗剪强度参数c 和φ 时发现，粘聚力c 随含水量增大呈指数递减，内摩擦角φ 随含水量增大呈线性递减，如图8 和图9 所示。根据非饱和土粘聚力的产生机制，粘聚力c 主要由原始粘聚力、固化粘聚力和毛细粘聚力组成，根据三者与含水量w 之间的变化关系，从湿吸力和结构吸力的角度分析，粘聚力随含水量的增大而逐渐单调减小［10～11］，这与三轴试验结果相符合。内摩擦角主要由土颗粒表面摩擦力与土颗粒之间的咬合力产生的，随着含水量的增大，由于水的润滑作用，土颗粒之间表面摩擦力和咬合力减小，因而内摩擦角逐渐变小，由于土颗粒之间的相对滑动受含水量变化影响较小，所以内摩擦角的变化幅度比内粘聚力小。

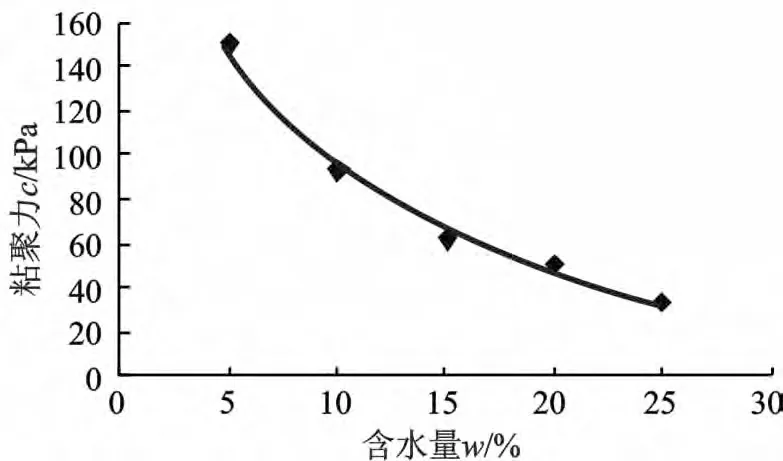
图8 粘聚力c 随含水量w 变化关系曲线

图9 内摩擦角φ 随含水量w 变化关系曲线

3.2 控制干密度的三轴试验结果分析

试验结果如图10～图13 所示，由试验曲线可以看出，随着干密度的增大，非饱和土的抗剪强度明显增大，说明干密度对非饱和土强度有较大的影响。随着土体干密度的增大，单位体积土体内的土颗粒数目增加，单位面积土体上的接触点数目随之增多，湿吸力和结构吸力增大，从而使土体内的有效应力增大，土体的抗剪强度随之增大，理论分析和试验结果是相吻合的。

在干密度较小时(1．4 g/cm3、1．6 g/cm3)，应力－应变曲线呈现应变硬化的特点，干密度越小，应变硬化的特性越明显，如图10 和图11 所示。随着干密度的增大，尤其是干密度增大到最大干密度附近(1.8 g/cm3)时，除围压50 kPa以外，应力－应变关系曲线均呈现应变软化的特点，如图12 所示，说明最大干密度是应力－应变关系从硬化转为软化的临界点。当干密度大于最大干密度时，应力－应变曲线又转为应变软化，如图13 所示。

图10 干密度ρd=1．4 g/m3轴向应变－主应力差曲线

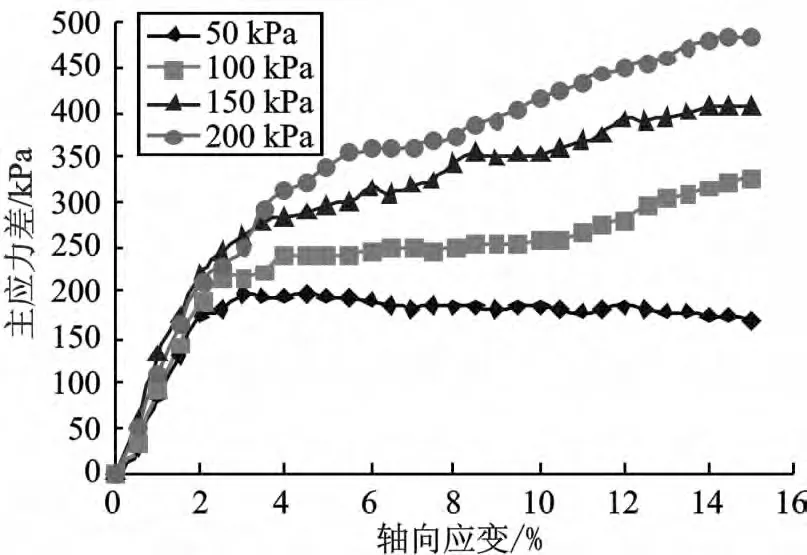
图11 干密度ρd=1．6 g/m3轴向应变－主应力差曲线

图12 干密度ρd=1．8 g/m3轴向应变－主应力差曲线

图13 干密度ρd=2．0 g/m3轴向应变－主应力差曲线

不同含水量状态下，剪应力－主应力关系曲线如图14 所示。根据线性拟合结果，可求得线性拟合方程参数c*和φ*，如表3 所示:

图14 不同干密度下剪应力－主应力关系曲线

根据式(3)、式(4)及图15 线性拟合结果，可得不同含水量下土体的抗剪强度参数c 和φ，如表3 所示。

不同干密度下三轴试验强度参数表 表3

粘聚力c 和内摩擦角φ 均随干密度的增大呈线性增大，但内摩擦角变化的幅度较小，如图15 和图16 所示。干密度越大，单位体积土体内土颗粒数目越多，单位面积接触点数目越多，从而导致湿吸力增大，原始粘聚力随之增大;同理，结构吸力也随单位面积接触点数的增多而增大，导致固化粘聚力也随之增大;因此，土体粘聚力c 随着干密度的增大而递增。

内摩擦角φ 随着干密度变化的趋势与粘聚力较相似，主要原因是随着干密度的增大，单位体积土体内的土颗粒数目增多，土颗粒之间相互嵌套，土颗粒之间的相互连接和咬合更为紧密，连锁作用增强，从而导致内摩擦角增大。

图15 粘聚力c 随干密度ρd变化关系曲线

图16 内摩擦角φ 随干密度ρd变化关系曲线

4 结 论

本文从室内试验的角度出发，研究了非饱和土抗剪强度与土体含水率和干密度的关系，研究结果表明:在外应力相同的情况下，随含水量的增大，土体的抗剪强度单调递减;随干密度的增大，试样的抗剪强度单调递增。最佳含水量是应力－应变关系从软化转为硬化的临界点;最大干密度是应力－应变关系从硬化转为软化的临界点。

随含水量的增大，非饱和土的抗剪强度参数粘聚力呈指数递减，内摩擦角呈线性递减;随干密度的增大，粘聚力和内摩擦角均呈线性增大，但内摩擦角变化的幅度较小。

该试验研究结果成功解释了“在一定的土体含水率变化范围内，非饱和土的强度随含水率的增加而先增大后减小”的事实。

［1］Fredlund D G，Rahadjo H．Soil mechanics for unsaturated soils［M］．NewYork:John Wiley and Sons，1993．

［2］汤连生，王思敬．湿吸力及非饱和土的有效应力原理探讨［J］．岩土工程学报，2000，22(1):83～88．

［3］汤连生．结构吸力及非饱和土的总有效应力原理探讨［J］．中山大学学报，2000，39(6):95～100．

［4］汤连生．从粒间吸力特性再认识非饱和土的抗剪强度理论［J］．岩土工程学报，2001，23(4)

［5］汤连生，颜波，张鹏程等．非饱和土有效应力及有关概念的解说与辨析［J］．岩土工程学报，2006，28(2):216～220．

［6］Bishop．A．W．The principal of effective stresses lecture delivered in Oslo，Norway，1955，printed in Teknisk，Ukblad，1959，106(39):859～863．

［7］Bishop．A．W．，Blight G．E．Some aspects of effective stress in saturated and partially saturated soils［J］．Geotechnique，1963，13(3):177～197．

［8］Fredlund．D．G and Morgenstern．N．R．Stress state variables for unsaturated soils［J］．Journal of the Geotechnical Engineering Division，Proceedings，ASCE(GTS)，1977，103:447～466．

［9］Fredlund．D．G，Xing．A．，Barbour．S．L．The relationship of the unsaturated soil shear strength to the soil－water characteristic curve［J］．Can．Geotech．J．1995，32:440～448．

［10］张鹏程，汤连生，邓钟尉等．非饱和土粒间吸力研究的若干思考和进展［J］．水文地质与工程地质，2012，39(2):30～36．

［11］张鹏程，汤连生，邓钟尉等．非饱和土湿吸力与含水量的定量关系研究［J］．岩土工程学报，2012，34(8):1454～1457．

［12］张鹏程，汤连生，姜力群等．基质吸力与含水量及干密度定量关系研究［J］．岩石力学与工程学报，2013，32(S1):2793～2797．