秩亏自由网序贯平差及各模型比较分析

陆建华，徐克成

(1.苏州市测绘院有限责任公司，江苏 苏州 215000;2.中国矿业大学环境与测绘学院，江苏 徐州 221116)

1 引 言

若在原来控制网的基础上进行扩建或对旧网进行复测，可按序贯平差原理进行平差［1］，它可充分利用前期平差结果与当前观测样本，无需存储历史观测数据，无需求大矩阵逆就能获得与整体平差相同的最优解，具有计算公式简洁、规律性强、计算量小的特点［2］。但如果前期平差为秩亏自由网平差结果，则其权逆阵不存在，问题就变为秩亏自由网的序贯平差。

本文对第一次平差后得到虚拟观测值的权逆阵进行了适当变换，得到了其权阵PX，的计算通式，解决了秩亏问题，可为变形监测等分期完成的测量工程提供可取的数据处理方法。然后，详细阐述了重心基准自由网平差、拟稳平差模型，并通过实例计算对其平差结果进行比较分析，得出了相关结论。

2 序贯平差基本原理

序惯平差是指将观测值分成两组或多组，按组的顺序分别做相关间接平差，从而使其达到与两期网一起做整体平差同样的效果。分组后法方程阶数降低，减轻了计算强度，以下以分两组为例介绍其基本原理及平差过程［3］。

上式中，Li为观测值，B 为系数阵，d、l 为构成函数关系式的常数项。

按间接平差原理，先对第一组误差方程进行第一次平差，其法方程为:

可解得第一次平差后未知参数和观测值的改正数，分别为:

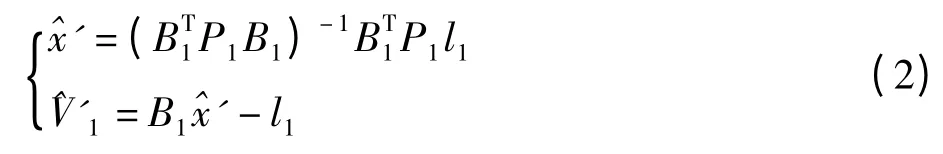
再对第二组误差方程做第二次平差，此时将第一次平差后得到的参数为初值)作为虚拟观测值参与平差，其权阵为。误差方程为:

联合第二组误差方程，可得法方程:

即：

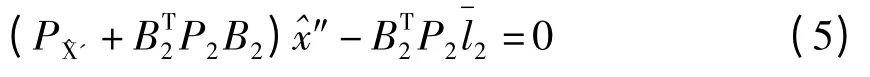
可解得第二次平差后未知参数和观测值的改正数，分别为:

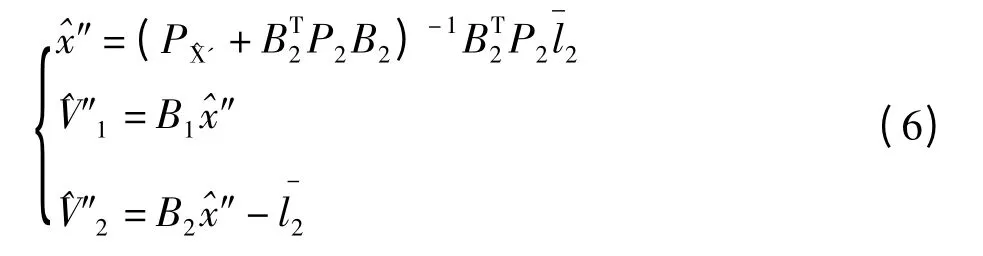
最后平差值为:

3 秩亏自由网序贯平差模型

当监测网中没有必要的起算数据时，应用序贯平差进行数据处理得到的前期平差结果作为虚拟观测值的权阵不存在，变为秩亏自由网的序贯平差问题。以下进行了适当变换，给出了虚拟观测值权阵的计算方法，解决了秩亏问题。

3.1 权逆阵计算

当网中存在秩亏时，为获得未知参数的唯一解可给定加权基准约束条件:，因此平差模型变为:

将S 标准化为G，使满足:GTPxG=E

则可解得:

则按协因数传播定律，有:

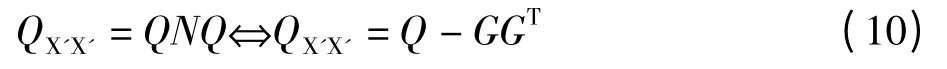
由于平差结束后QX'X'可求出，所以整理得:

即:

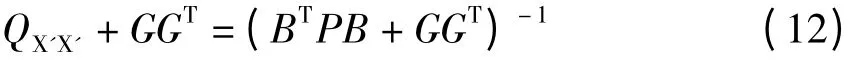
两边求逆并移项可得:

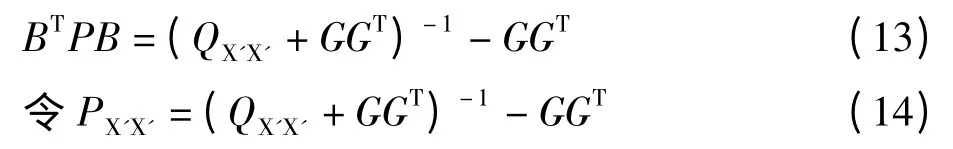
可以容易的证明，当将第一期平差结果作为虚拟观测值，并按上式给出其权阵，与新增观测值一起平差，可以得到与整体平差一样的结果。所以式子:

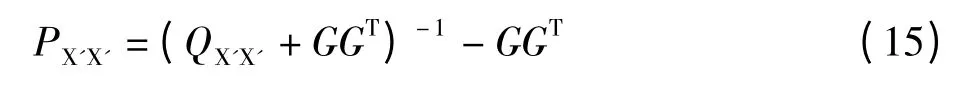
可以作为秩亏自由网序贯平差虚拟观测值权阵的计算通式。

当虚拟观测值的权阵确定以后，按上节中序贯平差原理进行第二次平差，即可计算得到观测值及参数的改正数，解决了秩亏问题。

3.2 平差模型

附加基准条件的秩亏自由网平差，当选择的基准不同时其平差模型也不同，以下介绍基于重心基准的秩亏自由网平差和拟稳平差模型［4］。

(1)重心基准秩亏自由网平差

采用重心基准，其基准权为单位阵，Px=E，又称为普通秩亏自由网平差［5］。

由式(8)可得平差模型变为:

由式(9)、式(10)得模型的参数估计为:

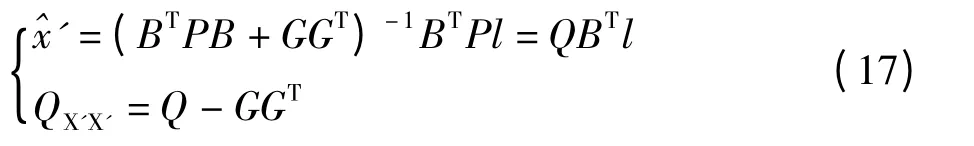
(2)拟稳平差

其基准权为:

基准约束为:

则拟稳平差的基准约束条件为:

所以，拟稳平差的平差模型为:

由式(9)、式(10)得拟稳平差模型的参数估计为:

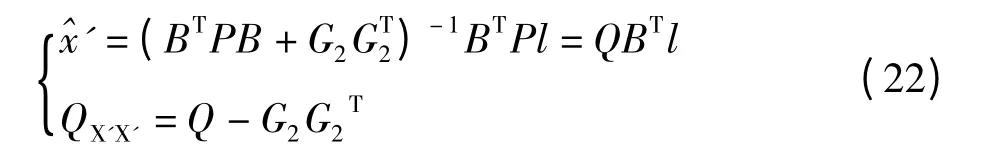
拟稳平差模型是将全部网点分为两部分X1、X2，X2是拟稳点组成的参数，基准约束条件式(20)中仅包含X2，所以拟稳平差实质是拟稳点组的重心基准［6］。

4 算例分析

算例一:设有水准网如图1 所示，一期观测了h1，h4，h5，平差后高程的协因数阵为:

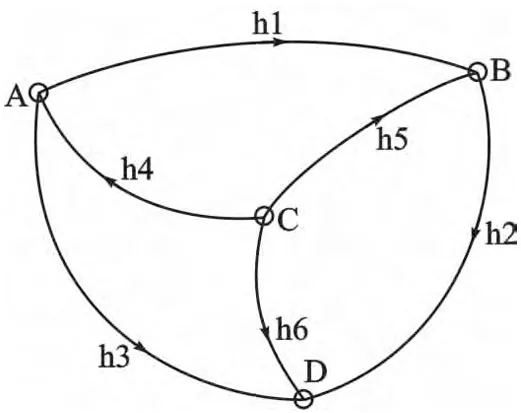
图1 实例一观测水准网示意图

观测高差、距离和各待定点高程近似值如表1 所示。

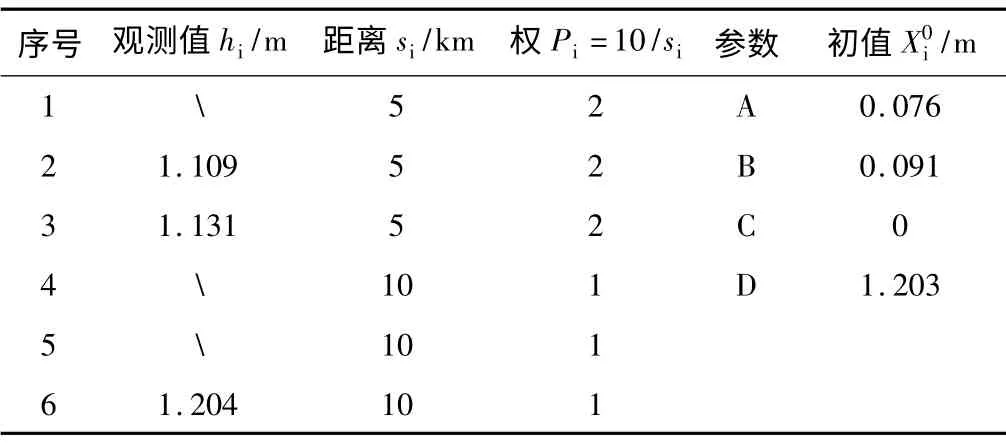
观测高差、距离和待定点近似值 表1

当选择重力基准秩亏自由网平差模型时，根据算例第一期水准网有3 个未知点，则:

由式(14)可得:

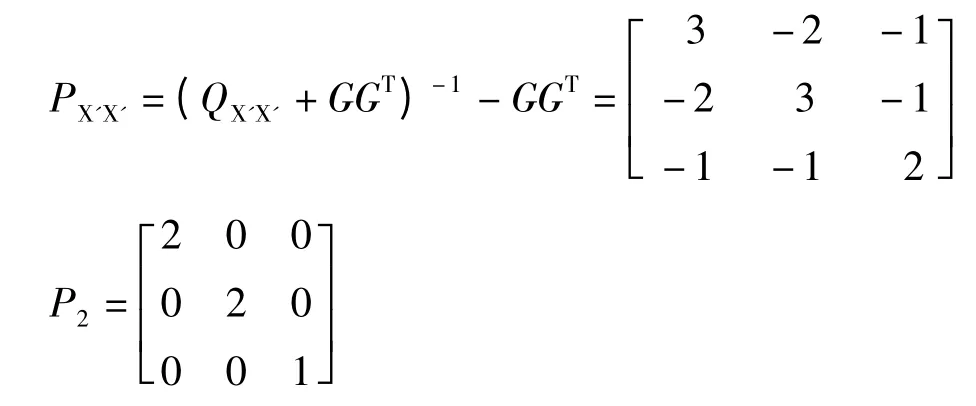
第二期观测误差方程式为:

由式(6)可得:

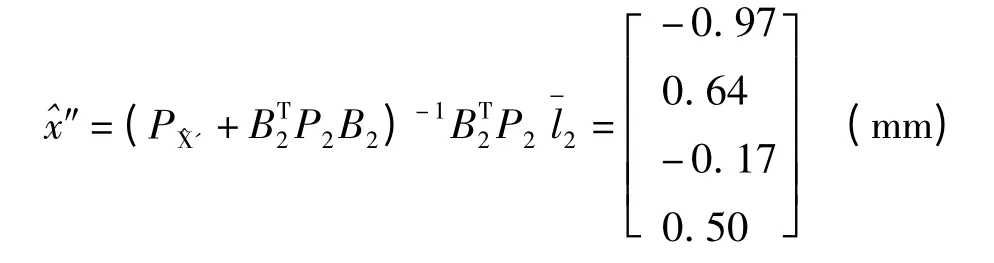
由式(7)可得:

算例二:设有水准网如图2 所示，其中各观测高差、距离和各待定点高程如表2 所示，分别进行以F 点为固定点的经典自由网平差、以重心基准的秩亏自由网平差及以A、B、E、F 为拟稳点的拟稳平差。

图2 实例二观测水准网示意图

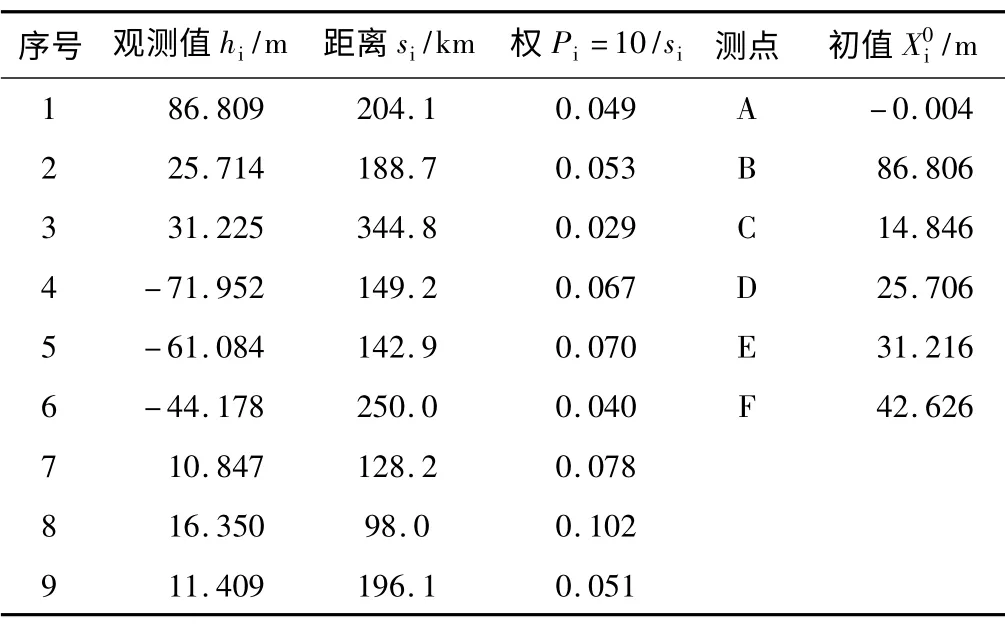
观测高差、距离和待定点近似值 表2

根据算例可得误差方程为:

以重心基准进行自由网平差，Px=E 水准网有6点，则:

以A、B、E、F 为拟稳点进行拟稳平差时，Px=diag［1 1 0 0 1 1］，则:

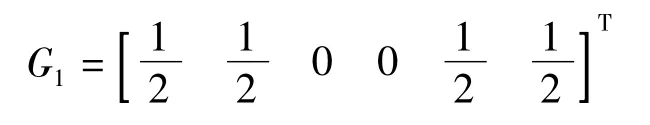
根据式(17)、式(22)，应用matlab 7.0 编程实现，经演算得到结果如表3 所示:

观测高差、距离和待定点近似值 表3

未知参数估值的协因数阵为:

对结果进行分析，可知:经典自由网平差、重心基准自由网平差和拟稳平差所得观测值改正数相同，且均满足VTPV=min;重心基准自由网平差，tr(QX'X')=min;拟稳平差。

5 结 论

(2)经典自由网平差、重心基准自由网平差和拟稳平差所得观测值改正数相同，且均满足VTPV=min。

(4)拟稳平差满足

［1］张书毕，单世坤，王坚．秩亏自由网逐次平差及其应用［J］．测绘通报，2001，8:26～28．

［2］曾安敏，张丽萍．多种序贯平差方法的比较［J］．大地测量与地球动力学，2007，27(2):84～87．

［3］葛永慧．测量平差［M］．徐州:中国矿业大学出版社，2005．

［4］崔希璋等．广义测量平差［M］．武汉:武汉大学出版社，2009．

［5］邱飞廷，董坤烽，李朝光等．带基准权的秩亏自由网平差及其应用［J］．江西科学，2010，28(5):666～668．

［6］万斐，陈艳艳．拟稳平差在测量数据处理中的应用［J］．地理空间信息，2008，6(6)．