在电磁学体系下讨论运动电荷的电场与磁场的联系

谷建生 李 宏 魏 环 莫文玲

(河北联合大学理学院 河北 唐山 063000) (河北联合大学以升创新教育基地 河北 唐山 063000)

静止电荷产生电场，运动电荷还能产生磁场，这是大学物理教材中的基本教学内容.但两者之间的相对性，一般的大学物理教材不涉及，或者虽有涉及，但几乎无一例外地是在狭义相对论基础上，先得到电磁场的相对论变换，然后再讨论运动电荷产生电场和磁场的联系.物理专业用的电磁学教材[1,2]和一些文献[3,4]也基本上是按这个思路对此问题进行讨论.本文以运动电荷相对导体圆环运动为例，在麦克斯电磁理论的体系下，阐明运动电荷产生的电场和磁场之间的联系，以展示电磁场的相对性.

图1 点电荷和导体圆环相对运动时，不同参考系感受到电场和磁场的不同

如图1所示，当点电荷相对导体圆环以速度v向右运动时，不同参考系会感受到不同的电场和磁场.若以圆环为惯性参考系，如图1(a)所示，该系不仅感受到了电场E，而且也一定会感受到磁场B，因为电荷运动就形成了能激发磁场的电流.若以点电荷为惯性参考系，相当于圆环向左运动，如图1(b)所示，该系只感受到静电场E′，不会感受到磁场B′，即B′=0.那么圆环系下所感受到的这个磁场B是独立的吗？还是与电场E有什么联系呢？下面在圆环系下展开讨论.

在圆环系下，由麦克斯韦位移电流假说，有如下的安培环路定理

(1)

其中L是圆环本身所构成的回路，S是以圆环为边界所构成的曲面，上式可展开为

∬SE(t)•dS

(2)

其中的E(t)和E(t+dt)为圆环系不同时刻感受到的电场，如图2中(a)和(b)所示.麦克斯韦方程组在不同惯性系下都成立，所以圆环系下电场要满足高斯定理，但要注意圆环系下电场是随时间变化的，所以我们要用某一时刻电场的高斯定理，这里用时刻t+dt电场E(t+dt)的高斯定理

∬侧面E(t+dt)•dS+∬SE(t+dt)•dS+

∬S(t+dt)E(t+dt)•dS=0

(3)

高斯面的选择如图2(c)所示，其中的S(t+dt)是假设圆环与电荷一起运动时，t+dt时刻圆环所围的曲面，图中用虚线表示，高斯面内显然不包围电荷.高斯定理中S(t+dt)和S的正方向都是沿高斯面的外法线方向，现在改变S(t+dt)的正方向以与S的正方向一致，则由式(3)有

∬侧面E(t+dt)•dS=-∬SE(t+dt)•dS-

∬S(t+dt)E(t+dt)•dS

(4)

图2

注意比较图2(c)和(a)可以看出，t+dt时刻电场E(t+dt)通过S(t+dt)的电通量等于t时刻电场E(t)通过S的电通量，即

∬S(t+dt)E(t+dt)•dS=∬SE(t)•dS

(5)

将式(2)、(4)和(5)三式联立，就可得到

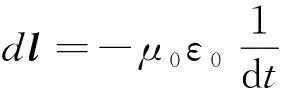
(6)

由矢量运算法则有

E(t+dt)•dS=dS•E(t+dt)=

-dl×vdt•E(t+dt)

(7)

将式(7)代入式(6)，式(6)右面的面积分化为沿圆环的线积分，得到

(8)

将式(8)中的前两个dt直接消去并令最后一个dt→0，就得到

∮LB•dl=μ0ε0∮Ldl×v•E(t)=

μ0ε0∮Ldl×v•E=

μ0ε0∮Lv×E•dl

(9)

上式中的E(t)直接换为E，因为这就是电场和磁场之间的瞬时关系，再利用光速c与μ0，ε0的关系，由式(9)可得

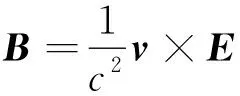
(10)

上式表明，圆环系虽然感受到了磁场B，但这磁场并不是独立的，与该系感受到的电场E有关，且满足式(10).实际上，无论是点电荷动还是圆环动，都只是参考系选择的不同，按相对性原理，两种情形就不应该有根本的差别.既然点电荷系肯定没有感受到磁场，而圆环系却肯定感受到了磁场，那么磁场的有无就只能成为相对的了.式(10)的结论也支持了这点，这说明电场和磁场实际上是同一客体——电磁场在不同参考系下的不同反应而已.此例在麦克斯韦电磁理论的体系下，既给出了运动电荷所产生电场和磁场之间的联系，也很好地展示了电磁场的相对性.

参考文献

1 赵凯华，陈熙谋．电磁学(上册)(第二版)．北京：高等教育出版社，1985

2 贾起民，郑永令，陈暨耀．电磁学(第二版)．北京：高等教育出版社，2001

3 郑永令．运动电荷的磁场与毕奥-萨伐尔定律. 大学物理，1993(4):3～6

4 张贵银，陈素敏．简析运动电荷的场. 物理通报，1998(8)：42