电偶极子激发的电场及其MATLAB软件的模拟仿真

矫洪楠 侯 恕

(东北师范大学物理学院 吉林 长春 130024)

1 MATLAB简介

1.1 MATLAB软件

MATLAB是MathWorks公司推出的用于科学和工程计算的交互式软件系统.它以矩阵作为数据操作的基本单位,提供数值计算函数,具有强大的数值计算与分析功能. MATLAB 与符号计算语言Maple结合,从而具有符号计算功能. MATLAB还具有绘图功能,也可以对图形进行修饰和控制,其数据处理能力和工具箱亦使得用它编程比传统的编程问题容易、简便[1].因此, MATLAB既是一种编程环境,又是一种程序设计语言,与高级程序语言C和Fortran相比更加数学化,使用起来也更方便,但是MATLAB是解释性语言,程序执行速度较慢,而且不能脱离MATLAB环境而独立运行.

1.2 用MATLAB模拟电偶极子场分布的优点

首先用MATLAB可以实现模拟电偶极子周围场分布,以实现物理模型的可视化.其次，给定空间任意一点坐标，即可用给定的公式计算这一点的电位，对电位求梯度可得到空间任意一点的场强表达式.再次，可以用MATLAB实现电偶极子近区场分布的模拟以及远区辐射场的模拟，这对于充分理解电偶极子的场分布具有重要的作用.

2 偶极子简介

2.1 电偶极子

电偶极子是指一对等值异号的点电荷相距一微小距离所构成的电荷系统，它是一种常见的场源存在形式.它同点电荷、分子电流等一样是电磁学中的一个重要物理模型.特别是在电介质极化理论及天线理论中,电偶极子是一个基本模型[2].

2.2 电偶极子激发的远区场

图1表示中心位于坐标系原点上的一个电偶极子，它的轴线与z轴重合，两个点电荷q和-q间的距离为L.此电偶极子在场点P处产生的电位等于两个点电荷在该点的电位之和，即

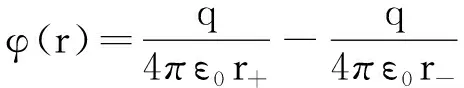
(1)

其中r+与r-分别是q和-q到P点的距离.

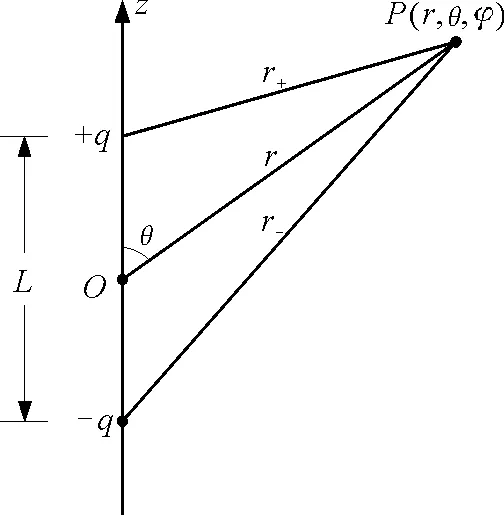
图1 电偶极子

一般情况下，我们关心的是电偶极子产生的远区场，即电偶极子到场点的距离r远远大于偶极子长度L的情形，此时可得到电偶极子的远区表达式

(2)

可见电偶极子的远区电位与qL成正比，与r的平方成反比，并且和场点位置矢量r与z轴的夹角θ有关.

为了便于描述电偶极子，引入一个矢量p，该矢量的模p=qL，方向由-q指向q，称之为此电偶极子的电矩矢量，简称为偶极矩，记作

p=qL

(3)

此时式(2)又可以写成

(4)

电偶极子的远区电场强度可由式(4)(球坐标系)求梯度得到.因电位φr只是坐标r和θ的函数，于是有

E=-

(5)

从式(4)和式(5)可以看到，电偶极子的远区电位和电场分别与r的平方和r的三次方成反比.因此，其电位和场强随距离r的下降比单个点电荷更为迅速，这是由于两个点电荷q和-q的作用在远区相互抵消的缘故.

根据式(4)，电偶极子的等电位面方程可由式(2)为定值得到.

将电场线微分方程写成球坐标形式，并注意此时电场只有r和θ两个分量，有

(6)

把电场表达式(5)带入式(6)，得

(7)

解式(7)得

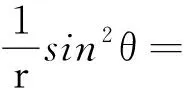
(8)

式(8)即是电偶极子远区场的电场线方程.

图2绘出了电偶极子在φ为常量的平面内，式(8)取不同的常量所对应的等电位线和电场线.

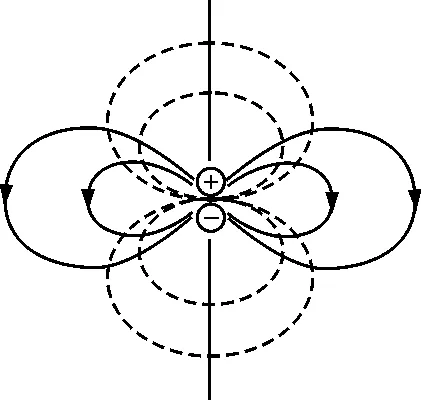
图2 电偶极子的电场线与等位线

需要说明的是图中准确的只是电场线的形状，电场线的疏密并不严格与场强成正比，只是疏的地方场强小些，密的地方场强大些而已.

前面讨论了电偶极子的中点位于坐标系原点且偶极矩方向为z方向的情况.对于中点不在原点和偶极矩非z方向的一般情况，通过与前面类似的推导，可以得到远区的电位

(9)

其中，er是电偶极子中心指向场点P的相对单位位置矢量，偶极矩p=qL，L的方向依然规定为从-q到q.

经推导还可得到远区场的电场强度表达式

E=-

(10)

由式(10)可以看出,电偶极子的电场线均分布于子午面上,即由r,θ构成的平面上,并且任意一个子午面上的电场线分布都相同.

从以上几种不同情况下电偶极子在空间激发的电场结果来看, 电场强度与p=qL成正比, 与源点到场点的距离r的三次方成反比,电偶极子在远处的性质是由其电偶极矩来表征的. 电偶极矩是电偶极子的重要特征. 研究电偶极子在空间激发的电场为分析电介质的极化现象、电磁波的发射、吸收以及辐射等奠定了重要的理论基础.

3 MATLAB软件模拟电偶极子过程

3.1 建立模型

空间任意一点的电位为

在直角坐标系中可确定r+及r-与空间任意位置坐标的关系

(11)

因此，只要给定空间任意一点的位置坐标P(x，y，z)，就可以算出这一点的电位.

3.2 流程图

程序流程图如图3所示，其主要步骤如下.

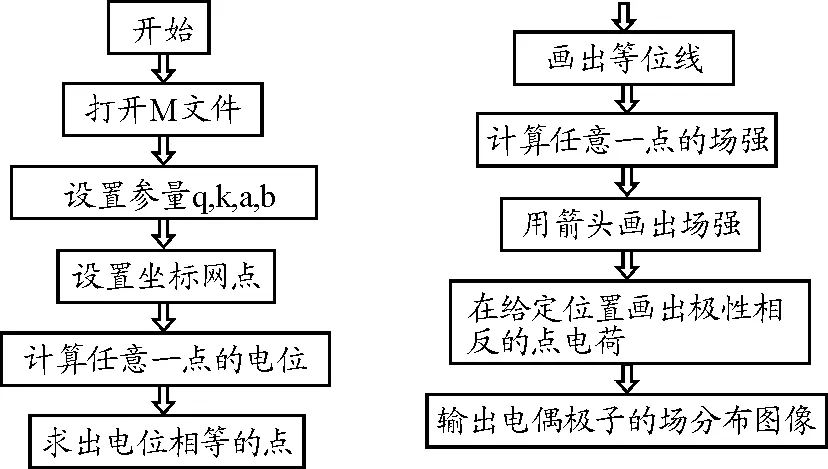
图3

3.3 演示程序及图形

用MATLAB模拟电偶极子场分布(二维情况)的程序(略).

用MATLAB模拟电偶极子场分布(三维情况)的程序如下：

clear;

b=1.5;

x=-10∶0.6∶10;

y=x;

[X,Y]=meshgrid(x,y);

U=(1./rp-1./rn);

clf;

surf(X,Y,U)

box on

axis tight

alpha(0.8)

shading interp

hold on

plot3([0;0],[1.5;-1.5],[0;0],′r′,′LineWidth′,1)

plot3(0,1.5,0,′ro′,0,1.5,0,′r+′)

plot3(0,-1.5,0,′ro′,0,-1.5,0,′r-′)

title(′电偶极子电势三维分布′,′FontSize′,16)

xlabel(′X′,′FontSize′,16)

ylabel(′Y′,′FontSize′,16)

zlabel(′U′,′FontSize′,16)

u=0.5∶0.25∶3;

由以上程序所得到的图形如图4所示.

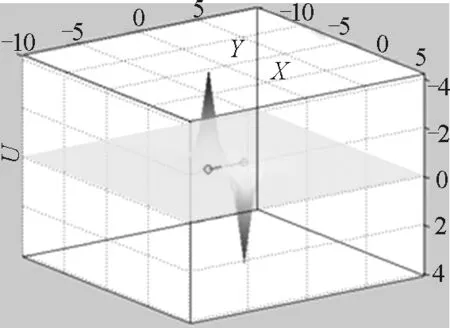
图4 电偶极子电势三维分布图形

4 结果分析

本文得到的电偶极子的场分布图形既形象又直观，模拟的过程简单易懂.在电磁场辐射研究中, 由于电磁场的不可触和不可视性, 使理论过于抽象.电偶极子是研究电磁场辐射过程中最具代表性的物理模型, 如果我们充分地理解了电偶极子的辐射, 就可以更加深入了解电磁波辐射.本文的分析无论用于电磁场辐射的理论研究与说明, 还是用于相关物理现象的探索, 都是非常有意义的.在条件许可的情况下, 也可以用于教学课堂的演示,从而把复杂的物理现象直观地展示出来.

5 需要的改进

通过计算机程序设计,我们对计算机编程技术有了一定的了解,并且对电偶极子这个最基本的物理模型也有了较为深入的认识.虽然用MATLAB得到了电偶极子的辐射模型,结果较为理想,但觉得这些程序还有一些需要改进.

(1)本文得到的电偶极子的场分布图形是静态的,另外,本次设计得到的图形并不十分精确,而仅是给出了电场线的大体形状,因此,如果我们能够得到更加精确的图像，将更加具有现实意义.

(2)模拟出来的图形如果能够采用动画的形式播放,既可以用于教学,又可以给人以视觉上的享受,把抽象的问题具体化、图形化.

参考文献

1 高会生.MATLAB原理与工程应用(第1版).北京：电子工业出版社，2006.107～130

2 陈重.电磁场理论基础 (第3版).北京：北京理工大学出版社,2003.63～70

3 陈军, 田亚兰, 于成，等．ScienceWord软件辅助高中物理教学实践的初级应用．物理教师，2009(2)：39～40