坦克目标RCS统计模型分析

刘增灿，邓爱明，王森

(中国兵器工业第五九研究所，重庆400039)

坦克目标RCS统计模型分析

刘增灿，邓爱明，王森

(中国兵器工业第五九研究所，重庆400039)

为分析和评估目标雷达散射截面(RCS)起伏对雷达检测性能的影响，常用一些统计模型来描述目标RCS的起伏。分析了离散数据统计方法，针对某型坦克目标的目标特性外场实际测量的RCS数据进行统计拟合分析，检验了的RCS统计模型，得到了其RCS起伏的统计分布规律，为地面装备目标特性研究提供重要参考。

雷达散射截面;统计模型;地面装备

目标特性测试外场测量的地面装备雷达散射截面(RCS)是获取其雷达目标特性的一种重要手段，由于地面装备RCS受雷达探测俯角、方位角及测量环境等影响，RCS呈现起伏变化特征，如何从目标RCS测量数据中发现目标雷达起伏分布规律并提取目标特征值，这对雷达有效探测、识别目标非常重要。针对坦克为代表的典型地面装备受到制导导弹、末敏弹等武器多角域下的侦测与精确制导打击威胁，急需开展地面装备目标特性测试与评价技术研究，为提高装备自身防护能力和提升地面装备在信息化条件下的突击作战能力提供技术保障［1］。

由于坦克装甲车辆等典型地面装备目标属于电大尺寸目标，其由多个散射子组成，在其RCS测量中由于受雷达探测俯角、方位角及测量环境等影响，从而导致雷达回波幅度起伏变化，其RCS的起伏是随机的、不规律的［2］。

本文基于某坦克毫米波RCS测量实验，对其RCS测量数据进行平滑简化处理，并在此基础上对其进行统计特征描述，给出统计特征参数和概率密度函数(PDF)及累计概率分布函数(CDF)，并应用雷达目标起伏统计模型对坦克RCS测量数据的概率密度及累积分布曲线进行拟合对比分析，得到了坦克目标的RCS起伏的统计分布规律，并应用电磁散射理论对其进行了解释，可为坦克RCS的设计和减缩提供参考。

1 RCS测量数据统计处理

目标的雷达散射截面是表征雷达目标对于照射电磁波散射能力的一个物理量，是描述雷达目标信息最重要、最基本的一个参数。地面装备是陆地信息战装备系统的活动载体，其RCS是地面装备无源对抗以及威胁规避等决策应用中的重要信息，因而得到低目标特征装备RCS测量的各种特征值以及统计分布规律就显得尤为重要。

1.1 RCS测量数据的统计参数

对于测量得到的RCS数据(σ1，σ2，…，σn)，其主要的经典统计参数定义如下:

1.2 RCS测量数据的统计处理

在统计分析RCS数据时，还需给出概率密度分布(PDF)和累积概率分布(CDF)，有关RCS数据概率密度函数PDF和累积分布函数CDF计算如式(7)、式(8)。

概率密度函数定义为雷达散射面积位于σ0和σ0+dσ之间的概率P为:

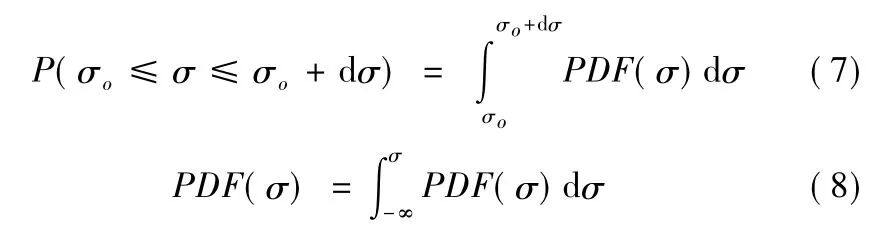
对于离散的RCS测量数据，可按如下方法计算:设在该扇区内出现的RCS最大值和最小值分别为σmax和σmin，将(σmax－σmin)等分为N个值段，值段长为Δ=(σmax－σmin)/ N。在第n(1≤n≤N)值段中，RCS出现的次数记为n，从第1个值段到第n个值段(包括第n个值段)中RCS数据累积出现的次数记为Jn，全扇区内RCS数据个数的总和记为JN，则有:

为了定量准确地描述目标雷达截面积的起伏特性，需要知道它的概率密度函数和相关函数，然后建立相应的RCS起伏统计模型。

2 典型雷达目标起伏特性统计模型

2.1 典型统计模型

为描述目标RCS的起伏特性，学者们建立了各种各样的统计模型，如W.Weinstock，D.P.Mayer与H.A.Mayer等提出一种经典统计模型，其概率密度服从卡方分布模型;施威林(Swerling)模型(是卡方分布模型的特例);对数正态分布、赖斯分布等［3－4］。

其中:2m为其自由度，通常为整数;¯σ是σ的均值。该模型尤其适用于战斗机、民航飞机、直升机及描述很规则形状的物体，如一带翼的圆柱体(如导弹目标)，人造卫星等目标特征。征数据，提高数据分析精度。

对数正太分布的概率密度函数为

卡方分布的概率密度函数为

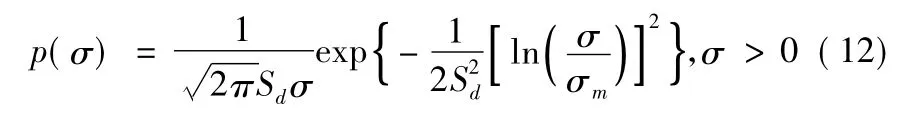
其中:σm为σ的中值，Sd为ln(¯σ/σm)。

对数正太分布表示由电大尺寸的不规则外形散射体组合的物体，如卫星、大的船舰、空间飞行体等。它们常呈现出以下特征:比中值σm大很多的RCS值，虽然出现的概率很小，但随着平均中值比的增大，其概率密度曲线的“尾巴”拖得很长。

莱斯分布的概率密度函数为

式中:J0(·)为零阶修正贝塞尔函数;S是非起伏成分的功率与随机成分总功率之比值(S表示大散射体的截面积与小散射体的总截面积之比)。当参数选择合适时，莱斯功率分布和卡方分布会十分近似，可用卡方分布的结果，对莱斯分布起伏时的性能进行估算。赖斯分布表示由一个定常幅度RCS与多个瑞利散射子组合的目标，s表示稳定体在组合体目标中的权重。

2.2 统计模型的对典型地面装备的适用性

结合某坦克目标的RCS测量试验数据，应用已建立的经典分布模型对其统计分布特性进行拟合，以检验现有模型对典型地面装备雷达目标起伏特性的适应性。对于某目标特性测试场测量的某坦克目标，首先测量其RCS随姿态角变化的数据曲线，然后根据测量的装备雷达目标特性数据提取装备在不同角域的RCS统计参数数据，最后计算目标不同姿态角范围的RCS分布概率密度函数和分布函数，应用现有分布模型拟合其概率密度和分布函数曲线，并与测量数据进行对比以检验模型的适用性［5］。

以某坦克3 cm波段5°测量俯角下的车首(方位165°～195°)和右侧面(75°～105°)RCS测量数据为例(由于坦克左侧面与右侧面对称，其RCS测量数据起伏规律一致，因此这里仅给出坦克右侧面拟合图形)，分别用卡方分布、对数正太分布及莱斯分布模型拟合其概率密度并与RCS测量数据计算的概率密度数据相比较，验证典型模型的对地面装备起伏特性的适用性。3种模型的RCS概率密度拟合曲线如图1所示。

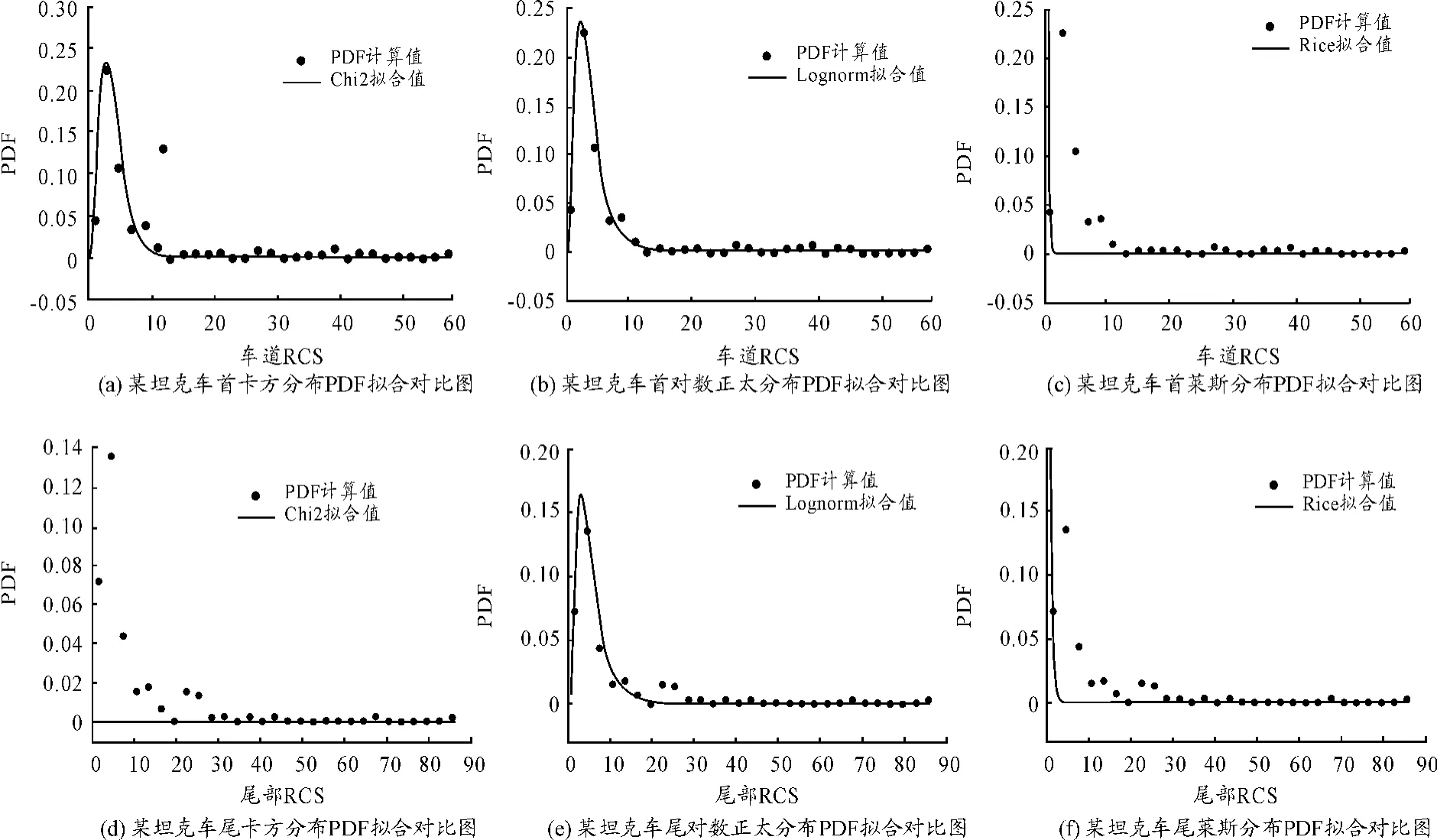
图1 3种模型的RCS概率密度拟合曲线

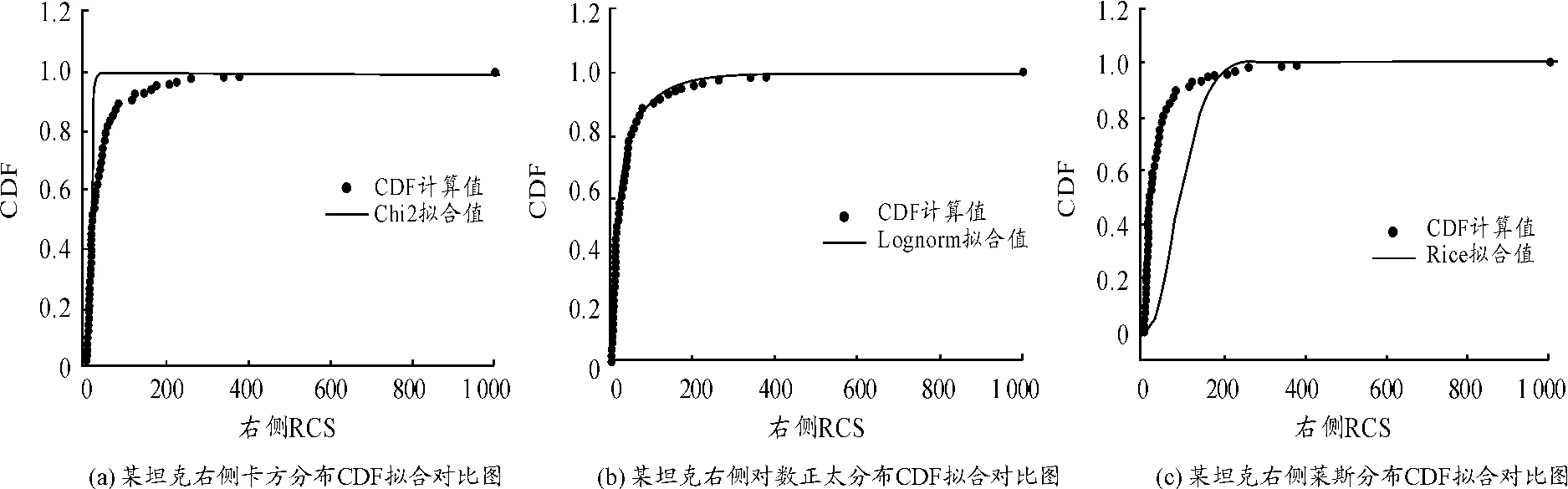
图2 某坦克CDF拟合对比曲线

表1 某坦克车首典型分布模型PDF拟合参数

3种模型RCS概率密度拟合参数如表1所示。表1中SSE表示拟合误差平方和，RMSE表示拟合均方根误差，SSE和RMSE值越接近0说明拟合效果越好;Rsq表示拟合相关系数，Rsq值越接近1，说明拟合效果越好。从图1和图2及表1数据分析可见:

1)在对飞行器目标特性普遍应用、适用性较好的卡方分布模型完全不适用对地面装备雷达目标起伏特性统计分析。如卡方分布对坦克车首部位的概率密度拟合值与RCS测量数据计算的概率密度值拟合相关性为95.7%，而在坦克右侧面的相关性仅为6.88%。

2)由于赖斯分布适用于描述由一个定常幅度RCS与多个瑞利散射子组合的目标起伏特性，而地面装备的雷达目标特性不仅与俯角、方位、极化、装备表面属性相关，其RCS不可能有一个定常幅度，因此莱斯分布也不适合于描述地面装备雷达目标起伏特性，上述图表拟合结果也印证这一说法。因为对坦克车首和右侧面的拟合相关分别仅有11.69%和6.88%。

图3 某坦克车首对数正太分布CDF拟合对比

3)由于对数正太分布表示由电大尺寸的不规则外形散射体组合的物体，如卫星、大的船舰、空间飞行体等，而地面装备也属于电大尺寸的不规则外形散射体的组合物体，因此，莱斯分布模型对坦克的RCS起伏特征拟合效果较卡方分布和对数正太分布好，但在某些角域的拟合相关性较差，如图3所示的对某坦克30°俯角下的车首RCS测量数据的累积分布拟合相关性仅为86.46%，误差平方和为0.109 7。

4)由于目标的复杂性，很难用准确的数学公式表达出目标截面积的概率密度函数，只能用一个既接近又合理的统计模型来描述。卡方分布模型、对数正太分布模型及莱斯分布模型对装备RCS起伏特性分布拟合都有一定的限定条件及适用范围，并且这些统计模型主要针对飞行器及舰船目标，对地面装备的雷达起伏特性拟合效果普遍较差，需要建立新的模型来准确表征地面装备雷达起伏特性。

3 结论

常用的雷达散射特性起伏模型是国内外学者针对飞行器、舰船等目标建立的分布模型，模型是根据大量的目标雷达目标特性实测数据进行统计分析和拟合检验建立的，每种模型都有一定的适用目标及应用边界条件，并不是通用的。实际上很难精确地描述任一目标的统计特性，因此用不同的数学模型只能是较好地估计而不能精确地预测系统的检测性能。本文以典型地面装备某坦克为例，通过对其RCS实测数据进行统计，分析了各种统计模型对典型地面装备的雷达起伏特性分布拟合效果，相比较而言对数正太分布拟合效果较卡方分布和莱斯分布较为适用，而各种模型对典型地面装备的雷达目标起伏特性表征在雷达视角和目标方位等起伏特性表征上具有一定的局限性。因此，下一步的研究目标是根据大量测量积累的典型地面装备RCS数据进行统计分析，建立适用于地面装备的雷达目标起伏特性表征模型，这将对地面装备雷达目标起伏特性研究具有重要的意义。

［1］刘增灿，邓爱明，周学梅，等.目标侦测与伪装技术［J］.四川兵工学报，2011，32(4):30－32.

［2］黄培康，殷红成，许小剑.雷达目标特性［M］.北京:电子工业出版社，2005.

［3］XU Xiaojian，HUANG Peikang.A new RCS statisticalmodel of radar targets［J］.IEEE Trans.AES，1997，33(2):710－714.

［4］JOHNSTONSL.Target fluctuation models for radar system design and performance analysis:An overview of three papers［J］.IEEE Trans.AES，1997，33(2):696－697.

［5］曾勇虎，王国玉，陈永光，等.基于卡方分布的目标RCS起伏特性分析［J］.雷达科学与技术，2007，5(2):115－117.

(责任编辑杨继森)

Analysis of Statistical Model for RCS of Tank

LIU Zeng－can，DENG Ai－ming，WANG Sen
(The No.59 Research Institute of China Ordnance Industry，Chongqing 400039，China)

To analyze and evaluate the effect of target’s RCS fluctuation on the performance of radar detection，a series of statisticalmodelswere introduced.This paper firstly analyzed the statisticalmethod of discrete data，constructed the statisticalmodel according to the actualmeasurement RCS data in out－field of a certain tank，and performed the fitting analysis，and verified the statistical distribution rule of its RCS fluctuation.It is helpful for the study of radar target characteristics for ground equipment.

radar cross section;statisticalmodel;ground equipment

:A

1006－0707(2014)07－0013－04

form at:LIU Zeng－can，DENG Ai－ming，WANG Sen.Analysis of StatisticalModel for RCSof Tank［J］.Journal of Sichuan Ordnance，2014(7):13－16.

本文引用格式:刘增灿，邓爱明，王森.坦克目标RCS统计模型分析［J］.四川兵工学报，2014(7):13－16.

10.11809/scbgxb2014.07.005

2014－02－28

刘增灿(1979—)，男，硕士，工程师，主要从事目标特性测试与隐身技术研究。

TN971.+1