超载对RC梁桥疲劳可靠性的影响分析

刘 扬，李胜兰，邓 扬

（长沙理工大学土木与建筑学院，湖南长沙 410004）

疲劳破坏是承受车辆荷载反复作用的桥梁结构破坏的基本形式之一，进入21世纪，中国经济快速发展，交通运输迅速发展，交通量和载重量都在不断提高，超载成为常态。它将直接造成在役桥梁的损伤，削弱结构的耐久性能，不同程度地造成桥梁承载潜力降低，甚至危及桥梁的安全运营。混凝土桥梁在车辆荷载作用下，尤其是在超载和超限车辆作用下，结构发生疲劳失效的概率将显著增加。桥梁结构因疲劳荷载长期作用而导致的疲劳失效越来越显著，已经成为引发结构和构件失效的主要因素，使桥梁的疲劳研究成为桥梁工程领域的热点研究课题［1－3］。结合中国交通运输实际情况，量化车辆超载对混凝土桥梁疲劳性能的影响，并将车辆超载对桥梁结构的影响进行深入的研究，具有一定的现实意义。

基于传统的用于疲劳可靠性分析的累积损伤模型，以应力循环次数为变量，建立极限状态方程，得到疲劳可靠指标的计算公式。为了量化说明超载车辆对运营桥梁结构的疲劳可靠度影响，以某钢筋混凝土桥为背景，基于BS5400疲劳标准车模型，在此疲劳车轴重基础上增加10%和20%来界定超载，并在交通量增长条件下研究该钢筋混凝土梁桥疲劳可靠度的时变规律。

1 极限状态方程

用于疲劳可靠性分析的结构的功能函数［4］分为3类：疲劳累积损伤模型、剩余强度模型和疲劳寿命模型；因此极限状态方程有多种形式。本研究以累积损伤D（n）作为控制参数，则结构的安全余量为：

式中：D（n）为疲劳累积损伤，随疲劳荷载循环次数n单调增加；Dc为临界累积损伤。

根据式（1），结构构件的疲劳失效概率Pf为：

本研究考虑到超载情况和过桥车辆数的不断累积，选取应力的循环次数为变量，建立基于疲劳累积损伤模型下的结构极限状态方程。

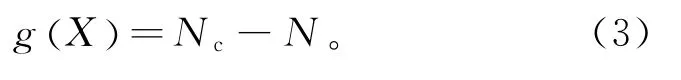
式中：Nc为结构细节在疲劳破坏的临界状态可以经历的应力循环总次数；N为结构细节已经经历的应力循环总次数。

结构的疲劳性能用S－N曲线描述，金属材料的S－N曲线表示为：NSm＝C。根据Miner线性累积损伤理论得：

式中：Se为变幅或随机应力的等效等幅应力变程。

根据Miner线性累积损伤准则，当疲劳累积损伤度D大于临界累积损伤Dc时，即发生疲劳失效，可用D≥Dc表示。Miner准则认为，对于金属结构，Dc近似等于1；式（3）和式（4）结构的极限状态方程可以化为：

2 极限状态方程各随机变量的确定

2.1 材料疲劳细节常数

将S－N曲线转变到双对数坐标体系下，有：

由于结构材料组成、构件的制作工艺和方法等因素的影响，结构的耐疲劳性能是不确定的，反映在式（7）中，材料的疲劳细节常数m和C均为随机变量。因此，在一定的应力幅作用下结构的疲劳寿命和一定的应力循环次数下结构的疲劳强度也均为随机变量。由于m的变异性很小，分析中将其视为确定性常量，仅将C作为随机变量处理。在规定的应力幅加载下，对n个结构构件进行等幅循环加载试验，可以得到在该应力幅下疲劳寿命对数均值和对数标准差［5］。

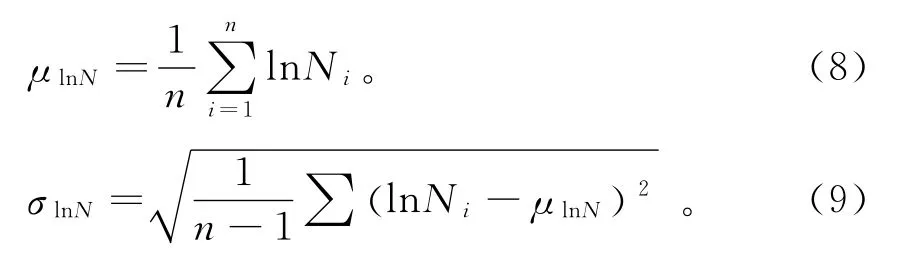
从而可以得到结构材料细节参数lnC的平均值和标准差。

材料细节常数C服从对数正态分布，对于钢筋混凝土结构中的钢筋，其疲劳性能通过对钢筋混凝土构件进行疲劳试验得到。本研究取用1991年铁道部科学研究院铁道所通过对热轧钢筋疲劳性能进行研究得到的构造细节为对接焊的20MnⅡ级钢的疲劳统计参数，见表1［6］。

表1 钢筋构造细节疲劳可靠度统计参数Table 1 Fatigue reliability statistical parameters of reinforced details

2.2 Miner线性累积损伤理论的临界损伤

Miner临界损伤Dc是由疲劳试验决定的参数，许多学者对大量的疲劳试验数据进行了统计分析，根据他们的疲劳试验数据［7－8］，发现Miner临界累积损伤Dc服从对数正态分布，均值μDc为1.0，变异系数δDc为0.3。Miner临界累积损伤Dc服从对数正态分布这一原则已经广泛应用于海洋结构和其他的工程结构中，用来计算在变幅应力谱作用下的疲劳损伤。

3 疲劳可靠度指标计算

根据极限状态方程（6），桥梁结构某细节疲劳失效时构件的失效概率为：

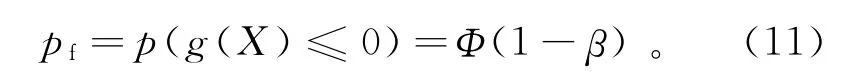
式中：β为可靠度指标；Φ（·）表示标准正态分布函数。

假定随机变量C和Dc服从对数正态分布，根据一次二阶矩法，计算可靠度指标。

式中：λDc为lnDc的均值；ζDc为lnDc的标准差；λc为lnC的均值；ζc为lnC的标准差。

由式（12）变换，得：

式中：a，b和c均为与构造细部概率统计参数和临界损伤Dc的概率统计参数有关的常量。

从式（13）可以看出可靠指标与应力幅和累积循环次数之间的关系，从而转换为超载对疲劳可靠度的影响。

4 实例分析

以跨径20m简支T梁桥为算例，进行标准疲劳车辆过桥时的应力时程分析。T型梁标准跨径为L＝20.0m，计算跨径为19.5m，设计荷载为公路II级，主筋用HRB335钢筋，其他用R235钢筋。模型尺寸如图1所示。

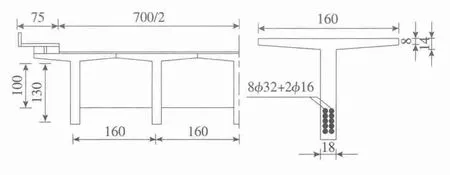
图1 简支T梁桥模型（单位：cm）Fig.1 Bridge model with simple supported T girder（unit：cm）

车辆过桥时的弯矩是恒荷载与活荷载共同作用时产生的弯矩。经计算，重车从第一车道过桥时，最不利梁为边梁，其横向分布系数最大，边梁的横向分布系数为0.319，车辆荷载作用下简支梁桥边梁的弯矩为：

目前，中国有关公路桥梁疲劳设计的相关规范滞后于国际疲劳设计理论，且缺乏针对性的疲劳设计标准车辆。对此，有些学者进行了研究。童乐为［9］等人以上海市内环线中山路3号桥地面桥为调查对象，得到了6种模型车辆；王荣辉［10］等人以广州市内环线恒福路段高架桥由东向西单行线为调查对象，根据观测结果，得到了5种典型车辆的数据等。

疲劳荷载谱在应用时很不方便，通常以对公路桥梁疲劳损伤最严重的一种型号的营运车为基础，制定标准疲劳车来代替疲劳荷载谱。本研究采用英国BS5400疲劳标准车用于疲劳可靠性评估（如图2所示），以其轴重增加10%和20%来界定超载。研究结果表明：日平均交通量ADT包括所有车型，ADTT可以用ADT乘以货车在交通量中所占的比率来确定，本研究取每日通过的疲劳标准车数目为1 000辆。

图2 英国疲劳标准车Fig.2 Fatigue vehicle of BS5400

应力历程曲线可以分解为主应力幅和较高应力幅，主应力幅是最大应力幅，剩下的是较高的应力幅。Schilling［11］在1984年证明了单辆车引起的复杂应力循环下的疲劳累积损伤可以用最大应力幅的应力循环次数Ne来替代降。其公式为：

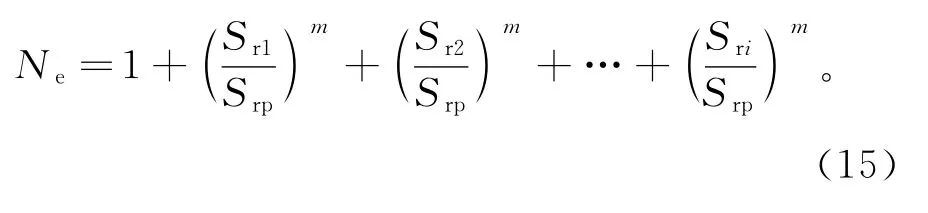
式中：m为S－N曲线的斜率，Srp为最大应力幅，Sri为较高应力幅。

采用有限元软件模拟计算模型，车辆以10m／s的速度通过该桥，得到BS5400标准疲劳车和超载车辆通过该桥时产生多于一次的应力循环，由式（15）计算得到Ne＝1.46。

表2 各超载水平下钢筋应力幅Table 2 Stress amplitude at different level of overload

中国铁路桥梁不同结构等级和极限状态的目标可靠度指标βtarget的取值［12］见表3。

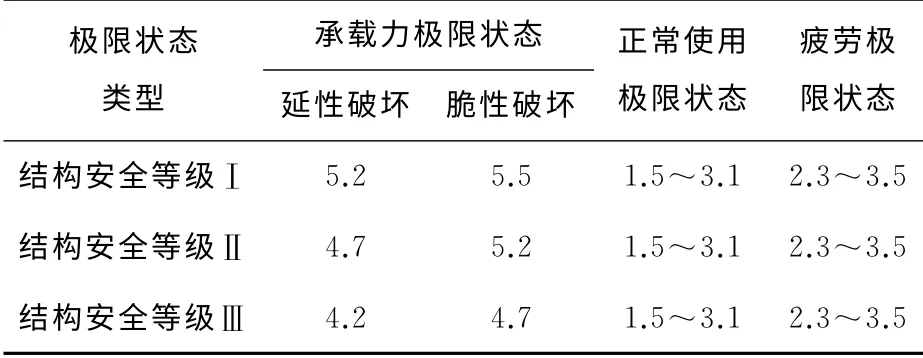
表3 中国铁路桥梁目标可靠度指标Table 3 Target reliability index of railway bridge in our country

从表3中各不同极限状态下的目标可靠度指标可以看出，由于结构一旦发生承载力失效，将会造成极为严重的生命、财产安全损失，因此承载力极限状态的目标可靠度指标取值最大，而正常使用极限状态的目标可靠度水平则相对最小。钢筋混凝土桥梁疲劳问题中，因超载问题越来越显著，而受到了公路管理部门的重视。本研究采用的目标可靠度指标βtarget＝3.5来评估钢筋混凝土桥梁的疲劳可靠性。

由式（12）计算得到的时变可靠度指标的变化曲线如图3所示。从图3中可以看出，在相同使用寿命的情况下，超载量越大，该桥的疲劳可靠度指标越低。达到目标可靠度指标βtarget的时间分别为43年、34年及26年。

图3 不同超载水平下时变可靠度Fig.3 Time－variant reliability index at different levels of vehicle overload

随着中国社会经济的不断发展，汽车保有量逐年不断增长，超载车辆也不断增多，桥梁所承受的疲劳荷载效应也会不断增长。因此，在计算服役期内桥梁的疲劳可靠度时，就必须将疲劳荷载效应的增长考虑进来［8］。考虑日循环次数增长，当日循环次数按线性增长，n年内最底层受拉钢筋所承受的应力循环总次数可表示为：

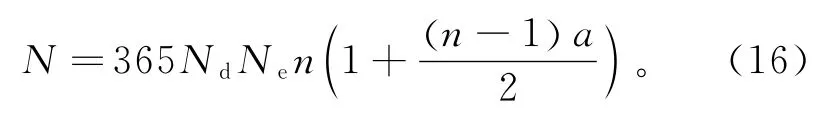
式中：Nd为日交通量（Nd＝1 000辆）；a为Nd的交通量增长系数（本研究考虑a为0%，1%和2%）。

从图4中可以看出，当考虑交通量线性增长且a分别为0%，1%和2%时，可靠度指标降低至βtarget的服役期分别为43年、37年及33年。

图4 不同交通量增长率下时变可靠度Fig.4 Time－variant reliability index with different rate of traffic growth

同时考虑超载和交通量线性增长情况下的可变可靠度变化曲线如图5所示。当同时考虑超载和交通量增长时，超载20%（a＝2%）22年、超载10%（a＝1%）29年、疲劳标准车（a＝0%）43年。

从图3，5中可以看出，同时考虑超载和交通量增长时与只考虑超载情况相比，服役后期细节的疲劳可靠度指标会急剧减小。可见，随着中国现阶段社会经济的不断发展，超载车辆不断增多，载重量也同时在不断地增长，桥梁在设计基准期内发生疲劳破坏的风险将显著增加。

图5 超载和交通量增长共同作用下时变可靠度Fig.5 Time－variant reliability index when considering overload and traffic growth

5 结论

1）随着桥梁使用寿命的增加，细节的疲劳可靠度指标逐渐降低，疲劳失效概率逐渐增大。在相同的使用寿命情况下，超载量越大，细节的疲劳可靠度指标越低，发生疲劳失效的概率相应也越大。超载20%较未超载情况下达到目标可靠指标的年限缩短了17年。

2）同时考虑超载和交通量增长将大大缩短桥梁的疲劳寿命，与只考虑超载情况相比，服役之后细节的疲劳可靠度指标会急剧减小，桥梁在设计基准期内发生疲劳破坏的风险将显著增加，超载20%且交通量按2%增长较未考虑超载和交通量增长情况下达到目标可靠指标的年限缩短的21年。

3）中国现阶段尚未有疲劳标准车模型用于桥梁的疲劳性能评估，本研究是以英国BS5400疲劳标准车作为基础的。为了对桥梁在服役期内的疲劳可靠度进行准确的预测和评估，基于中国实际交通情况，疲劳荷载谱和疲劳标准车的研究还有待进一步开展。

（References）：

［1］王春生，周江，吴全有，等.既有混凝土桥梁疲劳寿命与使用安全评估［J］.中国公路学报，2012，25（6）：101－107.（WANG Chun－sheng，ZHOU Jiang，WU Quan－you，et al.Fatigue life and service safety assessment for existing concrete bridges［J］.China Journal of Highway and Transport，2012，25（6）：101－107.（in Chinese））

［2］孙晓燕，徐冲，王海龙，等.用于疲劳可靠性分析的公路桥梁荷载效应研究［J］.公路交通科技，2011，28（5）：80－85.（SUN Xiao－yan，XU Chong，WANG Hai－long，et al.Investigation of highway bridge load effect for fatigue reliability analysis［J］.Journal of Highway and Transportation Research and Development，2011，28（5）：80－85.（in Chinese））

［3］张运波，孙立伟.车辆超载对矮塔斜拉桥可靠度影响分析［J］.铁道工程学报，2012（11）：49－53.（ZHANG Yun－bo，SUN Li－wei.Analysis of the influence of vehicle overload on the reliability of low－tower cable stayed bridge［J］.Journal of Railway Engineering Society，2012（11）：49－53.（in Chinese））

［4］李莹.公路钢桥疲劳性能及可靠性研究［D］.哈尔滨：哈尔滨工业大学，2008.（LI Ying.Research on the fatigue performance and the reliability of highway steel bridges［D］.Harbin：Harbin Institute of Technology，2008.（in Chinese））

［5］贡金鑫，赵国藩.腐蚀环境下钢筋混凝土结构疲劳可靠度的分析方法［J］.土木工程学报，2000，33（6）：50－56.（GONG Jin－xin，ZHAO Guo－fan.Fatigue reliability analysis for corroded reinforced concrete structures［J］.China Civil Engineering Journal，2000，33（6）：50－56.（in Chinese））

［6］姜海波，车惠民.既有铁路混凝土梁疲劳与承载力可靠性研究［J］.土木工程学报，2000，33（1）：27－31.（JIANG Hai－bo，CHE Hui－min.Assessment of fatigue and load－bearing reliability of existing concrete beam of a railway bridge［J］.China Civil Engineering Journal，2000，33（1）：27－31.（in Chinese））

［7］John W F，Karl H F，Manfred A H.Effect of weldments on the fatigue strength of steel beams［R］.Washington，D C：National Research Council，1970.

［8］邓扬，丁幼亮，李爱群，等.钢箱梁桥焊接细节的疲劳断裂可靠性分析［J］.工程力学，2012，29（10）：122－128.（DENG Yang，DING You－liang，LI Ai－qun，et al.Fracture fatigue reliability of welded details in bridge steel box gieders［J］.Engineering Mechanics，2012，29（10）：122－128.（in Chinese））

［9］童乐为，沈祖炎，陈忠延，等.城市道路桥梁的疲劳荷载谱［J］.土木工程学报，1997，30（5）：20－26.（TONG Le－wei，SHEN Zu－yan，CHEN Zhong－yan，et al.Fatigue load spectrum for urban load bridge［J］.Journal of Civil Engineering，1997，30（5）：20－26.（in Chinese））

［10］王荣辉，迟春，陈庆中，等.广州市高架桥疲劳荷载车辆模型研究［J］.华南理工大学学报：自然科学版，2004，32（12）：94－96.（WANG Rong－hui，CHI Chun，CHEN Qing－zhong，et al.Study on the model of the fatigue－loaded vehicles in Guangzhou trestle bridges［J］.Journal of South China University of Technology：Natural Science Edition，2004，32（12）：94－96.（in Chinese））

［11］潘际炎.铁路桥梁设计中的疲劳可靠性理论［J］.钢结构，1995，10（27）：1－10.（PAN Ji－yan.Reliability theory of fatigue in the design of railway steel bridges［J］.Steel Construction，1995，10（27）：1－10.（in Chinese））

［12］李铁夫.铁路桥梁可靠度度设计［M］.北京：中国铁道出版社.2006.（LI Tie－fu.Railway bridge reliability design［M］.Beijing：China Railway Press，2006.（in Chinese））