GRACE时变重力场滤波方法研究

姜永涛，张永志，王 帅，姚晓伟

(1.长安大学，陕西 西安 710000；2.河南工程学院，河南 郑州 451191)

GRACE时变重力场滤波方法研究

姜永涛1，2，张永志1，王 帅1，姚晓伟1

(1.长安大学，陕西 西安 710000；2.河南工程学院，河南 郑州 451191)

用3种不同的滤波方法获得了2007年相对于2005年的卫星重力变化图像，并与同期地面重力测量的结果进行比较，对比分析GRACE月重力场滤波方法的优缺点。结果表明，去相关平滑滤波算法优于高斯滤波和直接截断法，且去相关平滑滤波DDK5处理得到的卫星重力动态变化图像与地面观测结果符合最好，表明GRACE卫星时变重力场可以用来分析大区域重力动态变化。

GRACE；滤波方法；去相关滤波；高斯滤波；重力场变化

一、引 言

GRACE(gravity recovery and climate experiment)双星系统利用卫星轨道(SST-hl，GPS定轨数据)和星间距离测量数据(SST-ll，KBR星间测距数据)来解算时变重力场模型，利用这些时变重力场模型，国内外学者第一次观测到了世界范围的海水重新分布[1]、区域水储量变化[2]和大震的同震及震后重力变化[3]。由于轨道倾角约为89°，使得月重力场模型位系数之间具有相关性，且误差随阶次的增高而增大，在空间域表现为明显的南—北向条带状波纹。因此利用GRACE时变重力场数据时，首先要进行重力场位系数去相关和平滑处理。

将重力场模型截断到低阶，可以消除中高阶位系数误差对结果的影响，但同时也丢掉了中高阶位系数的重力场信息，而且截断法获得的重力场空间分辨率较低，很难用于研究较小尺度(100～300 km左右)的地球动力学现象[3]；高斯滤波法[4-5]是早期研究GRACE时变重力场常用的方法，它通过对模型高阶次位系数的降权处理来降低误差对重力场变化结果的影响；现在青睐于采用去相关并结合平滑后处理技术处理GRACE时变重力场数据，去相关处理是确定并消除模型位系数之间的相关性误差，经验分析[6-7]和先验模型[8-9]方法的去相关核都不是轴对称的形式，而是呈现出南—北向较短的旁瓣状的形状，且其大小与点坐标有关。文献[8]利用GRACE时变重力场反演过程中的信号和误差的协方差阵，基于惩罚加权的方法得到时变重力场位系数的去相关系数矩阵，但该矩阵包含的系数太多，不利于计算。GFZ[10]借鉴文献[6]简化了去相关系数矩阵，最终得到了去相关滤波方法(DDK1—DDK5)，相应的GRACE月重力场模型处理结果可在ICGEM网站上获得。

本文用3种不同的滤波方法获得了2007年相对于2005年的卫星重力变化图像，并与同期地面重力测量的结果[11]进行了比较，对比分析了GRACE月重力场滤波方法的优缺点。

二、卫星年时变重力场变化

由GRACE重力场模型得到的椭球面上的重力变化可表达为

式中，θ、λ分别为地心余纬和经度；r≈a(1－fcos2θ)，为椭球面上一点的矢径，a、f分别为参考椭球的长半轴和扁率；GM为地心引力常数；R为地球平均半径；n、m分别为模型位系数的阶和次；nm(cos θ)为完全正则化勒让德函数[12]；nm、nm为所选重力场模型相应阶次的位系数差值。

本文将2007年1—3月(冬季，可忽略区域水储量变化对重力的影响)的GRACE时变平均重力场(简称2007S)和2005年1—3月的GRACE时变平均重力场(简称2005S)进行差分计算，得到由GRACE卫星重力获得的2007年相对于2005年的重力变化图像。鉴于GRACE双星系统对位系数C20项不敏感，因此计算中视C20项为常数，并通过差分消除其影响。式(1)中取，可以得到由GRACE卫星重力场模型得到的2007年相对于2005年的差分重力场。

图1以点(34.5，105)处的重力变化为例计算了差分重力场的各阶异常大小及其标准差，可以看出差分重力场阶标准差随着阶数n的增高而增大，到90阶时，标准差可达10 μGal(1 μGal＝1×10－8m/s2)。图2为未经滤波处理的2007年相对于2005年的卫星重力场变化图像，图中可以看到明显的南—北向的条带状误差，且条纹波动可达上百μGal，因此在利用卫星重力场数据前必须进行滤波处理。

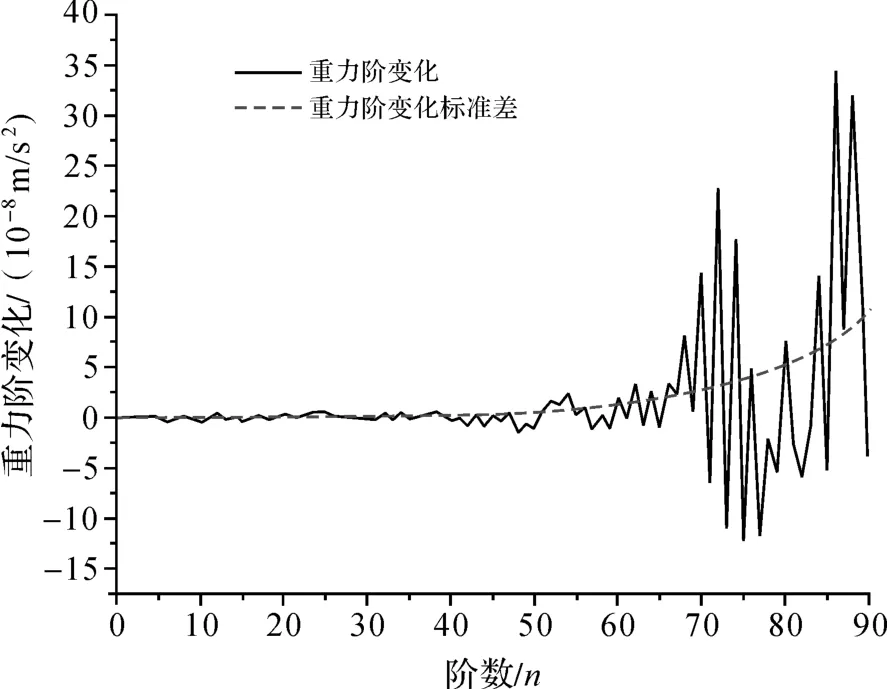
图1 重力阶变化及其标准差(单位：10－8m/s2)

图2 未经滤波处理的卫星重力变化图像(2007S—2005S，单位：10－8m/s2)

三、时变重力场滤波方法

GRACE时变重力场的常用滤波方法有高斯滤波和去相关平滑滤波。

1.高斯滤波

高斯滤波通过对重力场位系数(频率域)的加权运算来实现空间域的平滑处理，对式(1)的时变重力模型，其高斯滤波[5]可写为

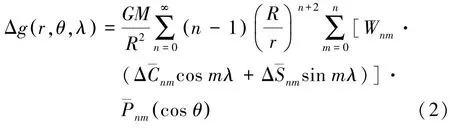
式中，Wnm为高斯权函数。各向同性高斯平滑权函数Wnm只与模型阶数有关，即Wnm＝Wn。最初的Wn是根据勒让德多项式基于分解公式给出的[13]，实用的权函数公式是将Wn作为平滑半径rfilter的函数，其递推公式为[4，14]

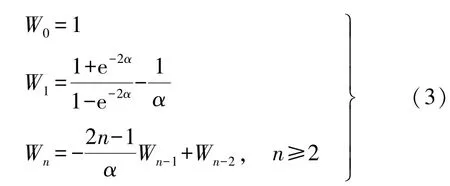
图3为各向同性高斯平滑权函数随滤波半径的变化图，可以看出各向同性高斯平滑是通过压抑高阶面谐函数的贡献(同时压制高阶项误差)来达到滤波的目的。由图3分析可知，400 km滤波半径的高斯平滑60阶以后的位系数被严重压制，且30～60阶位系数被降权处理，因此可以得到较为平滑的重力场变化结果，如图4所示。相对于未经滤波的卫星重力场变化图像(如图2所示)，图4中已不含南—北向条带误差，且量值上大为减少，其原因是400 km的各向同性高斯滤波降低了高于50阶位系数误差(如图1所示)对重力场变化的影响。

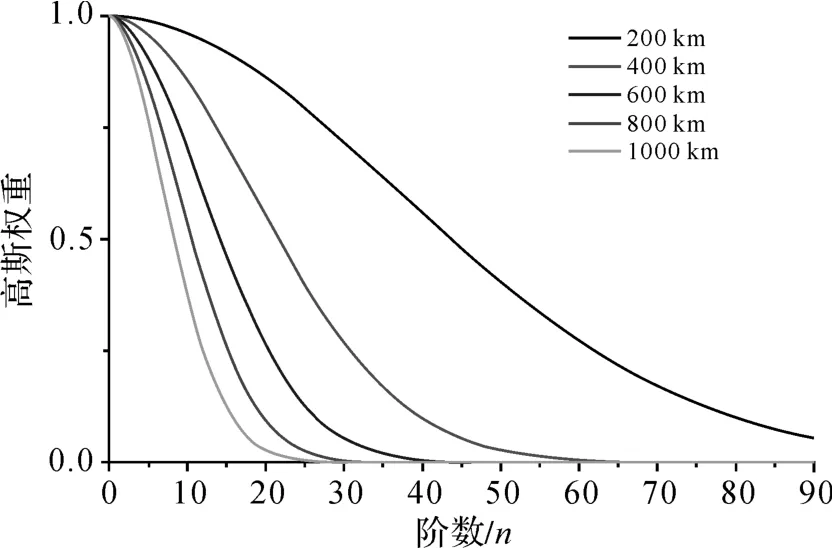
图3 不同平滑半径的各向同性高斯权函数变化

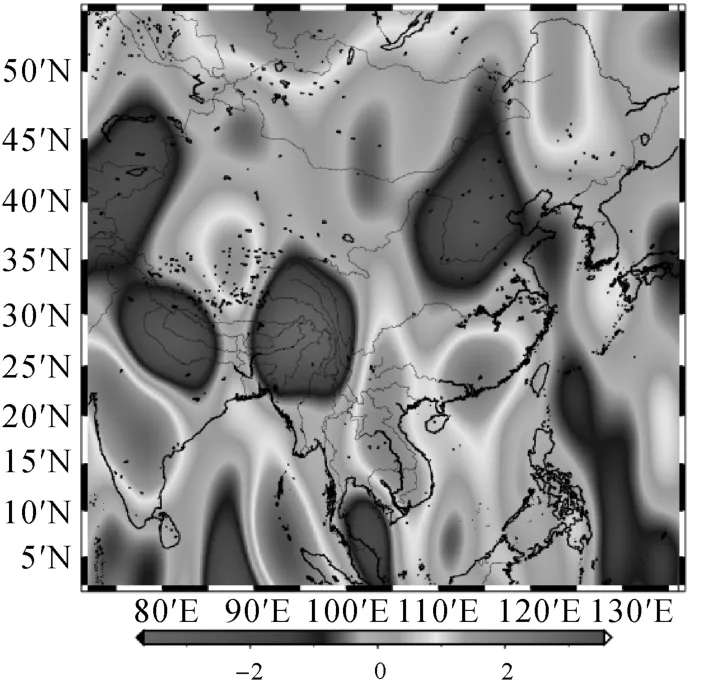
图4 各向同性高斯平滑(400 km)的重力变化图像(2007S—2005S，单位：10－8m/s2)

由于时变重力场位系数误差与其阶数n和次数m均有关，文献[5]提出各向异性高斯滤波，其递推式为

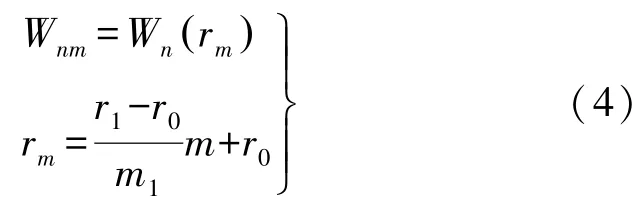
式中，r0、r1分别对应于次数为0和m1的平均滤波半径；m1为滤波截断次数。Wnm的确定与r0、r1、m1的选取有关，其中，r0决定了南—北方向上的平滑半径；r1、m1决定了在东—西方向上的平滑半径。因此通过选取合适的各向异性高斯滤波参数，可以提高时变重力场在南—北向的分辨率。

本文试算了不同r0、r1、m1参数得到的时变重力场图像，并从条纹消除和变化细节保留两方面分析得出r1＝400 km，r0＝200 km，m1＝60的结果最佳，如图5所示。图6给出了上述r1、r0、m1取值下的各向异性高斯滤波权系数，可以看出各向异性高斯滤波同阶的权函数不再相同，且考虑了模型高阶低次(m＞m1)的位系数对时变重力异常的贡献。由于r0＝200 km，图5相比于各向同性高斯平滑(如图4所示)，在南—北方向上更凸显了细节，且量值上略大于400 km平滑半径的各向同性高斯滤波结果。

2.去相关平滑滤波

去相关平滑滤波(DDK1—DDK5)是GFZ根据Kusche[8]和Swenson等人[6]的研究得出的一个卷积矩阵较为简单的去相关平滑方法。不同于高斯滤波，去相关平滑滤波(DDK1—DDK5)考虑了由GRACE轨道数据和星间距离测量数据反演月重力场模型过程中产生的信号协方差和误差协方差矩阵，通过惩罚加权法构建去相关系数矩阵，又针对去相关滤波矩阵系数的特点[6]，发展出的一个“次卷积”去相关滤波核。位系数的滤波结果可表示为

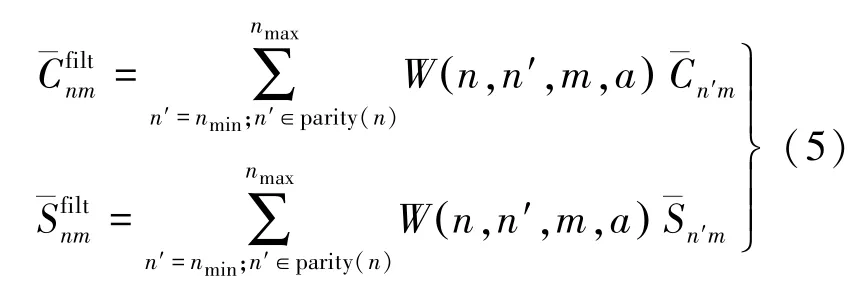
式中，W( n，n′，m，a)为去相关滤波核；a决定平滑程度；n′∈parity(n)表示n′与n的奇偶性相同；n′m、n′m为未经滤波的时变重力场位系数。由式(5)可以看出，滤波后的某一阶次的位系数可由与该位系数同次不同阶的位系数的加权求和，即“次卷积运算”获得。

图5 各向异性高斯平滑(400 km，200 km，60)的重力变化图像(2007S—2005S，单位：10－8m/s2)

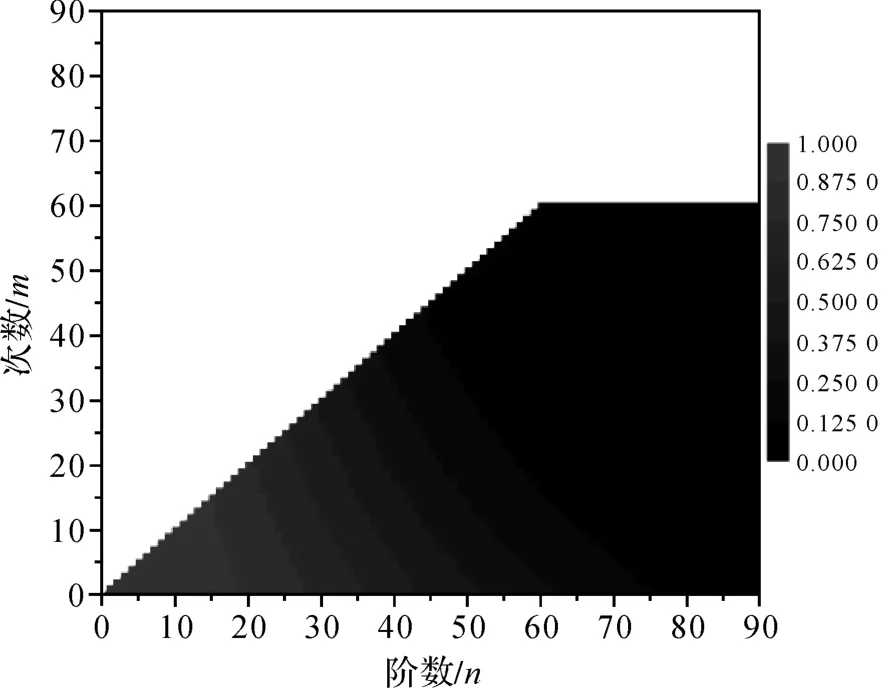
图6 各向异性高斯平滑(400 km，200 km，60)的各阶次权系数

GFZ去相关核W( n，n′，m，a)是通过矩阵的方式提供的，此外经过DDK滤波处理的时变重力场数据可从ICGEM网站下载。图7为2007年相对于2005年的卫星重力场变化DDK3滤波结果，可以看出，去相关滤波不仅消除了条带误差，且量值上较高斯滤波结果大，说明DDK3滤波较有效地保留了时变重力场的高阶次信息。

图7 去相关滤波DDK3处理的重力变化图像(2007S—2005S，单位：10－8m/s2)

四、时变重力场处理方案

文献[11]给出了由中国大陆地壳运动网络、中国数字地震观测网络的重力网流动观测成果得出的2007年相对于2005年中国大陆动态重力场变化图像。本节参照同期地面重力测量的结果(文献[11])来对比分析GRACE月重力场滤波方法的优缺点。

对于各向同性高斯滤波，通过试算，滤波半径400 km的各向同性高斯平滑得到的结果最优，如图4所示。由图3中不同滤波半径的高斯权系数可知，400 km的高斯平滑已经完全压制了60阶以后的位系数，且使得30～60阶位系数的贡献值低于30%，因此虽然在量级上图4小于直接截断结果(如图8所示)，但在时变重力场细节上，400 km各向同性高斯平滑优于直接截断法，且与地面重力测量得到的动态变化图像(文献[11])高值区和低值区的对应性上更好些。

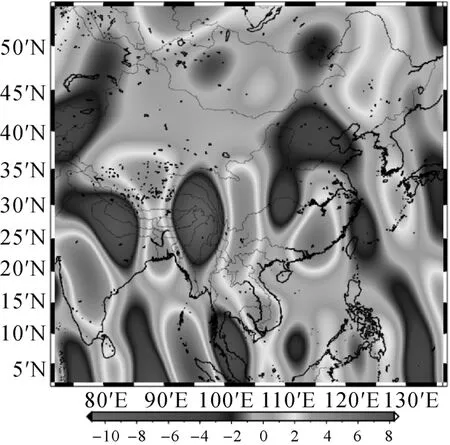
图8 截断36阶得到的重力变化图像(2007S—2005S，单位：10－8m/s2)

对于各向异性高斯滤波，试算发现r1＝400 km，r0＝200 km，m1＝60时结果最优，如图6所示。综合比较图6、图4和图8的重力场变化高、低值区可以发现，相对同性高斯滤波，各向异性高斯滤波确实提高了南—北方向上的重力场变化分辨率，但实际意义两者没有大的差异。

利用ICGEM提供的DDK1—DDK5月重力场模型数据计算了2007S相对于2005S的年重力场变化，结果表明，DDK3—DDK5的结果与文献[11]的空间对应较好，原因是DDK1—DDK2处理的重力场等效平滑半径较大，平滑了重力变化细节。通过与文献[11]比较可知，DDK5处理卫星重力场变化结果(如图9所示)最优。

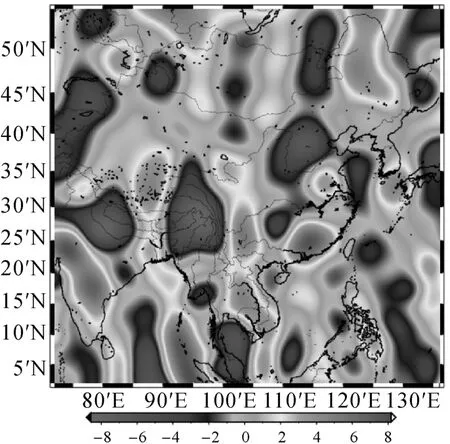
图9 去相关滤波DDK5处理的重力变化图像(2007S—2005S，单位：10－8m/s2)

五、结 论

本文利用GRACE卫星时变重力数据，采用不同的滤波方法计算了2007年相对于2005年的卫星重力动态变化图像，通过与地面重力测量结果的对比分析，得出如下结论：

1)去相关平滑滤波算法优于高斯滤波和直接截断法。直接截断法删除了中高阶项重力场信息，降低了空间分辨率；高斯滤波法随阶数增高而降低的权函数在一定程度上减少了最终结果的量值；去相关滤波由于其滤波核的获取具有一定的物理意义，因此得到了相对较好的处理结果。

2)各种滤波方法得到的卫星重力场变化的高、低值区空间分布与地面重力观测结果具有较好的一致性，但量值上均相差约一个量级。高、低值区客观上的良好对应关系表明GRACE时变重力数据可以较好地应用在地学研究中。

本文得到的结论对水文学和地学相关研究中选定时变重力场滤波方法有一定的参考作用。

[1] CHAMBERS D，WAHR J，NEREM R S.Preliminary Observations of Global Ocean Mass Variations with GRACE[J].Geophysical Research Letters，2004，33 (13).DOI：10.1029/2004GL020461.

[2] SCHMIDT R，SCHWINTZER P，FLECHTER F，et al. GRACE Observations of Changes in Continental Water Storage[J].Global and Planetary Change，2006，50(1-2)：112-126.

[3] HAN S C，SIMONS F J.Spatiospectral Localization of Global Geopotential Fields from the Gravity Recovery and Climate Experiment(GRACE)Reveals the Coseismic Gravity Change Owing to the 2004 Sumatra-Andaman Earthquake[J].Journal of Geophysical Research：Solid Earth，2008，113(B1)：B01405.DOI：10.1029/ 2007JB004927.

[4] WAHR J，MOLENAAR F，BRYAN F.Time Variability of the Earth’s Gravity Field：Hydrological and Oceanic Effects and Their Possible Detection Using GRACE[J]. Journal of Geophysical.Research：Solid Earth，1998， 103(B12)：30205-30229.

[5] HAN Shin-Chan，SHUM C K，JEKELI C，et al.Non-isotropic Filtering of GRACE Temporal Gravity for Geophysical Signal Enhancement[J].Geophysical Journal International，2005，163(1)：18-25.

[6] SWENSON S，WAHR J.Post-processing Removal of Correlated Errors in GRACE Data[J].Geophysical Research Letters，2006，33(8)：L08402.DOI：10.1029/ 2005GL025285.

[7] WOUTERS B，SCHRAMA E J O.Improved Accuracy of GRACE Gravity Solutions through Empirical Orthogonal Function Filtering of Spherical Harmonics[J].Geophysical Research Letters，2007，34(23)：L23711.DOI：10. 1029/2007GL032098.

[8] KUSCHE J.Approximate Decorrelation and Non-isotropic Smoothing of Time-variable GRACE-type Gravity Field Models[J].Journal of Geodesy，2007，81(11)：733-749.DOI：10.1007/s00190-007-01433.

[9] KLEES R，REVTOVA E A，GUNTER B，et al.The Design of an Optimal Filter for Monthly GRACE Gravity Models[J].Geophysical Journal International，2008，175 (2)：417-432.DOI：10.1011/j.1365-246X.2008.03922. x.

[10] KUSCHE J，SCHMIDT R，PETROVIC S，et al.Decorrelated GRACE Time-variable Gravity Solutions by GFZ，and Their Validation Using a Hydrological Model[J]. Journal of Geodesy，2009，83(10)：903-913.DOI：10. 1007/s00190-009-0308-3.

[11] 李辉，申重阳，孙少安，等.中国大陆近期重力场动态变化图像[J].大地测量与地球动力学，2009，29(3)：1-10.

[12] HOLMES S A，FEATHERSTONE W E.A Unified Approach to the Clenshaw Summation and the Recursive Computation of Very High Degree and Order Normalised Associated Legendre Functions[J].Journal of Geodesy，2002，76(5)：279-299.

[13] HOBSON E W.The Theory of Spherical and Ellipsoidal Harmonics[M].New York：Chelsea Publishing Company，2012.

[14] JEKELI C.Alternative Methods to Smooth the Earth’s Gravity Field[R].Ohio：Ohio State University，1981.

Study on Filtering Methods of GRACE Temporal Gravity Variation

JIANG Yongtao，ZHANG Yongzhi，WANG Shuai，YAO Xiaowei

P223

B

0494-0911(2014)11-0001-05

2013-09-12；

2014-08-29

国家自然科学基金(41374028；41274083；41304013)；国土资源大调查项目(1212010914015)

姜永涛(1985—)，男，山东菏泽人，博士生，主要研究方向为卫星重力。

姜永涛，张永志，王帅，等.GRACE时变重力场滤波方法研究[J].测绘通报，2014(11)：1-5.

10.13474/j.cnki.11-2246.2014. 0350