地理国情要素时空变化检测技术研究

王 怀，高小明，樊文峰，何昭宁

(国家测绘地理信息局卫星测绘应用中心，北京 101300)

地理国情要素时空变化检测技术研究

王 怀，高小明，樊文峰，何昭宁

(国家测绘地理信息局卫星测绘应用中心，北京 101300)

面向地理国情要素变化提出了一种几何匹配相似度的变化检测方法，并将该方法运用到点、线、面三种几何类型的地理要素变化检测中。针对变化检测结果设计了一种版本-差量的时空数据库模型来存储地理要素变化检测结果，以揭示地理要素的时空特征及其变化趋势。

地理要素；变化检测；版本-差量

一、引 言

在地理信息系统中，既需要对数据进行实时更新，也要对历史数据进行分析，对未来变化趋势作出预测[1]。时空数据的变化检测[2]就显得尤为重要，主要包括栅格时空数据变化检测和矢量时空数据变化检测。近几年来，对基于遥感影像的变化检测技术已经取得可观的成就，基于矢量时空数据的变化检测分析逐渐成为国内外许多科研机构和学者研究的重要内容。

从时间角度看，时态地理信息系统[3]中空间信息可分为两种类型，即动态的和静态的。现实世界中绝大多数现象本质上都是动态的，静态信息是描述在较短时间内没有变化的空间对象的信息，如地质图、道路、公共设施等，但在长期的一段时间里，这些对象都会发生变化。动态信息是描述在较短时间内发生了变化的空间对象的信息，时间的长度依不同的领域而定。时空变化是地理实体及其属性在时间轴上的改变过程。对时空变化进行分类，有助于对时空变化分析的理解，对时空数据库模型[4-5]的建立和时空变化检测也有一定的帮助。分类原则的不同，时空变化描述的重点将会有很大的差异。根据研究领域的不同，时空对象的变化可概括为：要素随时间的几何变化、要素随时间的位置变化、要素属性随时间的变化。

地理国情[6]监测是近年来国家提出的重要战略规划，地理国情是重要的基本国情，是国土疆域面积、地理区域划分、地形地貌特征、道路交通网络、江河湖海分布、土地利用与土地覆盖、城市布局和城镇化扩张、生产力空间布局等自然和人文地理要素的宏观性、整体性、综合性体现。地理国情要素的变化检测研究主要集中于地理实体匹配、图像配准、地图合并技术及其相关变化分析应用领域。本文主要研究矢量地理要素实体[7]变化检测技术实现以及变化结果的增量模式存储。

二、地理要素变化检测方法

地理要素数据变化检测首先是确定变化检测数据的候选集。如何在候选集中快速找出待匹配候选集[8]，对空间数据变化检测效率有重要影响。而匹配候选集的确定需要通过空间搜索来实现，空间搜索一般包含按空间位置的搜索、空间关系的搜索等。空间搜索一般借助于空间索引机制在空间数据库中搜索符合查询条件的空间实体，常用的空间搜索方式有基于空间索引机制的搜索、基于空间拓扑关系的搜索[9]。

矢量地理要素的变化检测主要体现在点要素、线要素以及面要素的变化检测方面。而变化检测主要体现在地理要素的几何匹配，从空间形状的角度出发，对地理要素的几何形状作定量和定性的分析，比较其间的相似程度来找同名实体[10]。本文中点要素匹配采用欧氏距离匹配，线要素匹配采用Hausdorff距离[11]匹配，面要素匹配采用Hausdorff距离、质心点距离、面积重叠度等3个特征匹配。

1)点要素匹配采用欧氏距离

在点要素的匹配中是常用的匹配方法，计算点与点之间的欧氏距离便可实现点要素的匹配过程。

点要素匹配中欧氏距离以参考点要素实体为圆心，以匹配阈值为半径做缓冲区，遍历候选集中所有待匹配目标实体。

2)线要素的匹配采用Hausdorff距离，是对两组点集相似程度的一种量度，是对两组点集之间距离进行定义的一种形式，一般适用于线与线、面与面要素之间距离相似度的计算。假设有两组点集A、B，其中A＝{a1，a2，…，an}，B＝{b1，b2，…，bm}，则A到B的Hausdorff距离与B到A的Hausdorff距离定义为

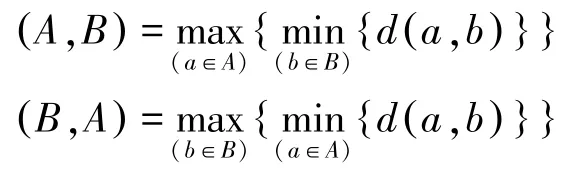
其中，d( a，b)为A、B两点集之间的距离；A、B之间的Hausdorff距离定义为h(A，B)、h(B，A)中的最大值

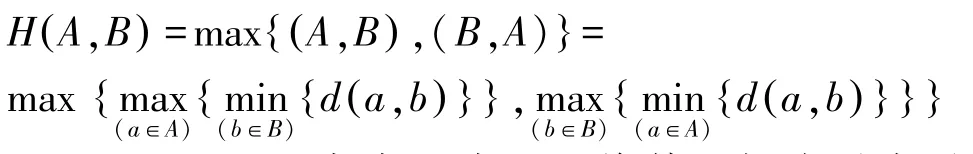
Hausdorff距离表达式可以将其理解为最大最小距离，对于任意两条线L1、L2，L1到L2的hausdorff距离为d1，L2到L1的hausdorff距离为d2，d1、d2分别是圆心在L1、L2上滚动圆的最大半径。

3)由于面要素的空间复杂程度较高，在面要素匹配过程中，依靠单一的几何特征进行匹配往往难以准确做出判断。基于面要素的空间复杂性，本文通过计算特征相似度来比较两面要素空间实体之间的各种差异，并对各相似度加权平均来获得总相似度值，面要素匹配主要考虑Hausdorff距离、质心点距离、面积重叠度等几个方面的因素。

对于参考要素A在候选集B中，共有n个要素比较，A、B总相似度为sim(A，B)，其中：si为相似特征；ωi为权重。

①Hausdorff距离

设面要素A、B之间Hausdorff距离为H( A，B)，则A、B的Hausdorff距离相似度为

其中，rA、rB分别为面要素A、B最小外接矩形(MBR)对角线长的一半，由于不规则多边形的半径难以确定，因此引入rA＋rB来反映多边形的尺寸，由于rA＋rB是基于图形本身的相对值，不受位置与尺寸的影响，用作相似度值计算常量具有一定的合理性。

②质心距离

设面要素A、B质心之间距离为Dist(A，B)，则A、B质心距离相似度为

③重叠度

设面要素A、B的面积分别为SA、SB，二者重叠相交面积为SA∩B，则A、B重叠相似度为

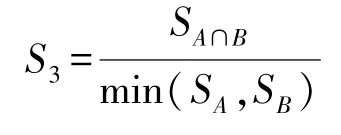
三、版本-差量时空数据模型

基于“版本-差量[12]”式时空数据模型的时空数据变化检测结果是增量式存储，本文采用建立现势库、过程库等逻辑库来存储动态数据。现势库存储现势数据，在时空数据库系统中将作为整个数据集的基态；过程库跟踪地理要素演变的各个阶段，描述地理要素演变的全过程，记录地理实体的亲缘关系，能很好地支持地理要素的时空回溯，对于任意给定的时刻或时间段，都可从过程库中查询出地理要素历史的状态，恢复当时对象的时空关系。

采用“版本-差量”时空数据库模型的实现技术，将动态数据以增量存储方式进行存储，时空数据存储在于解决时间序列的空间数据存储，由于空间数据在时间序列的演变过程中，大量空间要素信息变化较少或没有变化，采用差量式时空数据存储方案，只存储发生变化的时空数据，未发生变化或未发现变化的时空数据不存储。本文设计表1—表5来实现“版本-差量”数据模型存储。

其中，表1、表2是维护数据版本数据库结构表；表3是地理要素基态表；表4是地理要素消失的记录表；表5是地理要素发生变化时，前一时态和后一时态的关系记录表。

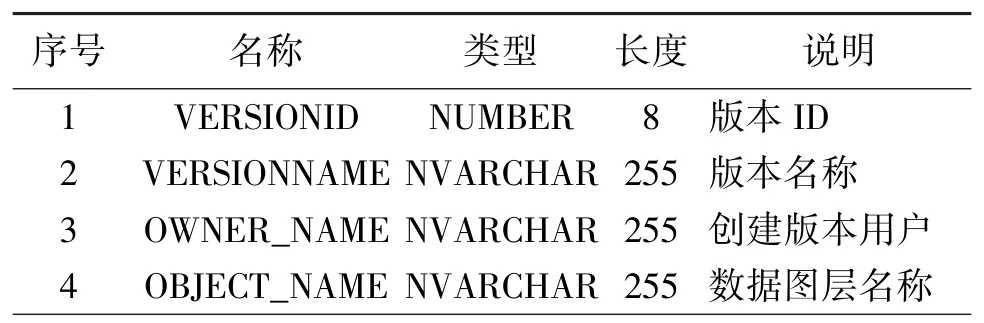
表1 数据版本

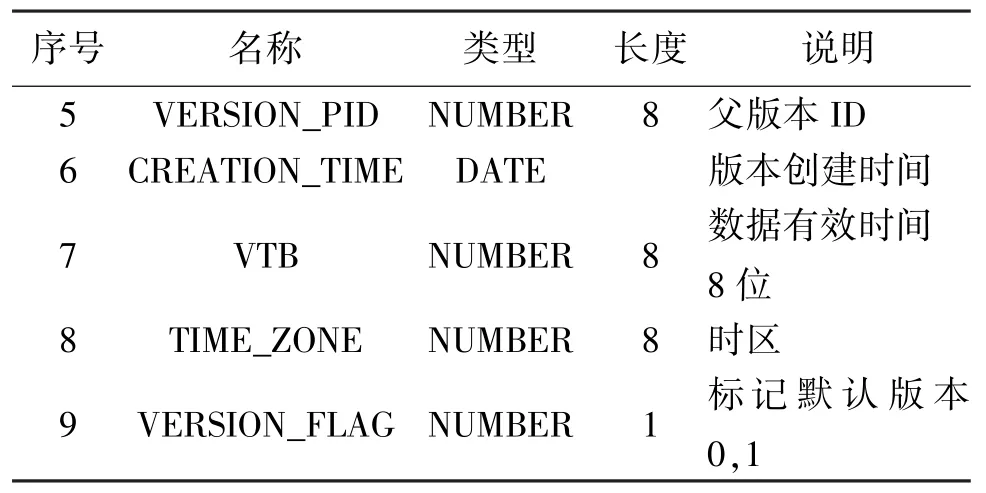
序号名称类型长度说明5VERSION_PIDNUMBER8父版本ID 6CREATION_TIMEDATE版本创建时间7VTBNUMBER8数据有效时间8位8TIME_ZONENUMBER8时区9VERSION_FLAGNUMBER1标记默认版本0，1

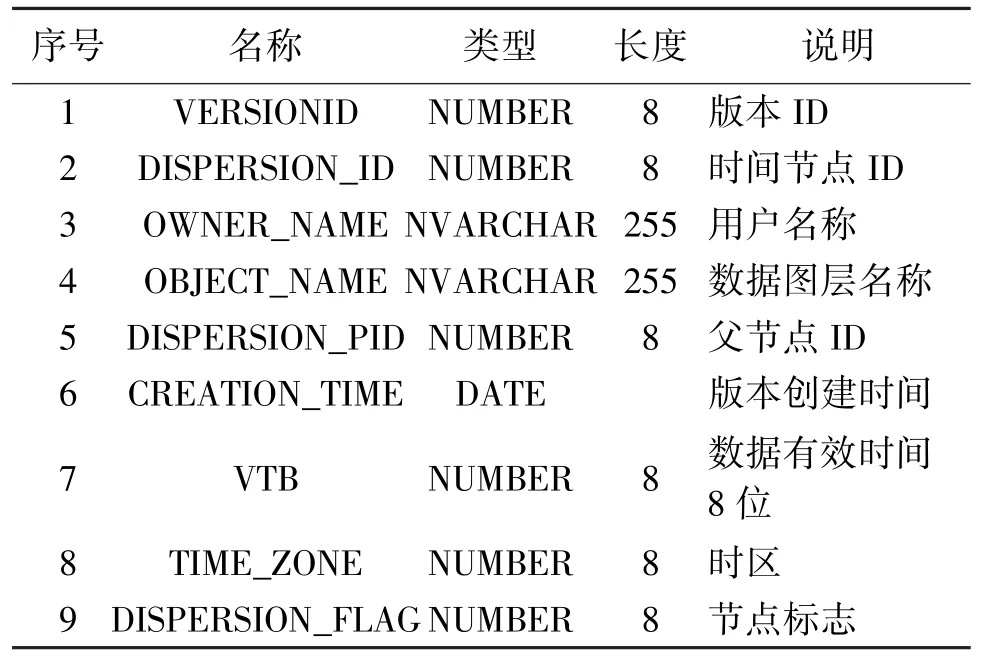
表2 版本时间节点

表3 数据基态表

表4 数据基态D表

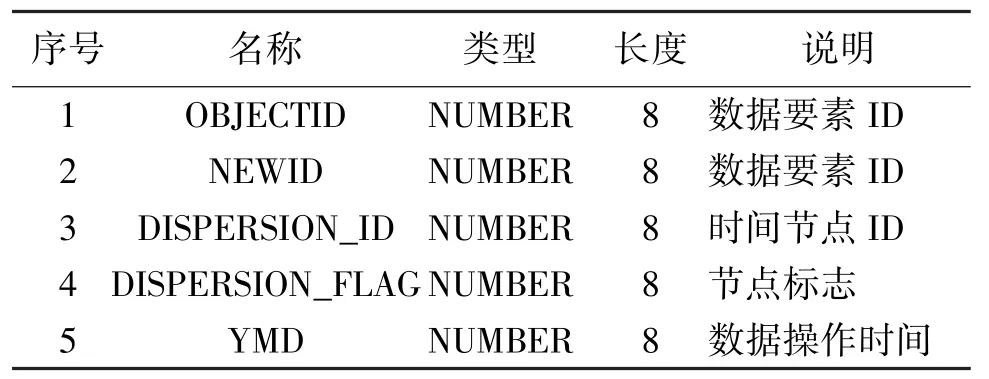
表5 数据基态R表

四、地理要素变化检测流程

本文针对上述点、线、面要素的几何变化检测研究，设计了以下变化检测流程如图1所示。

图1 地理要素变化检测流程

1.数据预处理

由于数据获取来源的不同，使得同一地区的数据在数据存储格式、坐标系统及投影系统、数据精度等方面存在差异。因此，在进行地理要素变化检测之前要进行数据预处理，形成变化检测前的基态时空数据。其他待变化检测时态的数据的数据格式、坐标系统、数据进度统一到基态数据上。

2.数据变化检测

根据上面阐述的检测算法，进行地理要素变化检测。

点要素变化检测，以参考点要素实体为圆心，以匹配阈值为半径做缓冲区，遍历所有待匹配目标实体，点要素匹配过程中距离阈值的设置应根据实际数据而定，若设置范围太大，可能出现一点对较多点的匹配；若设置范围太小，可能找不到同名点。一般地匹配阈值设定有两种方式[13]：

1)在地图点位精度已知的情况下，匹配阈值可设为精度的若干倍数，设两图幅精度分别为p1、p2，按误差传播定律两同名点的距离精度此时两图幅的匹配阈值可设为p的倍数，如2倍的p等。

2)在地图点位精度未知情况下，匹配阈值由人工统计方式确定。具体方法是在两图幅上人工寻找同名点，统计若干同名点的距离差异，依据统计值给出一个匹配阈值(如平均值、中值等)。

线要素变化检测主要是两种方法：一是用Hausdorff距离来比较两线要素的总体差异；二是用节点到曲线的距离来计算线要素的细节差异，然后对二者差异取加权平均值。变化检测步骤如下：

1)对新时态数据集A中线要素依据其MBR建立R树索引RA。

2)遍历旧时态数据集B中每个线要素b，在RA中查找与b的MBR相交的所有线要素作为b的匹配候选集A′。

3)若A′中没有元素，转第2)步。

4)遍历A′中元素a′，对b与a′分别作Hausdorff距离匹配和改进的结点距离相似度计算，根据给定的权值对两种匹配结果加权求和得总相似度值Sim(b，a′)。若A′中元素全部遍历，转第2)步。

5)若Sim(b，a′)大于等于给定的阈值ε，设b、a′的长度分别为len(b)、len(a′)，

若len(b)＞len(a′)，记录b与a′变化关系为缩小；

若len(b)＜len(a′)，记录b与a′变化关系为扩大；

若len(b)＝len(a′)，记录b与a′变化关系为无变化。

6)若Sim(b，a′)小于给定的阈值ε，转到第4)步。

7)重复步骤2)—6)，得到A、B两要素集变化关系，算法结束。

面要素变化检测采用上述Hausdorff距离、质心点距离、面积重叠度等3个方面的因素，其变化检测步骤如下：

1)对新时态数据集A中线要素依据其MBR建立R树索引RA。

2)遍历旧时态数据集B中每个线要素b，在RA中查找与b的MBR相交的所有面要素作为b的匹配候选集A′。

3)若A′中没有元素，转第2)步。

4)遍历A′中元素a′，对b与a′按第1)步计算总相似度Sim(b，a′)，根据给定的权值对两种匹配结果加权求和得总相似度值Sim。若A′中元素全部遍历，转到第2)步。

5)若Sim(b，a′)大于等于给定的阈值ε，且S3＝1，设b、a′的面积分别为Area(b)、Area(a′)，

若Area(b)＞Area(a′)，记录b与a′变化关系为缩小；

若Area(b)＜Area(a′)，记录b与a′变化关系为扩大；

若Area(b)＝Area(a′)，记录b与a′变化关系为无变化。

6)若Sim(b，a′)小于给定的阈值ε，转到第4)步。

7)重复步骤2)—6)，得到面要素变化关系。

3.变化检测的结果存储

设计基于“版本-差量”式时空数据模型的增量数据存储，把变化检测的结果存储到数据库中，与基态数据形成时空数据库。

五、结束语

地理要素时空数据变化检测技术对所有与地理信息有关的领域有广泛的应用前景，特别是对经常性变化的空间信息的管理具有重要的意义。在地理国情方面，通过对地理国情要素的变化检测的结果统计和对比分析，揭示监测对象的变化演进规律，并对监测对象未来的发展演化方向进行分析，预测所形成的趋势信息，如城市化、草地退化、沙漠化及其他重要地理要素变化趋势等信息。在基础地理信息数据管理方面，时空数据变化检测技术在基础地理信息管理中也有着很大的应用前景。各级测绘部门在更新过程中，可以基于基态版本的数据之上，利用现势数据对其进行变化检测，形成增量式的基础地理数据，构建基础地理信息数据的多时态数据。采用时空数据增量存储模式，使得历史数据与现势数据融合在一起，充分发挥历史数据的作用，从而更加便于对地理信息进行地理变迁、地理现象变化规律等的分析研究。

[1] 刘刚，周炳俊，安铭刚，等.时态GIS理论及其数据模型初探[J].北京测绘，2008(4)：16-20.

[2] 张振龙，曾志远，李硕，等.遥感变化检测方法研究综述[J].遥感信息，2006(5)：64-66.

[3] 汪汇兵，唐新明，史绍雨，等.一种基于时态树结构的时空数据的动态可视化方法[J].测绘科学，2009，34(1)：110-112.

[4] 唐新明，吴岚.时空数据库模型和时间地理信息系统框架[J].遥感信息，1999(1)：4-8.

[5] 田娇娇，唐新明，杨平，等.动态数据库模型的研究与应用[J].测绘科学，2006，31(1)：123-124.

[6] 陈俊勇.地理国情监测的学习札记[J].测绘学报，2012，41(5)：633-635.

[7] 陈爱军，李琦，徐光祐.地理空间信息共享理论基础及其解决方案[J].清华大学学报：自然科学版，2002，42(10)：1405-1409.

[8] 翟仁健.基于全局一致性评价的多尺度矢量空间数据匹配方法研究[D].郑州：解放军信息工程大学，2011.

[9] 徐文祥.基于空间特征码的矢量要素变化检测研究[D].南京：南京师范大学，2011.

[10] 郭黎，崔铁军，王豪，等.基于面状要素拓扑关系的数据匹配技术研究[J].测绘科学，2010(1)：130-132.

[11] 王文成，李晓伟，智佳，等.基于Hausdorff距离的轮廓线匹配[J].西安邮电学院学报，2007，12(3)：91-94.

[12] 汪汇兵，唐新明，洪志刚.版本差量式时空数据模型研究[J].测绘科学，2006，31(5)：131-133.

[13] 郭黎.多源地理空间矢量数据融合理论与方法研究[J].郑州：解放军信息工程大学，2008.

Study on the Geographical Situation Elements Spatio-temporal Change Detection Technique

WANG Huai，GAO Xiaoming，FAN Wenfeng，HE Zhaoning

P208

B

0494-0911(2014)11-0084-04

2014-06-11

江苏省测绘科研项目(JSCHKY201313)

王 怀(1975—)，男，四川温江人，硕士，助理研究员，现主要从事地理信息系统数据的时空建库、影像数据建库、三维GIS虚拟仿真方面的应用研究工作。

王怀，高小明，樊文峰，等.地理国情要素时空变化检测技术研究[J].测绘通报，2014(11)：84-87.

10.13474/j.cnki.11-2246.2014. 0370