悬架液压衬套液固耦合有限元分析

秦 民，蒋永峰，马天飞，刘亚川，张敏敏

(1.中国第一汽车股份有限公司技术中心，长春 130012; 2.吉林大学汽车仿真与控制国家重点实验室，长春 130022)

悬架液压衬套液固耦合有限元分析

秦 民1，蒋永峰1，马天飞2，刘亚川2，张敏敏2

(1.中国第一汽车股份有限公司技术中心，长春 130012; 2.吉林大学汽车仿真与控制国家重点实验室，长春 130022)

液压衬套作为汽车悬架系统的重要隔振元件，其静、动特性分析和隔振性能匹配在其研究开发中具有重要意义。利用液固耦合有限元方法对液压衬套进行建模分析，通过静态和动态仿真与试验的对比验证了模型的正确性。仿真计算衬套关键参数，为后期的试验和参数化分析提供指导，并利用该方法对参数化分析结果进行了结构验证。

液压衬套;液固耦合;有限元分析

液压衬套作为悬架控制臂与车身之间的连接件和隔振件，通过在橡胶衬套基础上封装液体，使其能在较广的频率范围内提供大阻尼［1］，因此在中高级乘用车悬架系统中得到广泛应用。研究液压衬套动态特性对改善悬架振动性能具有重要意义。

作为液压隔振元件，液压衬套和液压悬置有诸多相似之处，因此在对液压衬套的研究中大多借鉴液压悬置的研究方法。上官文斌［2］建立了橡胶悬置的液固耦合有限元模型，通过仿真计算对静、动特性、液室与惯性通道的压力分布、惯性通道中液体流速分布等进行了研究，提出在对悬置低频动特性进行仿真时，应用液固耦合有限元方法可得到比集总参数模型更好的结果。史文库等［3－4］运用有限元与试验相结合的方法对某轻型卡车驾驶室液压悬置进行了性能匹配，研究了悬置各参数对其动特性的影响规律。潘孝勇［5］建立了基于网格叠加橡胶隔振器黏弹塑性材料模型，并将其应用于液压衬套液固耦合分析中。Gil－Negrete［6］对利用ABAQUS建立的橡胶主簧结构模型和FLUENT建立的液体模型进行联合仿真分析，预测了液压衬套的动态特性。Karlsson等［7］利用试验获取模型参数，根据橡胶衬套的频率相关性及振幅相关性的特性建立液压衬套的橡胶部分模型。

本文利用计算流体力学和有限元相结合的方法对某汽车悬架液压衬套进行建模和仿真分析，通过试验验证了模型正确性，并利用该模型计算液压衬套关键物理参数，最后利用有限元模型对液压衬套AMESim参数化模型优化方案进行了仿真验证。

1 液压衬套结构和原理

本文研究的径向式液压衬套结构如图1(a)所示，安装在某乘用车下控制臂和副车架相连的部位，用于减少振动的传递，改善乘坐舒适性。液压衬套三维几何模型如图1(b)所示。

液压衬套的金属内套与橡胶主簧内表面硫化为一体，用于连接副车架;尼龙限位块与金属内套固结，防止载荷过大破坏衬套;橡胶主簧是承载和减振的重要部分;对称布置的2个液室通过斜的惯性通道相连;金属外套与金属骨架过盈配合(之间添加橡胶密封环)，将油液(乙二醇水溶液)密封在液室中，并连接悬架下控制臂。

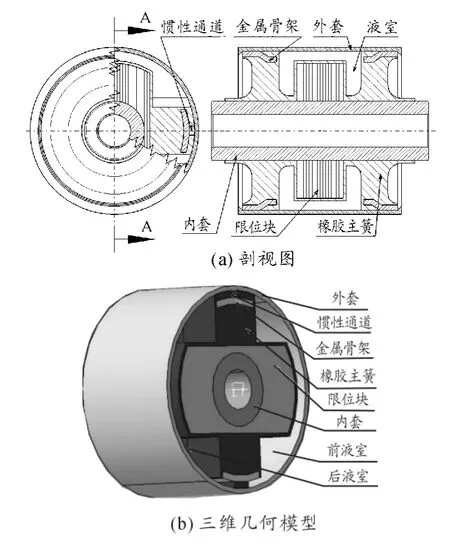
图1 液压衬套结构

当液压衬套的金属内、外套在液室方向发生径向相对位移时，一个液室受压缩变小，而另一液室受拉伸变大，油液通过惯性通道在两液室中不断地来回流动。液体通过惯性通道时出现能量损失(沿程损失、摩擦损失等)，从而产生较大阻尼，实现快速减振。当通道中的液柱产生共振时，能量损失消耗最快，相应的阻尼滞后角也会达到最大值［2］。这时其阻尼滞后角可达到传统橡胶衬套的8～10倍［5］。在更高的频率其阻尼滞后角将下降。

2 建立液压衬套的液固耦合有限元模型

2.1 液压衬套固体有限元建模

1)固体网格的划分。将液压衬套三维几何模型导入前处理软件HyperMesh中进行适当的几何清理，如将不关注的倒角删除等。金属外套固定在下控制臂孔中，刚度很大，在有限元模型中可以省略。然后对衬套固体部分的各个零件分别进行体单元划分，得到液压衬套固体有限元网格模型，如图2所示。模型共有23 362个体单元，其中22 406个8节点六面体单元，956个6节点五面体单元。金属内套与限位块之间的粘结、各金属件与橡胶主簧之间的硫化都用节点拟合来模拟［8］。

图2 液压衬套固体有限元网格模型

2)各零件材料属性的确定。考虑到橡胶主簧的非线性特性(滞后角一般在3°～5°)远小于液压衬套整体非线性特性，为了缩短模型计算时间，对其进行线性化处理。各零件材料属性如表1所示。

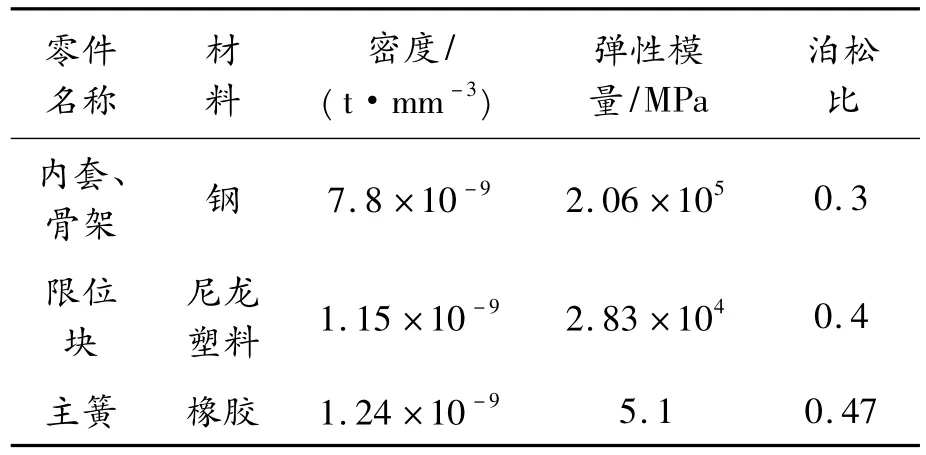
表1 材料参数表

3)固体有限元模型建立。将液压衬套固体网格导入ADINA－Structure中，然后对衬套的各零件分别赋予材料属性。

液压衬套的主芯(包含金属骨架、限位块和橡胶主簧)与金属外套是通过金属骨架传力的，所以在金属骨架对应的节点施加6个自由度的全约束。

与台架试验加载方式相一致，有限元模型载荷施加在金属内套内表面的节点。在进行静、动特性仿真时，施加载荷的类型和方式是不同的，需要通过不同的时间步和时间函数来实现。

通过上述设置，建立了液压衬套固体有限元模型，如图3所示。

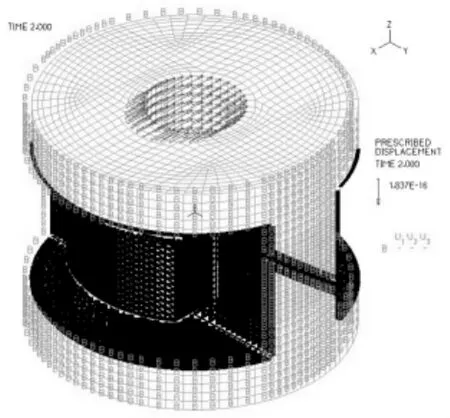
图3 液压衬套固体有限元模型

2.2 液压衬套液体有限元建模

1)液体网格的划分。对液压衬套的液体几何模型进行网格划分时，需保证固体结构和液体结构相接触的界面上的节点和单元一致。得到的液体网格如图4所示。该网格模型有9 260个单元，其中68个6节点的FCBI单元，9192个8节点的FCBI单元。

图4 液压衬套液体有限元网格模型

2)液体材料属性的确定。液压衬套中的油液为乙二醇水溶液，经试验测得其体积百分数为90%，密度为1.121×10－9t/mm3，20℃时的动力黏度为1.295×10－8MPa·s。

3)液体有限元模型的建立。将HyperMesh中的液体有限元网格导入到ADINA－F中进行材料和边界条件的设定。考虑到液压衬套主要是在低频下工作，惯性通道中的液体流速较低，按雷诺数的计算公式，可估算出衬套内液体的最大雷诺数小于临界雷诺数2 300，因此可将模型中的液体流动定义为层流(laminar)［9］。

液压衬套的液体边界主要有2种:由于金属外套刚度大且固定不动，同时考虑液体有一定的黏性，将液体与外套接触的界面定义为无滑移固壁;橡胶主簧刚度比金属材料小得多，液体与橡胶接触界面会在载荷作用下进行运动，因此将此界面定义为无滑移液固耦合面。在定义液固耦合面时，要注意和固体中的液固耦合面一一对应。

液压衬套液体有限元模型如图5所示。

3 液固耦合有限元仿真与试验验证

3.1 静态仿真与试验验证

静态仿真一般采用Statics方法，但为了研究液体对静特性的影响，本文采用准静态方法，即缓慢加载(加载时间尽量长)，使动态仿真逼近静态仿真。在动态缓慢加载过程中，液室和惯性通道中的液体流动比较缓慢，可以按层流处理。本文只研究液体起作用方向上的隔振性能，因此把该方向作为加载方向(X向)，其他两个方向不做研究。加载载荷从0 N均匀增长到1 000 N，时间历程为25 s。

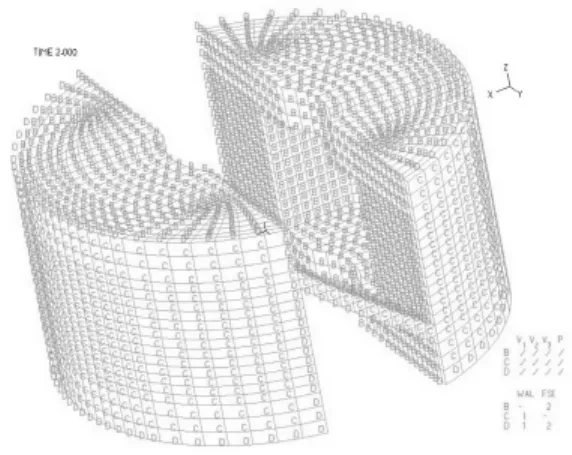
图5 液压衬套液体有限元模型

通过上述设置，将固体有限元模型和液体有限元模型分别导入液固耦合求解模块ADINA－FSI中进行耦合仿真，仿真结果在后处理模块ADINAProcessing中输出，如图6所示。从图6可知，橡胶主簧的变形主要发生在与内套接近的部位。

图6 橡胶主簧X向变形图(mm)

图7为加载过程中t=25 s时刻的液体压力分布图，可见在准静态加载过程中，由于是均匀缓慢加载，故衬套内液体压力分布比较均匀且压力值很小。

为了验证有限元仿真的正确性，对液压衬套进行台架试验。在静刚度测量中，试验机从0 N开始以40 N/s的速度对衬套X向进行匀速力加载，加载时间为25 s。

图7 液体压力分布图(MPa)

根据仿真和试验数据绘制力－位移曲线，如图8所示。可见，有限元模型对衬套静刚度的模拟是正确的。在大变形状态下衬套的静刚度出现非线性，而有限元模型由于对橡胶材料进行了简化而不能进行模拟。

图8 液压衬套仿真静刚度与试验值

3.2 动态仿真与试验验证

对衬套内套上的所有节点施加X向的位移谐波激励，激励幅值为0.375 mm，频率选取了1～40 Hz内几个典型值。利用几何作图法［10］计算这些频率下的动刚度和阻尼滞后角，得到该振幅下的动刚度曲线和阻尼滞后角曲线，如图9所示。

液压衬套动刚度和阻尼滞后角仿真曲线与试验曲线的趋势相吻合，但数值偏小，且随着频率增大偏差变大。数值偏小是由于有限元模型对实际结构进行了简化，同时忽略了橡胶主簧本身的阻尼造成的。将橡胶材料作为线弹性材料处理不能模拟出橡胶主簧动刚度随着频率增大而变大的趋势。

综上分析，建立的液压衬套液固耦合有限元模型是正确的，但在实际应用过程中需要进行适当的修正。

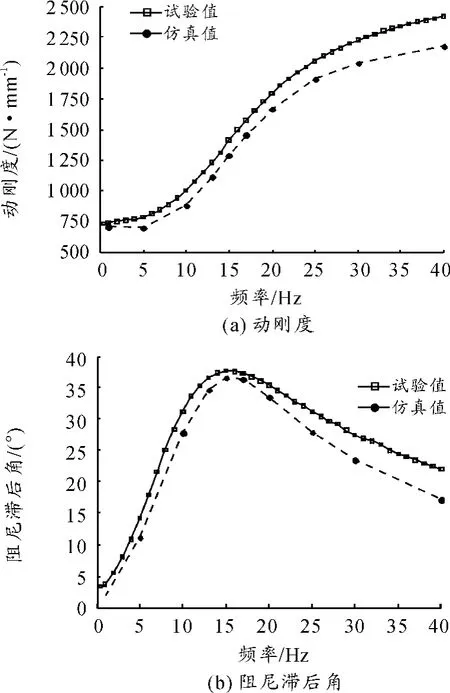
图9 动态特性试验和仿真曲线

4 有限元方法计算液压衬套体积刚度

体积刚度用来反映液室壁面膨胀能力。设液室内压力变化为ΔP时，由压力变化导致液体体积变化ΔV，则体积刚度定义如下:

获得体积刚度一般有2种方法:试验法［11］和有限元分析法［2］。试验法更精确，但方法复杂不易操作。有限元分析法容易实现且成本低。固定液压衬套的内、外套，增加液室中液体的体积，测量液室内的压力，获得体积与压力的变化关系，即可计算得到体积刚度。

由于液压衬套的两个液室是相同的，且惯性通道对液室的体积刚度没有影响，所以将惯性通道去掉并取一半模型进行有限元分析，如图10所示。其中液体模型中增加了一个小立方体网格单元，用于增加液室中液体的体积。

将上面的网格单元导入ADINA进行设置。固体模型中对金属内套和金属骨架外表面施加固定约束，液体模型中与金属外套接触的液体表面和小立方体4个侧表面均定义为固壁，小立方体顶面定义为移动壁面。对移动壁面施加X向位移载荷，将小立方体中的液体推入液室。仿真时间为10 s。图11为第6 s时刻的仿真结果。

图10 用于计算体积刚度的有限元模型

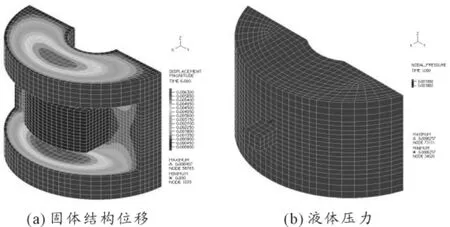
图11 模型仿真结果

固体模型结果反映出液室体积膨胀主要发生在上下两端橡胶壁面上，壁面厚度和橡胶材料参数直接影响体积刚度。液体模型反映出液体压力的变化。由于模型是缓慢加载，所以压力分布基本是均匀的，只需测得一点的压力值即可代表整体压力。

根据仿真过程中液室中油液体积和压力的变化，可以得到单液室体积刚度为 2.62×1011Pa/m3。

5 利用有限元模型验证参数化模型优化结果

液压衬套的AMESim参数化建模能够方便快捷地计算衬套各参数对其动特性的影响，进而通过改变不同参数实现衬套性能的优化［8］，但优化结果是否在结构上满足需要，需要通过有限元法验证。

本文所研究的液压衬套通过AMESim参数化建模与分析得到阻尼滞后角曲线，见图12(a)。图中常见振幅曲线对应的峰值频率区间为7～15 Hz。为了匹配整车悬架系统，需将频率区间移到11～17 Hz。利用参数化模型进行优化(优化结果见图12(b))，所得最优方案需对惯性通道的长度和截面积进行修改。

根据优化结果修改有限元模型，其仿真结果如图13所示，与AMESim仿真结果一致。

图12 优化前后液压衬套的阻尼滞后角

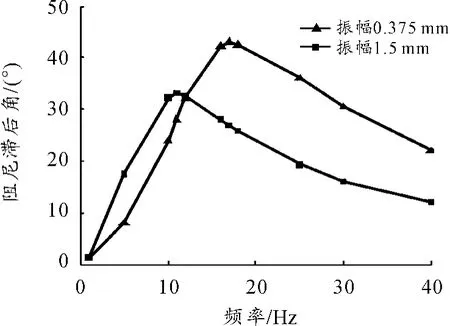
图13 有限元仿真结果

6 结论

利用ABAQUS和ADINA建立了液压衬套的液－固耦合有限元模型，仿真分析其静、动态特性并进行试验验证。在此基础上仿真计算其关键参数体积刚度，得到如下结论:

1)该有限元模型能够有效模拟液压衬套的静、动态特性，为进一步对衬套进行动力学性能改进提供基础。

2)利用有限元方法可以获得液压衬套液室体积刚度，为相关参数化分析工作提供指导和借鉴。

3)有限元方法可以对衬套参数化模型优化结果进行结构验证。

［1］ 上官文斌，徐驰.汽车悬架控制臂液压衬套动态特性实测与计算分析［J］.振动与冲击，2007，26(9):7－10.

［2］ 上官文斌.液阻型橡胶隔振器液－固藕合动力学特性仿真技术研究［D］.北京:清华大学，2003.

［3］ SHI Wen－ku，CHEN Zhi－yong.Finite Element Analysis of the Static and Dynamic Characteristics of Engine Rubber Mount［Z］.PACIIA，2009.

［4］ CHEN Zhi－yong，SHI Wen－ku.Finite Element Analysis of Light Vehicle Cab’s Hydraulic Mount Based on Fluid－Structure Interaction Method［J］.SAE，2011(1):604.

［5］ 潘孝勇.橡胶隔振器动态特性计算与建模方法的研究［D］.浙江:浙江工业大学，2009.

［6］ Gil－Negrete N.Predicting thedynamicbehaviourof hydrobushings［J］.Shock and Vibration，2002，12:91－107.

［7］ Karlsson F，Persson A.Modelling non－linear dynamics of rubber bushing－Parameter Identification and Validation［D］.Sweden:Master’s Dissertation，Lund University，2003.

［8］ 刘亚川.悬架液压衬套有限元分析与基于AMESim的隔振性能优化［D］.长春:吉林大学，2013.

［9］ 岳戈，梁宇白.ADINA流体与流固耦合功能的高级应用［M］.北京:人民交通出版社，2010.

［10］王光(译).硫化橡胶动态性能试验方法［J］.噪声与振动控制，1987，3:52－57.

［11］吕振华，上官文斌.液阻悬置动态特性实验方法及实测分析［J］.中国机械工程，2004，15(2):182－186.

(责任编辑 刘 舸)

Fluid-structure Interaction Finite Element Analysis of Hydrobushing Used in Suspension

QIN Min1，JIANG Yong－feng1，MA Tian－fei2，LIU Ya－chuan2，ZHANG Min－min2
(1.R＆D Center，China Faw Co.Ltd.，Changchun 130012，China; 2.State Key Laboratory of Automobile Simulation and Control，Jilin University，Changchun 130022，China)

As the important vibration isolator used in suspension system，analyses of static and dynamic characteristics and matching of vibration isolate performance for hydrobushing are important in research and development.Based on fluid－structure interaction finite element method，FSI finite element model of hydrobushing is built.The static and dynamic simulation of the FSI model are conducted to validate the model.Based on the verified model，key parameters of hydrobushing are simulated.The parameters will provide guidance for the test and parametric analysis.Meantime，the method is used to verify the results of parametric analysis.

hydrobushing;fluid－structure interaction;finite element analysis

U463

A

1674－8425(2014)07－0005－06

10.3969/j.issn.1674－8425(z).2014.07.002

2014－05－08

吉林省科技支撑计划资助项目(20106003)

秦民(1974—)，男，吉林长春人，博士研究生，高级工程师，主要从事车辆操稳平顺性研究。

秦民，蒋永峰，马天飞，等.悬架液压衬套液固耦合有限元分析［J］.重庆理工大学学报:自然科学版，2014 (7):5－10.

format:QIN Min，JIANG Yong－feng，MA Tian－fei，et al.Fluid－structure Interaction Finite Element Analysis of Hydrobushing Used in Suspension［J］.Journal of Chongqing University of Technology:Natural Science，2014(7):5－10.