离退休人员参加城镇职工基本养老保险人数的ARMA预测

孙学强

(河海大学理学院，南京 211100)

离退休人员参加城镇职工基本养老保险人数的ARMA预测

孙学强

(河海大学理学院，南京 211100)

介绍了基于时间序列建立ARMA模型的基本理论，并结合这些理论对我国离退休人员中从1989年到2011年的参加城镇职工基本养老保险的人数建立了ARMA(1，1)模型，并预测了从2012到2015年的参保人数。

时间序列;ARMA模型;养老保险;Eviews软件;预测

离退休人员参加养老保险的人数是反应人口老龄化的一个重要指标。因此，预测短期内离退休人员参加养老保险的人数对于国家的统筹规划具有重大意义。

韩烨［1］指出，离退休人员参保率以4.92%的增长率逐年上升。针对近几年统计数据［2］的研究及本文预测发现其实际增长率不止于此。目前，国内尚无离退休人员参加养老保险的预测研究，因此，本文将采用ARMA模型对离退休人员参加城镇职工基本养老保险的人数进行预测。这种建模方法不仅是数学知识在生活中的应用与推广，而且能预测出离退休人员参加养老保险的情况，为政府的预算及养老保险账户的登记与管理提供参考。

数据的模型预测方法有很多，但要求采用的方法能保证预测得出的数据相对精确，并能通过模型的理论检验。文献［3］介绍了时间序列几个基本模型的基本理论;文献［4］介绍了利用Eviews软件对时间序列数据进行建模操作与计算的方法。目前经常应用的方法主要有线性时间序列的AR模型、MA模型、ARMA模型3种模型，最后一种模型可以看做是前2种的综合，同时应用ARMA模型进行建模已成为处理时间序列数据的热点，并可达到很好的结果［5-6］。例如:范玉妹等［7］应用ARMA(2，2)模型对北京市人均GDP进行了短期预测，精度较高;王悦［8］采用ARMA(2，2)模型对上海经济增长GDP进行了预测分析，结果表明拟合效果较好;王义等［9］应用ARMA(3，3)模型对恒生指数进行预测，MAPE值为1.445%，精度较高。因此，本文将采用时间序列ARMA理论对我国离退休人员参加养老保险人数进行建模预测。

模型的识别与建立的主要步骤有模型的定阶与参数估计、模型的检验与模型的预测。本文主要利用Eviews软件进行上述操作。

1 模型的定阶与参数估计

1.1 模型的定阶

去除时间趋势和常数项的序列经过平稳性检验稳定后，通过观察自相关系数和偏相关系数的拖尾与截尾性质来确定ARMA(p，q)模型的阶数p 和q。3种模型的性质见表1。

表1 拖尾性和截尾性

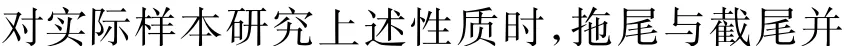
2 模型检验与预测

ARMA(p，q)模型的检验主要是参数检验和残差分析检验。参数的检验即看模型的各参数是否显著，一般参数显著性水平小于5%就能达到要求。残差分析检验主要检验残差序列是否为白噪声，若是，则模型误差项的S阶自相关系数为0，误差项即是一个白噪声过程，建立Q统计量。

Q统计量近似服从χ2S-p-(q)分布，则在显著性水平α下，当Q＞S-p-(q)时认为残差是白噪声序列，模型通过检验。

采用最小均方误差预测法，利用Eviews软件进行预测。预测分静态和动态预测。一般静态预测较为准确，但只能预测下一年的数据。本文采用动态预测，可以预测较长时间段的数据。

3 我国离退休人员参加养老保险的人数预测

本文数据是来自文献［2］的中国财政年鉴从1989年到2011年离退休人员参加养老保险的人数，具体见表2。

表2 我国从1989年到2011年离退休人员参加养老保险人数

我国从1989年到2011年离退休人员参加养老保险人数的趋势如图1所示。

图1 离退休人员参加养老保险人数

对其进行单位根检验后发现，去除时间趋势和常数项的二阶差分后序列平稳，检验结果如表3所示。

表3 单位根检验结果

图2 二阶差分的相关系数

根据AIC最小准则(表4)，采用ARMA(1，1)进行建模预测。计算得出模型参数估计结果如表5所示。

表4 各种模型的AIC值

表5 模型的参数估计结果

此时，所有参数在5%水平下具有显著性，且模型的特征方程的2个根都在单位圆外。再次考虑对ARMA(1，1)模型进行残差检验，见图3。

图3 模型残差项的自相关系数及Q值检验

表6 模型的预测值与实际值

模型的实际值与预测值在相对误差限为0.8%的范围内预测效果较为准确，预测结果见图4。

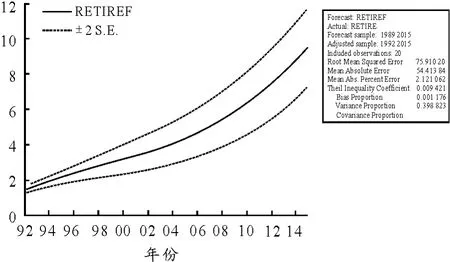
图4 模型ARMA(1，1)的预测结果

预测序列中平均绝对百分误差MAPE值为2.12，满足平均绝对百分误差值在0～5之间，模型合理。

4 结束语

应用ARMA(1，1)模型预测我国的离退休人员参加养老保险人数结果反映的短期预测效果较好，可以看出我国的离退休人员参加养老保险呈逐年递增的情况。但这只是利用统计数据进行建模预测的，我国尚存在着部分偏远地区达到年龄而未参加养老保险的人。从模型上看，长期预测会使误差逐渐变大，因此为了数据精确性，采用短期预测效果较为明显。

［1］韩烨.从制度赡养率看我国养老保险基金发展面临的挑战［J］.经济纵横，2013(2):86-90.

［2］何杰平.参加城镇企业职工基本养老保险人数［M］.北京:中国财政年鉴，2013.

［3］何书元.应用时间序列分析［M］.北京:北京大学出版社，2003.

［4］张晓峒，EVIEWS使用指南与案例［M］.北京:机械工程出版社，2007.

［5］梁妍，夏乐天.时间序列ARMA模型的应用［J］.重庆理工大学学报:自然科学版，2012(8):106-109.

［6］居浩，欧家福，邵毅敏.ARMA预测算法在汽车驱动桥齿轮故障诊断上的应用［J］.重庆理工大学学报:自然科学版，2012(2):17-24，39.

［7］范玉妹，玄婧.ARMA算法在GDP中的应用［J］.江南大学学报:自然科学版，2010(6):736-740.

［8］王悦.基于ARMA模型的上海经济增长预测与趋势分析［J］.区域经济，2012(7):108-113.

［9］王义，殷晓时.基于ARMA模型对恒生指数的实证分析［J］.山东理工大学学报，2012(3):31-33.

(责任编辑 何杰玲)

Predetermination of the Number of Retired People who Participate in the Urban Workers’Basic Endowment Insurance

SUN Xue-qiang
(College of Science，Hohai University，Nanjing 211100，China)

The article introduces the basic theories of building the ARMA model in time series.With the help of these theories，we build the ARMA(1，1)model in the retired people of our country who participate in the urban workers’basic endowment insurance from the year 1989 to 2011，and forecast the data from 2012 to 2015.

time series;ARMA model;endowment insurance;Eviews software;predetermination

O213

A

1674-8425(2014)08-0117-04

10.3969/j.issn.1674-8425(z).2014.08.024

2014-02-16

国家自然科学基金资助项目(50979029);河海大学自然基金资助项目(2008431111)

孙学强(1987—)，男，安徽阜阳人，硕士研究生，主要从事应用统计学研究。

孙学强.离退休人员参加城镇职工基本养老保险人数的ARMA预测［J］.重庆理工大学学报:自然科学版，2014(8):117-120.

format:SUN Xue-qiang.Predetermination of the Number of Retired People who Participate in the Urban Workers’Basic Endowment Insurance［J］.Journal of Chongqing University of Technology:Natural Science，2014(8): 117-120.