一类带可变库存费用和短缺量延期供给的库存模型
兰德新,赵萌
(武夷学院数学与计算机学院,福建武夷山 354300)
一类带可变库存费用和短缺量延期供给的库存模型
兰德新,赵萌
(武夷学院数学与计算机学院,福建武夷山 354300)
研究当库存费的变化率为存贮时间函数h(t)时,在允许缺货、缺货部分延期供给、拖后率为β(t)=e-kt,k>0,t是等待时间的情况下,易变质产品的最优策略。利用最小二乘法原理和泰勒展开分析了易变质产品最优策略的算法,并给出算例进行仿真。仿真结果证明了算法的有效性。
可变库存费;拖后率;需求依赖;库存模型
近几十年来,不少研究者致力于易变质的部分短缺延期供给问题的研究。文献[1-2]考虑变质、短缺量部分拖后等因素,建立了单一产品的订价和批量的库存模型;文献[3]研究了允许缺货且带数量折扣的腐烂物质库存模型;文献[4]考虑时变需求下易腐蚀性物品部分的拖后问题;文献[5]研究了需求率依赖于价格和时间的部分短缺量拖后问题。上述问题都未考虑可变库存费的问题,而在实际的库存系统中,单位产品的库存费或单位时间的库存费是可变的。例如,文献[6]中每单位物品的库存费分别为存贮时间和存贮量的非线性多项式函数;文献[7]将可变库存费用引入到需求受库存影响的模型中;文献[8]中需求率依赖于当前的库存量,变质性物品的变质率为常数,研究利用单位产品或单位时间库存费为大于0的可导函数来建立模型,但模型不允许缺货。目前,不少研究者致力于易变质的部分短缺延期供给问题和可变库存费的问题相结合的研究。例如,文献[9]在文献[8]研究的基础上考虑允许短缺且短缺量完全延期供给的情形;文献[10]研究了部分短缺量延期供给和可变库存费用的变质性物品的库存模型。
本文将在上述文献的基础上,同时考虑需求受库存影响且在拖后率β(t)=e-kt(k>0,t是等待时间)的情况下建立可变库存费用的易变质产品的库存模型。
1 数学模型
考虑一类易变质产品的库存问题,这类产品随着库存量的增加需要采取一些防护措施,从而导致了库存费用的变化。对于这种情形,可以假设库存费用HC满足微分方程dHC/dI=h(t)。其中,h(t)和h'(t)在(0,+∞)内均大于0。
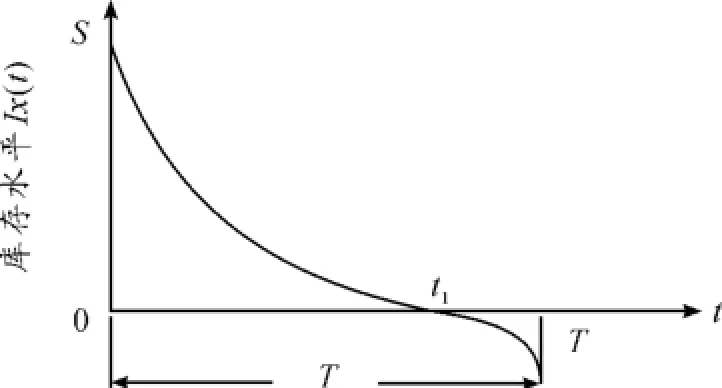
图1 产品的库存水平变化曲线
在(0,+∞)内,利用图1描述系统的库存水平的变化状态。假设系统从0时刻开始运作并且0时刻库存水平为S,此后产品以一定的速率连续出售,则t时刻需求率为α+βI(t)。其中:α>0代表产品的市场基础,β>0,I(t)表示t时刻的库存水平;易变质产品的变质率为θ。由于连续的需求和产品自身的变质使得库存水平不断下降,最终假定在t1时刻,库存水平下降到0。在t1时刻后,继续到来的需求量拖后补给,拖后率是β(t)= e-kt,k>0,t是等待时间。

显然,当0<t1<T时,库存系统在[t1,T]内发生缺货;当t1≥T时,库存系统在[0,T]内不会发生缺货。
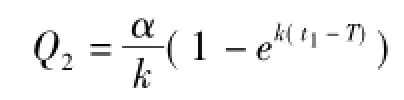
系统在[0,T]时间内的各项费用计算如下:
1)库存费用为


2 模型分析


3 算法与算例仿真

4 结束语
本文针对库存费用HC满足微分方程dHC/dI =h(t),且短缺量部分拖后的情形,建立了单一易变质产品的库存模型,同时考虑了易变质产品的变质损失、缺货损失和丢单损失。采用最小二乘法原理及泰勒展开对模型进行分析和近似求解,给出求解最优策略的算法步骤,并对算例进行仿真,得到近似最优策略(T*,t*1)。在今后的研究中,可在以下方面对变质性产品的库存问题做进一步推广研究,例如考虑需求率为随机波动量的情况和库存费用为库存量的函数等情况。
[1]Abad P L.Optimal pricing and order size for a reseller under partial backordering[J].Computers and Operations Research,2001,28:53-65.
[2]Papachristos S,Skouri K.An inventory model with deteriorating items,Quantity discount,pricing and time-dependent partial backlogging[J].International Journal of Production Economics,2003,83:247-256.
[3]莫降涛,徐春明.允许缺货且带数量折扣的腐烂物质库存模型[J].数学的实践与认识,2010(5):1-8.
[4]Chang H J,Dye C Y.An EOQ model for deteriorating items with time varying Demand and partial backlogging[J].Jopl Res Soc,1999,50:1176-1182.
[5]Abad P L.Optimal pricing and lot sizing under conditions of perishability and partial backordering[J].Management Science,1996,42:1093-1104.
[6]Goh M.EOQ models with gengral demand and holding cost functions[J].Eu-Ropean Journal of Operational Research,1994,73:50-54.
[7]Muhlemann A P,Valtis Spanopoulous N P.A variableholding cost rate EOQ Model[J].European Journal of Operational Research,1980,4:132-135.
[8]毛晓丽.变库存费的变质性物品的最优订货策略[J].经济数学,2001,18(3):70-74.
[9]闵杰.带有可变库存费用和短缺的变质性物品的经济批量模型[J].数学的实践与认识,2008,38(11):1-6.
[10]何鲲,鹿泉育.考虑变库存费用和销售机会损失的库存模型[J].合肥工业大学学报,2010,33(11):1717-1720.
(责任编辑 杨黎丽)
An Inventory Model with Variable Holding Cost
and Shortage Postponed Delivery
LAN De-xin,ZHAO Meng
(Mathematics and Computer Department,Wuyi University,Wuyishan 354300,China)
In this paper,when out of stock is allowed,and stock parts supply is deferred,the delayed rate is β(t)=e-kt,k>0,t is the waiting time.It studies the optimal replenishment and pricing strategy of a single perishable product.Using the least square method and the Taylor expansion,this paper analyzes the optimal order of perishable products and pricing strategies of the algorithm,gives examples and describes the simulation algorithm.
variable holding cost;partial backlogging rate;stock-dependent demand;inventory model
O227
A
1674-8425(2014)03-0127-04
10.3969/j.issn.1674-8425(z).2014.03.023
2013-12-18
福建教育厅科技基金资助项目(JA10269)
兰德新(1964—),男,副教授,主要从事随机优化及其应用研究。
兰德新,赵萌.一类带可变库存费用和短缺量延期供给的库存模型[J].重庆理工大学学报:自然科学版,2014(3):127-130.
format:LAN De-xin,ZHAO Meng.An Inventory Model with Variable Holding Cost and Shortage Postponed Delivery[J].Journal of Chongqing University of Technology:Natural Science,2014(3):127-130.

