基于改进型TSP观测装置的地震波场数值模拟

周竹生, 齐红伟

(中南大学 地球科学与信息物理学院， 长沙 410083)

0 引言

隧道施工过程中往往面临如断层、破碎带、溶洞等不良地质体，一旦发生事故，将给施工单位、人民乃至国家带来严重损失。因此高效准确预测施工前方地质情况至关重要。目前很多专家学者对隧道超前探测方法进行了研究，但大部分是基于探测方法在工程实际中的成功应用，对其存在的技术缺失和失败情况以及理论研究较少。

现有的定向探测数据采集方法有两类：①瑞士安博格公司生产的TSP系列仪器和国产TGP等超前探测系统；②美国TRT和国产TST等超前探测系统[1-3]。由于隧道超前预报的特点决定了施工场地大多为狭小的隧道空间，且必须具有高效性、实时性、高精度等技术特性，而且实际探测得到的地震波场同时存在纵波、横波、转换波等，使得波场信息非常复杂，因此对超前探测地震波场的传播规律和机理进行分析是很有必要的。地震波场数值模拟[4,5]则是最为直接有效的方法。近年来很多学者对隧道地震波场进行了研究。有的利用声波方程，但无法模拟隧道复杂地质情况下的波场传播机理；有的利用有限元[6]或者伪谱法[7]进行数值求解，而有限元法计算量大，对计算机内存要求高，降低了计算速度；伪谱法虽然计算效率高，但是其基于全域计算的特点决定了空间一点数值发生变化即可导致频率域所有值发生变化。有限差分法则是用差分代替微分，因其具有网格剖分灵活等特点而在地震波场数值模拟中得到了广泛应用。随着交错网格和高阶有限差分方法的提出，理论上更是可以得到任意高阶精度的时空差分格式，模拟的波场在精度上有了很大的提高。因此通过对比现有TSP观测装置的优缺点，从提高施工效率、可行性和准确性角度出发，对现有TSP观测装置进行了有效改进[8]；同时推导了基于一阶速度—应力弹性波动方程的高阶交错网格有限差分格式，并在此基础上模拟了基于改进TSP观测装置下的地震波场，从而为后续研究提供了可靠的理论数据。

1 TSP观测装置的改进

1.1 现有TSP观测装置的优缺点

隧道地震超前预报(TSP)，是根据地震反射波法勘探原理对隧道掌子面前方地质情况进行预报的，如瑞士安博格公司生产的TSP系列，其工作方法是在距离掌子面一定范围内的隧道壁上等间距地布设起爆点，采用微弱爆炸震源进行爆破，产生的地震信号在隧道周围岩体内传播，遇到弹性界面时地震波发生反射，反射波携带前方弹性界面的信息，被三分量传感器接收，经过数据处理便可得知前方地质体情况。观测系统如图1所示。

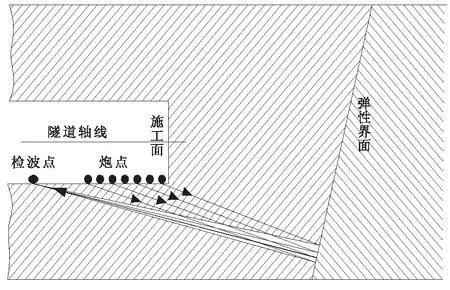
图1 现有TSP观测系统示意图Fig．1 Schematic diagram of the existing TSP observation system

该方法的优点是：适用范围广，探测距离长，对隧道施工影响小，提交资料及时等。

该方法的缺点是：采用炸药震源，不能重复叠加，使得资料信噪比低；施工过程需要一定的隧道空间，而且只能对掌子面前方进行探测，对隧道顶底界面信息掌握不足等。

1.2 TSP观测装置的改进

针对现有方法存在的不足，本研究采用的改进型TSP观测装置是在掌子面上朝向定向探测方向布设钻孔，钻孔内安设传感器串，在钻孔周围采用锤击震源，利用多路地震信号采集仪器进行接收[8]，其观测系统如图2所示。

该方法使用锤击震源，可进行多次重复叠加；不同方向激发的地震波，对前方的构造反射特征不同，携带了不同的信息，有利于更精细的地质解释，而且该方法可以在狭小的隧道空间进行施工探测，钻孔方向改变灵活，极大地提高了施工效率，获得多方位的反射波，同时将隧道对波场的影响降到最低，突出有效波，给理论研究和资料处理带来很大的方便。

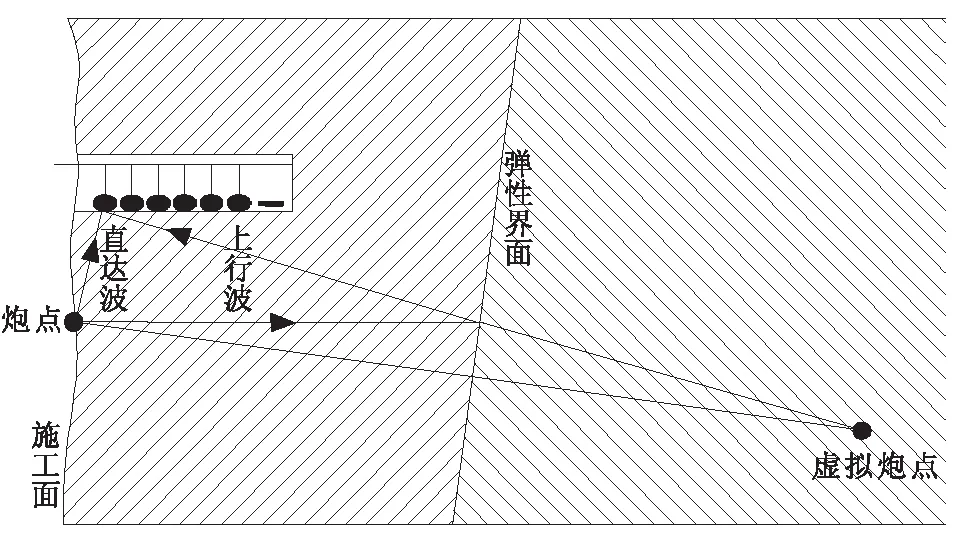
图2 改进型TSP观测系统示意图Fig．2 Schematic diagram of the improved TSP observation system

2 正演模拟方法

2.1 交错网格高阶有限差分

弹性各向同性介质中一阶速度—应力弹性波动方程为：

(1)

其中vx、vz分别为质点振动位移的水平分量和垂直分量；σxx、σzz分别为质点在水平方向和垂直方向的正应力；σxz为质点在xz平面内的切应力；λ、μ为拉梅常数。

对式(1)进行差分离散，得到的时间二阶、空间八阶有限差分方程如式(2)所示。

(2)

其中U、V分别为vx、vz的离散量；R、T、H分别为σxx、σzz、σxz的离散量；i、j、k分别为x、z、t的离散序号。

2.2 边界条件

在隧道超前探测全波场正演模拟过程中将遇到三种边界条件：①自由边界条件；②人工边界条件；③弹性边界条件。

1)自由边界是地质介质与空气介质接触的边界，如地面、隧道壁等。由于本研究设计的是深部隧道模型，因此可以忽略地面处自由边界，而只处理隧道壁自由边界，但是该观测装置在较小的隧道空间即可施工作业，且传感器串是安放在掌子面前方的钻孔内，所以隧道影响特别小，甚至可以忽略不计。因此本研究忽略隧道侧壁的影响，将掌子面看做自由边界，采用应力镜像法进行处理[9]。

2)人工边界是用有限模型模拟地下无限空间时进行人为截断造成的反射边界，波传到人工边界时会产生严重反射，甚至影响有效波的识别，因此必须要进行适当的处理。作者采用最佳匹配层(PML)边界条件[10]进行处理。

3)弹性边界是弹性参数不同的两种介质的分界面，因此在数值模拟过程中可以通过设置弹性参数实现。

2.3 震源函数

震源处理是弹性波数值模拟中的一个重要环节，是算法精确与否的前提条件。数值模拟过程中常用的是点源，即将震源看成一个点上的激励。

本研究采用的是主频400 Hz负极性的Ricker子波，波形如图3所示。

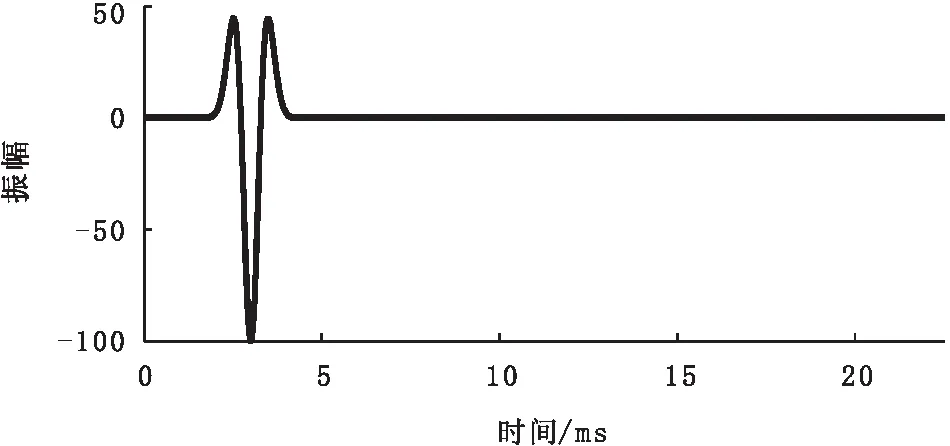
图3 Ricker子波Fig．3 Ricker wavelet

3 模型正演

本次研究设计两个简易模型，模型一(图4(a))为倾斜的软弱夹层模型；模型二(图4(b))为均匀半空间中带有一个20 m×20 m的方形空洞，物性参数如表1所示。模型大小为200 m(深)×200 m(宽)，网格间距0.25 m，时间采样间隔为10-5s，道间距0.25 m，40道同时接收，零偏移距。

图4 速度模型Fig．4 Velocity models(a)夹层模型；(b)方形空洞

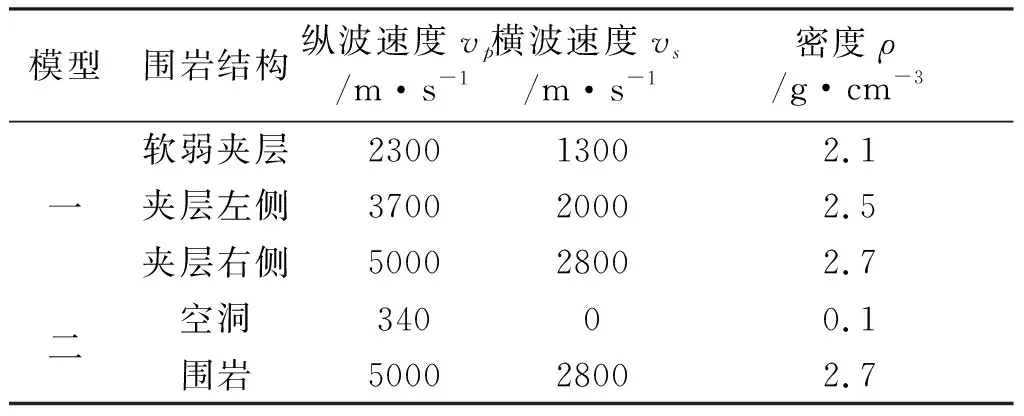
模型围岩结构纵波速度vp/m·s-1横波速度vs/m·s-1密度ρ/g·cm-3一软弱夹层230013002.1夹层左侧370020002.5夹层右侧500028002.7二空洞34000.1围岩500028002.7

图5是模型一30 ms时刻的波场快照；图6是水平分量对应的单炮记录，记录时间长度为60 ms，S1、RP11、P2、RS1、S2、RP21、P-S分别代表直达横波、夹层左侧一次反射纵波、二次下行纵波、一次反射横波、二次下行横波、夹层右侧一次反射纵波以及转换波。从图5中可以看出软弱夹层的透射波和界面反射波，并能判断出夹层的倾斜方向。在图6中，直达横波、反射波以及多次反射波清晰可见。根据时深关系，纵波到达末道的初至时间是0.002 7 s，但由于本文参数设置关系，以及掌子面自由边界产生的面波的影响，使得直达纵波能量很弱，直达横波能量较强。由于软弱夹层内介质波阻抗小于围岩介质，所以前界面反射系数为负数，使得入射波极性反转；根据单炮记录中记录到的夹层前后反射波的旅行时，在已知介质速度的情况下，可以通过计算得到夹层的厚度。如图6所示，RP11和RP21分别为夹层前后界面一次反射波，以第40道检波器为参考，RP11到达检波器的时间是29.08 ms，RP21到达检波器的时间是49.28 ms，夹层内纵波速度是2 300 m/s，在假设纵波垂直入射并且无衰减的情况下，估算夹层厚度约为23.23 m，与模型设计的24.75 m非常接近。

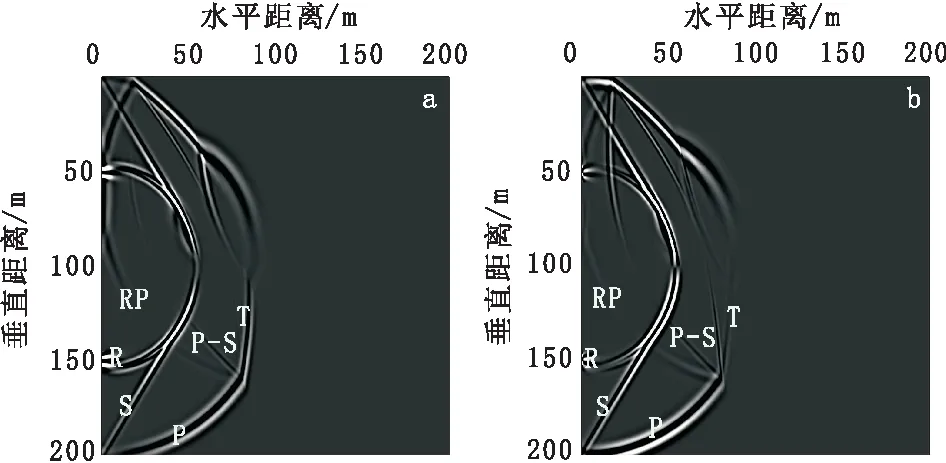
图5 模型一30 ms时刻波场快照图Fig．5 Model 1 snapshots of 30 ms

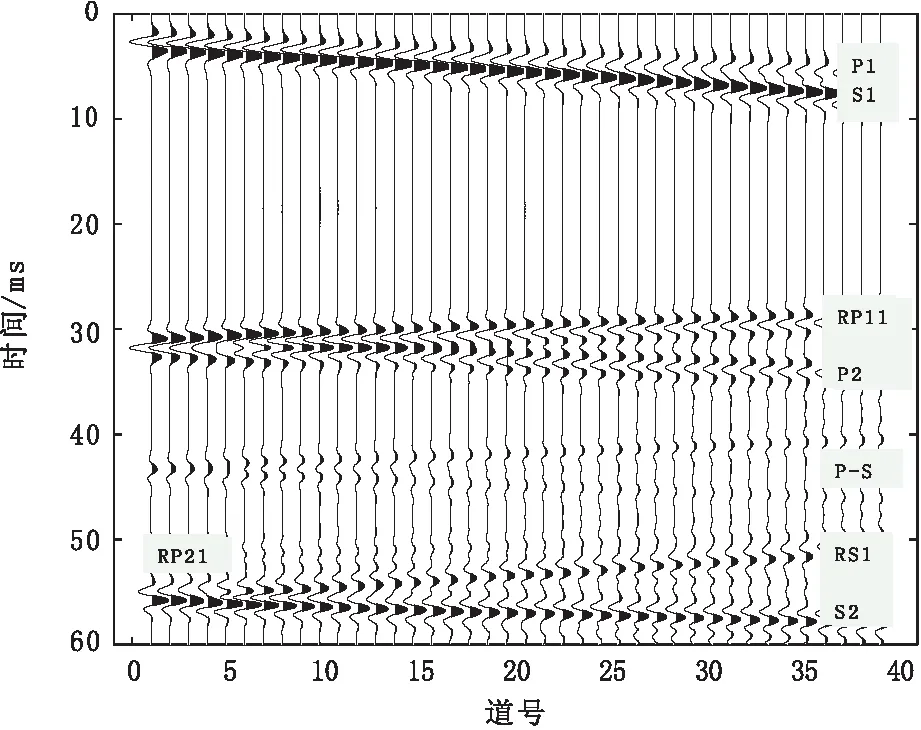
图6 模型一水平分量单炮记录Fig．6 Model 1 single shot record of horizontal comp

图7 模型二25 ms时刻波场快照图Fig．7 Model 2 snapshots of 25ms(a)水平分量；(b)垂直分量

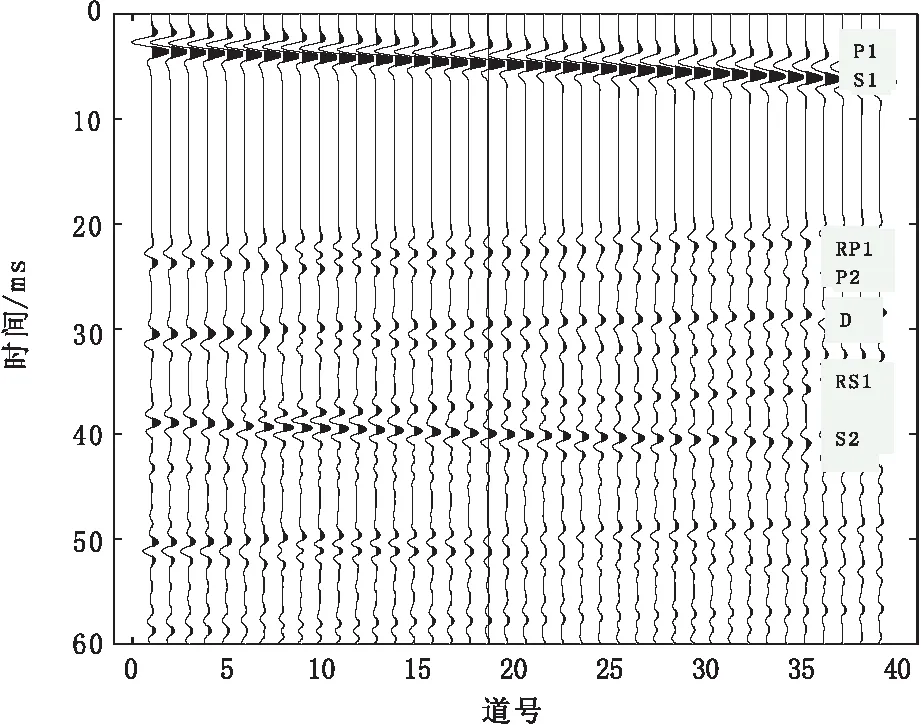
图8 模型二水平分量单炮记录Fig．8 Model 2 single shot record of horizontal component

图7是模型二25 ms时刻的波场快照图；图8是水平分量对应的单炮记录，记录时间长度为60 ms，图中S1、RP1、P2、RS1、S2、D分别代表直达横波、一次反射纵波、二次下行纵波、一次反射横波、二次下行横波以及绕射波。从图7中可以看出，由于洞内填充空气介质，横波无法传播，而纵波则穿过空洞继续传播。空洞角点处形成明显的绕射波(D)，从波场快照中基本能确定空洞的具体位置。在图8中，直达横波、一次反射波和多次反射波同相轴清晰可见，但由于绕射波、多次反射波的干涉叠加，使得波场较为复杂，同相轴发生弯曲。

4 结论

1)改进后的TSP观测装置易于实现，使用锤击震源可以重复叠加，提高资料信噪比；改进后装置可在狭小隧道空间内工作，钻孔方向改变灵活，可以探测隧道周围全方位的信息，提高预报精度；检波器串与钻孔良好耦合，降低隧道对波场的影响，易于数据处理和解释。

2)基于一阶速度—应力弹性波动方程的高阶交错网格有限差分法，能够有效地模拟改进后的TSP地震波场，模拟结果能够反映出隧道超前探测波场的传播机理，并能较准确地反应探测前方的软弱夹层、空洞等不良地质体的方位和规模，但在如何更加真实地模拟复杂地质情况下的波场特征还有待进一步研究。

3)本次研究尚处于理论研究阶段，意在为后续数据处理和解释以及工程实际应用提供理论基础。

参考文献：

[1] 刘志刚,刘秀峰.TSP(隧道地震勘探)在隧道隧洞超前预报中的应用与发展[J].岩石力学与工程学报,2003，22(8):1399-1402.

[2] 胡文武,陈一平,张玉贵. TSP203超前地质预报系统与应用实例[J]. 物探化探计算技术,2008,30(3):226-230，170.

[3] 戴前伟,何刚,冯德山.TSP203在隧道超前预报中的应用[J].地球物理学进展,2005,20(2):462-464.

[4] 冯英杰,杨长春,吴萍.地震波有限差分模拟综述[J]. 地球物理学进展，2007(22): 487-491.

[5] 武威,岳建华,邓帅奇,等. 煤巷地震超前探测合成记录的数值模拟方法研究[J]. 物探化探计算技术,2009,31(1):15-19，4.

[6] 王朝令.隧道地震超前预报中波场分离与反演方法的数值模拟研究[D]．西安：西安交通大学，2012.

[7] 李嫣.隧道超前探测地震波伪谱法数值模拟[J].福建建设科技，2011(4).

[8] 朱德兵.一种井巷定向探测地震勘探数据采集方法[P].中国,2012.

[9] Levander A R. Fourth-ordet finite-difference P-SV seismograms[J]. Geophysics,1988,53(11): 1425-1436.

[10] Collino,E,Tsogka C. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media [J]. Geophysics, 2001, 66(1): 294-307.