再议2011年山东高考理综卷第22题的定量解答

谢 佳 刘洪庆

(仁怀市酒都高级中学 贵州 仁怀 564500)

贵刊于2013年第6期刊发了“2011年高考山东理综卷第22题的定量求解”一文，笔者有幸研读后，感觉原文作者并未实现真正意义上对选项D的定量求解分析，于是产生了再议该题定量解答的想法．

1 原题和原作者解答简述

1.1 原题

题目：(2011年高考山东卷第22题)如图1所示，两固定的竖直光滑金属导轨足够长且电阻不计．两质量、长度均相同的导体棒c和d，置于边界水平的匀强磁场上方同一高度h处．磁场宽为3h，方向与导轨平面垂直．先由静止释放c，c刚进入磁场即匀速运动，此时再由静止释放d，两导体棒与导轨始终保持良好接触．用ac表示c的加速度，Ekd表示d的动能，xc和xd分别表示c和d相对释放点的位移．图2中正确的是

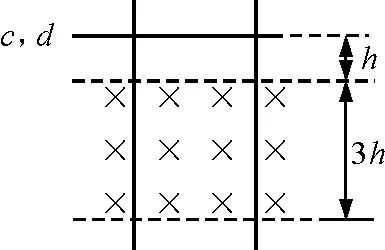
图1

图2

1.2 原作者解答简述

令d棒下落高度分别为h和2h时速度分别为v1和v2，则有

当c棒刚进入磁场时，合力为零，则有

由上述分析可得

(1)

又

则

(2)

由于v2>v1，故c棒离开磁场后(c棒出磁场时，d棒下落至2h处)，d棒所受安培力大于重力，d棒减速．令d棒离开磁场前任意时刻的速度为vt，加速度为a，则有

所以

(3)

由式(1)、(2)、(3)可得

(4)

由于d棒在磁场中受安培力作用后，加速度减小，根据平均速度和匀变速运动知识有

(5)

(6)

整理式(6)可得

解不等式得

其中一解不合题意舍去，即可得

2 定量解答再分析

从原作者的解答看，通过对速度的分析则判定出d棒的动能Ek和下落高度h之间的函数图像必然正确的观点值得商榷．笔者认为，这样的分析并不能给出佐证选项D正确的充分理由，更不能说明d棒从2h下落至4h过程中动能Ek与下落高度h之间的函数图像为什么是选项D中所呈现的图像.鉴于此，现对选项D做如下的定量回归分析．

2.1 寻找速度v与时间t的定量关系

令竖直向下为正向，d棒从2h下落至4h过程中任意时刻的加速度和速度分别为a和v，c和d的总电阻为R，则有

(7)

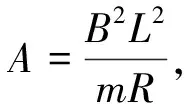
因此有

积分可得

ln(g-Av)=-At+C

(8)

当t=0，v=v0则

C=ln(g-Av0)

所以有

整理上式可得速度v与时间t的定量关系

(9)

2.2 寻找位移x与时间t的定量关系

令d棒下落过程中开始受安培作用的初位置为位移起点．根据式(3)可得

(10)

由式(10)有

积分可得

(11)

当t=0，x0=0，则

因此可得位移x和时间t之间的定量关系

(12)

2.3 原文作者定量分析回归

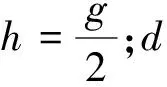
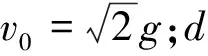
(13)

整理式(13)可得超越方程

(14)

解超越方程得

t=0.776 46 s

将t=0.776 46 s代入式(9)可得，d棒离开磁场时的速度v=1.19g．而c棒刚进入磁场时的速度

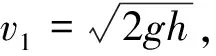
2.4 动能Ek与位移x函数关系的定量分析

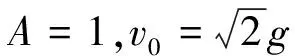
(15)

(16)

表1 动能Ek对应数据

由表1中动能Ek与位移x的对应数据，利用Excel工具处理数据可得图3．

图3

从图3可看出动能Ek与位移x的对应关系与D选项给出的d棒从2h运动至4h过程中函数关系图像吻合．结合图像，猜想d棒从2h运动至4h过程中动能Ek与位移x满足

Ek=Ek0e-bx

(17)

根据表1中动能Ek与位移x的对应数据，结合式(17)可得表2．

表2 动能Ek与位移x对应数据

在数据处理误差允许的范围内，可近似认为系数b为一定值，即b=0.037，猜想成立，则可得动能Ek与位移x之间的定量关系

Ek=Ek0e-0.037x

(18)

通过对上述定量关系的分析，充分佐证了选项D给出的函数图像的正确性，实现了真正意义上数理定量分析的良好愿望．本文是笔者的个人见解，希望读者再次求证．