逐差法处理打点纸带数据的研究
何述平
(西北师范大学教育学院物理教育研究所 甘肃 兰州 730070)
1 引言
打点纸带的数据处理是普通高中物理实验应用打点计时器(电磁、火花)研究匀变速直线运动的基本内容,数据处理方法之一的逐差法,前人虽有所论述[1~3],但较零星、笼统,且推理欠严谨,因此有必要对其进行较深入、系统的探究.
本文就此进行相应的研究,以期拓展处理打点纸带数据测定加速度、初速度的逐差法,解释存在的疑惑,进而为合理运用逐差法处理打点纸带数据奠定层次性、开放性的理论基础.
2 逐差法的推证
纸带随物体做匀变速直线运动,打点纸带的计数点为n,计数周期为T,连续计数点间的位移依次为s1,s2,…,sn,sn+1,…,如图1.
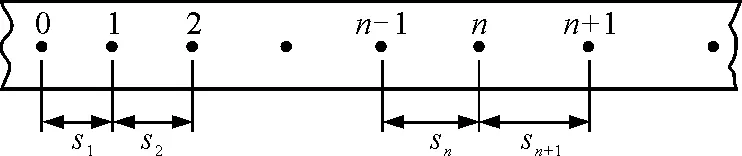
图1 打点纸带的计数点n和位移sn
计数点n-1与n间的位移为
(1)
式中n=1,2,3,…,v0为n=0时的瞬时速度.
计数点n的瞬时速度为
(2)
2.1 基本逐差法
2.1.1 位移逐差法(s-n逐差法)
由式(1)得
sn=s0+naT2
(3)
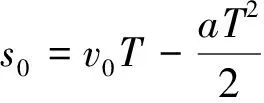
sn+k-sn=kaT2
(4)
式(4)求和,得
(5)
若取k=3,l=3;则有[3]

(6)
由式(5)或(6)就可确定加速度as.s0代入式(3)、再求和,得
(7)
若取N=6,式(6)代入,则有
(8)
由式(7)或(8)可确定初速度v0.
2.1.2 速度逐差法(v-n逐差法)
纸带做匀变速直线运动,则有
vn=v0+naT
(9)
式中n=1,2,3,….vn为间接测量量,应表示成直接测量量sn,T的函数;式(2)代入得
sn+sn+1=2v0T+2naT2
(10)
式(10)表明:sn+sn+1与n呈线性关系(v0,T,a为恒量);隔k项逐差、再求和,得
(11)
若取k=3,l=2;则有
(12)
由式(11)或(12)就可确定加速度av.式(10)求和,得
(13)
若取N=4,即n=1,2,4,5,式(12)代入,得
(14)
由式(13)或(14)可确定初速度v0.
2.1.3 速度-位移逐差法(v2-s逐差法)
纸带做匀变速直线运动,则有
(15)
式中n=1,2,3,….式(2)代入,得
8aT2(s1+s2+…+sn)
(16)
式(16)表明:(sn+sn+1)2与s1+s2+…+sn呈线性关系(v0,T,a为恒量);隔k项逐差、再求和,得
(17)
若取k=3,l=2;则有
(18)
由式(17)或(18)就可确定加速度av-s.式(16)求和,得
(19)
若取N=4即n=1,2,4,5,式(18)代入,得
(20)
由式(19)或(20)可确定初速度v0.
2.2 奇异逐差法
从不同角度考虑同一问题,或许是有益的;这便形成了处理打点纸带数据的奇异逐差法.
2.2.1 中时速度逐差法(v′-n逐差法)
纸带做匀变速直线运动,则有
(21)

(22)
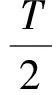
(23)
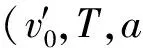
(24)
若取k=3,l=3;则有
(25)
式(24)或(25)可确定加速度av′,与位移逐差法的式(5)或(6)一致,可谓殊途同归.
由匀变速直线运动的速度规律,有
(26)
式(26)代入式(23)、再求和,得
(27)
若取N=6,式(25)代入,则有
(28)
式(27)或(28)可确定初速度v0,与位移逐差法的式(7)或(8)一致,可谓异曲同工.
参照图1,纸带做匀变速直线运动,则有
(29)
式中n=1,2,3,…,v0为n=0时的瞬时速度.
式(29)线性化[5],得
(30)
(31)
若取k=3,l=3;则有
(32)
(33)
若取N=6,式(32)代入,则有
(34)
由式(33)或(34)可确定初速度v0.
由上述5种逐差法的推证可见,逐差法形式简明,易于计算(代数形式、代数运算),其实质是差分-平均[5].
3 逐差法的运用及结果
取测北京地区重力加速度的打点纸带数据(g北京=980.12 cm/s2,T=0.04 s)[3],如表1;则依次运用上述推证的逐差法处理打点纸带数据测定加速度、初速度的结果如下.

表1 测定北京地区重力加速度的纸带数据
(1)位移逐差法的结果
由式(6)、表1得gs=977.08cm/s2;再由式(8)、表1得v0=36.88cm/s.
(2)速度逐差法的结果
由式(12)、表1得gv=976.56cm/s2;再由式(14)、表1得v0=36.97cm/s.
(3)速度-位移逐差法的结果
由式(18)、表1得gv-s=979.08cm/s2;由式(20)、表1得v0=36.20cm/s.
(4)中时速度逐差法的结果
由式(25)、表1得gv′=977.08cm/s2;再由式(28)、表1得v0=36.88cm/s.
(5)线性化逐差法的结果
上述5种逐差法处理打点纸带数据的结果表明,这5种逐差法的结果基本一致(重力加速度的相对误差依次为0.31%,0.36%,0.11%,0.31%,
0.77%);因摩擦、空气阻力,则实验测定值g实测应比公认标准值g北京偏小.因此,5种逐差法的结果具有合理性,进而说明5种逐差法具有合理性、可行性(以上各逐差法的结果与相应运用最小二乘法的结果[6]非常接近).
4 逐差法的讨论
4.1 逐差间隔
对式(5),由误差的方和根合成,并虑及s1,s2,…,sN相互独立,标准差均为σs;可得
(35)
式中k+l≤N,于是
(36)
式(36)表明:l=k时,σas最小;此时,测量数据s1,s2,…,sN配成对,即2k=N,这样可充分利用测量数据.因此,运用逐差法时,应合理选取逐差间隔[5][如式(6)、(25),式(12)、(18)、(32)同理].
4.2 逐差法的合理推证

鉴于:“先平均”法和“后平均”法各适用于两类本质不同的问题;虽然“先平均”法与“后平均”法的数学运算结果对相当多的具体问题相差甚微,但也不宜混用[7].因此,中学物理实验数据处理中,不仅不应运用“后平均”法,而且更没有必要涉及.
4.3 逐差法的特点及比较
逐差法的适用条件是因变量与自变量的函数形式为多项式和自变量等间距变化[5];因此,由式(3)、(10)、(16)、(23)、(30)知:位移逐差法、速度逐差法、中时速度逐差法、线性化逐差法是严格意义的逐差法,速度-位移逐差法是非严格意义的逐差法,即差值法[5];且它们均是一次逐差法[虽然由式(16)、(3)可推证二次速度-位移逐差法是严格意义的逐差法,并可推得相应的加速度计算式;但已显复杂,且因位移和的平方使误差放大以致加速度的计算结果欠合理].线性化逐差法因线性化导致不等权,应按不等权测量处理[5,9];然而,作为简化处理即仍按等权测量处理,可能使线性化逐差法的结果略偏离(加速度的结果略偏小,初速度的结果略偏大).逐差法作为解决拟合(回归)直线时方程数多于变量数的粗略方法(相对准确的最小二乘法而言)[5],可用于不要求计算标准差或不确定度的中学物理实验;因此,逐差法不失为简便、实用的中学物理实验数据处理方法.
比较位移逐差法的式(5)或(6)、速度逐差法的式(11)或(12)、速度-位移逐差法的式(17)或(18)、中时速度逐差法的式(24)或(25)、线性化逐差法的式(31)或(32)可知,逐差法处理打点纸带数据测定加速度的简捷程度(由简到繁)依次是:位移逐差法、中时速度逐差法、速度逐差法、线性化逐差法、速度-位移逐差法(同理,逐差法处理打点纸带数据测定初速度的简捷程度相同).因此,更宜采用位移逐差法处理打点纸带数据测定加速度、初速度.这就为逐差法处理打点纸带数据的层次性、开放性实验教学设计奠定了坚实的理论基础.
4.4 线性化逐差法的实质
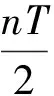
式(10)写成与式(30)对称的形式,有
(37)

4.5 逐差法的合理运用
就图2所示测量的位移x1,x2,…,xn,xn+1,…如何运用逐差法?有认为不可运用位移逐差法的式(6),否则就不合理,因为式(6)的前提条件是sn即连续相邻计数点间的位移(见图1);而且合理的数据处理方法应是速度-时间图像法[8].

图2 打点纸带的计数点n和位移xn
由式(6)知,合理运用位移逐差法测定加速度应是:取偶数个计数点,测量前、后半段位移即可;而不必依次测量xn.
若要测量xn,又要充分利用测量数据;那么怎样合理运用位移逐差法呢?纸带做匀变速直线运动,则计数点0和n间的位移为
(38)
式中n=1,2,3,…,v0为n=0时的瞬时速度.式(38)隔k项逐差,得
(39)
(40)
式(40)减式(39)即再隔l项逐差,求和得
(41)
若取k=4,l=2,m=2;则有
(42)
由式(41)或(42)(位移逐差法的另一形式)就可确定加速度ax.
而由式(5)取k=4,l=4,得
(43)
比较式(42)、(43)知:仅测量sn的前、后半段,由式(43)计算as较简捷;且式(43)更好地反映了数据测量方法与数据处理方法的辩证关系.
由式(5)、(41)的推证过程知:as和ax分别是一、二次位移逐差法的结果,且式(5)、(41)的适用条件不同(分别针对sn和xn);因此,式(5)、(41)不应混用,且由式(5)确定加速度as更简捷.
5 结束语
本文拓展化、具体化了处理打点纸带数据测定加速度、初速度的逐差法,提供了运用细致推证的5种逐差法的一个典型实例,比较了各逐差法的特点、简捷程度,探讨了合理运用逐差法的现实问题.逐差法可作为中学物理实验数据处理的实用方法,故本文的研究既可作为关于数据处理方法的高中物理课程资源,又可作为物理学方法论教育的显性方法的内容,是高中物理教师深入认识、教学设计打点计时器实验的理论基础;同时体现了高中物理课程内容理念的基础性、选择性,高中物理课程实施理念的多样性,并突出了开放性.可以预见,通过本文推证的处理打点纸带数据测定加速度、初速度的逐差法的探究式教学,可很好地培养物理实验的数据处理方法,可更好地理解匀变速直线运动的规律,进而提升物理实验的数据处理能力.
参考文献
1 许国梁,束炳如.中学物理教学法(第2版).北京:高等教育出版社,1993.357~358
2 陶洪.物理实验论.南宁:广西教育出版社,1996.184~188
3 王兴乃,罗栋国.高中物理实验大全(第1册).北京:电子工业出版社,1989.164~166,186
4 安忠,刘炳昇.中学物理实验教学研究.北京:高等教育出版社,1986.185~187
5 龚镇雄.普通物理实验中的数据处理.西安:西北电讯工程学院出版社,1985.119~123,88~89,112,132
6 何述平.图像法处理打点纸带的研究.物理教师,2013,34(1):57~60
7 朱鹤年.物理实验研究.北京:清华大学出版社,1994.106~112
8 许湘苗.奇数项数据的最佳逐差间隔数与误差.物理通报,2013(11):81
9 朱鹤年.基础物理实验教程:物理测量的数据处理与实验设计.北京:高等教育出版社,2003.81~82
10 张波.注意使用条件 慎用二级结论 防止思维惯性.物理教师,2012,33(1):60~62

