梯形电阻网络等效电阻通项公式求法

骆宪武

(长沙市长郡中学 湖南 长沙 410002)

对于二端无限梯形电阻网络的等效电阻，我们通常采用极限法来求解. 所谓极限法，就是先设K个网络元组成二端网络，将其等效电阻记为RK；再连接一个网络元，其等效电阻记为RK+1. 设法找出RK+1与RK之间的递推关系，最后令K→∞，则RK+1与RK就都是所求的由无穷网络元构成的二端网络的等效电阻.RK+1与RK之间的递推关系成为关于等效电阻的一元代数方程，解此方程可得出等效电阻． 但这种做法不够严谨，我们不能无根据地认为，K→∞时，一定有RK+1=RK=R∞的结果.因为只有在证明数列R1,R2,…，RK,…存在极限R∞之后，才有K→∞时，RK+1=RK=R∞的结果.即从严格意义上，我们首先要由RK+1与RK之间的递推关系得出RK的通项式，然后证明{RK}是单调数列且存在极限，最后求出RK的极限，才为电阻网络的等效电阻.因此，由RK+1与RK之间的递推关系得出RK的通项式是关键.笔者在物理竞赛培训中，发现学生从物理和数学的角度，很好地探讨了一个二端无限梯形电阻网络等效电阻RK通项式的求法，加以整理，供大家参考.

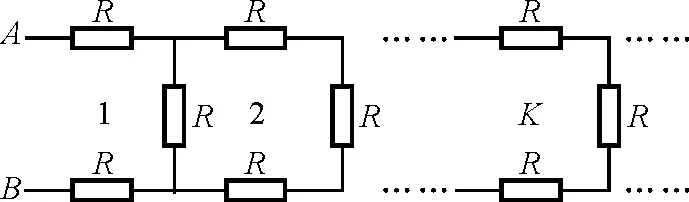
图1

图1所示为一个二端无限梯形电阻网络，它由K→∞个相同的网络元串接而成,每个网络元包含3个相同的电阻R.试求该无限梯形电阻网络等效电阻RK通项式.

1 电流分布法

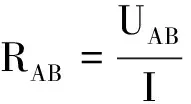
图2

假设电流由A流入，由B流出，由对称性可知，每个单元格上下两电阻中电流相等，电流分布如图2所示. 考察第n个网格，1≤n≤k,n∈N+,i1=I.由基尔霍夫定律得

Rin+R(in-in+1)+Rin-R(in-1-in)=0

化简可得

in+1+in-1=4in

设

in+1-αin=β(in-αin-1)

比较两式有

即α，β为方程x2-4x+1=0的两根.

或

又因为引进的系数α，β地位均等，故in+1-αin与in+1-βin均为等比数列，公比分别为β，α，所以

取n=K,又由初始条件i1=I,则有

再考虑最后第K个单元格有

图33RiK-R(iK-1-iK)=0

所以iK-1=4iK，代入上述方程组有

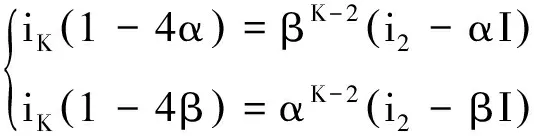
注意到

代入得

对该二端无限梯形电阻网络

UAB=2IR+(I-i2)R=

所以

2 构造数列待定系数法

求数列的通项公式，最为广泛的办法是，把所给的递推关系变形，使之成为某个等差数列或等比数列的形式，于是就可以由此推得所给数列的通项公式．求解的关健在于变形的技巧，而变形的技巧主要在于引进待定系数．其基本原理是递推关系两边加上相同的数或相同性质的量，构造数列的每一项都加上相同的数或相同性质的量，使之成为等差或等比数列．

本题中，由图1可知RK与RK+1之间的关系为

可以将其化简为

令

则上式变为

aKaK+1-3aK+aK+1-2=0

(1)

为了消去常数项，令bK=aK-m，上式变为

bKbK+1-pbK+qbK+1=0

(2)

比较式(1)、(2)，aK，aK+1项的系数相同，有

可得

则式(2)可变为

两边同除bKbK+1得

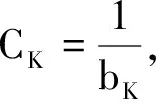
(3)

同理，令DK=CK-T，有

(4)

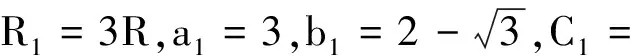
所以

3 不动点法

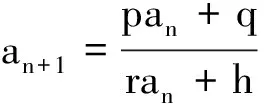
当特征方程有且仅有一个根λ时,分为以下情形：

若a1=λ,则an=λ,n∈N;

n∈N.特别地，当存在n0∈N,使bn0=0时，无穷数列an不存在.

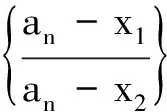
如前述，RK与RK+1之间的递推关系为

令

铜仁市大部年降水量为1 100～1 400毫米，位于梵净山东南侧的凯马、落满一带降水为1 100～1 400毫米，松桃县、江口县、万山区一带为1 150～1 300毫米，印江县和石阡县一带为全区最少区域，降水量1 100～1 150毫米，其中4～9月降水量占75%以上，秋收作物主要生育期雨量相当充沛。

则上式变为

且a1=3.

先求不动点. 为此，令

解得

……

由上K-1个式子累积相乘可得

又由初始条件a1=3，可得

上式变为

代入

得

则RK的通项式为

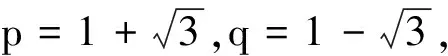
通过对一个二端无限梯形电阻网络等效电阻通项式的求法探讨，学生积极思考，得出几种不同的求法，深化了对物理知识的理解，将所学数学知识灵活加以应用，交流中开阔了视野、提升了能力，正是我们在竞赛培训过程中期许的结果．

参考文献

1 舒幼生，等.物理学难题集萃.北京：高等教育出版社，1999.680～683

2 赵凯华，陈熙谋.电磁学(第二版上下册).北京：高等教育出版社，1991

3 邵建新.梯形电阻网络等效电阻的通项式.物理与工程,2006(4)：29～33