基于线性回归的重力数据三维RMS成像

吉日嘎拉图，鲁光银

(中南大学 地球科学与信息物理学院, 长沙 410083)

0 引言

重力勘探是最早应用在油气勘探领域的地球物理方法，虽然现在逐渐被地震勘探所取代[1]，但是在深部勘探等方面的优势，是其他地球物理勘探方法所无法取代的。而且重力勘探方法能在各种平台上获得大量观测数据，从而在大地构造分区、矿产资源勘查以及基础地质研究提供了重要的地球物理依据[2]，同时也作为其他地球物理勘探方法反演算法中的约束发挥着重要作用[1]。在任何地球物理勘探方法的应用过程中，必须对实际测量异常进行反演解释，重力勘探也不例外，重力数据解释的基本目标就是要得到一个清晰的异常源[3]，而且这也是应用重力勘探的重要环节，常规重力异常反演方法是基于反演理论的、在最小二乘意义下，使目标函数达到最小的线性或者非线性反演[4]。根据重力异常，利用一些统计分析的方法(如地层视密度的解释方法)，来求取异常源的位置和物性参数，大体上也是属于反演问题[5]。但前一种反演方法必须计算非常庞大的数据量，尽管姚常利[6]等学者都提出了相关的解决方法，但是仍然要耗费大量的计算时间。

基于概率统计的数据解释及处理方法，最早是由Spector和Grant提出的[7]，经过不断地发展，在1979年利用统计学的滑窗法处理磁场剖面数据的程序用来进行场源深度估计被发表[8-9]；1981年Chandler[10]利用滑动窗口的方式进行重磁数据的线性回归计算，这也是日后被大家所熟知的重磁异常对应分析[11]；概率成像，最初是由自然电位法的解释方法发展而来，经Patella和Mauriello[12-14]两位学者不断发展，已将该方法应用位场勘探等领域，而且取得了令人满意的结果；Domenico Patella[15]利用概率密度成像方法对维苏威火山地区进行概率密度成像研究，而且提出了联合概率成像；郭良辉，孟晓红[4, 16-19]提出基于相同匹配滤波技术的三维相关成像[20]，并且已将该方法推广到重力梯度数据应用领域。由于梯度数据本身所具有高分辨率的性质，使得重力梯度数据的成像结果要明显好于直接利用重力数据进行成像的结果。对于以上这些基于统计学的反演方法，普遍都具有的一个优势就是即使没有任何先验信息，都可以得到稳定的解释结果[20]。

作者正是受到重磁异常对应分析和重磁概率成像(相关成像)算法的启发，提出了一种基于线性回归的重力数据均方根残差(RMS)成像方法，对地下重力异常源的分布情况进行研究和探索方法。该方法对于重力异常源的位置较为敏感，所以可以用来进行成像分析。

1 方法原理

地下异常源在，水平测区的所产生的重力异常用公式(1)表示：

(1)

其中 G为万有引力常量 G=6.67×10-11m3/(kg·s2)。

借助相关成像[4]的原理，将式(1)进行推广，设置笛卡尔坐标的(x,y)平面在基准面上，z取垂直向下为正，假设测区地下任意点源坐标为(xi,yi,zi)、体积为vi的第i个点质量的剩余密度为σi，则它在测区上任意位置(x,y,z)处的重力异常为：

(2)

根据式(2)，我们将重力异常抽象概括为地下异常体物性参数与几何构造函数[6]的乘积：

Δgi=GσvQ(xi,yi,zi)

(3)

Q(xi,yi,zi)表示地下异常体的几何构造函数：

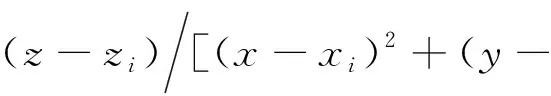
yi)2+(z-zi)2]3/2

(4)

利用一元线性回归的原理，将重力异常表示为：

Δg(x,y,z)=A·Q(xi,yi,zi)+b

(5)

所以地上所测重力异常与地下第i个点所对应的异常源几何构造函数存在着线性的对应关系，在进行线性回归分析之前，必须进行相关性检验，验证是否是存在线性相关性。

对任意一组观测值与几何构造函数，不管是否相关都可以建立一个线性回归方程，这就产生了一个问题，这样得到的线性回归方程是否真的具有线性关系，而且所求的线性回归方程是不是能够反映它们之间的实际关系，因此进行线性之前，必须进行线性相关关系检验[6]。

根据统计学原理[21]，相关系数被定义为式(6)：

(6)

其中 cov(Δg(x,y,z),Q(xi,yi,zi))为二者的协方差；D(Δg(x,y,z))和D(Q(xi,yi,zi))表示其相应的方差。

当满足线性相关性之后，利用最小二乘原理，求解线性回归方程，得到等式(7)所表示的线性回归方程斜率和截距公式：

(7)

根据均方根残差法(RMS)原理，对其进行修正，用相关系数R当作ΔGcalc的权，相关程度越高，拟合程度越接近，才能越接近真实观测值，因此得到了等式(8)加入相关系数R修正后的RMSm，因为相关系数-1≤R≤1，故对于式(8)，只需要寻找局部极值(包括极大值和极小值)就可以准确找到异常源的所处位置。

RMSmodified=

(8)

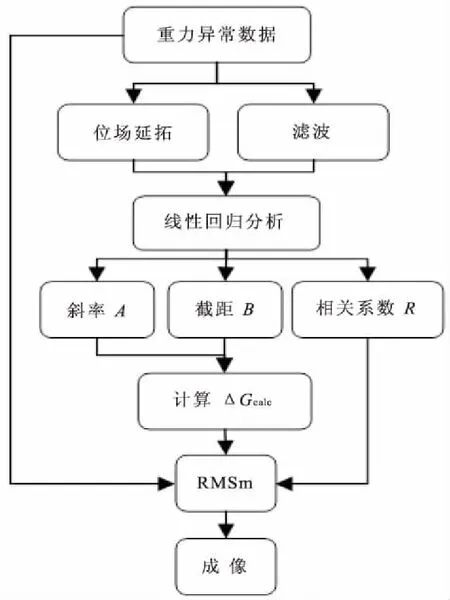
图1 利用线性回归进行场源分析的流程图Fig．1 The flow chart of processing 3-D RMSm imaging

2 基于线性回归的重力数据三维RMS成像

如图1所示的流程已经完整的阐述了利用线性回归方法进行重力异常场源分析的工作流程。需要注意的是，此处的重力异常数据是经过布格校正和网格化的。在经过位场延拓和相关的滤波算法，可以在一定程度上提高沿深度方向上的分辨率[4]。

在计算时，首先要对地下空间进行剖分计算，为了方便计算，一般选择利用等间距的网格剖分方法，将地下空间剖分成均匀网格。此时假设地下空间中必定存在某一些点是满足等式(5)的，所以利用公式(6)、公式(7)、公式(8)由浅到深的逐层进行计算，最后利用RMSm的数据进行成像。

3 算例分析

为了研究该方法的具体表现，我们利用两个密度为0.5 g/cm3的异常体，设置在地面以下100 m处的位置如 图 2所示。图3(a)为测网100×100，纵横网格间距各为30 m的平面网格上的合成重力异常在异常源正上方，即y=1500 m处的剖面数据，而图3(c)则是在原始数据上添加了20%高斯随机噪声。利用式(6)、式(7)、式(8)对整个数据空间进行计算得到图3(b)、(d)。

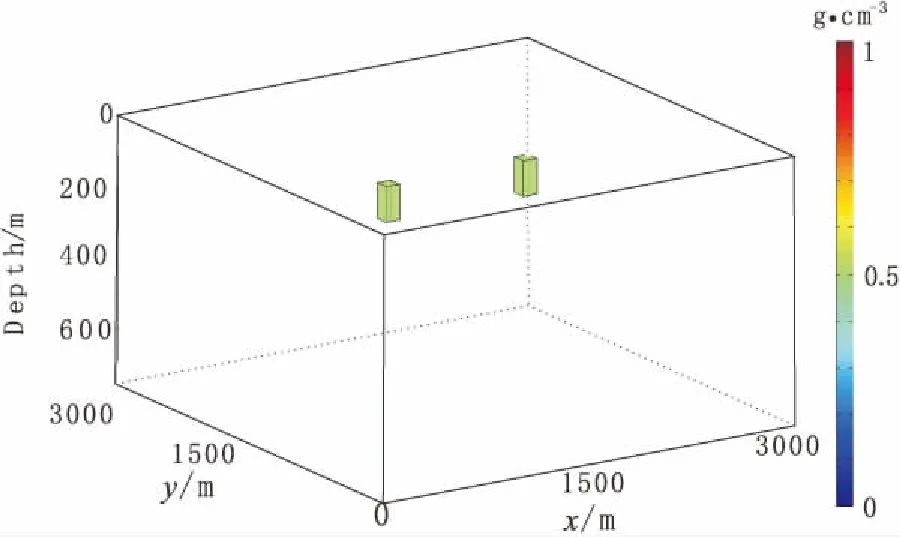
图2 组合模型立体图Fig．2 Perspective of 3D model consisting of two blocks

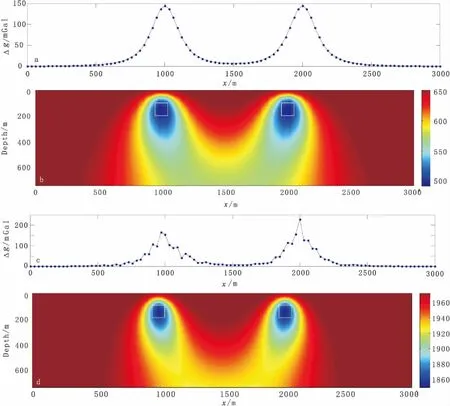
图3 模型RMSm切片图及模型的重力异常Fig．3 The slice maps of the synthetic model and the profiles of its gravity anomalies(a)重力数据在y=1500 m处的剖面; (b)在y=1500 m处RMSm 深度切片 ;(c) 添加了20%高斯随机噪声的重力数据在y=1500 m处的剖面;(d) 添加噪声之后的重力数据在y=1500 m处RMSm 深度切片，白色虚线框是实际异常源的真实轮廓

图3(d)是y=1500 m处RMSm成像结果。从图3可以看出，本文方法所估算出的异常源位置与白色虚线框所标示出的异常源的实际位置非常吻合，所以本文所提出的方法在理论上是有效的。为了说明本算法对于噪声的稳健性，利用添加20%随机高斯噪声的合成重力数据进行验证，如图3(c)所示。图3(d)即为添加噪声之后所得的y=1500 m处RMSm成像结果，从图中可知，该算法具有良好的抗噪性能。

所以从以上算例分析中发现，本文所提出的成像方法对于异常源真实位置的反映是有效的且准确的，而且具有良好的抗噪性能。

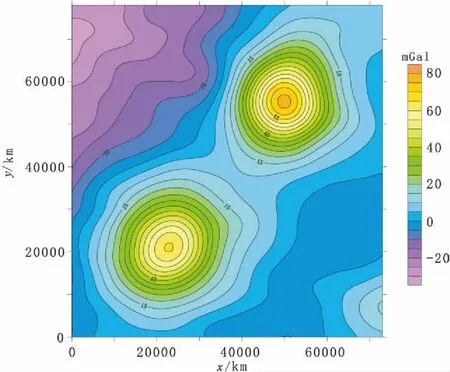
图4 某地实测的布格重力异常的等值线填充图Fig．4 The contour map of the measured bouguer gravity anomaly in a certain region

4 实测资料计算

图4是某地地面重力测量所得的布格重力异常的等值线图，测区范围为73 km×73 km，平面数据网格为100×100，横纵网格间距为730 m，对其进行线性回归的分析并计算RMSm，成像深度大概为0 km～18 km，深度步长为720 m，对其RMSm结果进行三维切片成图，如图5所示，图中白色标记为异常位置，而且极大值正好对应了负重力异常，而图中两处极小值则对应了两处正重力异常，图5的计算结果不仅定性地标记异常源的赋存范围，而且也确定了异常源的深度，因此基于线性回归的重力场源分析的成像结果，将为测区的地质解释提供参考。

图5 该实测异常计算后得到的相关系数的三维切片Fig．5 Three-dimensional slice maps of the intercept related to the measured bouguer gravity anomaly

5 结论

在概率成像和重磁异常对应分析的基础上，提出了一种全新的基于线性回归的重力数据三维RMS成像算法。该成像算法具有方法简单，分辨率高，抗噪性能强等优点，而且在没有任何先验信息约束的情况下可以得到稳定的计算结果。模型算例和实测数据验证分析表明，本文所提出的算法可以有效的定位地下重力异常源的位置和赋存范围

参考文献：

[1] NABIGHIAN M N, ANDER M E, GRAUCH V J S, et al. 75th Anniversary: Historical development of the gravity method in exploration[J]. Geophysics,2005, 70(6): 63N-89N.

[2] 管志宁，郝天珧. 21 世纪重力与磁法勘探的展望[J]. 地球物理学进展,2002, 17(2): 237-244.

[3] SILVA DIAS F J, BARBOSA V C, SILVA J B. 3D gravity inversion through an adaptive-learning procedure[J]. Geophysics,2009, 74(3): 19-121.

[4] 郭良辉，孟小红，石磊，等. 重力和重力梯度数据三维相关成像[J]. 地球物理学报,2009, 52(4): 1098-1106.

[5] 曾华霖. 重力场与重力勘探[M]. 北京: 地质出版社, 2005.

[6] 姚长利，郝天珧，管志宁，等. 重磁遗传算法三维反演中高速计算及有效存储方法技术[J]. 地球物理学报,2003, 46(2):252-258.

[7] NABIGHIAN M N, GRAUCH V, HANSEN R O, et al. The historical development of the magnetic method in exploration[J]. Geophysics,2005, 70(6): 33N-61N.

[8] BLAKELY R J, HASSANZADEH S. Estimation of depth to magnetic source using maximum entropy power spectra, with application to the Peru-Chile Trench[J]. Nazca Plate. 1981: 667-682.

[9] PHILLIPS J D. ADEPT: a program to estimate depth to magnetic basement from sampled magnetic profiles[M]. US Geological Survey, 1978.

[10] CHANDLER V W, KOSKI J S, HINZE W J, et al. Analysis of multisource gravity and magnetic anomaly data sets by moving-window application of Poisson’s theorem[J]. Geophysics,1981, 46(1): 30-39.

[11] 管志宁. 地磁场与磁力勘探[M]. 北京: 地质出版社, 2005.

[12] MAURIELLO P, PATELLA D. Localization of magnetic sources underground by a data adaptive tomographic scanner[J]. arXiv preprint physics/0511192,2005.

[13] MAURIELLO P, PATELLA D. Imaging polar and dipolar sources of geophysical anomalies by probability tomography. Part II: Application to the Vesuvius volcanic area[J]. arXiv preprint physics/0602057,2006.

[14] ALAIA R, PATELLA D, MAURIELLO P. Imaging multipole gravity anomaly sources by 3D probability tomography[J]. Journal of Geophysics and Engineering,2009, 6(3): 298-310.

[15] IULIANO T, MAURIELLO P, PATELLA D. Looking inside Mount Vesuvius by potential fields integrated probability tomographies[J]. Journal of Volcanology and Geothermal Research,2002, 113(3): 363-378.

[16] CHEN Z, MENG X, GUO L, et al. GICUDA: A parallel program for 3D correlation imaging of large scale gravity and gravity gradiometry data on graphics processing units with CUDA[J]. Computers & Geosciences,2012，46:119-128.

[17] 郭良辉，孟小红，石磊. 磁异常 ΔT三维相关成像[J]. 地球物理学报,2010, 53(2):435-441.

[18] GUO L, MENG X, SHI L. 3D correlation imaging of the vertical gradient of gravity data[J]. Journal of Geophysics and Engineering, 2011, 8(1): 6-12.

[19] GUO L, SHI L, MENG X. 3D correlation imaging of magnetic total field anomaly and its vertical gradient[J]. Journal of Geophysics and Engineering, 2011, 8(2): 287-293.

[20] FEDI M, PILKINGTON M. Understanding imaging methods for potential field data[J]. Geophysics, 2012, 77(1): G13-G24.

[21] 韩旭里，王家宝，陈亚力，等. 大学数学教程-概率论与数理统计[M]. 北京：科学出版社, 2006.