用阻抗相位识别二维音频大地电磁垂向异常

周 军，王闻文，刘 红，李东北，李英勇

(1.成都理工大学 地球探测与信息技术教育部重点实验室, 成都 610059; 2.成都奥塔科技有限公司, 成都 610091; 3.重庆一三六地质队, 重庆 401147; 4.四川省地质工程勘察院, 成都 610072)

0 引言

近年来，音频大地电磁测深法(AMT)的应用日益广泛,提高其实际勘探效果成为研究者关注的焦点。在实际工作中，浅地表的电性不均匀体将引起测量数据的静态位移，这严重影响了AMT资料的质量，增加了数据解释的多解性。为减少或压制静位移对AMT数据的影响，提高数据解释的可靠性，国内外研究者开展了大量的研究工作，并提出了许多压制静位移的方法[1,5-9]。然而在AMT的勘探中，由陡立岩体或断裂引起的垂向电性异常也大量存在，这类异常在视电阻率断面中的变化特性与静态位移引起的异常变化在形态上极为相似，这无疑增加了静校正的难度。实际工作中往往是静态位移现象和垂向电性异常带同时存在，而目前的静校正方法通常只考虑横向的视电阻率的变化，很难做到在充分压制静位移的同时突出真实垂向异常。因此，静态位移校正问题还需要进一步研究。

利用其他物探方法的测量数据开展音频大地电磁静校正研究是一条途径[7-8]，但与之相伴的是勘探成本的增加和工作效率的降低。理论研究表明，当区域电性结构可以近似为二维模型时，静态位移对大地电磁阻抗相位的影响较小[1-2，4]，而垂向异常体则可能引起观测到的阻抗相位发生变化。因此，利用阻抗相位的特性开展大地电磁资料综合解释，有助于在实际工作中区分静态位移与真实垂向电性异常，从而提高AMT数据解释的可靠性。

1 阻抗相位的性质

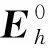
(1)

考虑二维地电模型，设测量轴x、y与电性主轴方位一致，区域构造走向为x方向。此时，大地电磁阻抗张量可以表示为：

当地电模型浅部存在局部电性不均匀体时，观测到的电、磁场水平分量将在二维区域场的基础上产生畸变

(2)

(3)

式中I为单位矩阵；P与Q为联系水平方向畸变场与区域场的张量。其中电畸变张量P源于不均匀体界面的电荷积累，而磁畸变张量Q则源于电流沟道效应对磁场的影响。

根据大地电磁阻抗张量与电、磁场的关系，可以得到电、磁场全畸变的阻抗张量：

Z=(I+P)Z0aa(I+QZ0)-1

(4)

当不均匀体的垂向尺度足够小，且观测频率足够低时，P与Q中的元素是与频率无关的实常数，其大小与不均匀体两侧的电性差异有关。仅考虑电场畸变时，式(4)中的电场畸变部分(I+P)只引起相关频率阻抗幅值的变化，但不影响阻抗相位。当需要同时考虑磁场变化时，由于式(4)中的磁场畸变部分(I+QZ0)-1含有相关频率的区域阻抗(与频率相关的复数)，因此观测的阻抗幅值与相位都将发生变化。随着观测频率的降低，磁场畸变的影响将迅速减弱[2]，换而言之，磁场畸变主要发生在高频阻抗数据中，对低频数据则影响较小。

1.1 静态位移中的阻抗相位响应

当局部不均匀体的尺度远小于观测电磁波频率的趋肤深度时，测量数据将发生静态位移[1]。此时磁场畸变部分(I+QZ0)-1将趋向于单位矩阵I，即静态位移属于电场畸变，与磁畸变无关。观测阻抗张量表示为

Z=(I+P)Z0

(5)

在实际工作中，浅部不均匀体的尺度具有一定变化，可能会引起较高频阻抗发生电、磁场全畸变。考虑到磁场畸变随着频率的降低而迅速减弱，对于低频段的AMT数据而言上式仍成立。

1.1.1 三维/二维模型

当区域地电模型为二维结构，而浅部不均匀体为三维结构时，静位移影响下的阻抗张量具有如下形式：

(6)

由于浅部电性不均匀体的影响，观测到的阻抗张量中的辅助阻抗Zxx与Zyy不再为零。考虑视电阻率ρ与阻抗相位θ的定义

畸变后的AMT数据与区域AMT数据(以上标“0”表示)的对比关系如下

(7)

由此可见，在三维浅表不均匀体的影响下，两个模式下的视电阻率曲线都将在双对数坐标下发生平移，即所谓的静态位移，而阻抗相位则不受静态位移畸变的影响。

1.1.2 二维模型

当浅部电性不均匀体蜕化为二维，其走向沿x方向，与区域构造方向一致。此时，畸变张量中Pxx、Pxy与Pyx均为零。二维静态位移畸变下的阻抗张量可以表示为式(8)。

(8)

此时阻抗张量中的两个辅助阻抗恒为零，畸变后的AMT数据与区域AMT数据(以上标“0”表示)之间联系如式(9)所示。

(9)

式(9)说明在二维地电模型中，静态位移对AMT数据的影响仅限于TM模式视电阻率曲线，双对数坐标下该曲线将在电阻率轴上平移。

综合以上分析可知，当地下介质可以近似为二维结构时，静位移会造成视电阻率曲线在双对数坐标下的平移，而对阻抗相位资料则基本无影响。

另外，当区域地电模型表现为三维结构时，区域阻抗张量的四个元素均不为零。此时分析式(5)可知，静位移将导致视电阻率曲线和阻抗相位曲线在形态上发生变化。

1.2 二维垂向异常影响下的相位响应

考虑地电模型中存在二维垂向异常体。由于其深部界面两侧的电性差异，将会导致低频段的AMT阻抗相位与视电阻率在横向上发生变化。此时，也可以用式(4)来描述二维垂向异常体对阻抗张量的影响。但是必须注意的是，相对于观测电磁波频率而言，二维垂向异常体在纵向延伸尺度较大，因此畸变张量P与Q的物理意义发生了改变，P与Q表征了一定深度范围的电性异常体对相应频段电、磁场的影响，其元素是与频率有关的复数。由分析式(4)可知，由于在测量区域内叠加了二维垂向异常体，将造成阻抗张量幅值与相位同时发生改变。

1.3 基于阻抗相位的解释方法

由以上论述可知，当地电模型可以近似为二维模型时，静位移和真实垂向异常中的阻抗相位响应存在差异，这将有助于在实际工作中对垂向异常进行定性分析。但是必须注意到，以上讨论是基于浅表的不均匀体和由深部贯穿至地表的异常体这两种极限情况。实际上当不均匀体在纵向上具有一定的延伸时，也可能导致较低频段的数据发生电、磁场全畸变，并引起相位变化，此时很难利用原始相位数据对异常直接进行精细解释，可以利用相位拟合度对反演结果进行解释。在反演中采用均匀半空间作为初始模型，避免初始模型中带入静位移，可以得到对垂向异常反映更为客观的反演结果，而阻抗相位的拟合程度将作为判断反演结果是否合理的依据。另外，如果在反演中加入相位，考虑到其与阻抗、视电阻率的关系

log(Z)=log(ρ)/2+iθ+log(ωμ)/2

得到联合反演中的数据方差函数为式(10)。

(10)

式中N表示总频点数量；下标a与c分别表示实测数据与理论数据。

2 模型计算

如图1所示建立地电模型，该模型同时包含了静态位移与真实垂向异常。模型中地电断面长度为4 km，深度为1 km，背景电阻率为500 Ω·m。在模型横向距离1 km、3 km处分别存在宽度为0.2 km，电阻率为50 Ω·m的低阻体。其中1 km处低阻体仅分布于近地表，3 km处的低阻体则是由深部贯穿至地表。采用矩形网格剖分对该模型进行了二维有限元正演。其中横、纵向网格数量为80×60，在100 kHz～0.1 Hz范围内按对数等间距取60个计算频点。

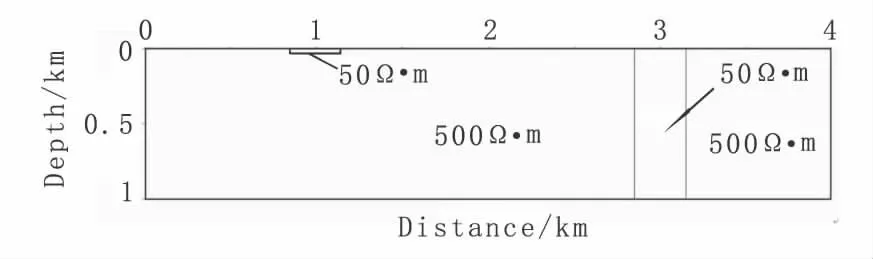
图1 垂向异常带地电模型Fig．1 Vertical geoelectric anomalies model

图2为模型的二维正演结果。考虑到二维地电结构下静态位移的特点，在此仅对TM模式数据的响应特性进行分析。TM模式视电阻率拟断面中，在1 km及3 km处分别出现了相似的纵向电阻率异常带。反观阻抗相位拟断面，剖面1 km处仅在高频部分出现异常，在低频部分则无相位异常。这表明浅部不均匀体引起的电、磁场变化导致了高频阻抗相位的变化，而低频段阻抗相位则不受其影响。在剖面3 km处出现了全频段的阻抗相位高异常，这是二维垂向电性异常体在相位拟断面中的客观反映。

采用NLCG方法对上述模型的TM模式视电阻率和阻抗相位进行了联合反演。反演中采用电阻率为200 Ω·m的半空间初始模型，迭代20次，平均相位误差小于2/频点。从相位拟合误差可以判断，反演结果(图3)反映的垂向异常电性分布较为可靠。

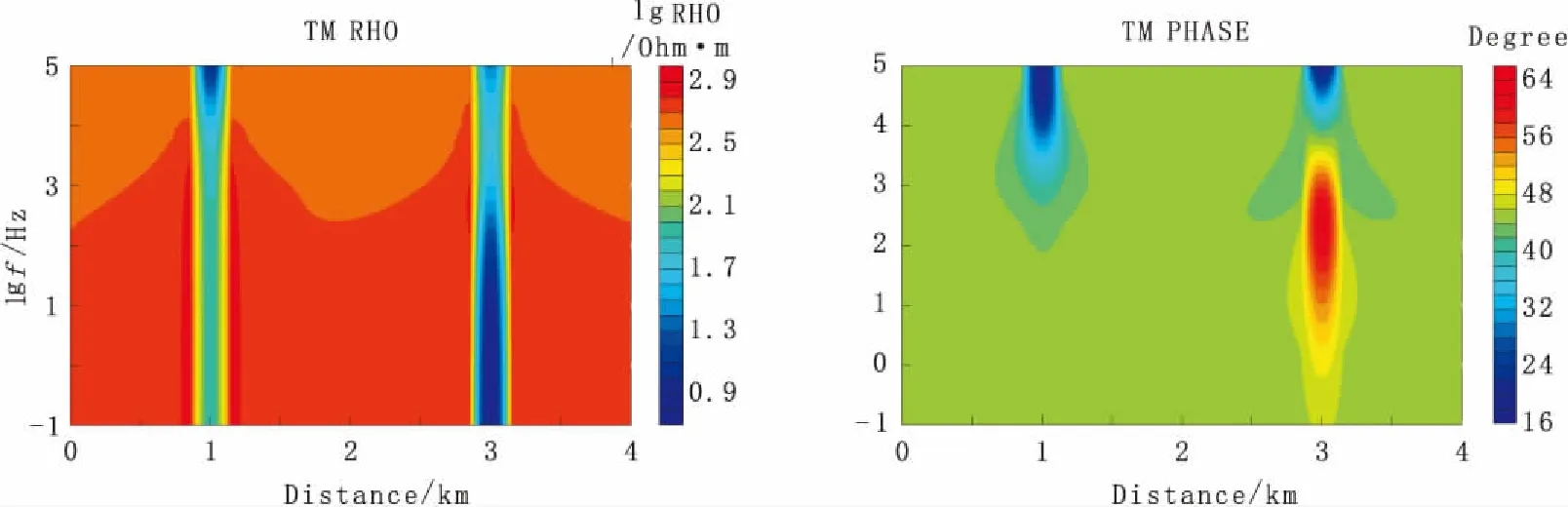
图2 垂向地电异常二维正演响应Fig．2 2D forward modeling of vertical geoelectric anomalies

图3 二维NLCG反演结果Fig．3 Result of 2D NLCG inversion

图5 11线实测视电阻率与阻抗相位拟断面Fig．5 Apparent resistivity and impedance phase pseudosections of line 11

3 应用实例

西南某煤矿位于灰岩及第四系出露地区，区内断裂及岩溶发育，对矿山安全造成影响。为查清矿区内隐伏断裂及岩溶的发育情况，在该煤矿及周边区域开展了AMT工作。其中11号测线全长560 m，按20 m～40 m点距共计布设21个测点。作为目标体的断裂及岩溶在充水后，其电性特征将反映为相对低阻。可推断出，本区的工程地球物理模型为在高阻中寻找低阻异常。

根据静态位移的特点，利用阻抗相位变化识别垂向异常时，要求测区地电模型必须能近似为二维结构。考虑到二维偏离度取值可能较大，不利于图形显示。在此采用二维偏离角进行维数解释，该参数是二维偏离度的正弦值， 可由式(11)表示

Angleskew=arcsin(skew2D)

(11)

利用式(11)将取值范围限定在0°～90°之间。在二维偏离角的图示中，以角度值小于30°作为二维近似的标准。图4为11号剖面的二维偏离电性结构。

图4 11线二维偏离角拟断面Fig．4 2D skew angle pseudosection of line 11

根据图4展示的结果可以判断，测区电性结构可以近似为二维模型。此时可以根据阻抗相位的变化特性判断该地区视电阻率剖面中出现的垂向异常是否为真实垂向电性异常体引起。

采用相位张量分解方法，得到该剖面的TE与TM数据。图5为11线TM模式视电阻率与视相位拟断面，在剖面0.2 km处存在低电阻率异常带，与之相对应的是该处还存在全频段的高相位异常。根据图5可以定性判断，11号测线0.2 km附近的低阻异常应该为真实存在的垂向电性异常体引起。因此，不宜对该异常区的视电阻率曲线进行太大尺度的静校正。

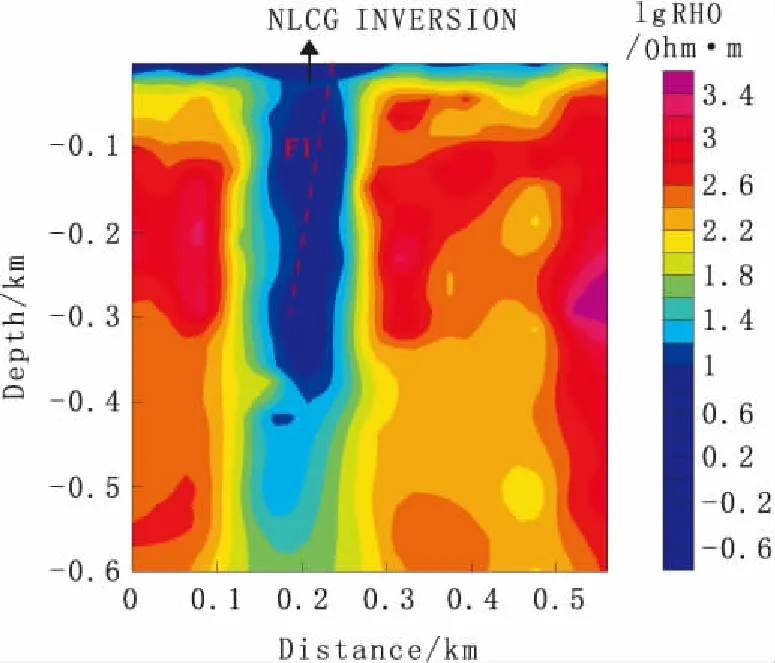
图6 11线NLCG联合反演结果Fig．6 NLCG joint inversion result of line 11

为保证反演解释结果的可靠性，利用阻抗相位和视电阻率NLCG联合反演了11线TM模式数据。采用均匀半空间模型作为初始模型，模型电阻率由剔除飞点后的实测视电阻率均值得到。反演迭代36次，异常区平均相位误差小于3.8°/频点。结合对该区的地质调查成果，推断该垂向低阻异常带是由陡立的破碎带所引起，这与后期钻井资料所揭示的地下实际情况相符。

4 结论

阻抗相位对识别和解释二维垂向异常具有积极意义。设定合理的反演初始模型，避免其带入静态位移，有利于提高反演结果对垂向异常反映的客观性，而垂向异常区的相位数据拟合程度可以作为异常解释合理性的判断依据。

由于受到初始模型的限制，该解释方法对复杂地质条件下的微弱异常识别效果可能有限，此时有必要结合其他解释方法进行综合分析。

参考文献：

[1] 王家映. 关于大地电磁的静校正问题[J]. 地质科技情报,1992,11(1):69-76.

[2] 晋光文,孔祥儒.大地电磁阻抗张量的畸变与分解[M].北京:地震出版社,2006.

[3] 晋光文.大地电磁阻抗相位资料的特点和应用[J].地震地质,1988,10(4):159-168.

[4] SIMPSON F, BAHR K. Practical magnetotellurics[M]. Cambridge University Press, 2005.

[5] BEAMLSH D, TRAVASSOS J M. A study of static of shift removal from magnetotelluric data[J]. Journal ofApplied Geophysics, 1992, 29(2): 157-178.

[6] JONES A G. Static shift of magnetotelluric data and its removal in a sedimentary basin environment[J]. Geophysics, 1988, 53(7):967-978.

[7] STERNBERG B K, WASHBURNE J C, PELLERIN L. Correction for the static shift in magnetotellurics using transient electromagnetic soundings[J]. Geophysics, 1988, 53(11):1459-1468.

[8] PELLERIN L, HOHMANN G W. Transient electromagnetic inversion: A remedy for magnetotelluric static shifts[J]. Geophysics, 1990, 55(9):1242-1250.

[9] TOURNERIE B, CHOUTEAU M, MARCOTTE D. Magnetotelluric static shift: Estimation and removal using the cokriging method[J]. Geophysics, 2006, 72(1): 25-34.