基于L1范数的多次波自适应减方法及应用分析

熊繁升， 黄新武， 高孝巧， 蔡双霜， 雷海波， 何 江

(中国地质大学 工程技术学院，北京 100083)

0 引言

多次波问题在地震勘探中普遍存在，如果不能对多次波进行有效地压制，则将影响地震成像的真实性和可靠性，并干扰对有效波的识别，从而导致速度分析、叠前及叠后偏移的极大困难。因此，对多次波压制方法及应用进行研究不仅具有重要理论意义，而且有一定实际意义和应用价值。针对多次波压制问题，不同学者提出了不同的方法，可分为两个主要类别：①基于一次波和多次波在空间上特性差异的去噪方法；②基于多次波的周期性和可预测性的去噪方法[1]。

由Verschuur等[2-4]提出的自由表面相关多次波压制(SRME)方法是多次波压制技术的突破，亦是目前压制多次波方法和技术的主流。SRME方法使用一个匹配算子将通过反馈迭代法[1]预测得到的地震记录的多次波模型从输入数据中减去，其要求预测的多次波与实际数据中的多次波匹配较好，否则将直接影响多次波的压制效果甚至损害有效波，因此做好多次波自适应减对其压制效果十分重要。

目前常用的多次波自适应减方法有L2范数多次波自适应减方法。该方法基于剩余能量最小原则，即有效波与多次波正交这一假设，而实际的地震数据并不是都能满足该假设。同时，L2范数对于误差较大的情况即出现异常值较为敏感[5]，因此应用此方法有可能会导致大的多次波剩余，或者衰减有效波的能量。L1范数对于出现较大异常值时也能给出稳定解[5-6]，且无须满足有效波与多次波正交这一条件,从而可以利用L1范数来代替L2范数建立多次波自适应匹配滤波器。

作者采用基于迭代重加权最小二乘法(IRLS算法)的混合L1/L2范数来近似L1范数解，该方法能有效地逼近Lp范数[6]。作者先就该方法的基本原理进行阐述，然后通过对复杂海底模型、Pluto 1.5模型数据和实际地震数据进行多次波压制处理，并将处理结果与L2范数多次波自适应减方法进行比较。此外还对影响多次波压制效果的若干因素进行了简要分析。

1 方法原理

1.1 基于L2范数的多次波自适应减方法

目前常用的多次波自适应减方法基于最小二乘准则，即L2范数多次波自适应减方法，其目标是使输入数据与滤波后的多次波之差的平方和即输出能量E(s)达到最小[1]。L2范数多次波自适应减方法的目标函数为式(1)。

(1)

式中d为原始含多次波地震记录；M为由反馈迭代法得到的预测多次波模型的矩阵形式；s为自适应滤波算子。由于实际的地震数据并不是都能满足输出能量E(s)最小，即有效波与多次波正交，因此应用此方法有可能会导致大的多次波剩余，或者衰减有效波的能量。

1.2 基于L1范数的多次波自适应减方法

对于L1范数解，则不需要满足有效波与多次波正交。基于L1范数的多次波自适应减方法的目标函数为式(2)[7]：

E(s)=|d-Ms|1

(2)

式中 各符号意义同式(1)。

秦铁崖痛饮一杯，继续道：“秦某就不同了。缉拿真凶、抓捕恶徒是我的职责，只要能抓到真凶，自己落败受伤也在所不惜，对手是死是活更无足轻重，只要能不辱使命，就算完胜。再说，我是公门中人，受伤可以休养，名正言顺。年年办案，月月追凶，我也会厌烦，也会烦躁，暗地里也会发牢骚：这苦差，什么时候才是尽头？这营生，什么时候才能歇一歇？幸好，每过一段时期，我就会受点小伤，正好歇一歇，让狂躁厌烦之心安顿一下，才不至发疯。更妙的是，受伤静养，正好有空闲盘点前阶段办案得失，思考对敌手段中的疏漏。”

由式(2)可以看出基于L1范数多次波自适应减方法的目标函数E(s)的一阶导数不是处处连续，因此不能运用高效的Levinson递推算法确定滤波器，故在求解的过程中会带来一定的困难。公式(2)中的最优滤波器s需要用非线性反演方法来确定[1]。

由于L1范数的目标函数一阶导数不连续，为此人们提出了求解L1范数最小值的线性方法，比如Huber范数方法[8-9]。本文采用基于迭代重加权最小二乘算法(IRLS算法)的混合L1/ L2范数的方法来近似得到L1范数解。IRLS算法采用迭代过程求解一系列加权最小二乘问题，并在每次迭代过程中按照一定规则调整权重，以逐步逼近最优解，其具有收敛速度快的特点；同时，采用此方法可将非线性问题的求解，转化为分段线性问题的求解[6,10]。此方法是将L1范数转化为加权后的L2范数，其目标函数为式(3)

(3)

式中W为加权矩阵，是对角矩阵，主对角线上的元素根据式(4)确定[17]：

(4)

其中ri为第i个采样点去除多次波后的残差，即

r=d-Ms

(5)

在式(4)中，ε是一个非常重要的先验值参数，其大小对加权矩阵主对角线上元素数值有影响，进而影响求解滤波算子s时方程组的系数矩阵。由式(4)可知，加权矩阵W中元素的数值与残差ri有关，由式(5)知残差ri中又包含算子s，故式(3)是非线性的，不能用一般线性方法求解。

由式(4)和式(5)可知：给定ε，若残差ri小于ε，二者相差越大，wii越大且wii越接近“1”，则矩阵W接近于单位对角矩阵；当残差ri趋于零时，即剩余能量最小，式(3)等价于式(1)，即此时的解相当于L2范数解；若残差ri大于ε，二者相差越大，式(4)近似等于(ri/ε)-1/2，即此时的解为L1范数解。通过合适的ε的可以实现L1范数与L2范数的平滑过渡[10-11]。ε通常取值如下[11-12]：

(6)

对式(3)中的s求导并令其等于零并化简，根据基于IRLS算法的混合L1/L2范数准则，求解使目标函数E(s)最小可转化为求解以下含滤波算子s的方程组：

MTWTWMs=MTWTWd

(7)

记矩阵A=MTWTWM，向量b=MTWTWd。为防止系数矩阵A成为奇异矩阵，在矩阵A的每个主对角线元素加上一个阻尼系数，则式(7)转化为下式：

(A+λI)s=b

(8)

式中λ为阻尼系数，一般取0.001～0.002。

对于式(8)的求解，可采用牛顿迭代法，李学聪等[13]采用了直接迭代法，这里采用共轭梯度算法进行求解，因其收敛速度较快，且得到的解较为稳定。基于IRLS算法的混合L1/L2范数单道多次波自适应减方法的实现过程简单描述如下：首先设定IRLS算法、共轭梯度法的求解精度、最大迭代次数(以防止解不收敛)以及滤波算子s的长度；根据SRME的迭代实现方法原理，得到预测的多次波模型；其次设定各初始值并代入式(8)由共轭梯度法求解得到滤波算子s；然后计算当前剩余误差r并判断是否达到精度要求；最后如果满足剩余误差r满足精度要求，则输出该道处理结果做迭代处理，不满足，则修正权矩阵的数值重复求解。整个实现过程如图1所示。

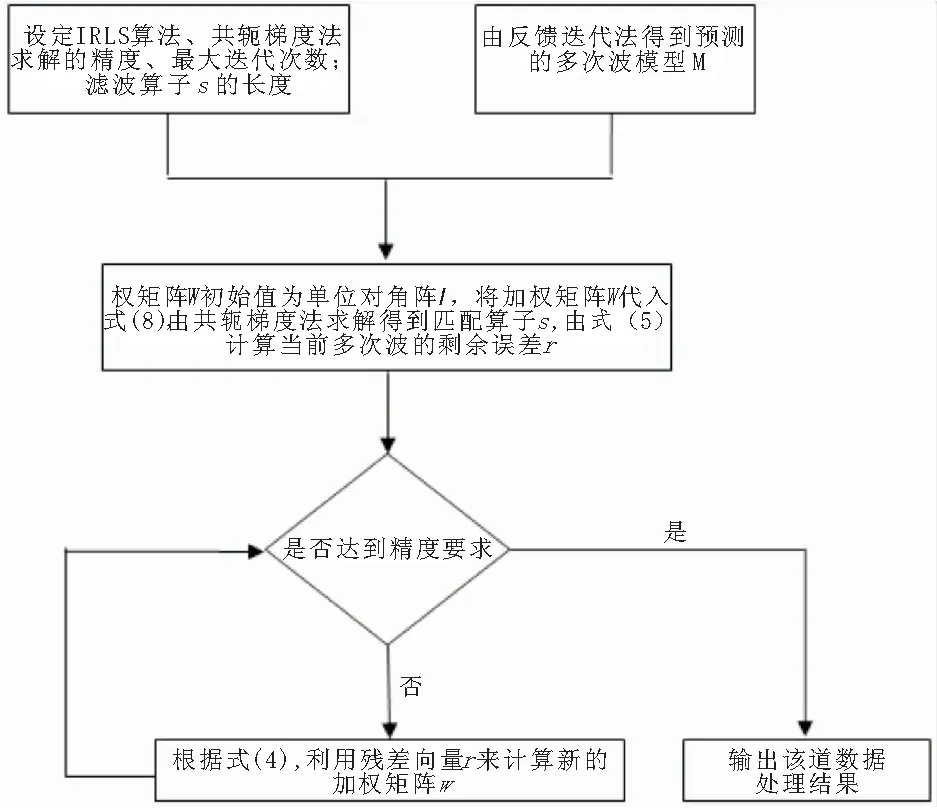
图1 混合L1/L2范数多次波自适应减方法流程图Fig．1 Flow chart of adaptive multiple subtraction using hybrid L1/L2 norm

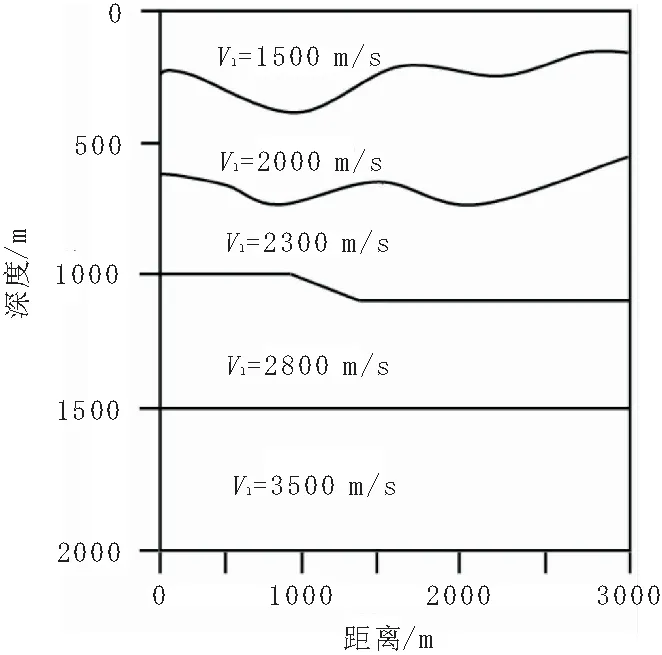
图2 模型一的介质模型Fig．2 The medium model of model 1

2 实例分析

将基于L1范数的多次波自适应减方法应用于两个模型数据和实际地震数据，分析多次波压制效果，并与L2范数多次波自适应减方法作比较。

2.1 模型一

模型一为一复杂海洋地质模型，海底及其下伏地层界面横向起伏较大(图2)，采用声波方程的有限差分法产生人工合成地震记录，分别采用吸收和反射边界条件处理模型边界[14-16]。由于产生多次波的介质系统较为复杂，多次波在横向上的变化较大，故此模型可有效检验多次波压制方法。本数据共141炮，每炮101道，每道501个采样点，4 ms采样。

图3(a)为第1、第30、第60、第90、第125炮共五炮原始含多次波地震记录，可以看出，多次波形式较复杂，且部分多次波与有效波重叠较大。为使L2范数和L1范数多次波自适应减方法具有可比性，两者算子长度均取15个采样点，分相同的两个时窗进行单道处理，在第一个时窗内仅处理一阶多次波；同时在L1范数多次波自适应减方法中，共轭梯度法与IRLS算法的控制精度均设为10-3、最大迭代次数均为100。由图3(b)、(c)、(d)可以看出，采用L2范数多次波自适应减方法虽然压制了部分多次波，但同时引入了一些干扰波；而采用L1范数多次波自适应减方法在多炮记录和零炮检距剖面上多次波的大部分能量均已得到有效压制，具有较强的适应性，且有效波和多次波重叠在一起时，也能获得较好地压制效果。在零炮检距剖面(图4)可以看出，箭头所指示的多次波L1范数自适应减方法较L2范数自适应减方法压制效果好。

2.2 模型二

SMARRT Pluto1.5模型数据是检验多次波压制的一套标准数据。作者选取部分Pluto1.5模型数据测试，共500炮，每炮含200道，每道601个采样点。图5(a)为Pluto 1.5模型的第1、第200、第400炮共三炮原始地震记录。由于该模型较复杂，一阶多次波能量较强且原始数据中存在有效波与多次波交叉的情况。对本数据处理时，L2范数与L1范数的多次波自适应减方法的算子长度均取20个采样点，分相同的两个时窗进行单道处理，在第一个时窗内只处理一阶多次波，迭代3次；在L1范数的多次波自适应减方法中，共轭梯度法和IRLS算法的控制精度均为10-3、最大迭代次数均设为100。图5(b)为L2范数多次波自适应减结果，可以看到，对一阶多次波L2范数自适应减方法压制效果较好，但同时损害了有效波；而基于L1范数自适应减方法减去后不仅多次波的压制较为干净，且有效波能量保护得较好。由图6也可以看到，L2范数自适应减方法与L1范数自适应减方法相比有更大的多次波剩余。

2.3 实际地震数据

这里选取一个单边放炮的二维实际海洋地震数据进行多次波的压制处理，以进一步验证此方法的正确性和适用性。本数据炮点距为50 m，检波点距为25 m，最小炮检距为 200 m，采用插值方法重构近偏移距地震道，对所缺失的八个地震道进行外推重建。图7(a)为预处理及近炮检距数据重建后三炮原始记录，由图7(a)可见，此数据多次波能量较强，且其表现形式复杂，部分多次波和有效波叠加在一起，既有一阶多次波，还有高阶多次波；另外，还有层间多次波。在本次处理中，L2范数和L1范数多次波自适应减方法的算子长度均取25个采样点，分相同时窗进行单道处理，迭代3次；在L1范数多次波自适应减方法中，共轭梯度法和IRLS算法的控制精度均设为10-3、最大迭代次数均设为100。图7为压制多次波前后炮集记录对比图，重建后的数据含有最小偏移距。图8为压制多次波前后最小炮检距剖面对比图，可以看到，箭头所指示处的多次波由L2范数多次波自适应减方法处理之后仍匹配不足，尤其是一阶多次波；而基于L1范数自适应减方法处理后大部分多次波被压制，且有效波的大部分能量保护得较好。

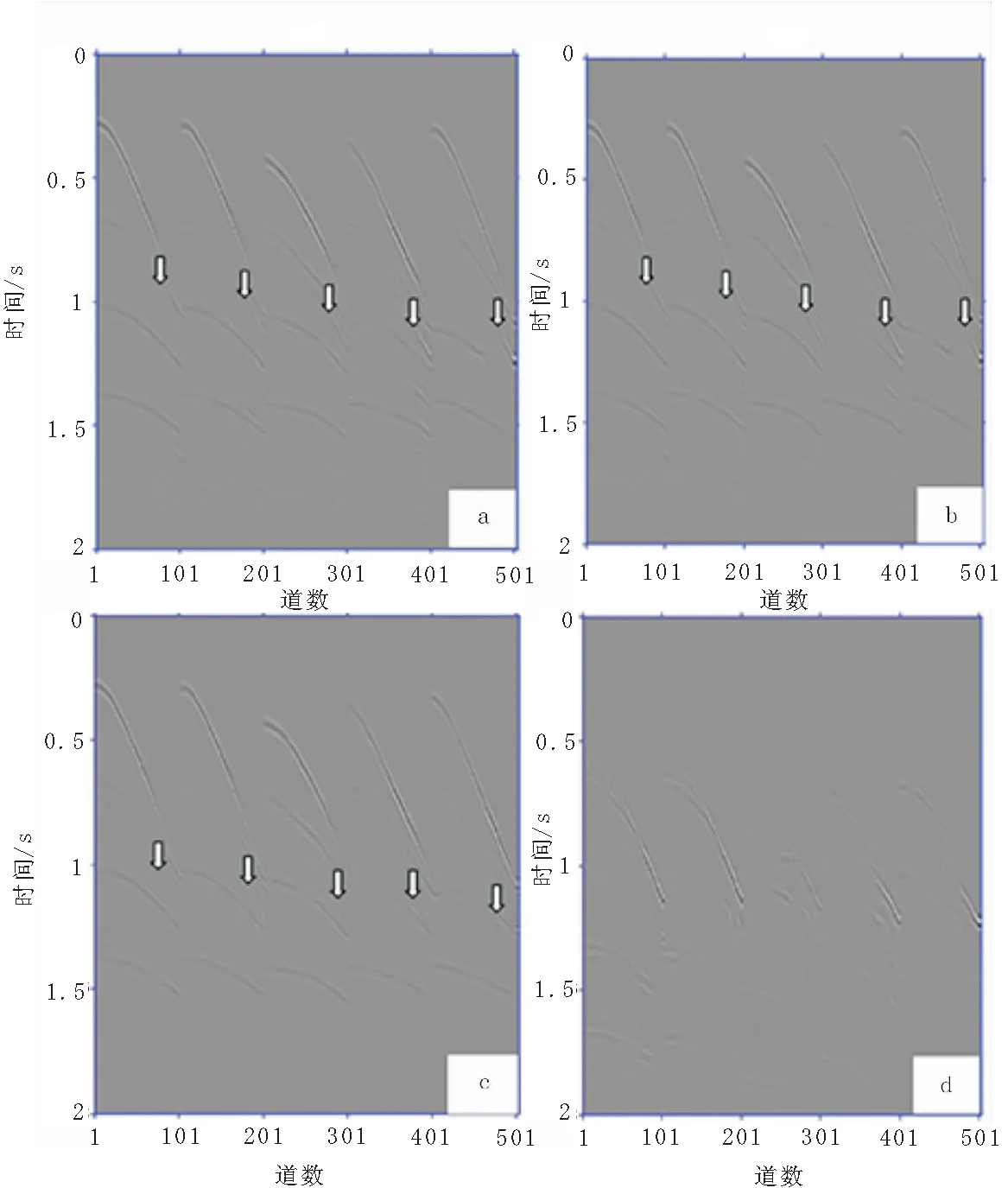
图3 模型一压制多次波前后炮集数据对比图Fig．3 Results of shot gather data by various multiple elimination method of model 1(a)原始五炮记录；(b)L2范数自适应减结果；(c)L1范数自适应减结果；(d) L1范数自适应减方法减掉的多次波

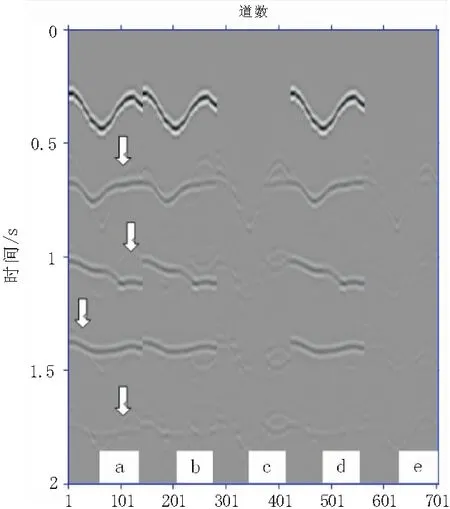
图4 模型一压制多次波前后零炮检距 剖面对比图Fig．4 Results of zero offset section of model 1 by various multiple elimination method(a) 原始含多次波零炮检距记录；(b) L2范数自适应减结果；(c) L2范数自适应减方法减掉的多次波； (d)L1范数自适应减结果；(e) L1范数自适应减方法减掉的多次波

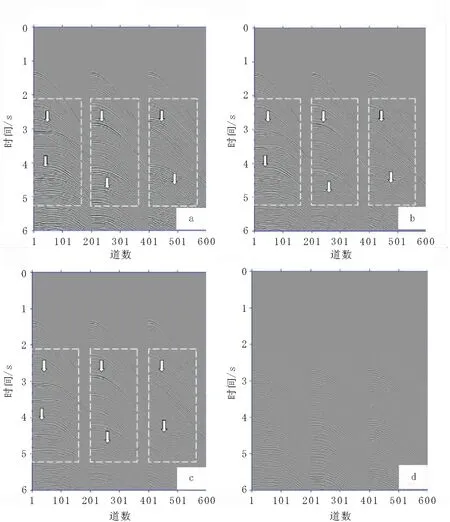
图5 模型二压制多次波前后炮集数据对比图Fig．5 Results of shot gather data by various multiple elimination method of model 2(a)原始三炮记录；(b)L2范数自适应减结果；(c)L1范数自适应减结果；(d)L1范数自适应减方法减掉的多次波

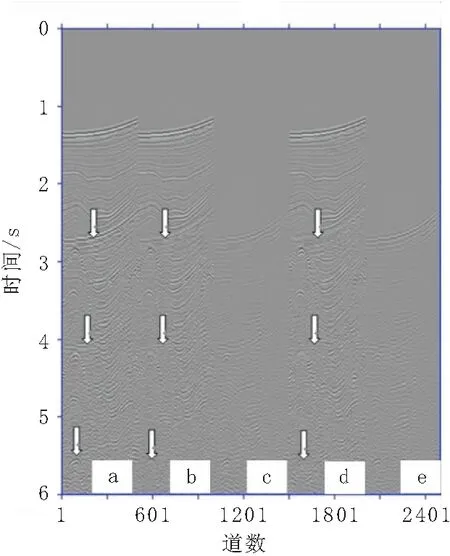
图6 模型二压制多次波前后零炮检 距剖面对比图Fig．6 Results of zero offset section of model 2 by various multiple elimination method(a)原始含多次波的零炮检距记录；(b)L2范数自适应减结果；(c)L2范数自适应减方法减掉的多次波； (d)L1范数自适应减结果；(e) L1范数自适应减方法减掉的多次波

3 结论

应用基于IRLS算法的混合L1/L2范数方法，将L1范数多次波自适应减方法具体实现，并进行了模型数据与实际地震数据的处理，实现了自由表面相关多次波的迭代自适应减。结果表明，文中方法对于复杂情况下的多次波压制也具有较好的适应性。通过对理论模型数据和实际数据多次波压制效果对比可知，基于L1范数自适应减方法能较好地匹配预测多次波模型和地震记录中的实际多次波，从而能更好地压制多次波，并保护有效波的能量。但同时，该方法的计算量比L2范数自适应减方法相比要大，计算过程也较L2范数自适应减方法复杂，但该方法把L1范数与L2范数自适应减方法很好地结合起来，适应性较强，且共轭梯度法具有收敛速度快的特点，综合考虑之下认为该方法可以被接受。在实际应用中为获得更好的压制效果，应注意以下方面：

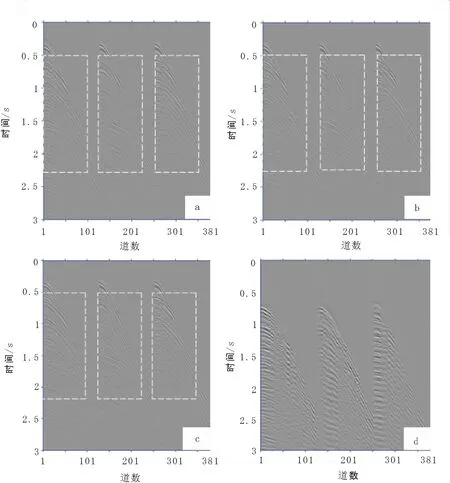
图7 实际数据压制多次波前后炮集数据对比图Fig．7 Results of shot gather data by various multiple elimination method of real data(a)原始三炮含多次波炮集；(b)L2范数自适应减结果；(c)L1范数自适应减结果；(d)L1范数自适应减方法减掉的多次波

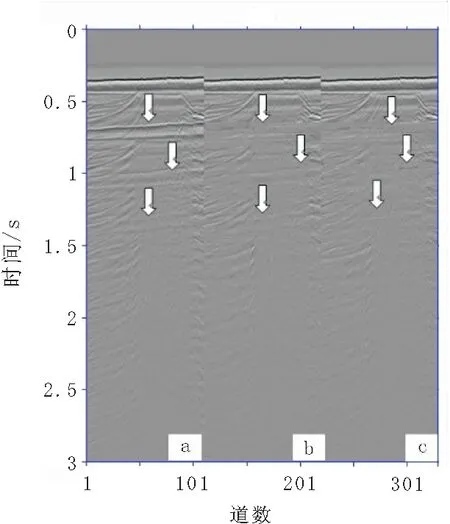
图8 实际数据压制多次波前后零炮检 距剖面图Fig．8 Results of zero offset section of real data by various multiple elimination method(a)原始含多次波的零炮检距记录；(b)L2范数自适应减结果；(c)L1范数自适应减结果

(1)预测多次波模型精度。基于SRME方法原理，由反馈迭代法得到预测的多次波模型。如果预测的多次波模型误差较大，将会影响多次波的压制效果或者导致有效波受损。通常在测线两端，由于预测多次波的数据信息有限，容易导致预测多次波不准确，从而影响多次波的压制效果。

(2)滤波算子长度。滤波算子s的长度不宜过大(一般不超过35个采样点)，否则可能会导致有效波受损；但也不能过小(一般不小于8个采样点)，否则可能会导致匹配不足而有较大的多次波剩余，其一般在10到30个采样点之间取值。

(3)时窗长度及其控制。对各道地震记录分时窗处理，考虑了多次波关于时间上的变化，可使多次波压制效果更好。关于时窗长度的选择不是越短越好(例如一个阶次的多次波分多个时窗处理)，否则会导致有效波受损严重；时窗长度也不宜取得过长(例如一个时窗内处理多个阶次的多次波)，否则会导致多次波去除不干净，一般是在一个时窗内处理一个阶次的多次波。

参考文献：

[1] VERSCHUUR D J. 地震多次波去除技术的过去现在和未来[M]. 陈浩林，张保庆，刘军,等,译,北京：石油工业出版社，2010.

[2] VERSCHUUR D J. Surface-related multiple elimination: an inversion approach: Ph.D.thesis[M]. Delft: University of Technology, 1991.

[3] VERSCHUUR D J, BERKHOUT A J, WAPENAAR C P A. Adaptive surface-related multiple elimination [J]. Geophysics, 1992, 57(9):1166-1177.

[4] VERSCHUUR D J, BERKHOUT A J. Estimation of multiple scattering by iterative inversion ,partⅠ:theoretical considerations[J].Geophysics,1997,62(5):1586-1595.

[5] CLAERBOUT J F, MUIT F. Robust modeling with erratic data[J]. Geophysics,1973,38: 820-844.

[6] BUDE K P, LANGAN R T. Hybrid l1/l2 minimization with applications to tomography[J].Geophysics,1997,62:1183-1195.

[7] GUITTON A , VERSCHUUR D. J. Adaptive subtraction of multiples using the L1-norm[J]. Geophysical Prospecting, 2004, 52: 27-38.

[8] GUITTOH A .Implementation of a nonlinear solver for minimizing the Huber norm[J].SEP,2000,103:281-289.

[9] Antoine Guitton. Huber solver versus IRLS algorithm for quasi L1inversion[J]. Stanford Exploration Project, Report 103, April 27, 2000, 103:205-266.

[10] ADAM GERSZTENKOR, BEE BEDNAR J, LARRY LINES R. Robust iterative inversion for the one-dimensional acoustic wave equation[J]. Geophysics, 1986,51(2):357-368.

[11] DARCHE G. Iterative L1 deconvolution[J]. SEP Annual Report , 1989,61: 281-301.

[12] WEGLEIN A B. Multiple attenuation: an overview of recent advances and the road ahead[J].The Leading Edge, 1999, 18(1): 40- 44.

[13] 李学聪，刘伊克，常旭，等. 均衡多道1范数匹配多次波衰减的方法与应用研究[J]. 地球物理学报，2010，53(4)：963-973.

[14] 刘光. 压制自由表面相关多次波的自适应减方法研究及应用[D]. 北京: 中国地质大学，2009.

[15] 黄新武，牛滨华，刘光,等. 基于数据一致性原理预测与压制自由表面多次波的效果分析[J]. 石油地球物理勘探，2009， 44 (4)：409- 416.

[16] 牛滨华，沈操，黄新武. 波动方程多次波压制技术的进展[J]. 地球物理学进展，2002，17 (3) ：480- 485.