垂直及倾斜接触面电测深曲线特征
汤井田, 谭 洁, 潘克家
(中南大学 地球科学与信息物理学院, 长沙 410083)
0 引言
直流电阻率法是以地壳中岩石和矿石的导电性差异为物理基础,通过观测与研究人工建立的地中稳定电流场的分布规律,进行找矿和解决地质问题的一组电法勘探分支方法,无论在普查金属、非金属矿产和研究地质构造方面,还是在水文、工程、环境地质调查以及勘查能源等方面,均取得了良好的地质效果,发挥着重要作用。
卡连诺夫[1]早在上世纪三十年代提出,当地下存在倾斜接触面时,研究点源电流场的分布具有重要的理论与实践意义。此后R.F.Aldredge[2], ,B.H.达连诺夫[3]等人也对该问题进行了研究,K.Maeda[4]利用点源多次镜像进行求解,但仅适用于π是α的整数倍,或者(ρ2-ρ1)/(ρ2+ρ1)=-1(如ρ2=0)且π/2是α的整数倍,不及解析法的应用广泛。
作者详细推导了倾斜接触面存在时电测深视电阻率的实用计算公式[5-11,14],对进一步研究提供了一定的基础,分析了对称四极测深装置[12-13]下不同的布极方位时的测深视电阻率曲线特征,对实际工作仍有一定的指导作用。
1 公式推导
利用解析法求解倾斜接触面存在时的电位,是通过边界条件求解与实际问题相应的拉普拉斯方程。
图1为点源场中倾斜接触面模型结构示意图,A为点源,M为测点。采用柱坐标系,以斜面与地表的交线为Z轴,于是A点的柱坐标为(r0,0,0)。设任意一点M的柱坐标为(r,θ,z),当0<θ<α时,M位于二面角α内;当α<θ<π时,M位于二面角α外。

图1 点源场中斜接触面模型结构示意图Fig.1 Field of a point source situated on the earth above a dipping bed
问题在于求大地任一点M(r,θ,z)处的电位
U(r,θ,z):
显然电位满足拉普拉斯方程:
(1)
U1、U2满足以下边界条件:
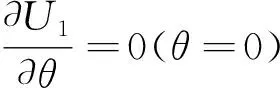
(2)U1=U2(θ=α)。
令U(r,θ,z)=P(θ)Q(r,z),用分离变量法求解该定解问题可以得到:

(2)

(3)
为了便于编程计算,将解化为级数形式。
(1)当r>r0,且Res>-1/2时,交换积分次序,可改写成式(4)。
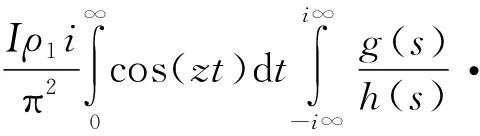
Is(r0t)Ks(rt)ds
(4)
式中
g(s)=cos[s(π-θ)]+kcos[s(a-θ)];h(s)=sin(sπ)+ksin(sa)。
(2)当r
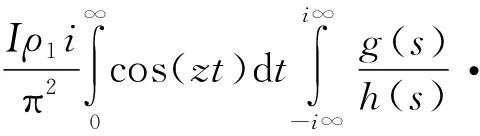
Is(rt)Ks(r0t)ds
(5)
U2的改写同理可得。
设F(s)表示上面两式中内层积分的被积函数。为了应用留数定理来计算积分,先考虑F(s)的奇点。由于g(s)与第一、第二类Bessel函数Is、Ks是s的解析函数,故F(s)的奇点就是h(s)的零点,即方程h(s)=0的根,该方程sin(sπ)+ksin(sa)=0(式中a=2α-π)依具体的k值及s的值而定。
数学上可以证明,在0<α<π的情况下,方程的根必为实数,故方程写为h(x)=0。且|k|<1的情形下,h(x)=0的根必为单根。此时h(x)=sin(xπ)+ksin(xa)=0的根x满足sin2(xπ)=k2sin2(xa)。
当0<|x|<1/2时,因0≤|α|<π,故0≤|xα|<|x|π<1/2。又在0≤φ<π/2时,(sinφ)′=cosφ>0,故sinφ是递增函数。
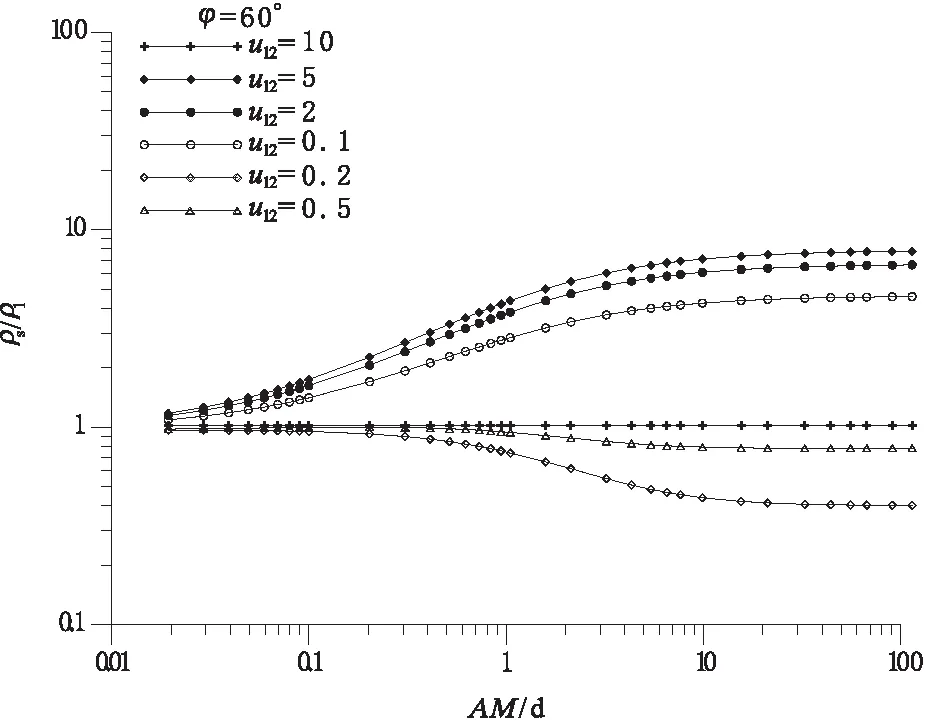
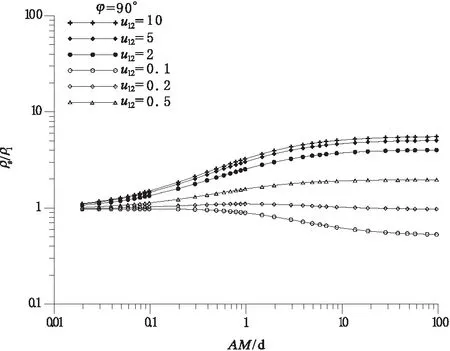
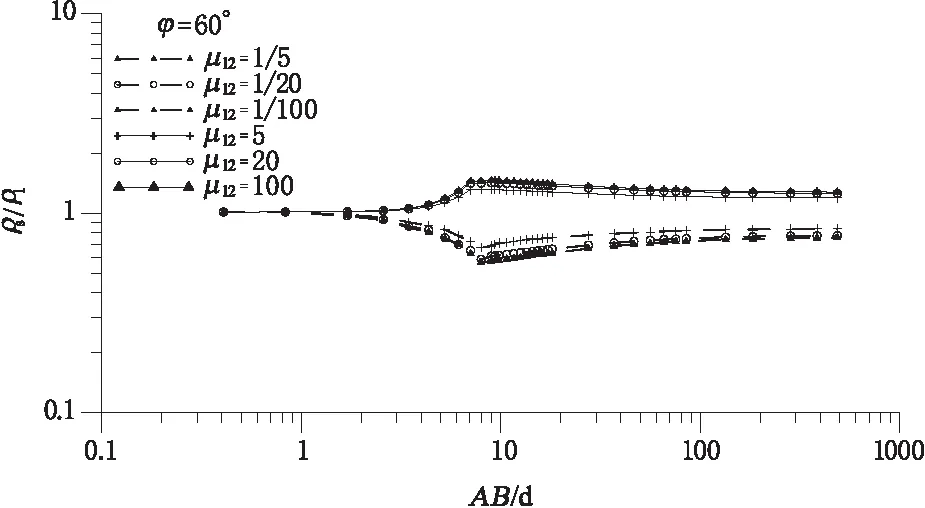
于是sin|xα| 由此可见,在以原点为中心、以δ(<1/2)为半径的圆内,仅有s=0是方程的单根,从而原点是F(s)的单极点,故从iδ到-iδ沿这圆的左半部分c积分: (6) (7) 同样, (8) 于是 (9) 设|k|<1的情形,将[-iym,iδ]与[iδ,iym]二线段以及半圆c与折线Lm接成的围线记为Cm,据留数定理,依正向积分: (10) 式中N是在Cm内h(x)=0的正根xi的个数,而 (11) 故: (12) 令m→∞(从而ym→∞,N→∞)得到Cauchy主值: (13) 将求和下标j改写成m,可得: (1)当r>r0时, (14) (2)当r (15) 代入式(2)与式(3)得到: (1)当r>r0时, (16) (2)当r 由于 (17) 则 (18) (19) 方程h(x)=0的单根xm就是F(s)的单极点,也就是g(s)/h(s)及cos[s(π-θ)]/h(s)的单极点,在这些点处: (20) (21) 由此可见,当|k|<1时,计算公式为: (22) (23) 式中a=2α-π。 在公式推导的基础上,绘制了二极装置下点源场中倾斜接触面电测深曲线[19-21],对垂直接触面上不同布极方位电测深曲线特征进行了详细讨论。 图2为二极测深装置的模型结构示意图。模型参数:装置轴与接触面垂直,倾斜接触面的角度分别取为30°、45°、60°以及90°,测点M横坐标设为d,取为10 m,源点A横坐标分别取10.2 m、10.3 m、10.4 m、10.5 m、10.6 m、10.7 m、10.8 m、10.9 m、11.0 m、12.0 m、13.0 m、14.0 m、15.0 m、16.0 m、17.0 m、18.0 m、19.0 m、20.0 m、25.0 m、30.0 m、40.0 m、50.0 m、60.0 m、70.0 m、80.0 m、100.0 m、150.0 m、200.0 m、300.0 m、400.0 m、500.0 m、600.0 m、800.0 m、1 000.0 m。 图2 二极测深装置模型结构示意图Fig.2 The sketch of geoelectricity model with pole-pole array 二极装置下,视电阻率定义为: 视电阻率曲线见图3-图6。 图3 倾斜角度φ为30°,μ12分别取10、5、2、0.5、0.2、0.1Fig.3 Apparent resistivity curves for a dipping angle of 30° at constant values of μ12 as would be obtained by pole-pole array, where search electrodes are laid out in the down-dip direction 图4 倾斜角度φ为45°,μ12分别取10、5、2、0.5、0.2、0.1Fig.4 Same as Fig.3 but for a dipping angle of 45° 图5 倾斜角度φ为60°,μ12分别取10、5、2、0.5、0.2、0.1Fig.5 Same as Fig.3 but for a dipping angle of 60° 图6 倾斜角度φ为90°,μ12分别取为10、5、2、0.5、0.2、0.1Fig.6 Same as but for a dipping angle of 90° 当点源跨过接触面时,测点M横坐标为10 m,源点A横坐标为9.5 m、9.4 m、9.3 m、9.2 m、9.1 m、9.0 m、8.0 m、7.0 m、6.0 m、5.0 m、4.0 m、3.0 m、2.5 m、2.0 m、1.5 m、1.0 m、0.5 m、-0.5 m、-1.0 m、-2.0 m、-3.0 m、-4.0 m、-5.0 m、-6.0 m、-7.0 m、-8.0 m、-9.0 m、-10.0 m、-11.0 m、-12.0 m、-15.0 m、-20.0 m、-30.0 m、-50.0 m、-100.0 m、-200.0 m、-500.0 m,相应的曲线见图7-图10。 图7 倾斜角度φ为30°,μ12分别取10、5、2、0.5、0.2、0.1Fig.7 Apparent resistivity curves for a dipping angle of 30° at constant values of μ12 as would be obtained by pole-pole array, where search electrodes are laid out perpendicular to the strike 图8 倾斜角度φ为45°,μ12分别取为10、5、2、0.5、0.2、0.1Fig.8 Same as Fig.7 but for a dipping angle of 45° 图9 倾斜角度φ为60°,μ12分别取10、5、2、0.5、0.2、0.1Fig.9 Same as Fig.7 but for a dipping angle of 60° 图10 倾斜角度φ为90°,μ12分别取10、5、2、0.5、0.2、0.1Fig.10 Same as Fig.7 but for a dipping angle of 90° 由图3-图10可以看出,测深轴跨过接触面时,在接触面附近视电阻率曲线突变,而未跨过接触面的曲线变化平缓,对比两组曲线,可确定接触面的位置;同时,接触面两侧介质的电阻率相差越大,接触面对视电阻率曲线的影响也越大。 本节重点讨论了对称四极装置下垂直接触面存在时的电测深曲线(图11、图12),通过求解不同模型下的视电阻率,得到对称四极装置下视电阻率曲线随各个参数的变化规律。 图11为对称四极测深装置的模型示意图,对称四级装置下视电阻率定义为: 图11 对称四极测深装置模型结构示意图Fig.11 The sketch of geoelectricity model with schlumberger array 图12 对称四极测深装置在垂直接触面上布极示意图Fig.12 The sketch of geoelectricity model with schlumberger array over a vertical sheet 图12的模型参数:垂直接触面两侧电阻率之比ρ2/ρ1分别取为0.01、0.05、0.5、5、50、100;装置轴与接触面所成的角度分别取为30°、45°、60°以及90°,测点与接触面的距离设为d,取为10 m。视电阻率曲见图13-图17。 图13 φ=0°时视电阻率曲线,μ12分别取0.01、0.05、0.5、5、50、100Fig.13 Apparent resistivity curves for a intersection angle of 0° at constant values of μ12 as would be obtained by schlumberger array, where search electrodes are laid out perpendicular to the strike 图14 φ=30°时视电阻率曲线,μ12分别取0.01、0.05、0.5、5、50、100Fig.14 Same as Fig.13 but for a intersection angle of 30° 图15 φ=45°时视电阻率曲线,μ12分别取0.01、0.05、0.5、5、50、100Fig.15 Same as Fig.13 but for a intersection angle of 45° 图16 φ=60°时视电阻率曲线,μ12分别取0.01、0.05、0.5、5、50、100Fig.16 Same as Fig.13 but for a intersection angle of 60° 图17 φ=90°时视电阻率曲线,μ12分别取0.01、0.05、0.5、5、50、100Fig.17 Same as Fig.13 but for a intersection angle of 90° 从图13-图17可以看出,对称四极装置在垂直接触面上的测深曲线,总体呈现先增大后趋于定值的趋势。φ=0°即装置轴AMNB平行接触面时,曲线的左侧渐近值为ρ1,右侧渐近值为ρs=2ρ1ρ2/(ρ2+ρ1),在AB/d>>20时,界面对测深视电阻率的影响已可忽略;垂直接触面时,曲线在AB/d=2处畸变达到极大值,垂直界面位置对应于ρs极大(当ρ2/ρ1>1)或极小(ρ2/ρ1<1);当ρ2/ρ1→∞时,ρs极大值等于1.45ρ1;当ρ2/ρ1=0时,ρs极大值等于0.55ρ1;右支渐近线ρs→ρ1,与ρ2/ρ1值无关;当布极方位与处置接触面走向为不同夹角时,测深曲线形状将介于上述两种情况之间。 在同一垂直接触面上,对比对称四极装置的装置轴平行接触面走向和垂直接触面走向时的测深视电阻率曲线可见,因垂直接触面的存在,给测深曲线带来了一定的畸变,给实际异常曲线的解释带来了干扰。因此对其电测深理论正演曲线的研究,有助于对实测电测深曲线的分析认识和推断解释。显然,垂直接触面走向布极时,测深曲线的畸变比平行接触面走向布极时复杂,在这种情形下,实际勘探中一般要求平行构造走向布极。 界面附加进行十字测深,由两个方向ρs曲线的差异可以肯定垂直分界面的存在,而且可以大致确定其位置。 通过作者对视电阻率曲线的分析及误差对比可得到如下结论: (1)平行接触面时,曲线的左侧渐近值为ρ1,右侧渐近值为ρ∞=2ρ1ρ2/(ρ2+ρ1);垂直接触面时,曲线在AB/d=2处畸变达到极大值,垂直界面位置对应于ρs极大(ρ2/ρ1>1)或极小(ρ2/ρ1<1);当ρ2/ρ1=∞时,ρs极大值等于1.45ρ1;当ρ2/ρ1=0时,ρs极大值等于0.55ρ1,右支渐近线ρ∞→ρ1,与ρ2/ρ1值无关。 (2)当布极方位与处置接触面走向为不同夹角时,测深曲线形状将介于上述两种情况之间。 (3) 界面附加进行十字测深,由两个方向ρs曲线的差异可以肯定垂直分界面的存在,而且可以大致确定其位置。 (4)实际勘探中一般要求平行构造走向布极。 参考文献: [1] 卡连诺夫.E.H.垂向电测深曲线解释[M].北京:石油出版社,1959. [2] ALDREDGE R F .The Effect of Dipping Strata on Earth Resistivity Determination[J].Colorado School of Mines Quart,1937,32(1):169-186. [3] B.H.达连诺夫.石油与天然气电法勘探[M]. 林振民,译,北京:地质出版社,1953. [4] MAEDA K . Apparent resistivity curves for dipping bnd[J] .Geophysics,1955,120(1):123-139. [5] 史磷华.三层倾斜层的K型地电断面直流电测深的正反演问题[J].矿产及地质,1990,15( 4):63-68. [6] 葛为中,阮百尧.直立多层介质地面点源电场的递推公式[J].桂林冶金地质学院报,1990,10(2):173-181. [7] 陈福萍,于安良.直立接触面视电阻率量板[J].地质与勘探,1978(7):73-78. [8] 刘象勤,李纯志.直立岩层ρsηs测深理论曲线正演及程序[J].物探化探计算技术,1990, 12(2):159-167. [9] 刘象勤,李纯志.二维直立岩层电阻率测深异常曲线的某些特征[J].矿产及地质,1992(3):207-212. [10] 屈超群.二度体地形对点源场影响的数学分析[J].应用数学学报,1977(2):48-54. [11] 屈超群,张静.点源场计算方法[M].昆明:云南科学技术出版社,1999. [12] 李金铭.地电场与电法勘探[M].北京:地质出版社,2005. [13] 傅良魁.电法勘探教程[M].北京:地质出版社,1983. [14] 王磊. 点电源场中垂直接触带地表节点电位求解分析[J].电脑开发与应用,2008,21(3):50-52. [15] 张秋光. 场论(中册)[M]. 北京:地质出版社,1985. [16] 王元明. 数学物理方程及特殊函数[M]. 北京:高等教育出版社,2004. [17] 任怀宗,师先进.特殊函数概论[M].长沙:中南工业大学出版社,1986. [18] 李寿贵,尹水仿.复变函数与积分变换[M].北京:科学出版社,2009. [19] 刘卫国,易刚.C++程序设计实践教程[M].北京:中国铁道出版社,2008. [20] IVOR HORTON. Visual C++2008入门经典[M].北京:清华大学出版社,2009. [21] 罗延中 张桂青.电子计算机在电法勘探中的应用[M].武汉:武汉地质学院出版社,1987.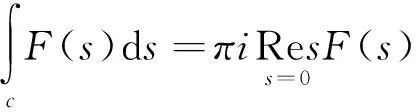

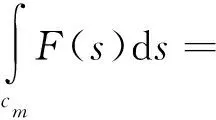




2 不同装置下倾斜接触面电测深曲线
2.1 二极装置下倾斜接触面电测深曲线








2.2 不同布极方位下垂直接触面的电测深曲线
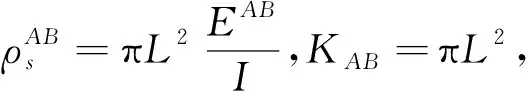






3 结论

