关于破解连接体问题的三个“杀手锏”

李玲丽

(四川省米易中学校 四川 攀枝花 617200)

连接体问题在高中物理中占有非常重要的地位，综合性强，题型灵活多变，考查考生综合分析能力、推理能力．近几年高考对能力的要求不断提高，加强了对非平衡状态下连接体问题的考查力度．然而大部分考生面对连接体问题时，往往看着就产生畏惧感，无法找准切入点，更无法把相关的物理量有机地联系起来，从而导致连接体问题失分惨重．笔者根据亲身的教学经历，总结了破解连接体问题的三个“杀手锏”，引导2013届考生掌握并加以灵活应用，结果在今年高考中，考生对连接体问题的解答出现了较大改观，考生能抓住其本质，命中其要害，得分率明显提高．

1 巧选研究对象(系统) 熟练应用整体法和隔离法

高中物理中把两个或两个以上相互连接参与运动的物体称为连接体．在分析连接体问题时，巧选研究对象，可起到事半功倍的效果．应用整体法是把整个系统作为研究对象，对其进行受力分析时，不必考虑物体之间的“内力”，只考虑整个系统之外的力．应用隔离法是把系统中的各个部分(或某一部分)隔离，作为单独的研究对象来分析的方法，此时系统的“内力”就成为该研究对象的“外力”，在进行受力分析时应引起重视．而大部分连接体问题要将整体法和隔离法结合使用，所以，考生必须树立强烈的对象意识.现笔者就举例加以说明．

【例1】如图1，在倾角为30°的光滑斜面上放置质量分别为m和2m的4个木块，其中上面两个木块用一不可伸长的轻绳相连，木块间的最大静摩擦力是fm，现用平行于斜面的拉力F拉其中一个质量为2m的木块，使4个木块以同一加速度沿斜面向下运动，则拉力F的最大值是

A．0.6fmB．0.75fm

C．1.5fmD．fm

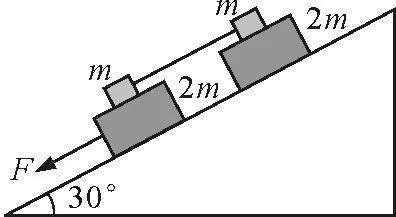
图1

解析:在分析时，巧选研究对象是非常关键的．

示例中考生擅长以4个木块作整体分析

F+ 6mgsin30°= 6ma

但在采用隔离法时，多数考生确定上面m和2m为研究对象，或者直接是其中一个m，多了绳上的拉力，导致未知数偏多，方程过于烦琐．若选择两个m和上面2m为系统，绳上的拉力就成为系统的“内力”，情况就变简单了：fm+ 4mgsin30°=4ma，联立求解，知选项C正确．

2 通过轻绳 轻弹簧相连接的物体或物体系统 拉力 加速度大小通常相等

在连接体问题中，要把各个物体联系起来，弹力、加速度是破解连接体问题的“桥梁”．

图2

【例2】如图2，一根不可伸长的轻绳两端分别系着小球A和物块B，跨过固定于斜面顶端的滑轮O，倾角为30°的斜面置于水平地面上．A的质量为m，B的质量为4m．起初，用手托住A，使OA段绳恰处于水平伸直状态(绳上无拉力)，OB绳平行于斜面，此时B静止不动．将A由静止释放，在下摆过程中，斜面始终保持静止，下列判断正确的是

A．物块B受到的摩擦力先减小后增大

B．地面对斜面的摩擦力方向一直向右

C．小球A的机械能不守恒

D．小球A的机械能不守恒，A和B系统的机械能守恒

解析:考生普遍选D，光凭感觉、惯性思维确定了答案，导致痛失6分．

首先，以斜面和B为系统，绳OA上拉力的水平分力始终向左，故选项B正确．

其次，隔离A，B，找准联系它们的桥梁：绳上拉力始终大小相等．分析B：Ff=4mgsin30°沿斜面向上(起初B静止不动)．判断在A下摆过程中，B始终不动：当A下摆至最低点时绳上拉力最大(假设B不动)．A下摆过程

在最低点

可知FT=3mg，此时B上拉力也是最大的，得Ff=mg沿斜面向下，故B不动，则小球A全程机械能守恒，选项C和D错误．物块B受到的摩擦力，先减小至零，再反向增大，故选项A正确．

3 准确建立物体系统内的功能关系 判断连接体间是直接存在速度相等关系 还是应该间接地把速度作必要的分解

在备战高考期间，高三学子遇到连接体的习题可以说多如牛毛．但能真正掌握的考生并不多．问题表现在：要么看着连接体就习惯性地认为它们速度相等；要么表达系统功能关系时，研究对象出现错误；要么不能有效地切入过程．现就一道诊断性考题加以说明．

【例3】如图3，在竖直平面内有轨道ABCDE，其中BC是半径为R的四分之一圆弧，AB(AB>2R)是竖直轨道，CE是水平轨道，CD>2R．AB与BC相切于B点，BC与CE相切于C点，轨道的AD段光滑，DE段粗糙且足够长．一根长为2R的轻杆两端分别固定着质量均为m的相同小球P，Q(视为质点)，将轻杆锁定在图示位置，并使Q与B等高．现解除锁定释放轻杆，轻杆将沿轨道下滑，重力加速度为g．

(1)Q球经过D点后，继续滑行距离s停下(s>2R)．求小球与DE段间的动摩擦因数．

(2)求Q球到达C点时的速度大小．

图3

解析:(1)如图4分析小球滑行的过程，由能量守恒得

mgR+3mgR=μmgs+μmg(s-2R)

解得

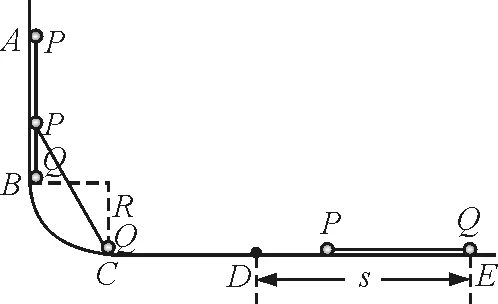
图4

(2)轻杆释放到Q球到达C点时，系统的机械能守恒，设P，Q两球的速度大小分别为vP，vQ，则

mgR+mg(3R-2Rcos30°)=

又

vPcos30°=vQcos60°

联立解得

当时全市超过50%的考生认为两球速度相等，忽略了速度的方向，当然也就没有把速度做必要的分解；再就是对滑行过程分析不透彻，不能根据力和运动的关系正确分析出两球的运动过程，无法准确表达系统中各个力所做的功，导致能量方程无效．

在各种考试中，虽然连接体问题已成为命题者青睐的对象，但通过以上思考，以及实例分析，我们可看出连接体问题也不是想象中的那么困难．总之，不论它的综合性有多强，题型多么灵活多变，只要我们找准关键，就能巧妙地破解连接体问题．