人工鱼群算法在单轴旋转惯导系统轴向陀螺漂移辨识中的应用
雷 雯
引言
激光陀螺具有结构简单、体积小、质量轻、精度高等优点,成为捷联惯导系统的理想器件,已大量成功地运用于航空、航天、航海以及地面定位与定向等领域[1-3]。近几年,以光学陀螺为惯性元件的旋转式惯性导航系统已经成为研究热点,并有取代传统机械陀螺的趋势[4-6]。从原理上讲,单轴旋转可以消除垂直于旋转轴方向上的惯性器件误差,但不能消除旋转轴上的惯性器件误差,特别是轴向陀螺漂移,因此单轴旋转惯导系统的精度主要由轴向陀螺漂移决定。文献[7]提出了一种基于姿态解算的轴向陀螺漂移的估计方法,单轴旋转惯导系统的定位精度达到1nm/24h,文献[8]将最小二乘支持向量机用于单轴旋转惯导系统轴向陀螺漂移辨识,并利用混沌粒子群算法对其参数进行优化以提高辨识精度,定位精度达到1nm/72h。人工鱼群算法AFSA(artificial fish swarm algorithm)是受鱼群行为的启发,由李晓磊于2002年提出的一种基于动物行为的群体智能优化算法,是行为主义人工智能的一个典型应用[9]。这种算法源于鱼群的觅食行为,在一片水域中,鱼往往能自行或尾随其他鱼,找到营养物质多的地方,因而鱼生存数目最多的地方一般就是本水域中营养物质最多的地方。人工鱼群算法根据这一特点,通过构造人工鱼来模仿鱼群的觅食、聚群、追尾及随机行为,从而实现寻优。人工鱼群算法可以克服传统优化方法的许多不足和缺陷,实现和操作简单。对函数不连续、不可微、局部极值点密集等苛刻的情况,更加具有很好的寻优能力。针对ASFA的不足,对ASFA中固定视野,固定步长问题进行了改进,以提高收敛速度和参数估计精度。本文首次利用人工鱼群算法对单轴旋转惯性导航系统轴向陀螺漂移进行辨识,提高惯性导航系统的导航精度。
1 ASFA基本原理
ASFA是一种群集智能优化算法,它采用了自上而下的寻优模式模仿自然界鱼群觅食行为,主要利用鱼的觅食、聚群和追尾行为,构造了个体的底层行为,通过鱼群中个体的局部寻优,达到全局最优值在群体中突现出来的目的[10]。其算法相关定义及具体描述如下:
人工鱼群个体的状态可表示为向量X=(X1,X2,…,Xn),其中Xi为欲寻优的控制变量,人工鱼当前位置的食物浓度为f(X),人工鱼个体之间的距离表示为dij=Xi-Xj,即向量Xi-Xj的二范数,Visual表示为人工鱼的感知距离,Step表示人工鱼移动步长的最大值,δ表示拥挤度因子,N表示参与寻优的人工鱼数目,即群体规模。
1.1 觅食行为
设置人工鱼当前状态位置,在其感知范围内随机选择一个状态Xi,当该状态食物浓度大于当前状态时(即F(Xj)>F(Xi),此处以求极大值问题为例,求极小值问题可以和此进行互换),则向该方向前进一步;反之,则重新随机选择状态Xj,判断是否满足前进条件;反复一定次数后,如果仍不满足前进条件,则随机移动一步。数学表达式表示为

式中:k=1,2,…n;xjk、xik和xinextk分别为人工鱼状态向量Xj、Xi和人工鱼下一步状态向量Xinext的第k个分量;Rand()为(0,1)间的一个随机数。
1.2 聚群行为
人工鱼当前状态为Xi,探索在其感知范围内(dij<Visual)伙伴的数目nf,形成集合 Ni,若nf≥1,即Ni不为空集,表明在其感知范围内有其他伙伴存在,计算这些伙伴的中心位置Xc:

式中:xck为中心位置状态向量Xc的第k个分量;Xjk为当前感知范围内的第j个伙伴Xj第k个分量。中心位置的食物浓度为F(Xc),如果F(Xc)/nf>δ,表明伙伴中心位置有较多的食物且不太拥挤,则朝伙伴中心位置方向前进一步,即按(3)式执行:
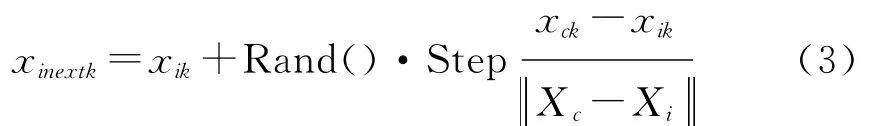
否则,人工鱼执行觅食行为。
若nf=0,表明可见域内不存在其他伙伴,也执行觅食行为。
1.3 追尾行为
人工鱼当前状态为Xi,探索在其感知范围内(dij<Visual)伙伴的数目nf,且伙伴中F(Xj)为最大的伙伴Xmax,如果Fmax>δ,表明伙伴Xmax具有高的食物浓度并且周围不太拥挤,则人工鱼群朝伙伴Xmax的方向前进一步,即按(4)式执行:

否则,人工鱼执行觅食行为。
若nf=0,表明可见域内不存在其他伙伴,也执行觅食行为。
设置一个公告板,记录最优的一条人工鱼的状态。根据所要解决的问题性质,对人工鱼当前所处的环境进行评价,从而选择一种行为。算法的终止条件一般有两种:一是判断是否达到预设的精度指标;二是判断某一区域人工鱼数目所占的比率。
2 模型建立
对于舰船应用的高精度惯性导航系统而言,可以延长对准时间以提高导航精度,故一般选用16h或更长时间。由于轴向陀螺漂移的可观测性很差,可以利用系统位置信息和整个环境温度变化情况来精确估计轴向陀螺漂移。具体方法如下:利用4h来实现精确的水平对准,然后转入导航,利用12h内的导航经纬度信息和温度信息作为观测量输入到ASFA中,采用离线仿真方法,确定使得72h内定位误差最小的漂移值为轴向陀螺漂移的真值,利用12h内的导航经纬度信息和温度信息作为模型的输入,以轴向陀螺漂移的真值为输出建立模型,从而获得最优的ASFA参数,利用最优参数来对轴向陀螺漂移进行精确辨识,扣除掉轴向陀螺漂移后系统再次转入导航状态,进行导航解算。
该试验采用激光陀螺单轴旋转惯导系统中2个水平陀螺零偏稳定性优于0.003°/h,轴向陀螺零偏稳定性优于0.002°/h,加速度计零偏稳定性优于20μg。以系统22组实验中初始对准过程中实测的纬度误差和温度变化量为研究对象,系统初始纬度为28.222°,具体如表1所示。将3组没有参加建模的实验数据作为检验样本以考察其辨识能力。表2给出了利用ASFA辨识前后的导航精度,图1给出了第一组检验样本利用ASFA建模后的定位误差曲线,可以看出,辨识后系统导航误差优于0.5nm/72h,说明轴向陀螺漂移辨识误差优于0.000 3°/h,辨识后系统的定位精度大大提高。

表1 轴向陀螺漂移辨识模型样本Table 1 Sample data of axial RLG drift

表2 利用ASFA对轴向陀螺漂移的辨识结果Table 2 Identification result of axial RLG drift by ASFA
为了进一步验证ASFA辨识轴向陀螺漂移方法的有效性,利用激光陀螺单轴旋转惯导系统进行了车载试验。将惯导系统放置在试验车上,启动系统完成初始对准,在16h的对准时间内完成轴向陀螺漂移精确辨识后进行车载试验,其中表2中第一组样本的跑车试验路线图和定位误差曲线如图1所示。
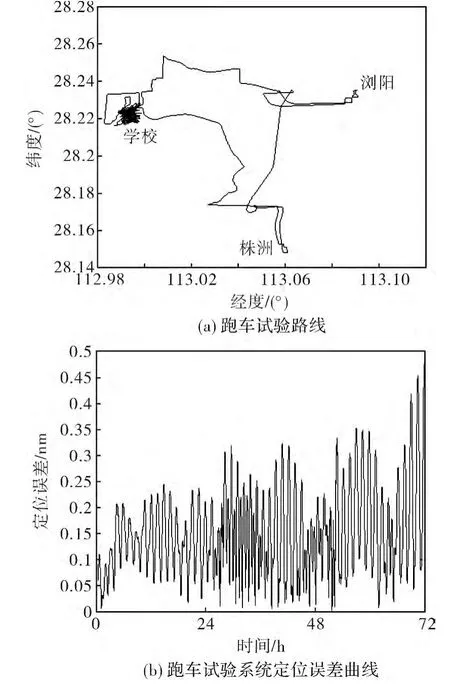
图1 单轴旋转惯导系统跑车试验Fig.1 Vehicle experiment of single-axis rotation inertial navigation system
从表2和跑车试验的结果可以看出,采用ASFA模型对轴向陀螺漂移进行精确辨识后,最大定位误差优于1nm/72h,很好地消除了轴向陀螺漂移对单轴旋转惯导系统的影响,极大地提高了系统的定位精度。
3 结论
采用单轴旋转的惯导系统水平方向上的陀螺漂移可以得到自动补偿,轴向陀螺漂移却只能依靠自身的精度来保证。本文利用ASFA建立了轴向陀螺漂移的精确辨识模型,很好地抑制了轴向陀螺漂移对单轴旋转惯导系统的影响,轴向陀螺漂移辨识精度优于0.0004°/h,提高了导航精度,具有很好的工程实用价值。
[1] Titterton D H,Weston J L.Strapdown inertial navigation technology[M].2nded.United Kingdom:In-stitution of Electrical Engineers,2004.
[2] Mohinder S G,Lawerence R W,Angus P A.Global positioning systems,inertial navigation,and integration[M].US:John Wiley &Sons,Inc.,2001.
[3] Yu Xudong,Gao Na,Long Xingwu,et al.High precision single-axial rotation attitude measurement system [J].Journal of Applied Optics,2010,31(5):54-57.
于旭东,高娜,龙兴武,等.高精度单轴旋转姿态测量系统研究[J].应用光学,2010,31(5):54-57.
[4] Levinson E,Majure R.Accuracy enhancement techniques applied to the marine ring laser inertial navigator(MARLIN)[J].Navigation,1987,34(1):64-86.
[5] Tucker T,Levinson E.The AN/WSN-7Bmarine gyrocompass/navigator[C].CA:Anaheim,2000:348-357.
[6] Yu Xudong.Research on some key technologies for single-axis rotation inertial navigation system with mechanically dithered ring laser gyroscope [D].Changsha:National University of Defense Technology,2011.
于旭东.二频机抖激光陀螺单轴旋转惯性导航系统若干关键技术研究[D].长沙:国防科技大学,2011.
[7] Wu Saicheng,Qin Shiqiao,Wang Shengshu,et al.A new method for the estimate of z-direction ring laser gyro drift based on attitude determination [J].Chinese Journal of Lasers,2010,37(5):1209-1212.
吴赛成,秦石乔,王省书等.基于姿态解算的z向激光陀螺零偏估计方法[J].中国激光,2010,37(5):1209-1212.
[8] Yu Xudong,Zhang Pengfei,Xie Yuanping,et al.I-dentification of axial RLG drifts in single-axis inertial navigation system based on CPSO-LSSVM algorithm[J].2013,35(5):40-44.
于旭东,张鹏飞,谢元平,等.基于CPSO-LSSVM的单轴旋转惯导系统轴向陀螺漂移辨识[J].系统工程与电子技术,2013,35(5):40-44.
[9] Li Xiaolei,Shao Zhijiang,Qian Jixin.An optimizing method based on autonomous animals:fish-swarm algorithm [J].Theory&Practice,2002,22(11):32-38.
李晓磊,邵之江,钱积新.一种基于动物自治体的寻优模式:鱼群算法[J].系统工程理论与实践,2002,22(11):32-38.
[10] Wang Lianguo,Shi Qiuhong.Parameters analysis of artificial fish swarm algorithm [J].Computer Engineering,2010,36(24):169-171.
王联国,施秋红.人工鱼群算法的参数分析[J].计算机工程,2010,36(24):169-171.

