相位编码光学加密算法的扩散及混淆特性分析

林 超，沈学举，王昭辉，曹端超，赵 诚

引言

光学信息安全技术是20世纪90年代兴起的新一代信息安全技术之一。由于光学信息处理系统具有高速二维并行处理以及多加密自由度等优点，光学信息安全技术在近几年得到快速发展。许多新的光学加密算法被提出［1］，对经典光学加密算法的深入分析也在同时展开，其中以对双随机相位编码（double random phase encoding，DRPE）［1］算法的研究最为全面和深入［2－4］。例如，对 DRPE算法抵抗选择密文［5］、选择明文［6］、已知明文［7］以及唯密文［8］攻击性能的研究揭示了该算法的线性本质［9］，据此，通过在算法中引入非线性变换来提高其抗攻击性能的方法也被提出［10］。此外，都柏林大学的研究人员深入研究了DRPE算法在光学实现中表现出的特性以及产生的具体问题，DRPE算法的统计特性［11］、算法的密钥空间［12］、算法的碰撞安全性［13］、解密过程中对密钥的敏感性［14］以及振幅编码和相位编码模式下算法的安全性［15］等也被深入研究。

上述研究成果使人们对DRPE算法的本质有了深入的理解。但是，结合现代密码学理论对DRPE算法的安全性进行评估的研究尚未完全展开。由于DRPE算法属于对称分组密码算法，根据现代密码学基本理论［16］，算法对明文信息的扩散和混淆程度决定了其在统计学意义上的安全性。现代密码学理论认为，即便一个密码算法能够抵抗各种具体的攻击，但是随着数字设备计算能力的极大提升，任何一个密码算法都可能被攻击者通过统计分析或者穷举分析的形式获得其密钥或者算法的重要参数，虽然DRPE算法可以生成的密文符合平稳白噪声分布［1］，但是，其密文的灰度分布仍然可能泄露明文或者系统信息。因而，如何避免通过分析密文的统计特性来恢复算法的密钥等信息成为密码算法设计中必须考虑的重要问题。本文采用分组密码设计准则来分析DRPE算法的扩散和混淆特性，该研究不仅可以阐明一般情况下采用随机相位作为密钥的光学加密算法的分组密码学本质，还可以为光学加密算法的设计提供一定的参考。

我们首先引入了现代密码学中有关分组密码的设计准则，然后将DRPE算法分解为几个过程来分析，分析了算法生成密文的统计分布特性，提出采用信息熵来评价密文统计特性的好坏，揭示了该算法的扩散及混淆本质，又将傅里叶变换域、菲涅尔变换域以及分数阶傅里叶变换域随机相位加密算法的扩散和混淆特性进行了比较和分析。理论分析和数值模拟结果取得了较好的一致性。

1 分组密码设计准则

分组密码是指把明文序列按固定长度进行分组，用相同的密钥和加密算法逐组进行加密的密码体制。Shannon提出了分组密码的基本设计原则，即扩散和混淆原则。

扩散是将每一位明文和密钥的影响尽可能迅速地作用到输出的密文所有位上，以隐藏密文的统计特性。良好的扩散可以防止攻击者将密钥分解成各个孤立的部分逐个击破。混淆是指密文与明文之间的等价数学关系复杂并难以破解。仅靠扩散进行加密可能使明文和密文间满足某种线性关系，而线性关系容易被破解。因此还要通过混淆算法使明文和密文间的关系复杂化。

基于光学原理的加密算法大都属于分组密码的范畴，光学流密码的算法种类不多。因此，根据分组密码编码学和分组密码分析学分析已有光学加密算法的安全性并设计满足扩散和混淆原则的新的光学密码系统对于提高光学加密算法的安全性很有意义。

2 傅里叶域随机相位加密算法扩散混淆特性分析

2.1 理论分析

根据上述关于分组密码设计准则的阐述，光学加密算法作为一种分组密码，应满足Shannon提出的分组密码设计准则，下面先分析傅里叶域双随机相位光学加密算法的扩散和混淆特性。

双随机相位光学加密算法生成的密文的统计特性依赖于扩散和混淆的程度和轮数，由于该算法不含迭代过程，因此不存在轮数的问题，其单次加密对明文信息的扩散和混淆程度决定了由该算法生成的密文的统计特性，进而决定了其统计学意义上的安全性［16］。通常，线性变换会在一个密码系统中引入扩散特性而非线性算法引入混淆特性。在现代密码学中，换位算法属于一种典型的线性算法而代换算法是典型的非线性算法。用f（x，y）表示原始图像，ψ（x，y）表示加密后的图像，a（x，y）和b（u，v）分别表示相互独立的均匀分布在［0－1］的随机白噪声序列，则DRPE算法的数学描述为

式中：F表示傅里叶变换；F－1表示傅里叶逆变换；x和y表示空域坐标；u和v是频域坐标。

该算法的加密过程可以看成通过2个级联的2－f系统对输入图像进行变换得到加密后图像的过程。由于第2个2－f系统所做的傅里叶逆变换可以通过对密图直接做傅里叶变换进行抵消，因而这一逆变换本质上没有进行加密。下面根据分组密码设计准则及傅里叶变换的性质分析第1个2－f系统对输入图像的变换。先给出通过分析得到的下述结论：

1）傅里叶变换通过代换的形式在DRPE算法中引入了混淆操作；

2）随机相位模板结合傅里叶变换通过换位的方式在DRPE算法中引入了扩散操作。

下面根据傅里叶变换的相关理论分别分析上述两条结论。

傅里叶变换将原始图像f（x，y）变换成了其频谱，这可以理解为用原始图像的频谱信息代替了原始图像信息，属于基于代换的混淆操作。但是这个代换算法没有密钥控制，因而很容易通过逆傅里叶变换恢复原始图像。

在2－f系统的输入面，输入原始图像和空域随机相位模板相乘相当于在输入图像上叠加了随机相移。所谓随机相移，是指相移在输入面产生的位置和相移量具有随机性的相移。因为随机相位模板的相位分布是随机的，根据角谱传播理论［19］，可以把随机相位模板看成具有把输入平面波变成沿不同方向传播的平面波谱功能的光学元件，在随机相位模板的参数满足一定条件后，随机相位函数的傅里叶谱就随机均匀的分布在整个谱平面。

把输入图像分割成很多小的输入图像的加和，如图1（a）所示，在数学上不难理解，则原始输入图像的傅里叶变换谱可以看成分割而成的小的如图1（b）所示的输入图像分别进行傅里叶变换后谱的加和。图1（d）表示随机相位模板的相位分布，图1（e）所示为局部放大后的随机相位分布，当输入图像分割成的子图像较小时，由于随机相位分布的连续性，可以把和子图像部分进行叠加的随机相位函数近似成常数相移，则根据傅里叶变换的位移和相移性质，空域的相移在频域会引入位移，空域的位移在频域引入相移，则2－f系统频谱面的复振幅分布可以认为是输入图像的子图像的谱在引入了相移和位移后的叠加。图1（c）及图1（f）分别为局部原始图像图1（b）的傅里叶谱以及叠加了常数相移的局部原始图像的傅里叶谱，其定性描述过程如下：

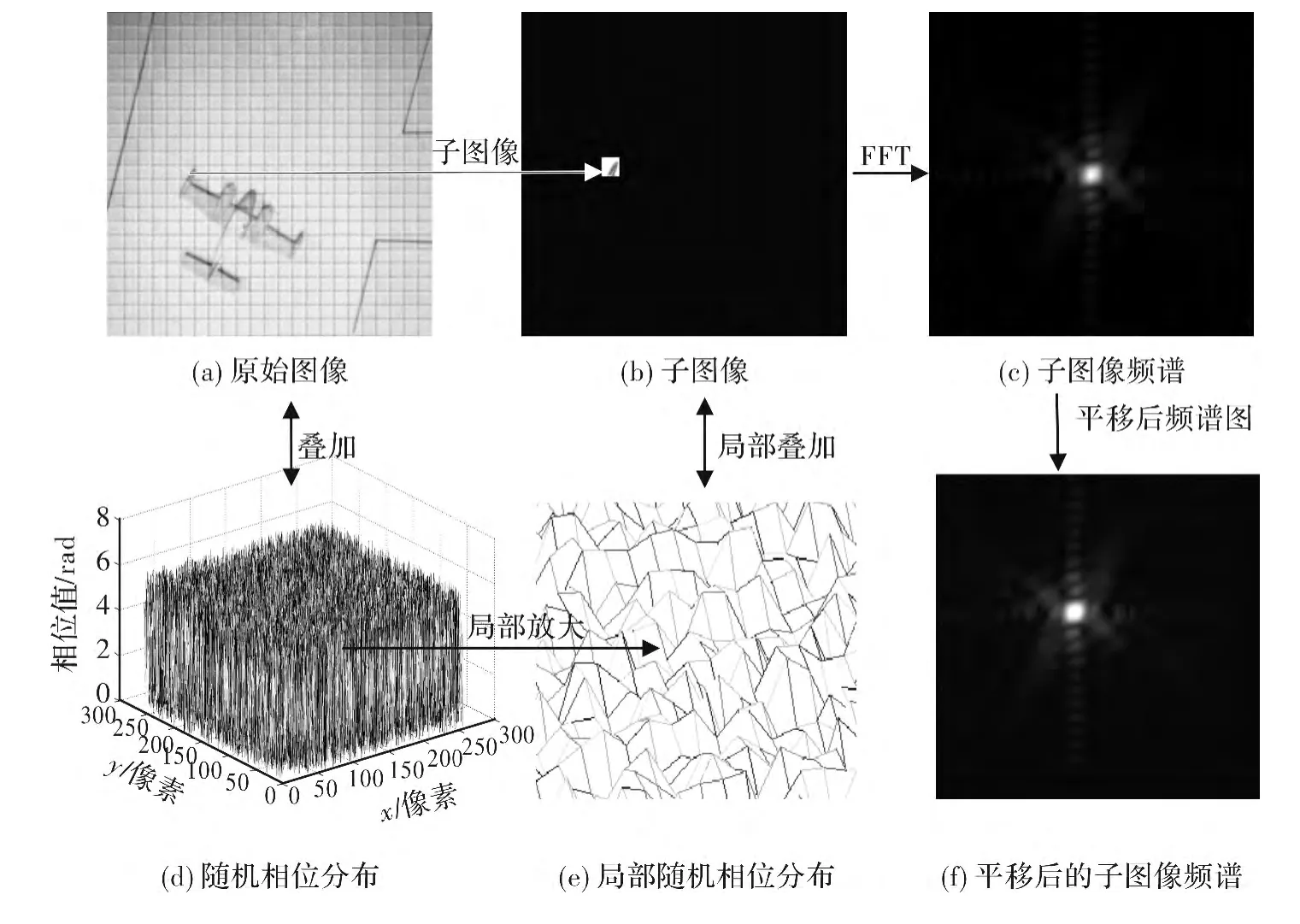
图1 2－f单随机相位加密系统扩散操作示意图Fig.1 Diagram of diffusion operation in 2－f single random phase encoding system

式中：i表示“第i个子图像”，如图1（a）所示，其编号顺序从上至下从左至右依次递增；gi（u，v）表示fi（x，y）的傅里叶变换；（ui，vi）表示由空域随机相移引起的频域随机位移量；φi表示由空域位移（xi，yi）引入的频域相移量。由于空域位移（xi，yi）和原始图像分割成子图像的方式无关，且该过程没有随机性，因而对加密来说影响较小。而由空域随机相位函数引入的频域位移具有随机性，因而对加密过程来说至关重要。

通过上述分析可知，由空域随机相位函数结合傅里叶变换而引入的频域随机换位是随机相位加密算法的核心操作，其中的随机相位函数是算法的密钥，由于换位算法属于线性算法，因而随机相位加密算法中主要的随机化操作为扩散操作，而没有在密钥控制下的混淆操作，因而从统计学意义来看，随机相位光学加密算法安全性不是很高。

4－f系统可以看成是2－f系统的级联，原始图像经过2－f系统变换后和经过4－f系统变换后得到的图像统计特性是近似相同的，图2给出了2－f单随机相位加密系统和4－f双随机相位加密系统输出图像的直方图分布，可以看出，两个系统输出图像的直方图分布相似度很高，但是由于2－f单随机相位加密系统的输出图像可以通过傅里叶逆变换和取模操作恢复出原始图像，因而在实际应用中起不到加密的作用，4－f双随机相位加密系统通过频谱面随机相位函数对2－f系统的输出进行调制而掩盖了2－f单随机相位加密算法输出复振幅的相位信息，因而能起到加密的作用。

上述理论分析不仅阐明了随机相位函数在DRPE算法中的作用，也间接证明了随机振幅函数由于不能引入换位操作而不能作为基于4－f系统加密算法的密钥，但是通过设计特定结构的加密系统，随机振幅函数仍然有可能作为密钥使用［17］。

图2 2－f系统（a）和4－f系统（b）随机相位加密输出图像直方图Fig.2 Histograms of output images with 2－f and 4－f random phase encoding systems

2.2 仿真结果

下面通过数值模拟的方式验证上述理论分析及预测。分别对傅里叶域单随机相位、双随机振幅、双随机相位加密算法进行了模拟。基于MATLAB7.6平台，输入原始图像为256×256像素的灰度图像，如图3（a）所示，入射光波长设为632.8nm，仿真结果如图3所示。

图3 2－f系统及4－f系统随机相位及随机振幅加密图Fig.3 Images of random phase and random amplitude encoding with 2－f and 4－f system

仿真结果进一步证实了采用随机振幅模板得不到均匀白噪声部分的加密图像，如图3（c）所示。而采用随机相位模板在2－f系统及4－f系统结构下可以得到较好的加密图像，如图3（b）和图3（d）所示。

引入信息熵来评价加密图像的不确定性。信息熵可以反映信息的不确定性，一幅图像的信息熵定义如下［18］：

式中：pi表示图像中灰度值为i的像素出现的概率；L为图像的灰度等级。对于一般的灰度图像L＝256，则信息熵的最大值为8。一般认为，一幅图像的信息熵越大，该图像中灰度分布越均匀，对于攻击者来说越难通过统计分析恢复出原始图像信息，加密效果越好。经过计算，图3（b）、图3（c）和图3（d）的信息熵分别为7.038、4.521和7.157，这表明采用双随机相位加密算法和单随机相位加密算法能得到灰度分布更均匀的加密图像，而采用随机振幅模板则得不到统计特性较好的加密图像。

3 菲涅尔域及分数阶傅里叶变换域分析

3.1 理论分析

菲涅尔域及分数阶傅里叶变换域DRPE算法由于分别引入了衍射距离以及分数阶次作为额外的密钥可以增强基于4－f系统DRPE算法的安全性，但是其分组密码特性没有本质改变。下面分析菲涅尔域和分数阶傅里叶变换域随机相位加密算法的扩散特性。菲涅尔变换可以用傅里叶变换来表示［19］：

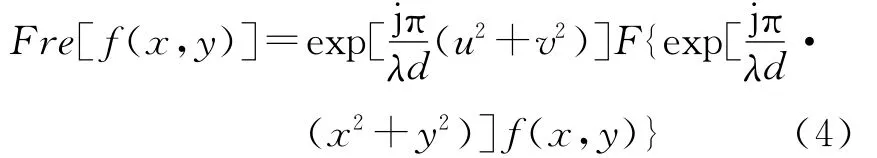
式中：Fre表示菲涅尔变换；λ表示光波长；d为菲涅尔衍射距离。上式表明一幅图像的菲涅尔变换相当于该图像和一个二次相位因子乘积的傅里叶变换之后的结果再乘以一个二次相位因子。因而，（4）式中傅里叶变换内的二次相位因子也能起到类似于随机相位函数的作用，只是由于二次相位函数的对称性，该二次相位因子能引入一种规则的换位操作。

分数阶傅里叶变换与菲涅尔变换的关系有一定的联系［19］，设函数U2（x2）为函数U1（x1）的菲涅尔衍射变换，则一维分数阶傅里叶变换可以用菲涅尔变换表示为

由（5）式可知，一幅图像的分数阶傅里叶变换可以由其菲涅尔变换经过坐标缩放和相位调制后得到，因而，分数阶傅里叶变换引入扩散操作的特性和菲涅尔变换类似。

由于菲涅尔变换和分数阶傅里叶变换本身的二次相位调制作用，使得在菲涅尔域和分数阶傅里叶变换域的随机振幅加密成为一种可能的加密方法。

3.2 仿真结果

通过数值模拟的方式分别对菲涅尔域单随机振幅、双随机振幅加密算法，分数阶傅里叶变换域单随机振幅、双随机振幅加密算法进行了模拟。输入原始图像为256×256像素的灰度图像，如图3（a）所示，入射光波长设为632.8nm，菲涅尔衍射距离设为0.3m。菲涅尔域随机振幅加密图像如图4（a）及图4（b）所示。

图4 菲涅尔域随机振幅加密图像Fig.4 Encrypted images of random amplitude encoding in Fresnel domain

从图4可以看出，菲涅尔域随机振幅算法得到的是网格状的引入了规则换位操作的加密图像。加密图像虽然在一定程度上能掩盖原始图像信息，但不是平稳白噪声分布，容易被破解。

分数阶傅里叶变换域随机振幅加密图像如图5所示。

图5 分数阶傅里叶变换域随机振幅加密图像Fig.5 Encrypted images in fractional Fourier domain with random amplitude encoding

图5 （a）～（c）分别为分数阶傅里叶变换域单随机振幅加密图像，其中分数阶次分别为0.5、0.7、0.9。图5（d）～（f）分别为分数阶傅里叶域双随机振幅加密图像，其中分数阶数分别为0.5、0.7、0.9。可以看出，分数域随机振幅加密结果呈现出了随着分数阶数变化密图按比例缩放的特性，这与分数阶傅里叶变换和菲涅尔变换的关系函数相符合。

以上的仿真结果在一定程度上表明了对不同变换域随机相位及随机振幅加密的扩散混淆特性分析是合理的。

4 结论

基于傅里叶变换的位移和相移性质，从分组密码设计准则出发，分析了基于随机相位模板的光学加密算法的扩散和混淆特性。通过理论分析和数值模拟，可以得到以下结论：

1）相位编码光学加密算法主要通过在空域引入随机相移，进而在频域对局部原始图像的谱实现随机换位操作来达到对原始图像信息的扩散目的，其中的随机相位函数是控制扩散过程的参数，即系统密钥。这一研究结果揭示了相位编码光学加密算法的分组密码本质，对于设计安全性更高的光学分组密码系统具有一定意义。

2）相位编码光学加密算法仅存在基于傅里叶变换的混淆操作，缺乏具有密钥控制的基于复杂代换算法的混淆操作，密文的统计特性不甚理想，存在被攻击和破解的可能。

3）菲涅尔变换域和分数阶傅里叶变换域相位编码加密算法虽然引入了衍射距离和分数阶数作为额外密钥，但是并没有改变相位加密算法以扩散操作为主的分组密码本质，密文统计特性依然不够理想。虽然光学加密技术相对于传统密码算法具有诸多优势，但是其安全性还有待于通过引入复杂的扩散和混淆操作来进一步提高。

［1］ Philippe R，Bahram J.Optical image encryption based on input plane and Fourier plane random encoding［J］.Optics Letters，1995，20（7）：767－769.

［2］ Bahram J，Zhang Guan－shen，Li Jian.Experimental demonstration of the random phase encoding technique for image encryption and security verification［J］.Optical Engineering.1996，35（9）：2506－2512.

［3］ Hennelly B，Sheridan J.Optical encryption and the space bandwidth product ［J］.Optics Communications，2005，247（1）：291－305.

［4］ Sarkadi T，Koppa P.Quantitative security evaluation of optical encryption using hybrid phase and amplitude－modulated keys［J］.Applied Optics，2012，51（6）：745－750.

［5］ Carnicer A，Montes－Usategui M，Arcos S，et al.Vulnerability to chosen－cyphertext attacks of optical encryption schemes based on double random phase keys［J］.Optics Letters，2005，30（13）：1644－1646.

［6］ Lin Chao，Shen Xueju.Analysis and design of impulse attack free generalized joint transform correlator optical encryption scheme［J］.Optics and Laser Technology，2012，44（1）：2032－2036.

［7］ Gopinathan U，Monaghan D，Naughton T，et al.A known－plaintext heuristic attack on the Fourier plane encryption algorithm ［J］.Optics Express，2006，14（8）：3181－3186.

［8］ Peng Xiang，Tang Hongqiao，Tian Jiandong.Ciphertext－only attack on double random phase enco－ding optical encryption system［J］.Acta Physica Sinica，2007，56（5）：2629－2636.

彭翔，汤红乔，田劲东.双随机相位编码光学加密系统的唯密文攻击 ［J］.物理学报，2007，56 （5）：2629－2636.

［9］ Frauel Y，Castro A，Naughton T，et al.Resistance of the double random phase encryption against various attacks ［J］.Optics Express，2007，15（16）：10253－10265.

［10］ Wang Xiaogang，Zhao Daomu.Multiple－image encryption based on nonlinear amplitude－truncation and phasetruncation in Fourier domain ［J］.Optics Communications，2011，284（1）：148－152.

［11］ Monaghan D，Gopinathan U，SiTu Guohai，et al.Statistical investigation of the double random phase encoding technique［J］.Journal of Optical Society of America A，2009，26（9）：2033－2042.

［12］ Monaghan D，Gopinathan U，Naughton T，et al.Key－space analysis of double random phase encryption technique［J］.Applied Optics，2007，46（26）：6641－6647.

［13］ SiTu Guohai，Monaghan D，Naughton T，et al.Collision in double random phase encoding［J］.Optics Communications，2008，281（1）：5122－5125.

［14］ Monaghan D，SiTu Guohai，Gopinathan U，et al.Role of phase key in the double random phase encoding technique：an error analysis［J］.Applied Optics，2008，47（21）：3808－3816.

［15］ Monaghan D，SiTu Guohai，Gopinathan U，et al.Analysis of phase encoding for optical encryption［J］.Optics Communications，2009，282 （1）：482－492.

［16］ Wu Wenling，Feng dengguo，Zhang Wentao.Design and analysis of block cipher［M］.Beijing：Tsinghua University Press，2009.

吴文玲，冯登国，张文涛.分组密码的设计与分析［M］.北京：清华大学出版社，2009.

［17］ Lin Chao，Shen Xueju.Multiple images encryption based on Fourier transform hologram ［J］.Optics Communications，2012，285（1）：1023－1028.

［18］ Rodriguez J.Computational cryptography based on trigonometric algorithms and intensity superposition［J］.The Imaging Science Journal，2010，58（1）：61－80.

［19］ Goodman J.Introduction to Fourier Optics ［M］.New York：McGraw－Hill，1988.