肥大型船舶伴流分数的估算方法研究

，， ，，

(哈尔滨工程大学 船舶工程学院，哈尔滨 150001)

出于对节能环保方面的考虑，国际海事组织于2013年强制执行了EEDI(船舶能效设计指数)，作为主力运输船型的肥大型船将不得不进行调整以适应新的标准[1]。在这种情况下，准确快速地预报船舶的推进性能，并在此基础上对船型加以改型或优化就显得尤为重要。在船舶推进性能预报以及螺旋桨设计的过程中，伴流分数的预报是必不可少的一环，其精度直接影响结果的好坏[2]。本文应用传统伴流分数估算公式进行计算并分析其结果，在此基础上选定部分船型参数及无因次量，提出线性数学模型，通过逐步回归法得到一种新的，更加精确的伴流分数估算方法[3-6]。

1 传统伴流分数估算公式

本文选取:①泰勒公式;②汉克歇尔公式;③巴甫米尔公式;④霍尔特洛泼公式;⑤荷兰船模水池公式;⑥BSRA系列自航要素计算法;⑦SSPA系列自航要素计算法;⑧SSPA修正方法[7-9],对某型35 000 DWT散货船、某型48 000 DWT油船、某75 000 DWT散货船、某115 000 DWT油船、某82 000 DWT散货船等数十艘肥大型船进行计算，部分结果见表1、表2。

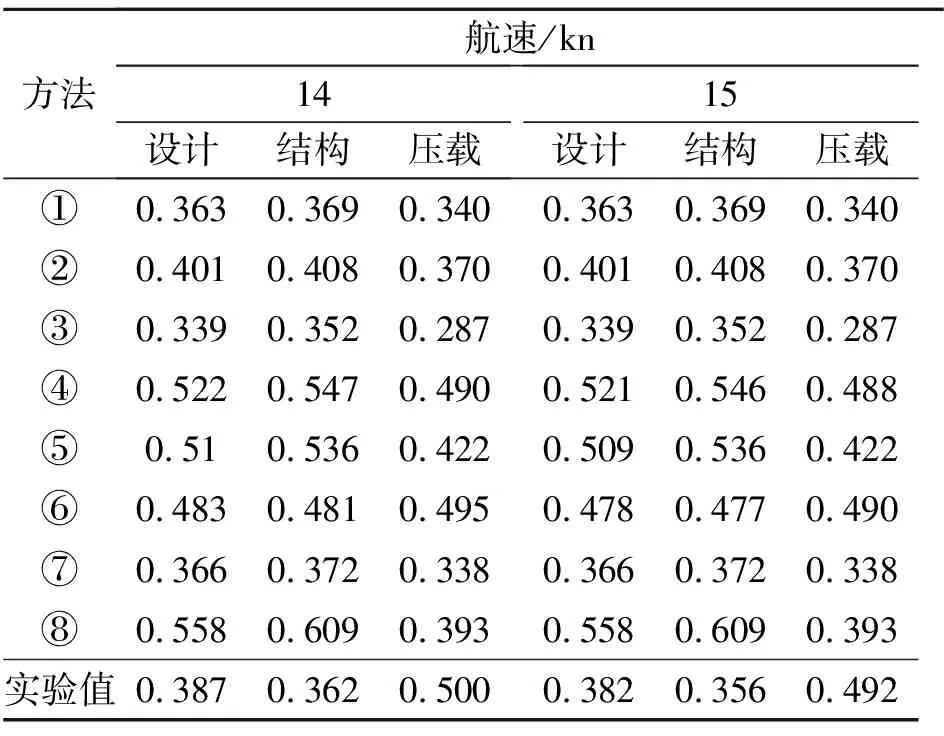
表1 某48 000 DWT油船伴流分数估算数据

表2 某82 000 DWT散货船伴流分数估算数据

结合公式得出以下结论。

1)设计和结构吃水状态下，①②③⑦公式估算效果更好。

2)压载吃水情况下，各公式估算效果不稳定。

3)从实验值可以看出w压载>w设计>w结构，而T结构>T设计>T压载，需认为吃水或者排水量对伴流分数有一定的影响，除式⑥以外的公式都不能很好地解释这一变化。

4)从实验值可以看出，伴流分数随速度的增加会略微减少。定性分析，速度的增加使得雷诺数变大，边界层的厚度减小，摩擦阻力减小，摩擦伴流也随之减小。但除式④⑤⑥以外的公式都不能解释这一现象。

5)①②这种单一变量组成的公式并不能很好地解释伴流分数的变化，只能初估其数值。

6)设计、结构两种吃水状态由于吃水改变较小，伴流分数值并无较大变化。

7)总体来看，有的伴流公式仅表示与船型参数有关，有的公式虽考虑了航速对伴流的影响，但是难以反应肥大型船不同吃水状态下伴流分数变化的规律，计算的精确度也都不是很好。

2 回归分析

对于肥大型船来说，传统伴流分数估算公式的精度并不能令人满意，原因之一在于这一船型的应用与发展主要集中在近20年，很多估算公式的年代都比较久远，考虑的船型十分有限，并不能满足现代造船的要求;原因之二则是部分估算公式在船型参数及无因次量的选取上考虑不够全面。因此，以大量现代船舶试验数据为基础，考虑多个影响因素，通过回归分析的方法得到适用于肥大型船的估算公式是十分有意义的。

2.1 确定备选变量

从伴流的成因来考虑，可将其分为三部分。其中，摩擦伴流是由于真实液体存在黏性，导致船体周围的边界层内水质点具有向前的速度而产生的伴流。对肥大型船来说，由于航速较低，摩擦伴流是伴流的主要部分，故引入黏性阻力系数Cv来考虑黏性影响。波浪伴流是由船体本身兴波作用产生的伴流，一般在弗劳德数Fr大于0.3时起作用，对肥大型船的影响并不大，出于回归精度考虑也将Fr选为变量之一。

在此基础上，借鉴传统伴流分数估算公式，初步确定备选变量为黏性阻力系数Cv、Fr、长宽比L/B、宽度吃水比B/T、直径吃水比D/T、螺距比P/D、长度排水量无因次比L/▽1/3、方形系数Cb以及菱形系数Cp。

2.2 建立回归模型

经过简单的相关分析，除伴流分数与直径吃水比和纵向浮心位置的线性关系不显著外，其他相关系数均在0.01显著性水平上显著。因此可以建立多元线性回归模型去拟合伴流分数与各变量之间的关系，在求出回归方程后, 再对回归方程及回归系数进行检验。

w=a0+a1Cv+a2Fr+a3L/B+a4B/T+

a5D/T+a6P/D+a7L/▽1/3+a8Cb+

a9Cp+a10Lcb

2.3 逐步回归法

虽然变量选取基于伴流成因分析并借鉴了传统公式，但并不能保证对伴流分数都有显著的影响。为从较多的初选自变量中选择出一些作用较大的因子, 获得最优回归方程, 可以借助逐步回归分析方法对自变量进行筛选。

2.4 回归结果及检验

根据数十艘肥大型船试验资料，进行简单的数据处理，形成多个多维样本，使用SPSS软件进行多元线性回归，回归结果见表3～5。

表3 模型汇总

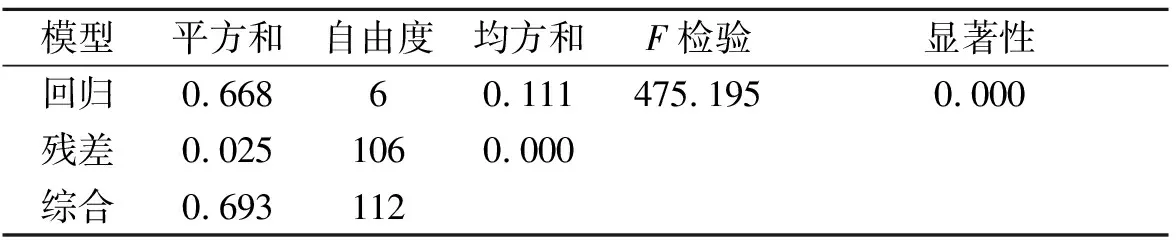
表4 方差分析

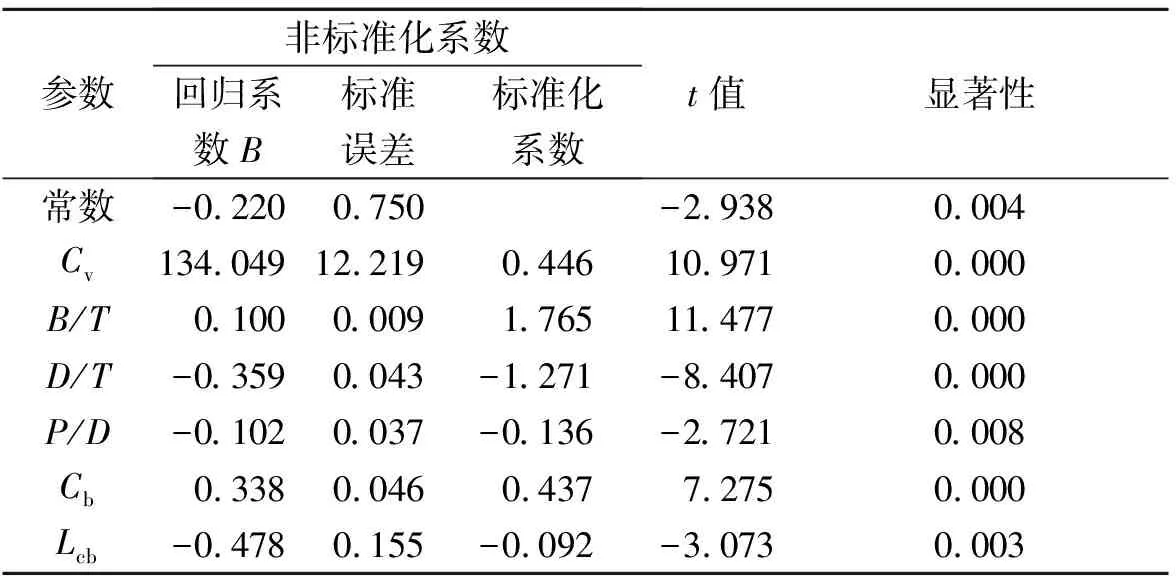
表5 回归系数

弗劳德数Fr、长宽比L/B、长度排水量无因次比L/▽1/3及菱形系数Cp等4个变量由于对伴流分数影响不显著或是多重共线性的原因均被剔除，不予应用。

如表3模型汇总所示，复相关系数R=0.982，决定系数R2=0.964，调整后决定系数R2=0.962，从调整后决定系数看，回归公式高度显著。

如表4，F=475.195，p=0.000，表明回归方程高度显著，说明自变量对伴流分数有高度显著的线性影响。

如表5，回归系数的显著性检验，自变量对伴流分数均有显著影响，螺距比P/D中的P=0.008最大，但仍在1%的显著性水平上对伴流分数产生影响。

经过残差分析，所得结果可以满足回归模型假设，且不存在异方差问题。综上所述，可以认为回归方程是有效可靠的。

3 伴流分数预报

应用回归所得公式对部分肥大型船进行伴流分数的预报，结果见表6～8。

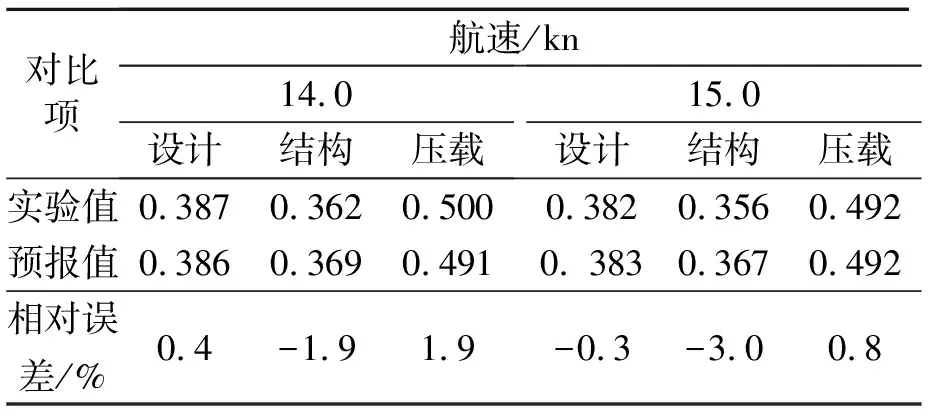
表6 某48 000 DWT油船伴流分数估算数据

表7 某75 000 DWT散货船结构吃水状态伴流分数估算数据

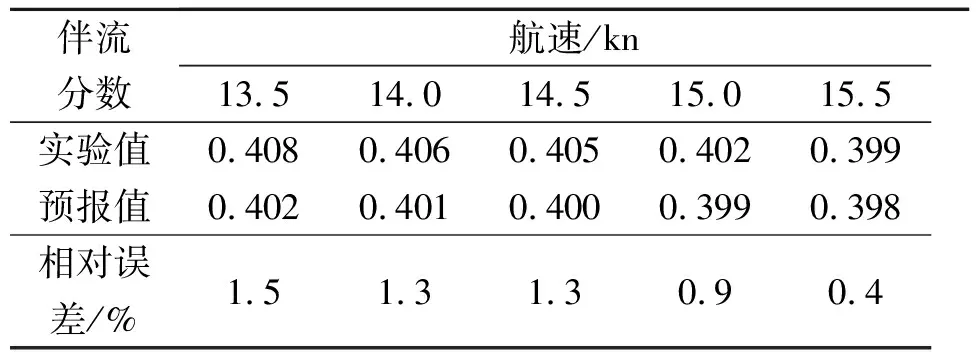
表8 某115 000 DWT油船设计吃水状态伴流分数估算数据

通过回归方法得到的估算公式相比于传统经验公式，估算精度有了显著提升，实验值和估算值之间的相对误差也大大减小。从以上3艘船的3个浮态的计算结果来看，75 000 DWT的估算相对误差最大，也不超过10%，对于初步设计来说，这一精度已经符合要求。从公式的形式和结果上来看，也可以解释吃水和航速对肥大型船伴流分数的影响，验证了在Fr<0.3的情况下，波浪伴流的影响很小。

4 结论

对于肥大型船来说，传统伴流分数估算公式的精度比较差，并且公式的形式与算法并未体现出一些实验中观测到的结论，单一考虑或者不考虑Cb，D/T等部分船型参数及螺旋桨参数是不妥的。

对于肥大型船来说，本文得到的估算公式的精度有了显著的提升，能反应部分伴流分数变化规律，且更加符合现代船舶技术水平，可为新船的初步设计提供帮助。

应用传统估算方法必须针对其研究对象，经过公式形式或部分参数的修正，并进行数据验证，才能保证其科学性。

由于数据量的缘故，此公式并未完善其变量的变化范围，仅根据肥大型船定义Cb>0.8，适用性还有待进一步研究完善。

[1] 刘 飞,林 焰,李 纳,等.我国船舶EEDI分析研究[J].中国造船,2012,53(4):128-136.

[2] 陈昌运,陈霞萍.螺旋桨直径对伴流分数的影响研究[C]∥2008年船舶水动力学学术会议暨中国船舶学术界进入ITTC30周年纪念会,杭州,2008.11.中国造船,2008:169-171.

[3] SCHNEEKLUTH H,BERTRAM V.Ship design for efficiency and economy[M].London,Britain:Butterworth-Heinemann,1998.

[4] 王国强,盛振邦.船舶推进[M].上海:上海交通大学出版社,2004.

[5] 陈可越.船舶设计实用手册[M].北京:中国交通科技出版,2007.

[6] 周占群,谢克振,胡 平,等.大型油船航速估算方法[J].中国造船,1994(4):1-12.

[7] 周连第.多元回归分析方法及在船舶科研设计中的应用[M].北京:国防工业出版社,1979.

[8] 程红蓉,何术龙,王艳霞,等.大型运输船舶快速性能回归分析研究[J].中国造船,2010,51(1):27-36.

[9] 冯 力.回归分析方法原理及SPSS实际操作[M].北京:中国金融出版社,2004.