肥大型船舶阻力计算方法修正

， ， ，

(哈尔滨工程大学 船舶工程学院，哈尔滨 150001)

准确预报船舶阻力是船舶设计工作者的重要任务之一[1]。在船舶设计的初级阶段，由于船舶线型尚未确定，因而不能用船模试验或者CFD方法来确定阻力，只能用传统的阻力计算方法来近似估算，以选择合适主机，保证船舶能够到达设计航速，或者在主机确定的情况下，预估阻力以确定航速。这一过程需要将船舶的主尺度和主要船型参数相结合，考虑多参数变化的影响，预报多种情况下的船体阻力，再对各种方案进行反复论证，最终得到满足使用要求且阻力最小的船型。而在这一过程中，快速、准确地预报各种不同参数下的船体阻力是一项极其关键，同时又是相等困难的工作。但随着船舶阻力和推进学科的发展及新船型的不断出现，传统的阻力预报方法已经不能准确预报船舶阻力。特别是近些年肥大型船舶的出现，很多新造船舶都超出了传统图谱和各种经验公式的使用范围[2]。

本文结合系列化试验阻力图谱对部分肥大型船舶进行阻力计算，并在分析计算值与试验值误差的基础上运用函数拟合的方法得到阻力修正因子与船型参数的函数关系式，从而提出一种适用于肥大型船舶阻力的计算方法[3-7]。

1 肥大型船舶的阻力计算

传统的船舶阻力计算方法根据弗劳德假定将船舶总阻力分为摩擦阻力和剩余阻力两部分，其中剩余阻力用兰坡凯勒图谱计算，摩擦阻力按照桑海公式计算，而粗糙度补贴系数根据荷兰试验水池发表的数据进行实船粗糙度和尺度效应的补贴换算。

根据项目合作单位提供的48 000 t油船、115 000 t油船，大连中远船务提供的35 000 t散货船、82 000 t散货船的船型设计及船模试验资料，包括船型设计参数(垂线间长、型宽、型深、设计吃水、排水量、方形系数、菱形系数、湿表面积、浮心纵向位置等)，船模静水阻力试验报告，运用传统方法对船舶的阻力进行计算，然后将计算值与船模试验值进行比较。见表1～5。

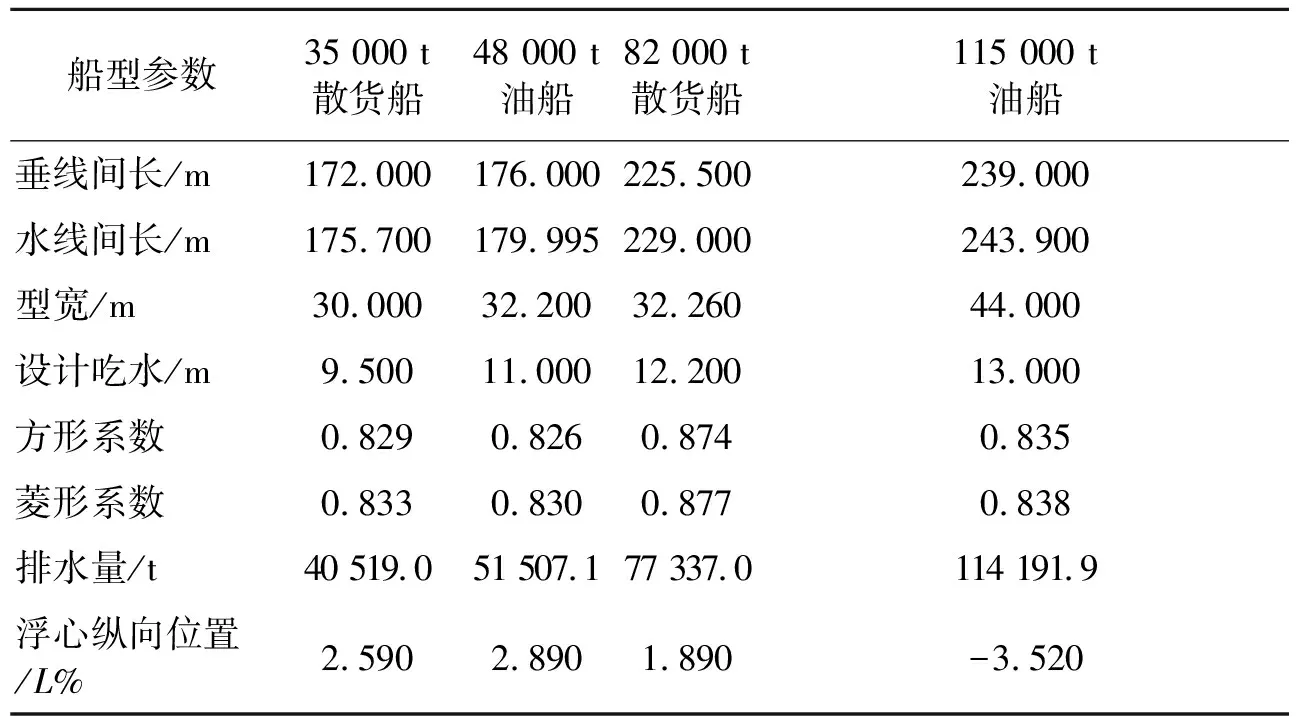
表1 肥大型船舶主要设计参数

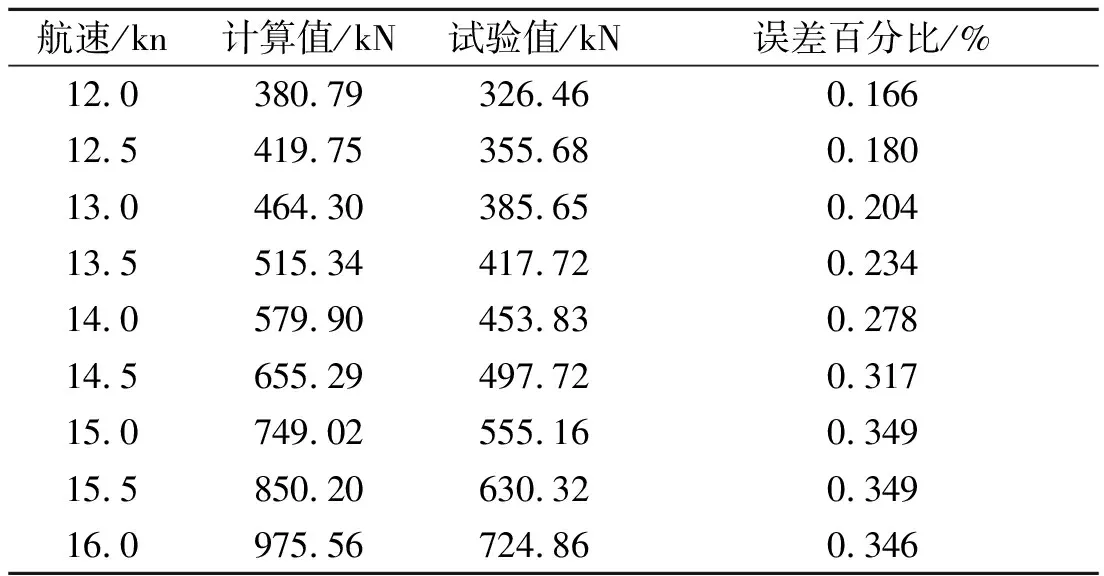
表2 35 000 t散货船阻力计算值和试验值对比

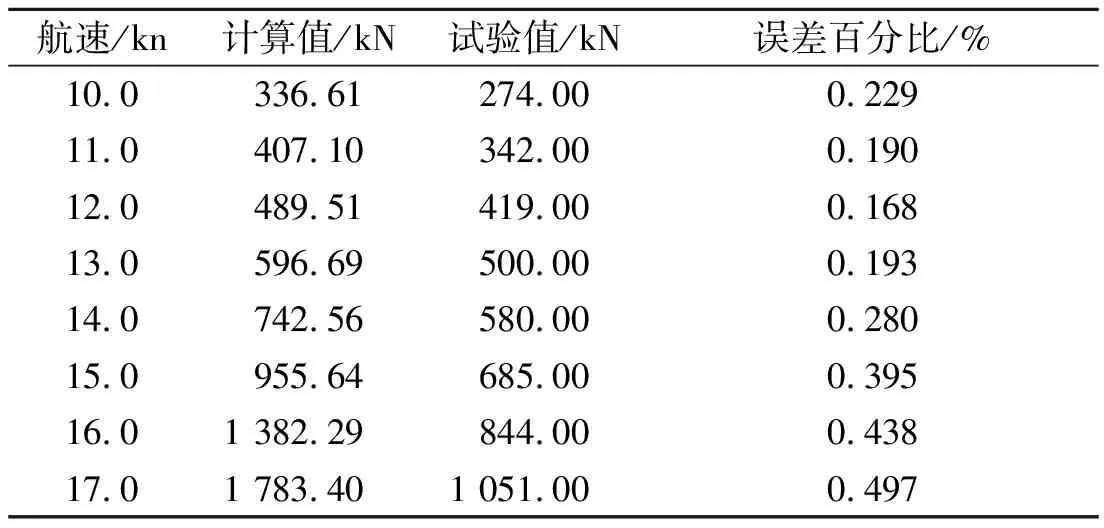
表3 48 000 t油船阻力计算值和试验值对比

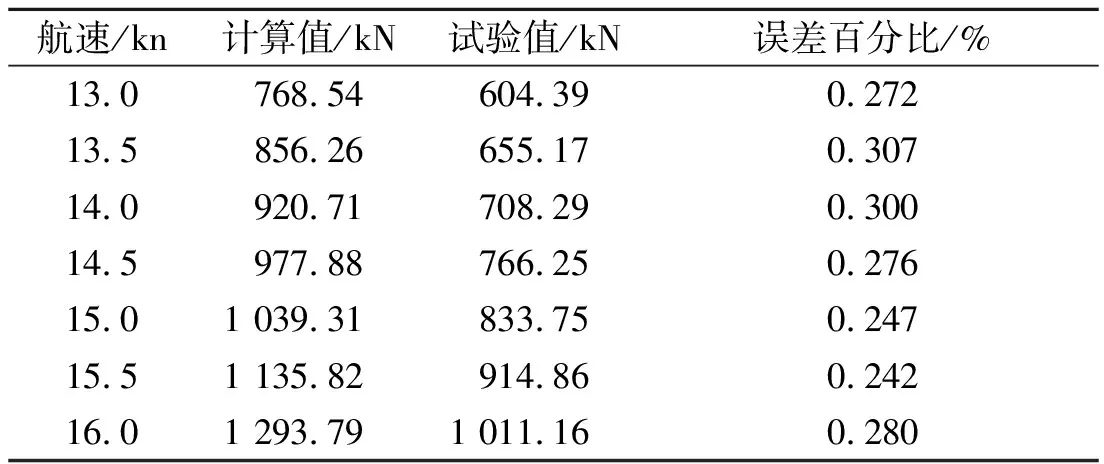
表4 82 000 t散货船阻力计算值和试验值对比

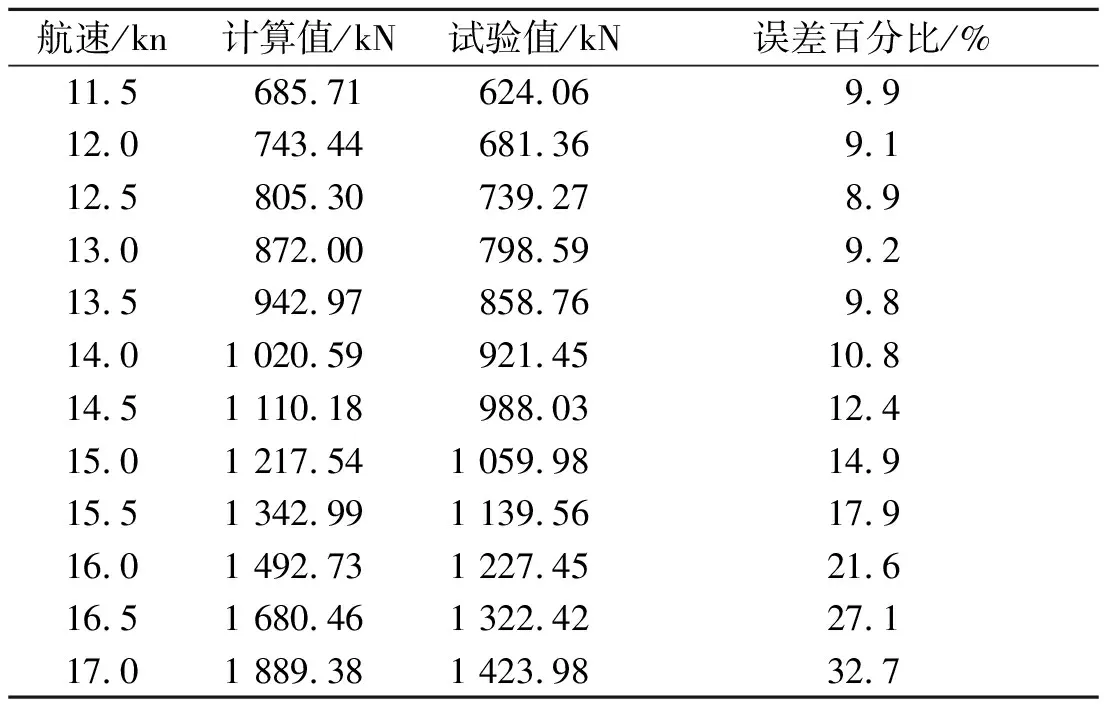
表5 115 000 t油船阻力计算值和试验值对比

由表2～5可见，传统阻力计算值和试验值的误差百分比一般在10%～50%之间，且随着航速的增大，误差会随之增大，达不到工程上的应用，有必要进行计算方法的修正。

2 阻力计算的误差分析

2.1 摩擦阻力计算分析

1932年桑海运用对数速度分布规律，并根据平板拖曳试验结果，给出摩擦阻力计算公式。1947年美国船模试验池会议将其作为计算摩擦阻力的标准公式，成为1947ATTC公式。

(1)

式中:ρ——海水密度,kg/m3;

S——船体湿表面积,m;

V——船速,m/s;

Cf——摩擦阻力系数，用桑海公式计算：

(2)

其中:Re——雷诺数。

我国以往取粗糙度补贴系数ΔCf=0.000 4，对于船长为100 m左右的船舶，取ΔCf=0.000 4所得结果与实船试验基本相符。但是，不同船长的船舶试航结果表明，ΔCf值将随船长增加而趋减小，直至出现负值。荷兰水池1973年发表了随船长变化的ΔCf值，见表6.

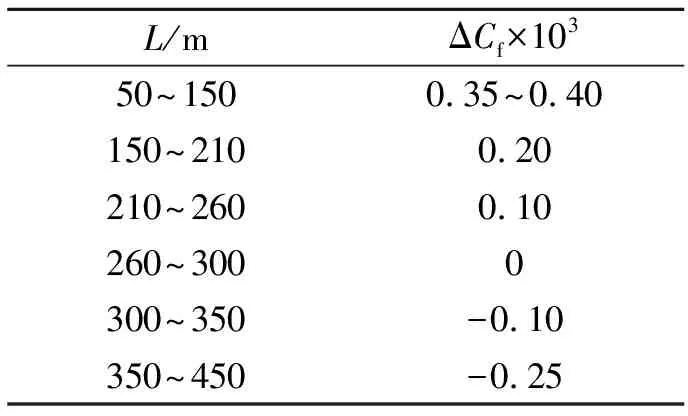
表6 不同船长下ΔCf的取值

日本船舶研究所用桑海公式时的相关系数Ca值见表7。

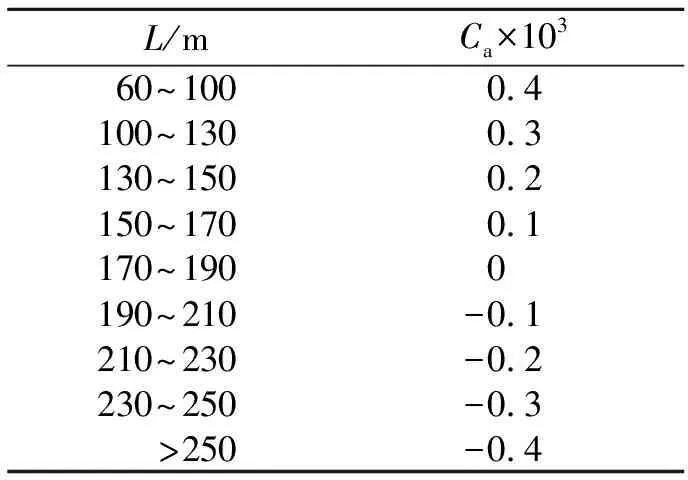
表7 桑海公式Ca值

现分别用不同的粗糙度补贴系数计算几艘典型船舶的摩擦阻力值，并求出摩擦阻力占总阻力的比例见表8～11。其中：Rt为实船总阻力;Rf1，Rf2分别为用荷兰水池和日本船舶研究所计算粗糙度补贴系数方法所得到的摩擦阻力。

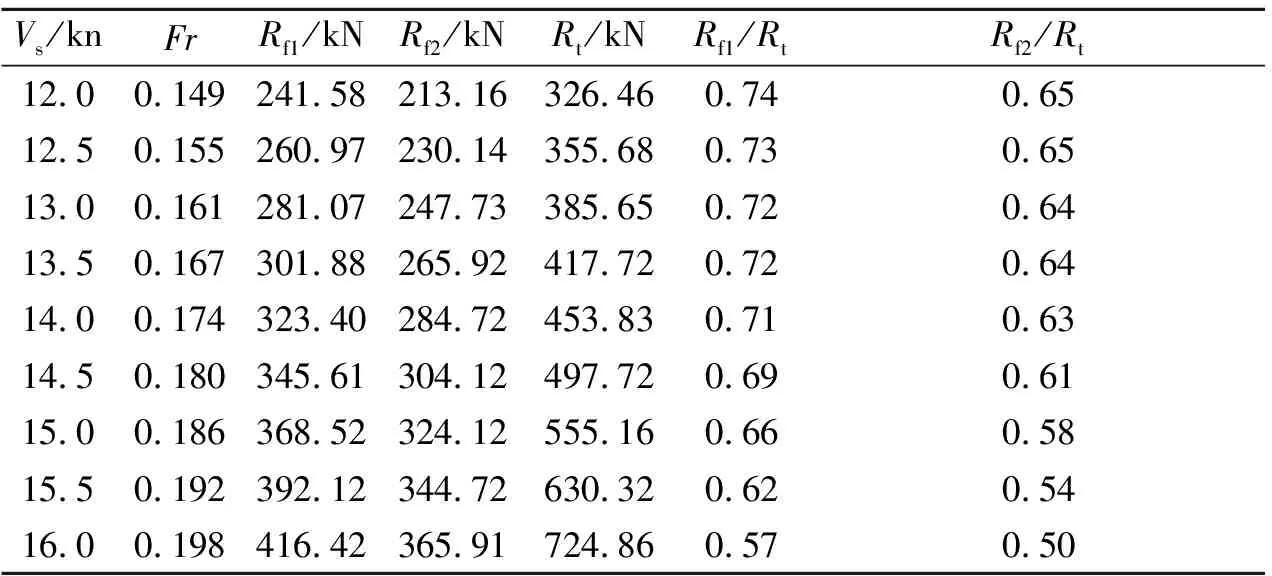
表8 35 000 t散货船摩擦阻力计算

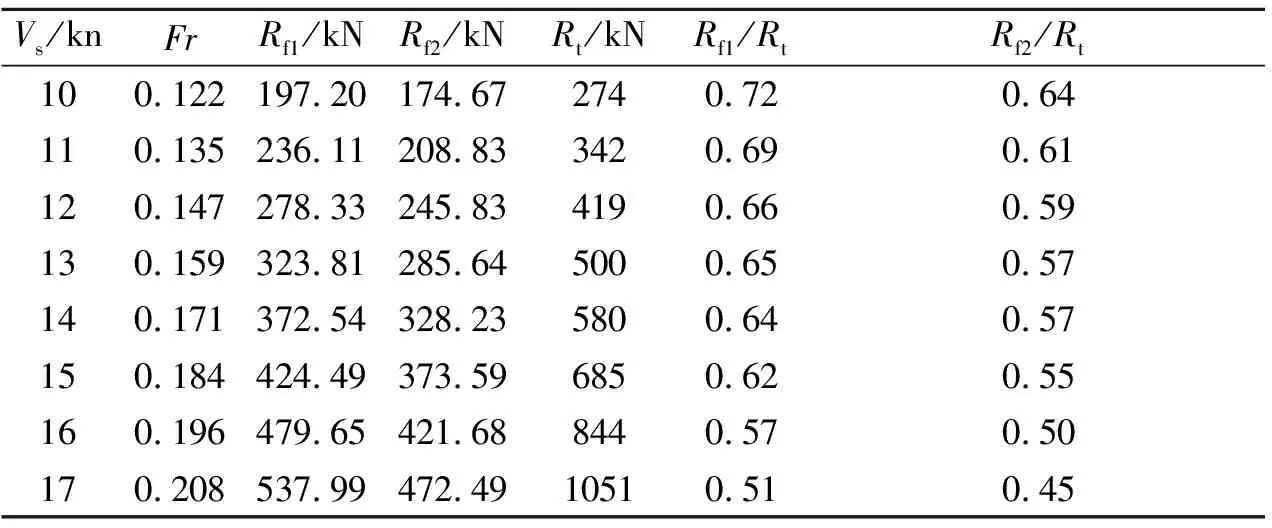
表9 48 000 t油船摩擦阻力计算

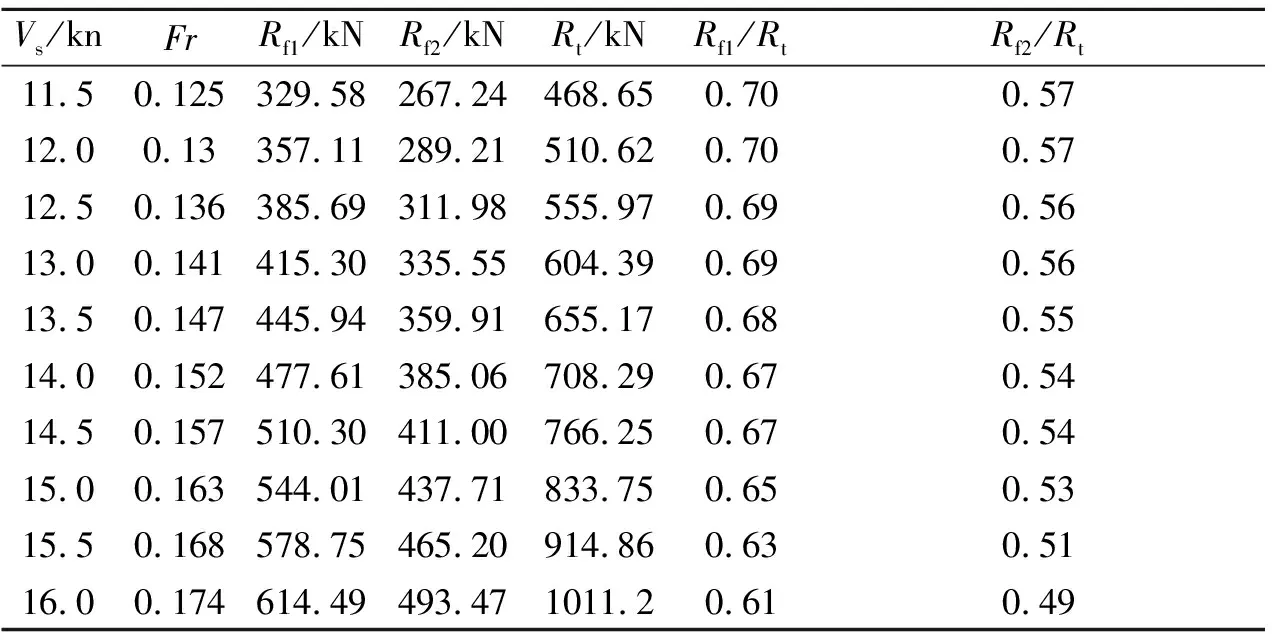
表10 82 000 t散货船摩擦阻力计算

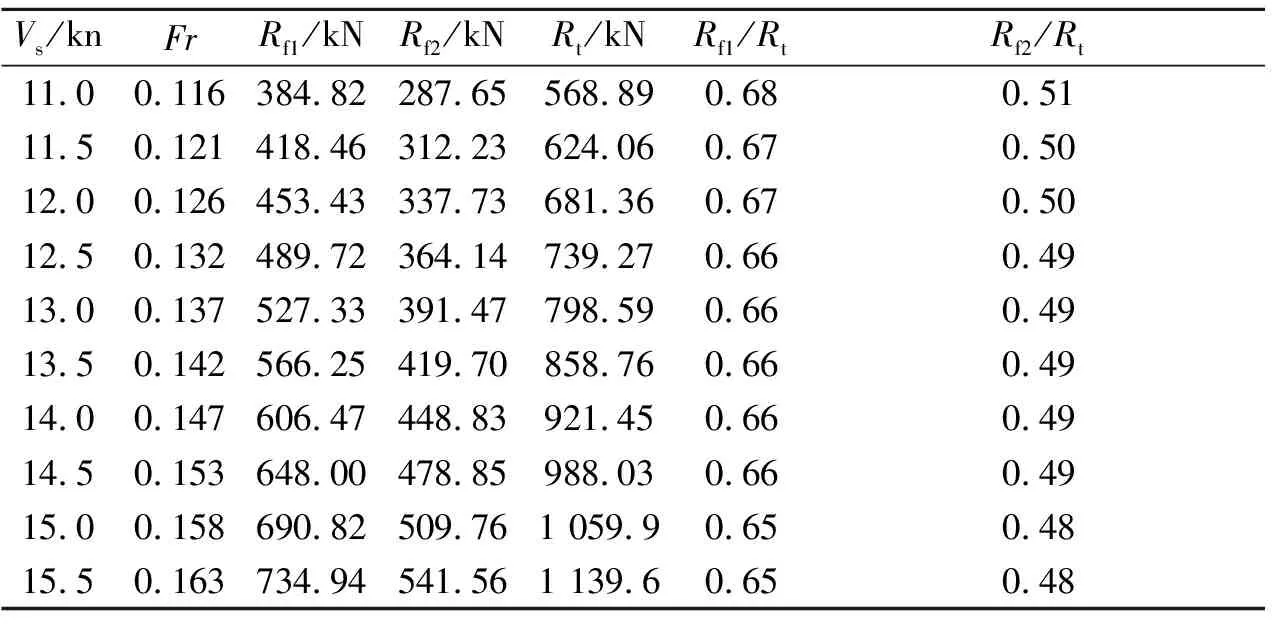
表11 115 000 t油船摩擦阻力计算

按照弗劳德假定的分类方法，两种阻力成分在总阻力中所占的比重随不同航速而不同，对于低速船(Fr<0.20)来说，摩擦阻力占总阻力比例可达到70%～80%。

由表8～11可见，采用桑海公式计算摩擦阻力时，其占总阻力的比例为45%～65%；采用荷兰水池的粗糙度补贴系数方法计算摩擦阻力时，其占总阻力的比例为51%～75%，较之于日本船舶研究所结果更合理。

2.2 剩余阻力计算分析

凯勒对1954年兰坡发表的图谱进行修正和扩充后给出了单螺旋桨民用船估算阻力的图谱，该图谱是根据荷兰瓦根宁船模水池所做的107艘单螺旋桨大型船舶的模型试验结果分析整理而给出的。计算结果见表12～15。表中Cr为剩余阻力系数;Cr×S/AM表示兰坡凯勒图谱中的纵坐标值。考虑到目前的新造船型已经在水动力方面进行过优化和提高，其主要是通过安装球鼻艏和改变艉部型线改变了船舶的兴波阻力，其对摩擦阻力影响不大，但是对剩余阻力有较大的影响，因此，引入与船型参数有关的剩余阻力修正因子α,对剩余阻力部分进行修正。各工况下修正因子α的计算结果见表12～15。

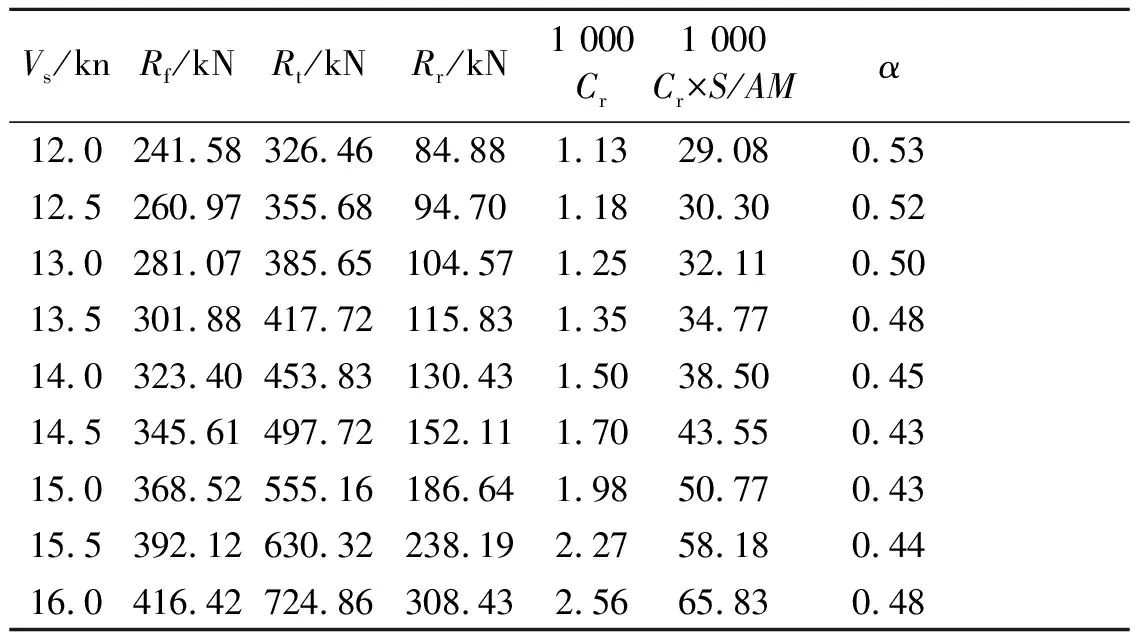
表12 35 000 t散货船剩余阻力修正因子计算

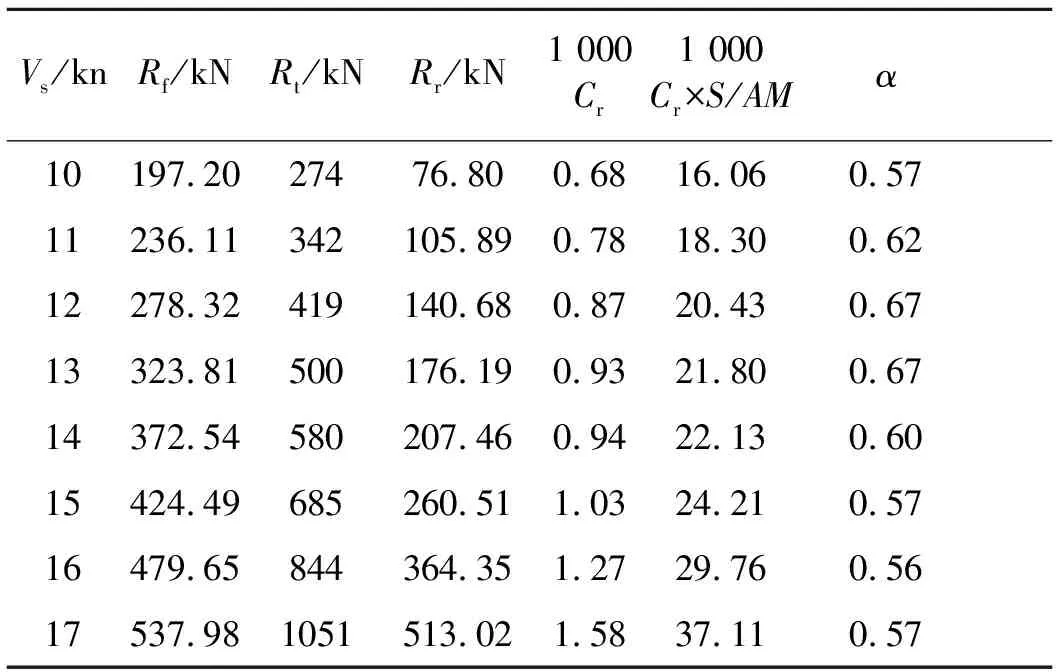
表13 48 000 t油船剩余阻力修正因子计算

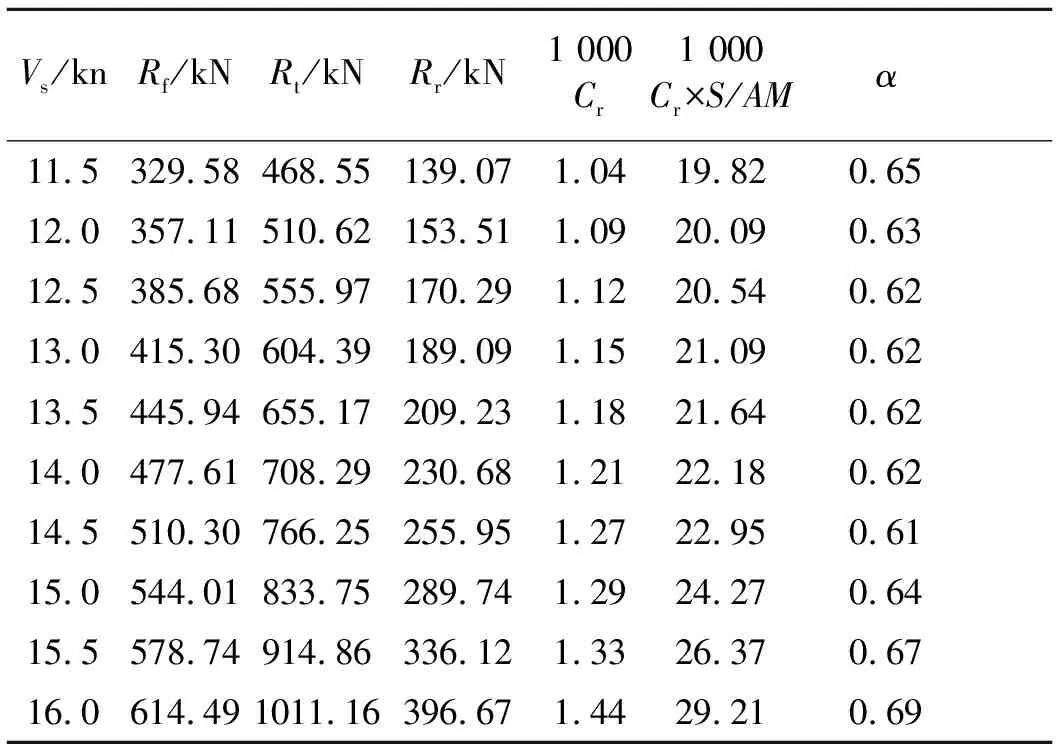
表14 82 000 t散货船剩余阻力修正因子计算

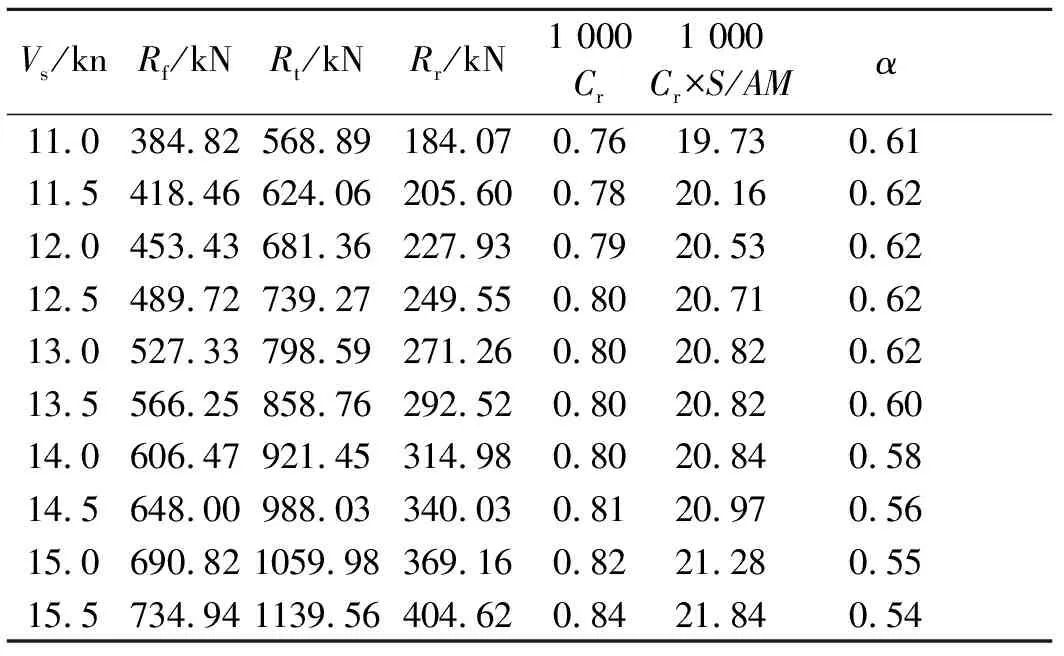
表15 115 000 t油船剩余阻力修正因子计算

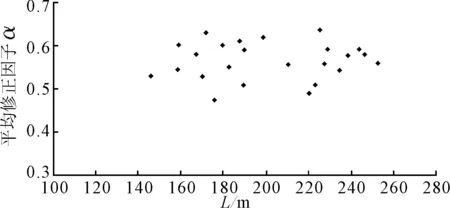
图1 剩余阻力修正因子α随船长L变化

由表12～15的阻力计算结果可知，在设计吃水状态，剩余阻力修正因子α随着船长L在0.50～0.63之间变化。图1为修正后的阻力预报方法与对应几艘单桨肥大船舶水池试验数据换算得到阻力值在航速11～17 kn范围内的修正因子α，其均方差在10%之内。

3 船模水池试验与修正因子函数拟合

3.1 船模试验

船模水池试验是研究船舶阻力最常用的方法，哈尔滨工程大学船模水池是国际拖曳水池(ITTC)成员，水池长180 m、宽7 m、水深3.5 m。图2是35 000 t散货船船模试验示意图，模型主尺度为垂线间长5.891 m，船宽1.027 m,设计吃水状态下艏艉均为吃水0.325 4 m。

图2 船模试验模型安装与试验

3.2 修正因子函数拟合

根据剩余阻力修正因子随船长的分布的关系，对剩余阻力修正因子用MATLAP进行函数关系式的拟合。设计吃水状态下剩余阻力修正因子α与船长的分布见表16。

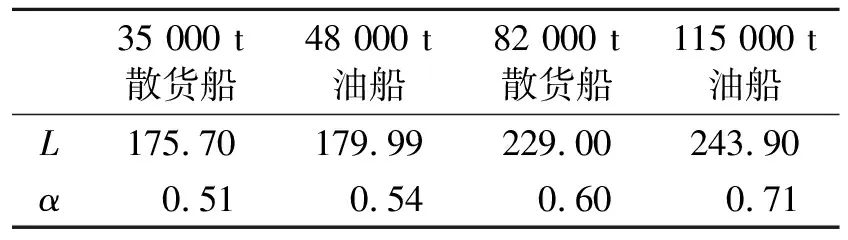
表16 修正因子α随船长变化值

根据MATLAB对剩余阻力修正因子α散点图做函数拟合，可得到设计吃水状态剩余阻力修正因子

α=A1sin (B1L+C1)+A2sin (B2L+C2)

(3)

式中：L为船长;

A1=0.674;B1=0.024;C1=2.559;

A2=0.164 4;B2=0.092 54;C2=-2.719。

根据传统船舶阻力计算方法得到剩余阻力值，与试验值对比发现误差，剩余阻力修正因子α是在分析误差产生的原因和试验值的基础上实现对剩余阻力部分的修正，修正后的剩余阻力加上摩擦阻力部分就可以得到船舶总阻力值。

4 船舶阻力修正方法的验证

为了进一步验证船舶剩余阻力修正因子α的精度和计算方法的一般性，以由渤海船舶重工委托哈尔滨工程大学开发75 000 t散货船试验项目为例，其船型主要参数为

垂线间长Lpp=217.0 m；水线间长Lwl=220.5 m；船宽B= 32.26 m；吃水T=12.5 m；菱形系数Cp= 0.85；方形系数Cb=0.847；浮心纵向位置XB=+0.141。

用修正后的计算方法与试验值进行对比(见表1)，通过式(3)计算得出剩余阻力修正因子α=0.523 0。

由表17可见，修正前误差为25%～30%，而修正后的阻力误差在10%之内，误差明显减小，达到了一定的修正效果。

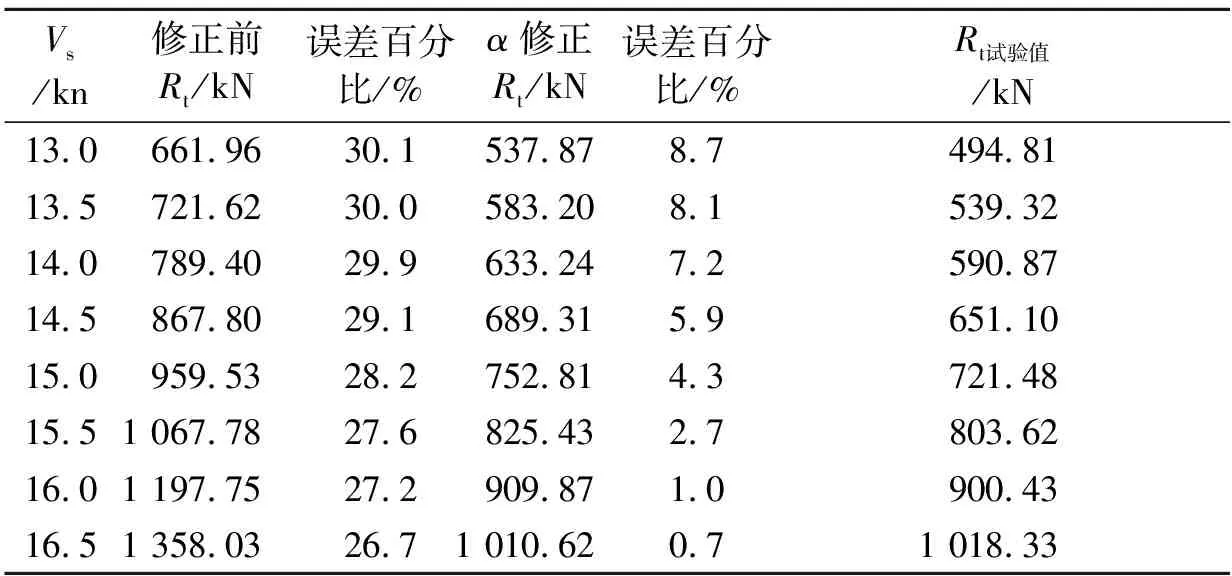
表17 75 000 t散货船阻力计算值和试验值对比

5 结论

1)用传统阻力计算方法计算新造肥大型船舶阻力值并与试验值进行对比，可以看出传统计算船舶阻力的方法误差为20%～40%，已经不适用于新造船舶的阻力计算。而引入剩余阻力修正因子α后，其计算船舶阻力值误差在2%～10%之间，精度明显提高，满足工程上的应用。

2)通过对肥大型船舶阻力成分的分析，可以看出船舶摩擦阻力和剩余阻力在总阻力中所占的比重一般为50%～80%，对于低速肥大型船舶摩擦阻力所占比重可达70%～80%，由此表明用桑海公式和荷兰试验水池粗糙度补贴系数计算结果更接近真实值，计算精度较高。

3)本文方法除应用于预报阻力和功率外，还可以用于主尺度论证，主机功率选择，螺旋桨匹配等工作，能够为新造船型的设计和旧船的快速性能评估提供依据，为国际海事组织出台的EEDI指数的衡量提供参考，为新船型的开发提供指导。

4)通过对系列船模试验数据的分析，本文计算船舶阻力方法使用方便，实用性强。在给定船舶主尺度后，可迅速给出该船的阻力值和功率值。由于样本容量有限，缺少更多的船型参数和试验数据，对于规律研究有着一定缺陷。本文的工作尚需进一步完善，例如不适合细长型高速船舶阻力预报等。

[1] 盛振邦.船舶原理[M].上册.上海：上海交通大学出版社,2004.

[2] 周占群,谢克振,胡 平,等.大型油船航速估算方法[J].中国造船,2010,51(4):36-44.

[3] 张宝吉.低速肥大成品油船阻力估算方法研究[J].造船技术,2010,30(02):20-22.

[4] 李同山,洪碧光,孙洪波,等.船舶剩余阻力系数计算平台的实现[J]大连海事大学学报,2007,33(1):25-28.

[5] 鲍 毅,许定生.船舶阻力的相关系数及其应用[J].船舶工程,2010(6):27-31.

[6] 王金宝，钱文豪.低速肥大船舶阻力成分分析[J].船舶工程,1998(6)11-14.

[7] 李立人.单桨浅吃水肥大船系列实验图谱[J].中国造船,1996(1)1-10.