风载荷下的大型远洋船舶风帆结构静力学仿真

， ,，

(1.武汉理工大学 能源与动力工程学院 可靠性工程研究所，武汉 430063；2.中国中铁大桥局集团有限公司,武汉 430050;3.武汉理工大学 交通学院，武汉 430063)

为推动风帆助航技术的发展，很多国家进行了大量的研究工作并取得了很多成果。

德国的“E-Ship 1”号船。该船布置了4个Flettner型转筒帆，其中两个布置于桥楼后方，另两个布置于船尾处，该船上的4个Flettner型转筒帆可为船舶提供足够的动力。

日本东京大学为 “UT Wind Challenger”号散货船设计桅杆及相配套的刚性风帆，其中风帆采用了曲面中空设计方案，每个帆面都配备单独的电机控制系统，可使帆面以最佳的帆角来捕捉风能。

本文根据已有的帆型进行优化得到一种新帆型结构，对新帆型结构用ANSYS软件建立有限元模型，并且对风帆模型在7～10级的风力作用下的静力响应进行仿真。

1 目标船风帆的参数设计

1.1 目标船的选择

本文所研究的目标船为载重量76 000 t巴拿马型“文竹海”号散货船，该船的主要参数见表1。

1.2 所选风帆的基本参数设计

目标船风帆采用层流型矩形硬帆，并采用钢制骨架构建风帆[1]，其展弦比为0.8，拱度比为0.12，考虑到该散货船的航行区域以及风帆性能等自身因素，得出目标船层流型矩形风帆的基本参数，见表2。

表2 风帆基本参数 m

风帆在船上的布置情况见图1。

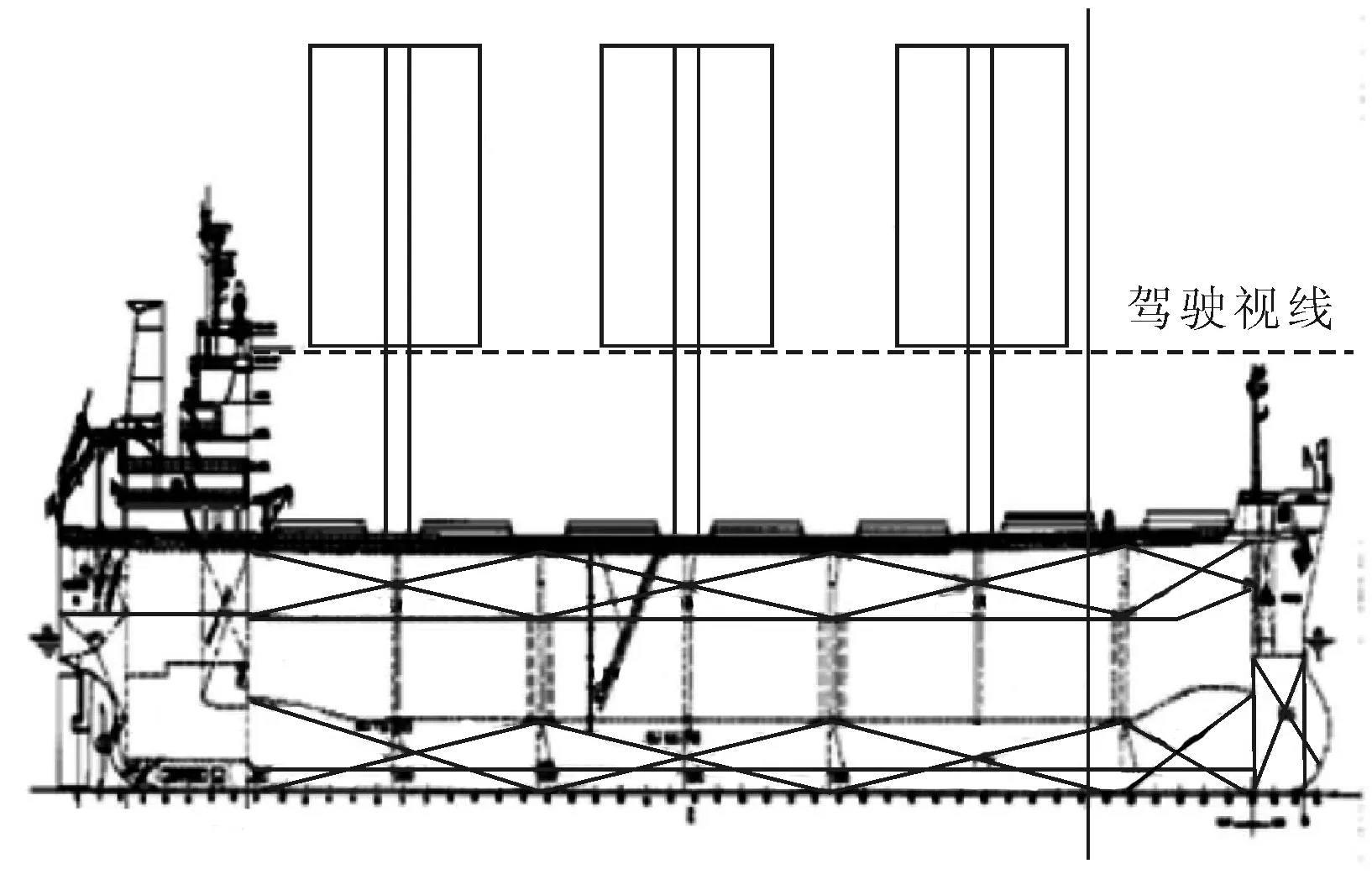
图1 目标船风帆总布置示意

2 风帆结构三维模型的建立

2.1 所选风帆的基本结构设计

风帆结构的材料由船用AH36钢和超高分子量聚乙烯合成纤维组成，其中超高分子量聚乙烯纤维(UHMW-PE)是目前众多合成纤维中强度非常高的纤维之一，具有高强度、高模量、低密度、低吸湿率等一系列优点，强度相当于普通钢材的15倍，模量仅次于碳纤维，密度小于水，纤维吸湿率为零。所选材料的基本参数如表3。

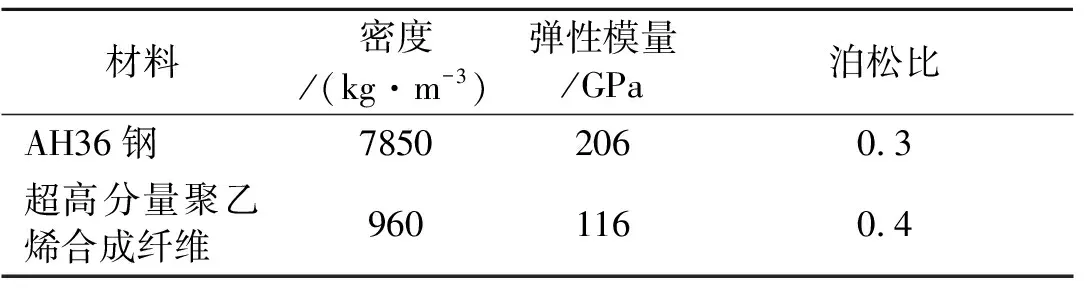
表3 材料的基本参数 m

帆面的主梁(帆面骨架)以及帆用桅杆均采用AH36钢来搭建。为了便于风帆自动控制技术的实现，风帆的开启和关闭采用了液压传动控制技术。通过液压杆的伸长来撑开整个帆面，即开启帆面；通过用液压杆的收缩使得整个帆面闭合，即收拢帆面。风帆的基本结构设计见图2。

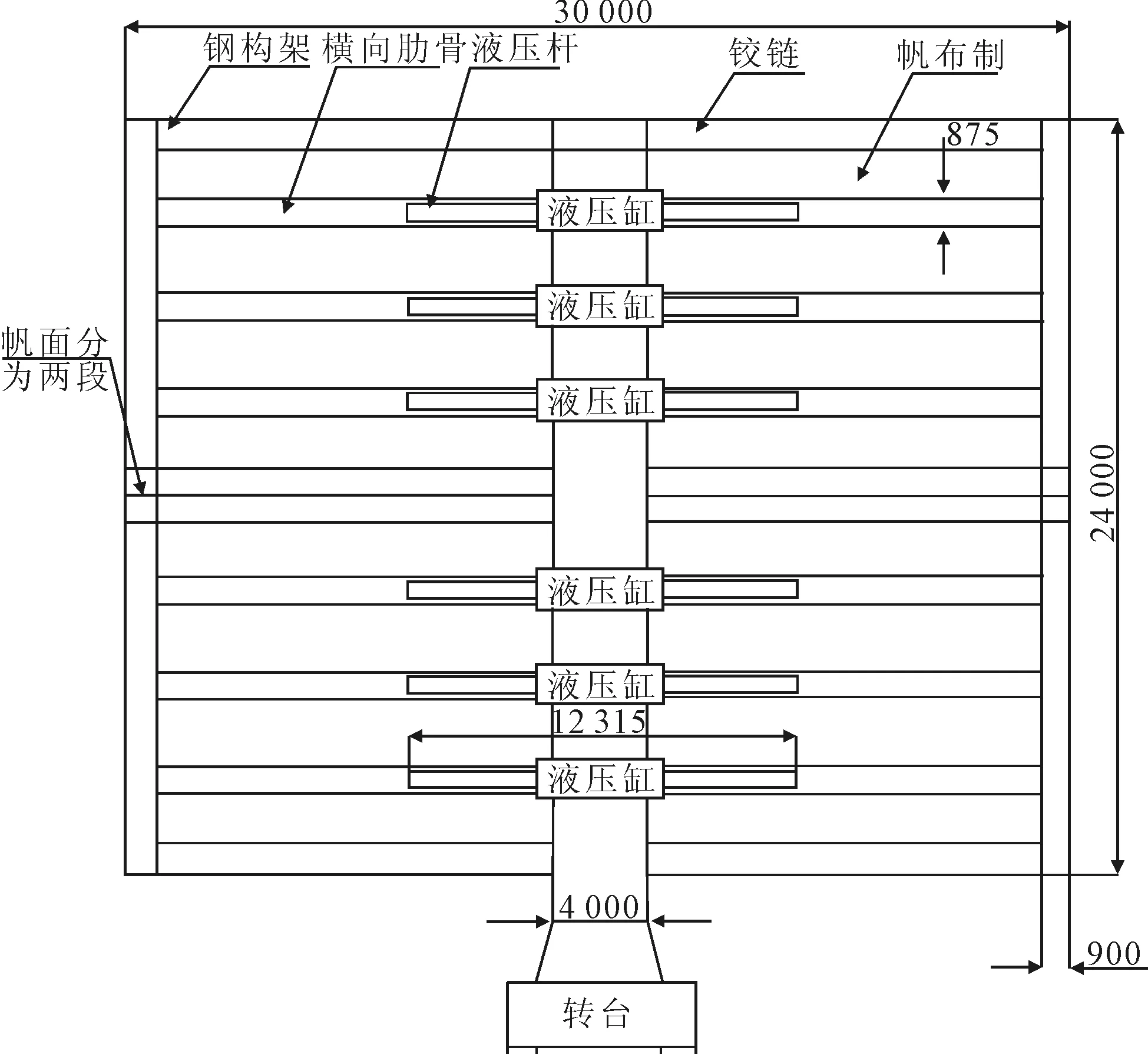
图2 风帆基本结构示意

2.2 风帆结构的三维模型

图3 风帆结构的三维模型

在确保风帆结构强度的基础之上，为进一步减轻风帆整体结构的重量，帆面将采用超高分子量聚乙烯合成纤维来制作双层中空帆面[2]。双层中空帆面结构的空气动力学特性与飞机机翼相似。钢与纤维材料之间通过铆钉链接在一起。风帆结构的三维模型见图3。

3 风帆有限元模型的建立及网格划分

3.1 约束条件

风帆模型的桅杆底部采取固定约束，并在风帆的正迎风面施加与航向相反的风载荷，由于前期对于相关航道上风速，风向等数据的缺乏，在不能准确做出动态分析的情况下，首先以静态分析为主，为后面的动态分析打基础。

3.2 载荷加载

为了更真实地模拟风帆受到风载荷作用的情况，通常选取风帆受力的极限位置作为研究对象。根据空气动力学原理的相关理论，风压与风速间的关系可表述为

p=0.5·ρ·u2·Cp

(1)

式中：ρ——空气密度，1.25 kg/m3(标准状态下)；

u——受风中心风速；

Cp——受风体的空气动力特性系数，按相关资料取Cp=1.2。

p=0.75u2

(2)

利用式(2)可将不同风速等效转换为作用在风帆上的风压，表4为7～10级风速及相应的风压值。

表4 风速等级和风压

3.3 有限元单元的选择

风帆模型主要由薄壁(30 mm)结构构成，因而在有限元分析时就要选取合适的单元类型。本文所研究的风帆模型属于结构分析的范畴，风帆模型的结构均可视为薄壁结构，因此用壳单元来分析风帆模型是合适的[3-5]。

在风载荷确定之后，本文选用的壳单元是SHELL63单元。SHELL63单元既具有弯曲和薄膜特性，也可以承受平面内荷载和法向荷载，该单元的每个节点都具有6个自由度，即：沿节点坐标系X、Y、Z三个方向的平动和沿节点坐标系X、Y、Z三个轴方向的转动[6]，能够满足本文的需求。

3.4 网格的划分

由于选择了SHELL63单元，实际上也就是将体划分转变为面域的划分问题，并且采用面域划分中的自由划分[7]。就本论文而言，整个风帆结构均都选用壳单元SHELL63，得到风帆有限元结构模型见图4，局部网格划分见图5。

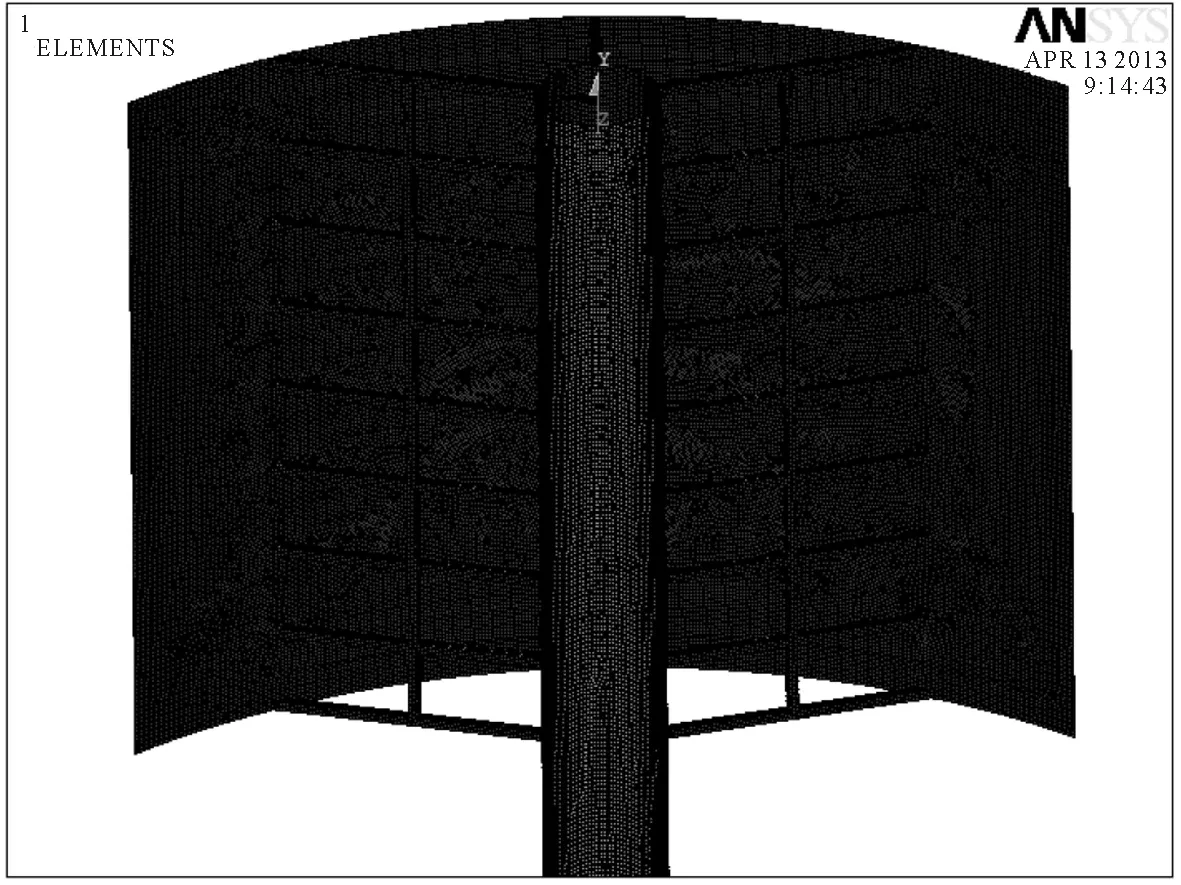
图4 风帆的有限元结构模型

图5 风帆结构局部网格放大

4 风帆在风载荷作用下的静力学分析

4.1 风帆结构在7～10级风载荷下的静力学分析

由表4可见，按照风等级的相关特性，可将风速等效为风载荷(风压)。由于风帆在风场中既受到了不同等级风载荷作用，同时也受到了自身重力的作用(自身重力不可忽略)，考虑风帆同时承受风载荷和重力载荷作用，进行风帆结构的静力学分析。

1)7级风载荷和重力共同作用下的静力学分析。可以较为直观地获知风帆最大的变形量为58 mm，最大变形截面发生在帆面的两侧边缘。桅杆的最大变形量均在40 mm以内。同时可以得到风帆等效应力的分布，帆面和桅杆的应力分布绝大部分都低于90 MPa，在风帆连接杆与桅杆的连接处产生了局部的应力集中，其最大应力为133 MPa。结果见图6和图7。

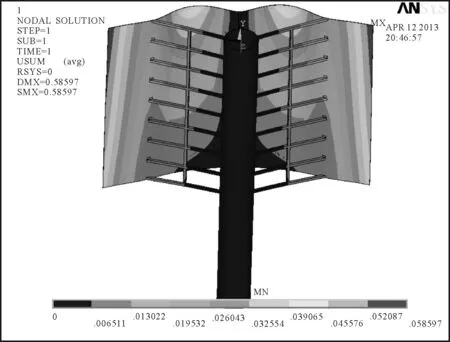
图6 7级风速下风帆的位移云图

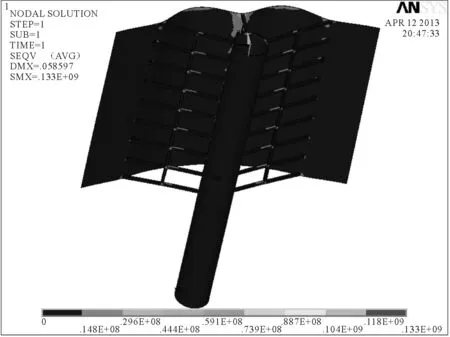
图7 7级风速下风帆的等效应力分布云图

2)8级风载荷和重力共同作用下的静力学分析。可以得到风帆在8级风作用下的位移情况，风帆的最大变形量为87 mm，最大变形截面发生在帆面的两侧边缘处。帆面的变形较大，桅杆和连接杆的变形均控制在65 mm以内。同时得到风帆的等效应力分布，风帆的平均应力分布较为合理，帆面和桅杆的应力分布绝大部分都低于90 MPa，在连接杆与桅杆的连接处产生了局部的应力集中，最大应力为134 MPa。见图8和图9。

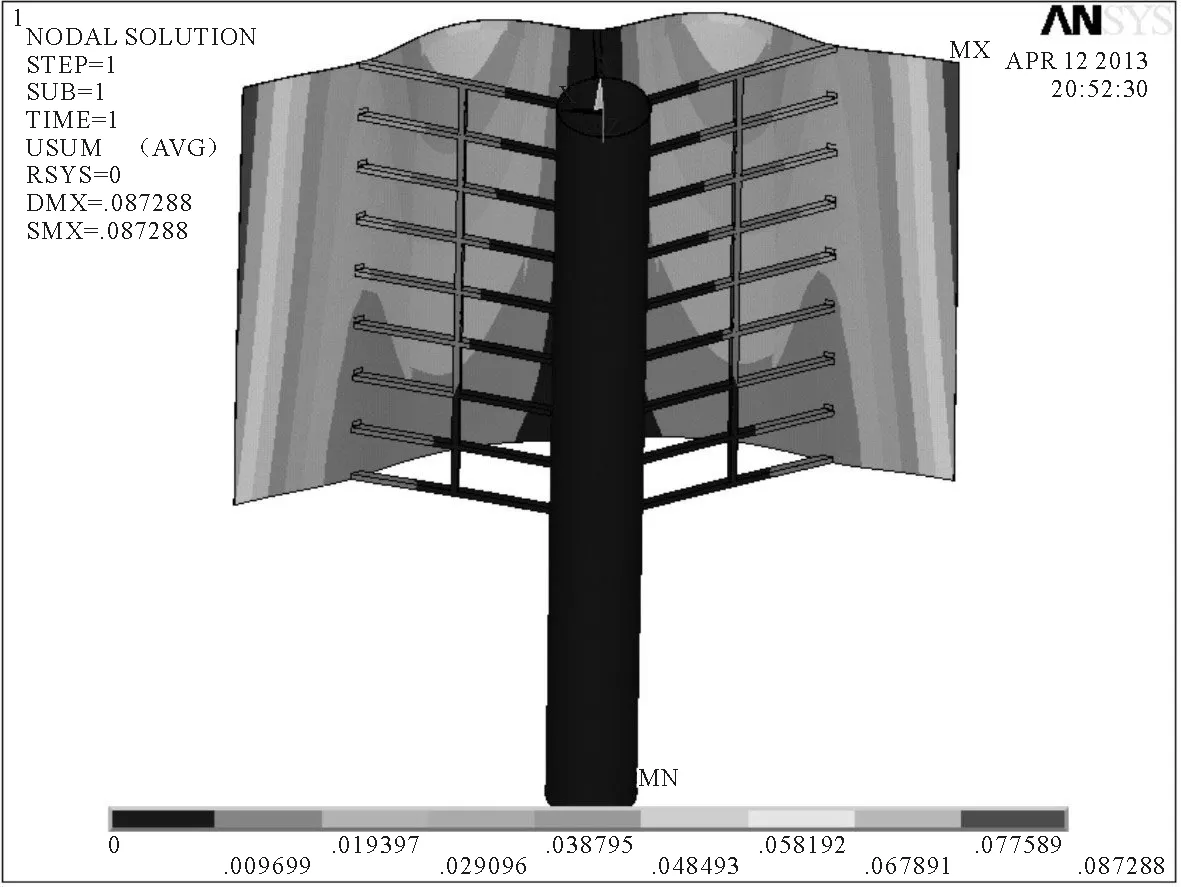
图8 8级风速下风帆的位移云图

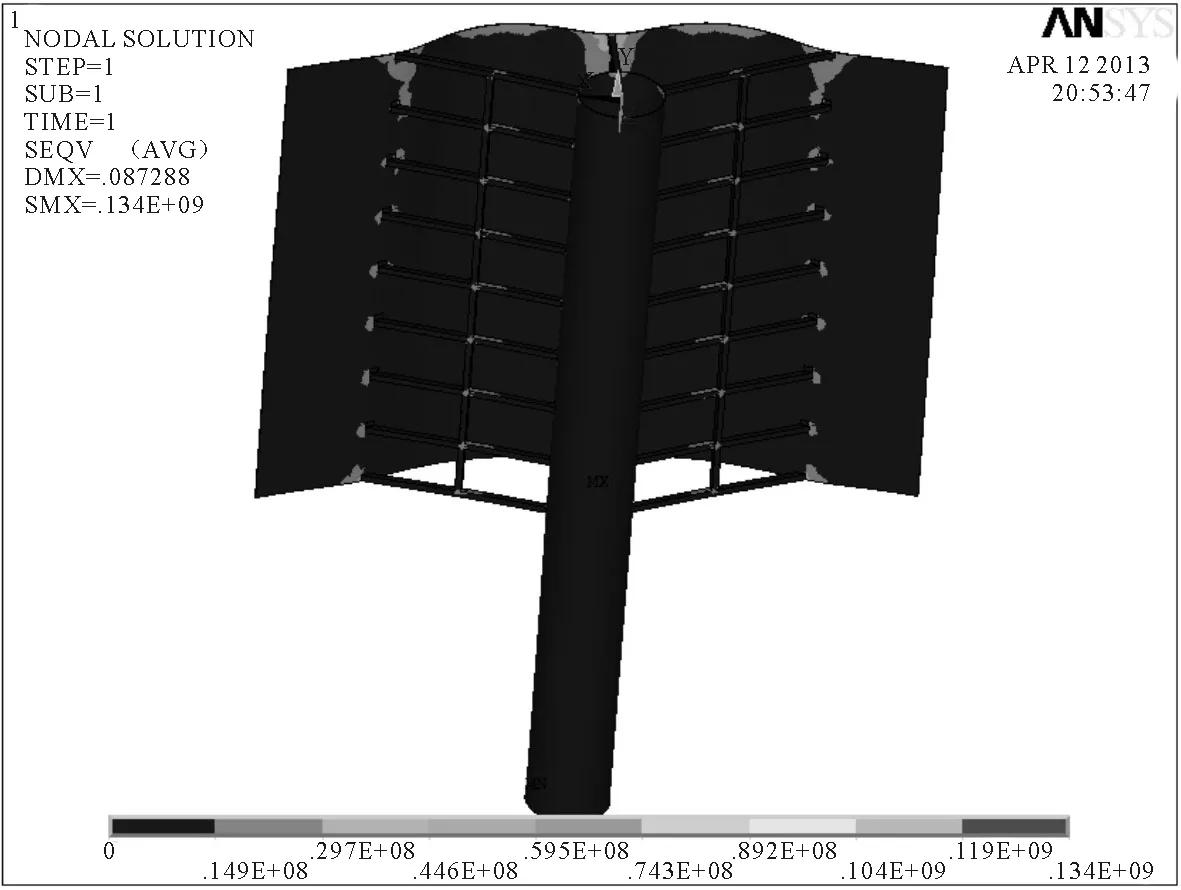
图9 8级风速下风帆的等效应力分布云图

3)9级风载荷和重力共同作用下的静力学分析。可得知风帆的最大变形量为118 mm，最大变形截面发生在帆面的两侧边缘。帆面与桅杆的大部分变形量均控制在85 mm以内。其中钢结构材料的变形量在85 mm以内。同时得知风帆在9级风载荷作用下的平均应力分布情况，风帆上平均应力分布较为合理，帆面和桅杆的应力分布大部分都低于100 MPa，而在连接杆与桅杆的铰接处产生了局部的应力集中，其最大应力为153 MPa。见图10和图11。

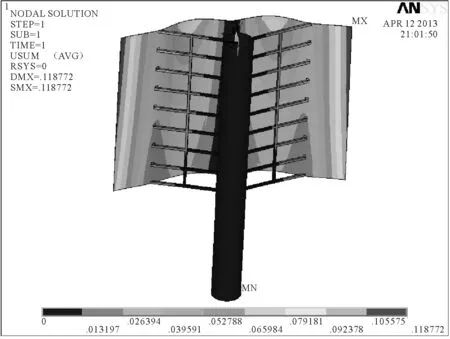
图10 9级风速下风帆的位移云图

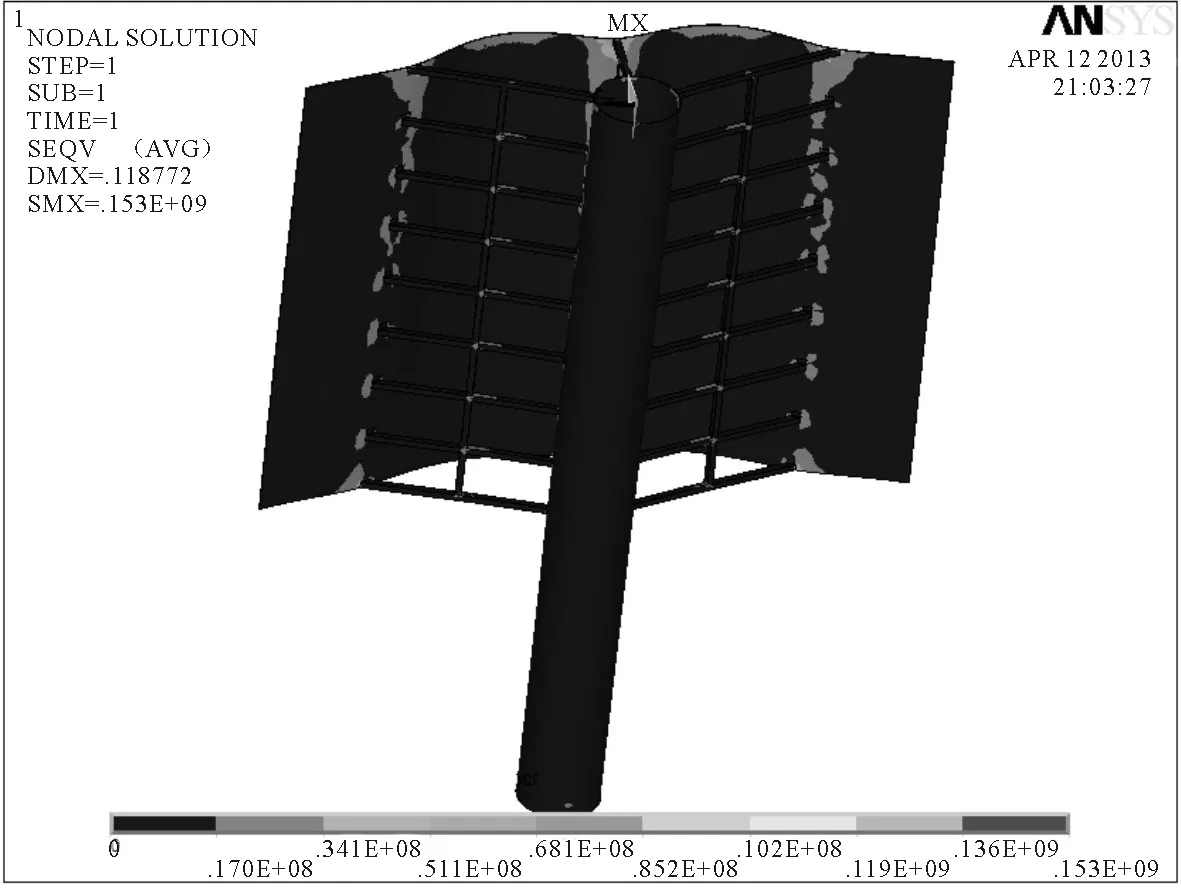
图11 9级风速下风帆的等效应力分布云图

4)10级风载荷和重力共同作用下的静力学分析。可以获知，风帆的最大变形量为160 mm，变形的最大位置发生在帆面的两边缘位置，钢结构材料变形量控制在110 mm以内。同时得到风帆在10级风载荷作用下的平均应力分布情况，帆面和桅杆的应力分布大部分控制在132 MPa以内，在风帆连接杆与桅杆的连接处产生了局部的应力集中，其最大应力为193 MPa。见图12和图13。

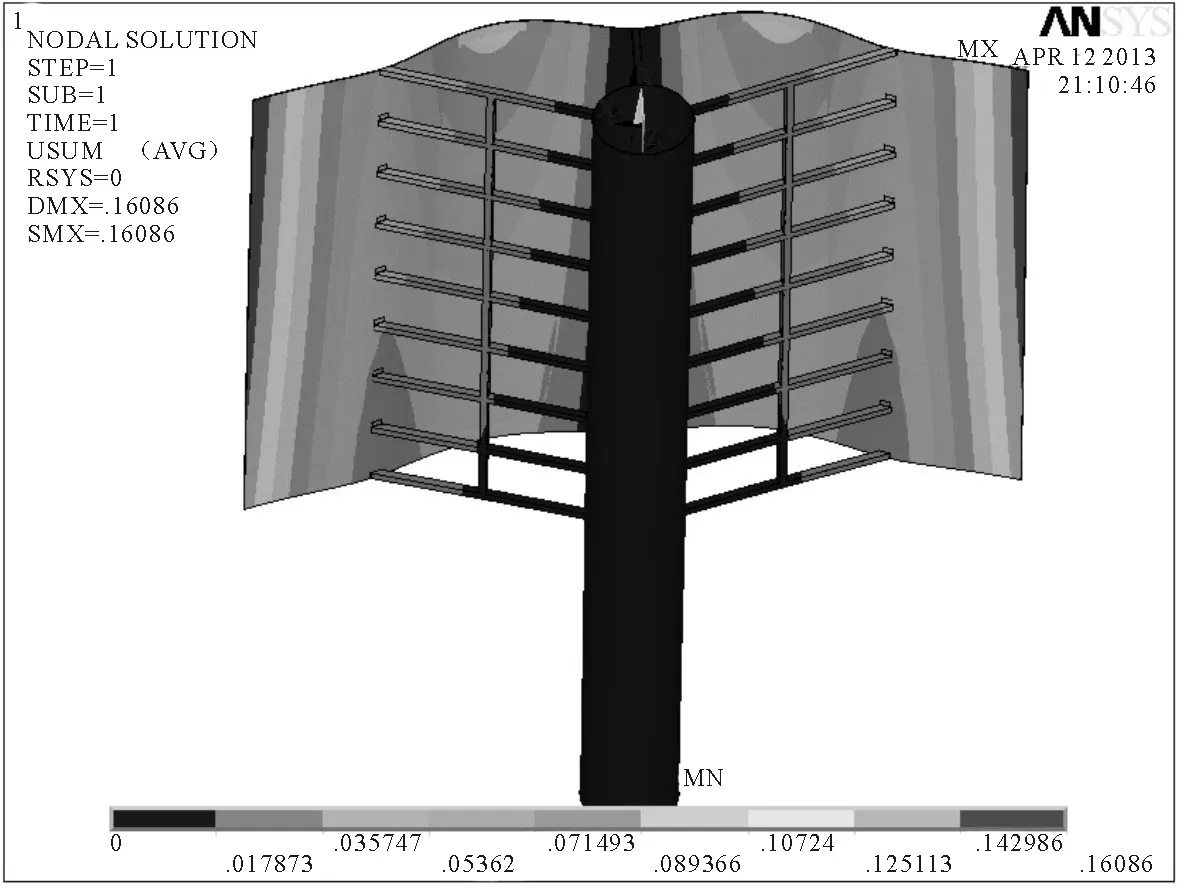
图12 10级风速下风帆的位移云图

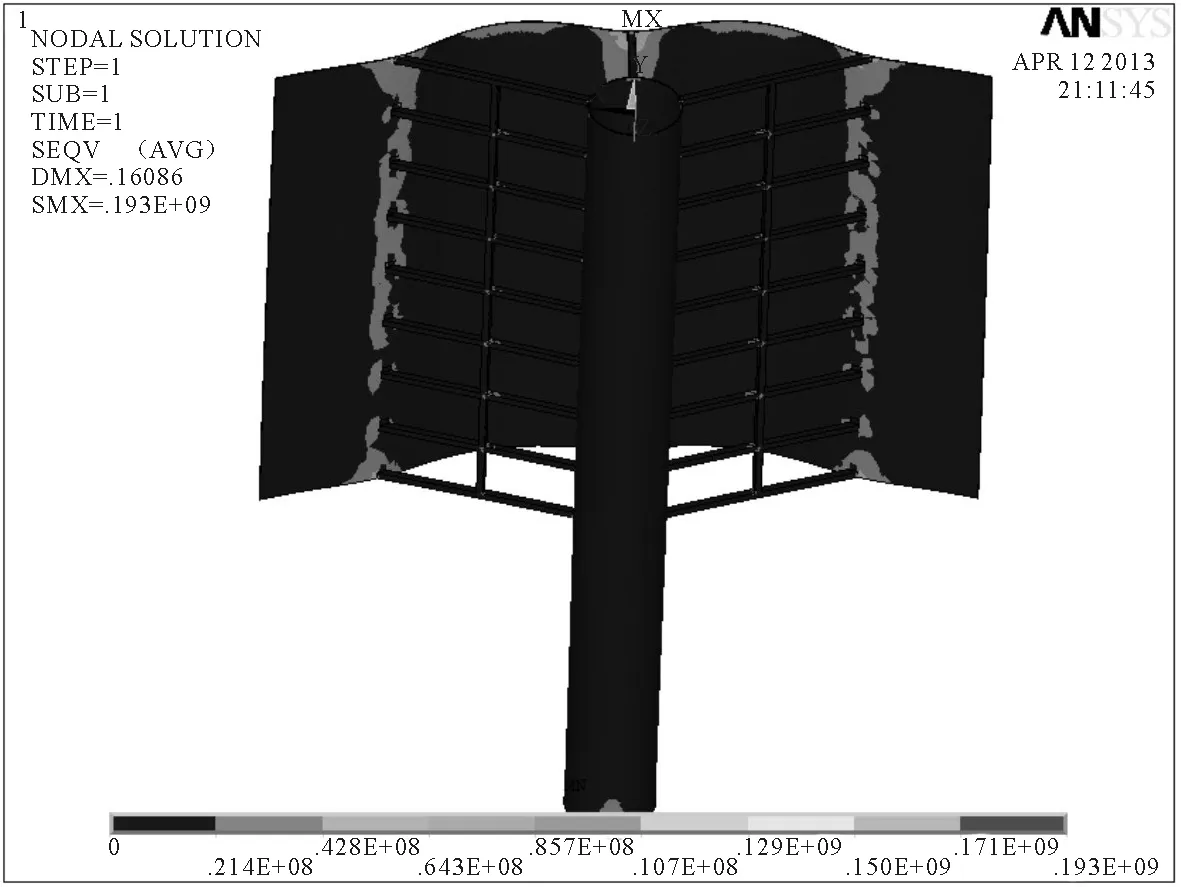
图13 10级风速下风帆的等效应力分布云图

4.2 综合分析

通过对风帆在不同风载荷和重力载荷共同作用下的仿真计算，可从仿真结果的云图中获取风帆各部件的受力及变形值，对计算结果做简要整理与分析，结果见表5。

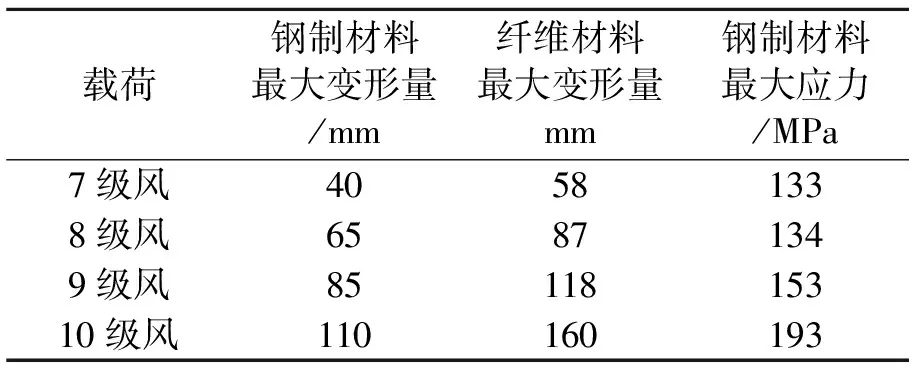
表5 风帆计算数据结果汇总

本文风帆设计主梁(帆面骨架)以及帆用桅杆均采用AH36船用钢板，依据国家标准GB150—1998常规设计中关于A系列材料的选取准则，钢材屈服极限σs=355 MPa，Ns=1.5，安全系数选取标准见表6。

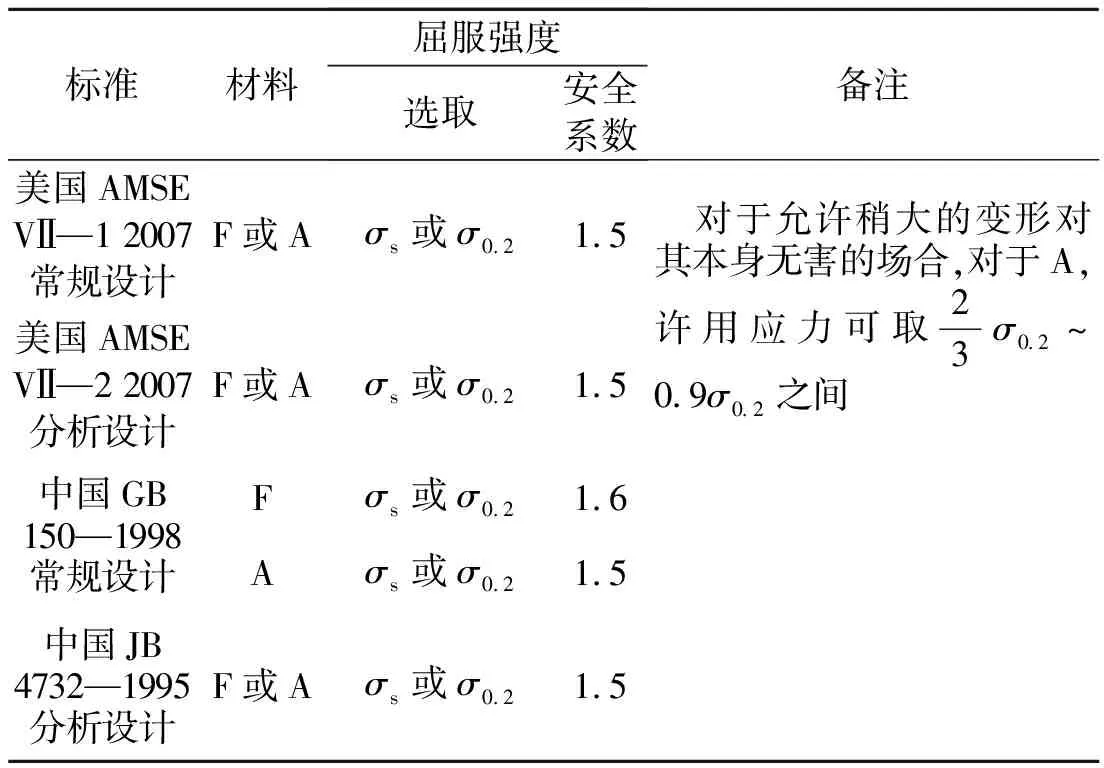
表6 安全系数选取标准

(3)

通过对比分析可知，当σmax≤[σ]时，设计的风帆结构能够满足风载荷的冲击作用，即10级及以下风载荷下的风帆的整体强度和形变量都能满足材料的相关要求。

5 结论

在确定材料安全系数Ns=1.5的情况下，风帆结构能够承受10级及以下风载荷的作用。当风帆结构在某一级风情况下发生结构安全性无法满足要求时，就需要以此风级为限度，控制风帆的使用，必要时及时收帆。

考虑到目标船的航行区域，仿真结果表明新的风帆结构及强度基本满足设计要求，可为设计提供数据及理论支持。

今后的工作中可以进一步完善风帆的结构设计，可对风帆的结构做进一步优化，具体如下。

1)增加帆面与桅杆之间连接杆的数目，即减少每两连接杆之间的间距。

2)在连接杆之间增加纵向连接构件，增加连接机构的整体刚度。

3)改善应力集中处材料的表面属性和接触面的材料属性。

[1] LUYU C,SHUNHUAI C,YIGONG W.Analysis on sail selection and energy conservation of a Panamax bulk carrier[C]∥Advances in Energy Engineering (ICAEE),2010 International Conference on.IEEE,2010:182-185.

[2] 甘振海.风筝帆助航技术研究[D].大连：大连海事大学。2009.

[3] 江国和,周中良,胡以怀,等.基于ANSYS的船用风帆结构强度有限元模型分析[J].造船技术,2011(2)：10-12.

[4] 张学宁.“明州22”号船风帆骨架强度有限元分析[J].船舶工程,1996(4)：14-16.

[5] 王新敏.ANSYS工程结构数值分析[M].北京：人民交通出版社,2007.

[6] 胡仁喜,徐东升,李亚东.ANSYS13.0机械与结构有限元分析[M].北京：机械工业出版社,2011.

[7] 李黎明.ANSYS有限元分析实用教程[M].北京：清华大学出版社,2005.