中间热交换器建模仿真研究

张厚明，段天英，王 刚，刘 勇，熊文彬，刘兆阳

（1．国家核安全局华北核与辐射安全监督站，北京100191；2．中国原子能科学研究院，北京102413；3．国家核安全局核与辐射安全中心，北京100082）

中间热交换器是液态金属冷却快中子增殖堆（以下简称“快堆”）热传输系统中隔离放射性的一回路载热剂与非放射性二回路载热剂的屏障，同时也是将堆芯释热传递给蒸汽发生器的重要设备。

对于快堆核电厂热工水力、仪控系统的设计来讲，中间热交换器的建模及仿真研究可以为之提供设计依据。同时，可以将建模及仿真研究的成果用于设计工程仿真机、全范围仿真机来为操作员提供培训。另外，仿真模型在高速计算机上运行，通过实时采集快堆核电厂数据提前计算出各个参数的运行趋势，从而为操纵员提供技术支持。因此，对于上述三个方面，中间热交换器建模及仿真研究都具有重要意义。本文给出一种计算迅速、精度较高、可以用于控制系统分析、实时计算的中间热交换器仿真模型。

1 中间热交换器建模简介

早期实验、原型快堆中间热交换器类型、结构形式较多［1，2］，例如：BN－350采用竖直U形传热管束置于水平矩形筒体内；BR－5及Grand Quevilly French Test Station采用U形传热管束置于U形筒体内；Fermi及FFTF采用直传热管置于竖直圆柱形筒体内，采用可移动的封头来补偿热膨胀效应；Hallam Nuclear Power Facility采用直传热管，壳侧有膨胀节来补偿热膨胀效应。

示范、商用大型快堆，例如Super Phénix、CRBRP（未建造）、BN－800，均采用直换热管、逆流管壳式中间热交换器。二回路钠均从顶部进入，通过中心下降管流到底部下腔室，然后流向反转，向上流过换热管束。一回路钠均从上部进入，流经传热管间的壳侧，从底部流出，如图1所示［3］。

因此，本文选取某个直换热管、逆流壳式中间热交换器作为研究对象。

描述中间热交换器三维热工水力的方程组非常复杂。由于动量、能量方程的相互耦合，并且，这些方程的非线性使得方程组很难求解。然而，即使在自然循环工况下，三维计算结果与一维计算结果也相差不大［4］，因此以往的研究中，大多假设：

图1 CRBRP中间热交换器概图Fig．1 Sketch of CRBRP IHXs'

（a）用一根传热管代替传热管束；

（b）流体物性参数沿径向保持不变；

（c）忽略载热剂、管壁的轴向导热；

（d）忽略中间热交换器壳体的散热。

在上述这些假设下，Gunby［5］采用“节距固定”方法将中间热交换器的传热管划分为10个等长节段，在每个节段上建立了能量守恒微分方程组，采用不同的差分来求解，研究了流量、入口温度变化等各种工况下中间热交换器的温度的分布及变化。研究结果表明：对一、二回路不平衡流动（10∶1），流量大的一侧其计算结果差别较大；并且，即使出口温度计算结果较为可信，各种差分方法计算出的内部温度分布也均不正确；在要求出口温度和内部温度分布计算结果同时可靠时，大扰动情况下，采用这种“节距固定”的方法，划分节段数目较少时，各种差分方法均难以获得正确的计算结果。

Brukx［6］针对Gunby方法中出现的内部温度分布不正确问题，给出了一种将能量守恒微分方程组在空间上离散的差分计算方法，计算结果较好，但这种方法中无法实时计算温度变化，在控制系统设计，例如使用Matlab／Simulink软件对控制系统进行设计中，诸多不便。

段天英［7，8］根据能量守恒方程，在小扰动情况下推导出中间热交换器出口温度随流量、入口温度等参数变化的传递函数，并将传递函数进行修正，计算结果较为精确，这种方法可以用于扰动不大的控制系统设计中；但是，这种方法无法计算各种瞬态工况下中间热交换器内部的温度变化，且不可以用于扰动较大的控制系统设计。

Tzanos［9］给出两种中间热交换器模型。第一种为“节距固定”方法：将传热管均分为145个节段，在每个节段上采用能量守恒方程进行描述，这样获得描述中间热交换器模型的常微分方程组。由于早期计算机运算速度较慢，Tzanos给出第二种“节距可变”方法：将中间热交换器按照等能量划分为10～15个节段，采用Leibnitz方程将每个节段上的能量守恒方程偏微分方程组转化为温度导数与节段长度导数有关的常微分方程组。由于出口温度变化与长度变化有关，“节距可变”方法使得节段平均温度为节段出入口温度的算术平均值这一假设在节段数目较少的情况下比“节距固定”的方法更为合理，于是，采用这种阶段长度可变的方法可以大大减少常微分方程组维数和计算机机时。但是，这种“节段长度可变”的方法与“节距固定”方法的计算结果仍有一定差别。这种方法在EBR－Ⅱ的TEST－8A试验［9，10］中得到验证，最大计算误差在6K左右。

综上所述，在以往的对中间热交换器建模的各种方法中，采用“节距固定”的方法来建立中间热交换器模型，若取得较好的计算结果，瞬态过程中中间热交换器内温度可信，不会出现数值不稳定，那么节段数目的选取应至少为100个左右［9］。本文给出150节段、适于Matlab／Simulink软件中计算的“节距固定”模型。本模型建立过程中首先提出两种稳态计算方法，比较两种方法计算的稳态结果，然后给出一种瞬态模型，并将稳态计算的结果作为瞬态计算的参数，对二回路钠流量指数衰减的工况进行了计算，以下分别介绍稳态、瞬态计算模型。

2 中间热交换器稳态计算方法

文献［11］在假定稳态情况下整个中间热交换器内钠、换热管材料的比热容及换热系数均不变，推导出沿高度方向温度呈指数分布，这种计算方法较为粗糙，计算结果误差较大。但本文在程序设计中将这种方法计算出的结果作为粗略估计值，从而可以减少稳态计算的循环次数。

本文给出的两种稳态工况下的计算方法，将中间热交换器传热管分为n个节段，如图2所示。

图2 中间热交换器第i个节段Fig．2 Segment i in IHXs

稳态工况下，中间热交换器在节段i上的能量守恒方程为：

式（1）中，

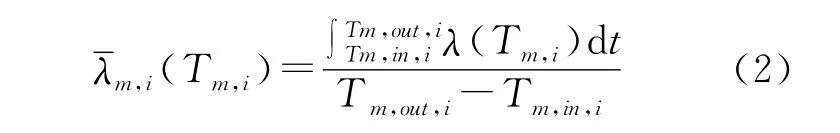
其中，W为质量流量，C为比热容，U为传热系数，l为节段长度，T为温度，λ为热导率，a为一回路流道截面积，p为节距；角标p为一回路，m为管壁，s为二回路，in为管内，out为管外。

根据式（1）采用包括：等节段长度、等换热量两种方法来划分节段数目并编制程序，具体算法、循环语句如图3所示。根据这两种方法，分别调整α、β、δ、ε的值，可以获得精度较高的计算结果，经过计算两种算法出的结果相差很小，如图4所示。与实际值相比，所计算出的值绝对误差误差在3K以内。

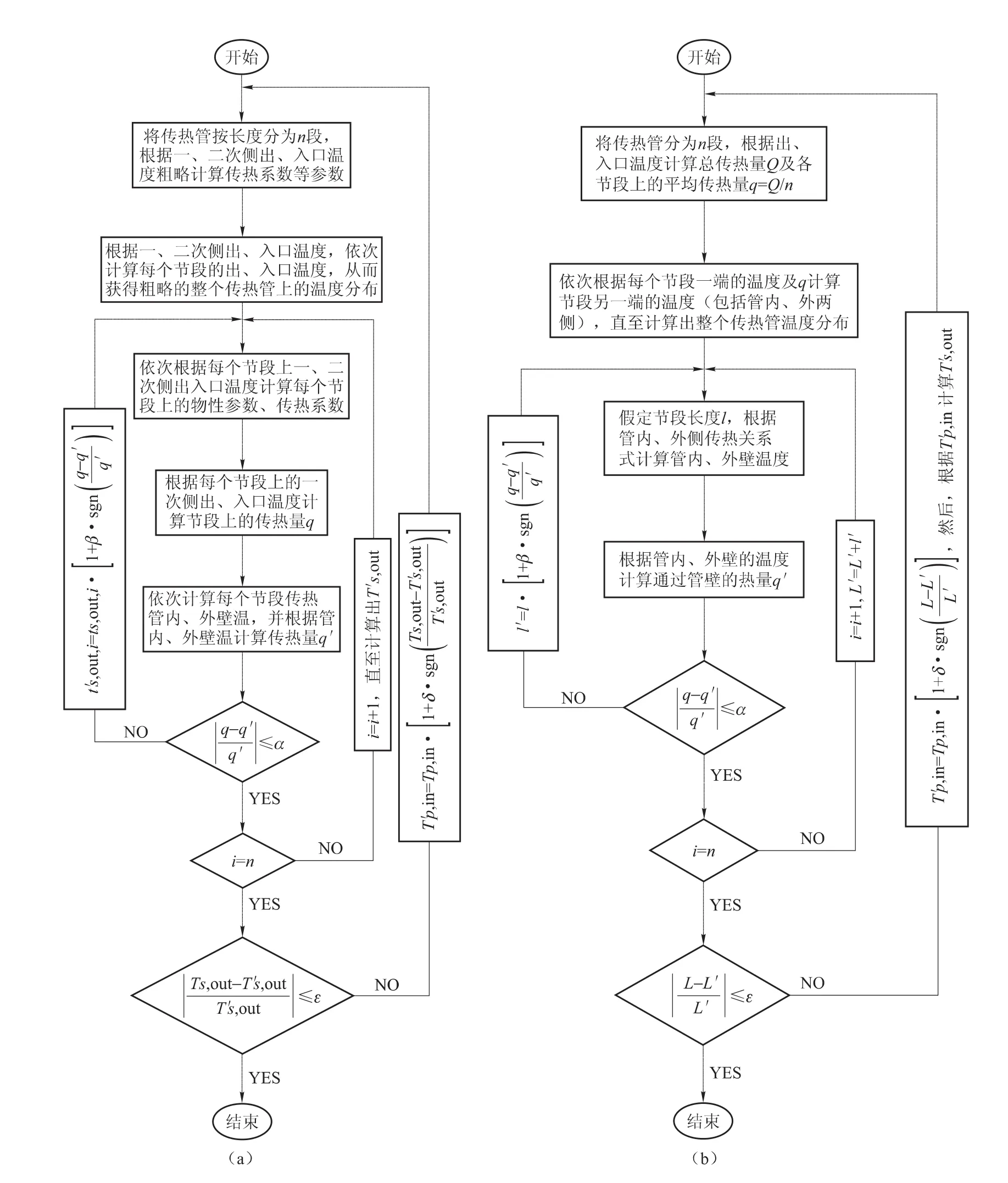
图3 稳态计算方法Fig．3 Steady state algorithms

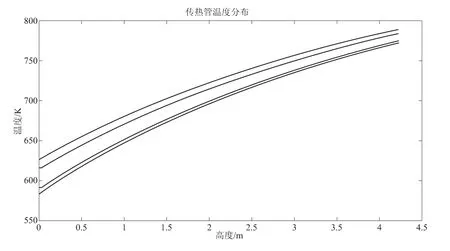
图4 稳态工况下的计算结果Fig．4 Calculated result with steady state algorithms

由计算结果可知：管内热阻不超过总热阻的15%～20%，壳侧的传热系数明显小于管侧，其热阻约为总热阻的30%～40%，管壁热阻约为总热阻的40%～55%。因此在设计中，进一步增加管内流速不会大幅降低总热阻；增加壳侧的流速可以有效降低总热阻，减小管壁厚度可以大大降低总热阻。这与文献［1，2］得出的结论是一致的。

钠、管壁材料的物性参数来自文献［1，11］；一、二回路的传热系数计算公式来自文献［9］。

3 中间热交换器瞬态模型

用来描述中间热交换器瞬态变化较好的模型应包括一、二回路入口流量、温度变化带来中间热交换器内部、出口温度变化的数学模型，同时，应选取一种计算迅速、易于使用、误差小的计算方法。根据上述讨论，描述中间热交换器的能量守恒偏微分方程组为方程（3）的形式。

其中，密度ρ、比热C、传热系数U，均为温度的函数。

在每个节段上，将方程（3）离散为差分方程（4）：

对方程（4）这种差分方法进行了稳定性分析，将方程（4）展开，并转化为方程（5）的形式。

设3n－3维向量T＝（Tp，Tm，Ts），也即：

那么差分方程（5）可以写成方程（6）的形式，简写为MT′＝NT，其中A－G均为系数矩阵。

根据差分方程组（4）依次建立每个节段上的模型，如图5所示。并根据上述文献及稳态计算结果计算出每个节段上的物性参数与各微分方程组的系数。

图5 第i个节段上的瞬态计算模型Fig．5 Transient state model of segment i in IHXs

通过本文中的瞬态模型中变量取值，带入上述矩阵方程分析，在各种工况下增长矩阵M－1N的谱半径始终小于1，符合Von－Neumann条件，故差分格式是稳定的。

根据计算出来的每个微分方程组的系数，可得方程组的最大刚性比达106左右，对于这种刚性常微分方程组，采用ode15s方法求解，选取相对精度为10－4。

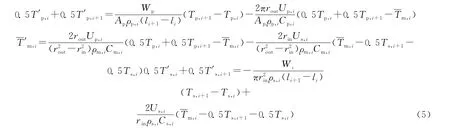
采用这种模型和算法，在其他参数均不变，对于为了便于比较，使输出量趋于同一方向，输入量分别选取100%功率工况下：一次侧流量阶跃降低5%、二次侧流量阶跃上升5%、一次侧入口温度阶跃降低5%及二次侧入口温度阶跃降低5%，对一、二次侧出口温度影响分别如图6、图7所示。

图6 一回路出口温度Fig．6 Temperature at primary outlet

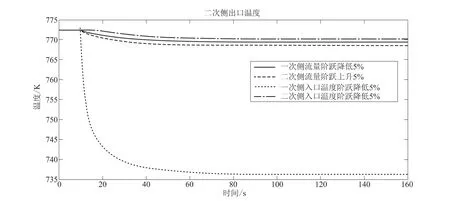
图7 二回路出口温度Fig．7 Temperature at secondary outlet

计算结果表明：

（1）流通延迟

一次侧入口温度对其出口温度影响有约6s的延迟、二次侧（中间回路）入口温度对其出口温度有约2．9s的延迟，这与文献［12］中相应的分别有5．8s、2．9s延迟的结论一致的；

（2）一次侧出口温度

二次侧入口温度对一次侧出口温度影响较之其他3个参数的影响大。二次侧入口温度阶跃降低后，一次侧出口温度迅速降低，经过约80s稳定在最终值附近。二次侧入口温度降低约29．2K，一次侧出口温度降低约23．5K，这与稳态计算结果相差较小，这是因为，如图5，在瞬态模型建立中将钠温度、流量对传热系数的影响加入到相应的程序中。

图8 一回路流量衰减工况计算结果Fig．8 Simulation result of loss of primary flow transient

一、二次侧钠流量对一次侧钠出口温度的影响均较小，约5K，且动态响应过程也类似，经过约90s一次侧出口钠温稳定在最终值附近；一次侧入口温度对其出口温度影响较之钠流量的影响稍大，动态响应过程也稍长一些，经过约100s稳定在最终值附近；

（3）二次侧（中间回路）出口温度

一次侧入口温度对二次侧（中间回路）出口温度影响较之其他3个参数的影响大。一次侧入口温度阶跃降低后，二次侧出口温度迅速降低，经过约90s稳定在最终值附近。一次侧入口温度降低约39．4K，二次侧出口温度降低约36．5K，这与稳态计算结果相差很小。一、二次侧钠流量和对二次侧出口温度影响均较小，并且过程较为缓慢、平滑，经过约90s稳定在最终值附近。

另外，在一回路钠流量以时间常数为15s指数衰减的工况下进行计算，给出了一、二次侧温度的25s、50s、75s时的计算结果，如图8所示，其中各组曲线中温度较高的为一次侧、较低的为二次侧。

4 结论及展望

本文使用Matlab／Simulink软件建立的中间热交换器模型，两种稳态计算方法计算出的符合性很好，与实际差别较小。瞬态模型计算迅速、数值稳定。与以往的中间热交换器建模方法相比，本文给出的两种稳态计算模型考虑了各物性参数变化对计算结果造成的影响。瞬态计算模型考虑了流量及钠温变化对换热系数造成的影响，适用于大扰动的计算，例如主泵堕转流量衰减。同时，瞬态模型采用Simulink模块库中的模块建模，从而避开了具体算法程序的编写，可以方便地对模型进行修改。因此本模型可用于中间热交换器的热工水力设计以及快堆核电厂的控制系统设计中。

未来将在中国实验快堆（CEFR）的试验中对本模型进行验证，或者在其他公开文献中获得数据对其进行验证。

同时，将进一步对中间热交换器建模仿真进行研究，从一维向三维热工、水力耦合模型扩展，从正常工况向自然循环工况扩展，从而获取一种更为精确的模型。

［1］ 苏著亭，叶长源，阎凤文，等．钠冷快增殖堆［M］．北京：原子能出版社，1991：332，361－362．

［2］ Tang Y S，Coffield Jr R D，Merkley R A．Thermal Analysis of Liquid Metal Fast Breeder Reactors［M］．ISBN 0894480111．La Grange Park，Illinois，USA：American Nuclear Society，1978．319－332，369－373．

［3］ Devlin R W，Bresnahan J D．FFTF and CRBRP intermediate heat exchanger design，testing，and fabrication［C］．Seminar on LMFBR components，Canoga Park，CA，USA，1977

［4］ CheungA C，Kao T T，Cho S M，et al．A Comparison of Between DEMO 1－D and the COMMIX 3－D Analysis of the CRBRP－IHX Under a Natural Circulation Event［C］．21st ASME／AIChE National Heat Transfer Conference．Seattle，Washington，USA，1983．

［5］ GunbyA L．Intermediate Heat Exchanger Modeling for FFTF Simulation［R］．AEC Research ＆Development Report of Battle Northwest Library．BNWL－1367，1970．

［6］ Brukx J F L M．CSDT Simulation Model for Prediction of IHX Transient Behavior Using S／360CSMP［D］．Delft，Netherlands：Delft University of Technology，1974．

［7］ 段天英．中国实验快堆控制系统的仿真研究［D］．中国原子能科学研究院博士学位论文，1999．

［8］ 段天英．热交换器仿真模型的修正［J］．中国试验快堆年报，2000：5．

［9］ Constantine P，Tzanos．Liquid－Metal Fast Reactor Breeder Beactor Intermediate Heat Exchanger Transient Modeling for Faster than Real－Time Analysis［J］．Nuclear Technology，1987，76（3）：337－351．

［10］ Constantine P，Tzanos．Validation of an Intermediate Heat Exchanger Model for Real Time Analysis［C］．American Nuclear Society and Atomic Industrial Forum Joint Meeting．Washington DC，USA，1986．

［11］ 居怀明，徐元辉，李怀萱．载热质热物性计算程序及数据手册［M］．北京：原子能出版社，1990：92－99．

［12］ 中国实验快堆最终安全分析报告［R］．中国原子能科学研究院，2008．