应变计组的应力应变转换

黄 浩

(1.河海大学水文水资源与水利工程科学国家重点实验室,江苏南京 210098;2.河海大学水利水电学院,江苏南京 210098)

应变计组的应力应变转换

黄 浩1,2

(1.河海大学水文水资源与水利工程科学国家重点实验室,江苏南京 210098;2.河海大学水利水电学院,江苏南京 210098)

为提高应力应变转换最终应力结果的准确度,根据应力应变转换的一般步骤,分析了其中基准时间选取、无应力计可靠性分析、徐变参数公式拟合、应力增量加载方式和应变计组平衡等关键问题,结果表明:基准时间选取缺少一个科学合理的定量原则;无应力计可靠性分析缺少一个可行的分析评判准则;徐变参数公式拟合应该采用全局优化算法;应力增量加载方式应该采用中点瞬时加载终点结束,得到终点时刻应力的方式;对于应变计组平衡问题,基于概率论将平衡问题转化成最优化问题,提出了最优化平衡法,数学实验结果证明该方法是一种科学合理的平衡方法。

应变计组;应力应变转换;基准时间;无应力计;徐变参数;加载方式;应变平衡

为了监控混凝土坝的安全,掌握其运行规律,指导施工和运行及反馈设计,一般要在大坝上设置环境量、变形、渗流和应力应变及温度等监测项目。这些监测项目互相结合组成一个完整的大坝监测系统,共同为大坝的安全服务。由于大坝变形量比较直观,实际应力成果又存在精度问题,故往往只重视变形监测,轻视应力应变监测。混凝土坝的强度破坏和失稳破坏实质上都是因坝基或坝体的应力超过材料或基岩强度造成的,过大的应力会导致大坝开裂和局部破坏,这往往是大坝最终破坏的直接诱因;同时大坝的变形和应力之间没有完全的因果关系[1],不能用变形完全反映应力;此外在大坝施工期,往往也没有变形监测,因此,应力应变监测对大坝安全评估十分重要。

对于混凝土坝的应力应变监测,目前还不能直接测量混凝土内的应力,特别是容易引起裂缝的拉应力,通常只能通过应变计监测混凝土应变,然后通过应力应变转换来获得混凝土应力[2-3]。由于应力应变转换的环节众多,各个步骤带入的误差以及误差的传播,使得根据应变资料计算所得的最终应力结果准确度降低,这是混凝土坝应力应变监测中不可忽视的问题。本文根据应力应变转换的一般步骤,总结分析了其中可能降低最终应力结果准确度的关键问题,给出了一些科学适用的建议,同时对应变计组平衡进行了深入的分析,提出了一种科学合理的平衡方法。

1 应力应变转换中的关键问题

应力应变转换总的包括3个步骤:(a)原始监测数据的误差分析和处理;(b)单轴应变计算;(c)徐变应力计算。原始监测数据的误差分析和处理非常重要,它是单轴应变和徐变应力计算的基础,对最终应力结果影响很大。原始监测数据的误差包括粗差、系统误差和偶然误差。粗差和系统误差对计算影响较大,必须处理,可以对单支应变计和整个应变计组进行误差检验[2],对能确定原因并且能定量的误差可对其修正,对无法修正的应该舍弃不用。偶然误差虽然对计算影响较小,但也不容忽视,可以通过应变计组平衡予以处理。但不合理的应变计组平衡方法不能很好地消除实际的偶然误差,故应变计组平衡应是应力应变转换中的一个关键问题。单轴应变计算主要包括应变数据的整编和应力应变的计算,其中的关键问题有基准时间选取和无应力计可靠性分析等。计算徐变应力通常采用变形法,该方法的关键问题有徐变参数公式拟合和应力增量加载方式等。

1.1 基准时间选取

基准时间选取在应力应变转换中既是第一步,又是至关重要的一步,这里产生的误差将会影响整个转换过程。所谓基准时间就是应变计在混凝土内开始工作的时间,即混凝土的刚度刚好等于应变计刚度的时刻,此时混凝土能带动应变计共同变形,应变计可以监测混凝土的应变。基准时间不仅是应变计监测数据整编的基准时间,也是应力应变转换的起点,基准时间选取的误差越小,最终得到的应力就越准确。如果选取的基准时间比实际滞后,将导致转换出的应力偏大[4]。一般选取混凝土的终凝时刻作为基准时间,因为此时混凝土的弹性模量接近应变计的弹性模量,已能带动应变计一起工作。但终凝时间与水泥品种、浇筑温度和气温因素有关,没有一个确定时间,一般在12～24 h之间,所以对于每支应变计都应根据实际情况分别选取基准时间,一般原则是通过过程线选择测值不再跳动,电阻比和温度能够对应变化的时刻作为基准时间。对于同一应变计组,它的每支应变计和对应的无应力计的基准时间应选取同一时刻。

对于应变计组,选取基准时间虽然只是一次性的工作,但是对于每支应变计都要具体情况具体分析,而目前新建的混凝土大坝通常都布置了几百支应变计,总的工作量较大;同时选取基准时间的一般原则——“测值不再跳动,电阻比和温度能够对应变化”,还是比较定性的描述,而实际应变计刚开始的测值跳动比较复杂,故实际选取基准时间时就带有较大主观性,这必将导致选取的基准时间产生误差。因此,有必要寻找一个科学合理的定量原则去选取基准时间以克服人的主观性,减少选取基准时间的误差,便于计算机实现,从而可以便捷地计算出更加准确的应力。彭虹[5]提出将混凝土初期温度增长速率下降的时刻作为混凝土终凝时刻,同时又提出用能量法去推求混凝土终凝时刻,这两个方法都是定量选取基准时间的,且便于计算机实现,但对这两种方法的科学性和合理性还有待进一步研究。

1.2 无应力计可靠性分析

由应变计算混凝土内的实际应力,必须使用混凝土应变中的应力应变,即荷载和内部约束引起的应变,它等于应变计实测应变减去混凝土的自由体积变形。混凝土的自由体积变形是混凝土在不受外力的情况下,由于温度和湿度的变化以及水泥的水化作用产生的体积变形,可以由无应力计测出。其中水泥的水化作用产生的体积变形,即混凝土的自生体积变形,主要是水泥在水化过程中由于化学作用而产生的变形,随着水化过程的结束而逐渐趋向结束。混凝土温度可以加快和减缓自生体积变形的过程,与温度对水化热过程的影响类似,但不应发生逆向反应。因此一般自生体积变形过程,无论是收缩或膨胀,基本上应是单调变化,尤其不应在水化过程基本结束后还发生周期性变化[6]。正是因为混凝土的自生体积变形具有单调特点,所以无应力计可靠性分析就是通过分析其自生体积变形部分变化规律来判断无应力计测值是否可靠有效。

对于混凝土大坝,应变计所在的混凝土属于大体积混凝土,其自由体积变形通常可以忽略湿度的影响,所以只要从无应力计测值中扣除混凝土的温度变形,便可近似得到混凝土的自生体积变形。混凝土的温度变形可以用混凝土膨胀系数乘以对应的温度变化得到,而且当无应力计和工作应变计的温度不同时,也要通过混凝土的膨胀系数进行二者温度变形的修正,因此准确计算混凝土膨胀系数就显得十分关键。混凝土膨胀系数一般可以通过无应力计资料分析[5]或者室内试验获得,通过室内试验获得混凝土膨胀系数精确、工作量少,但不能反映混凝土大坝不同部位的真实混凝土膨胀系数,用于计算会产生误差;而通过分析无应力计资料获得混凝土膨胀系数虽然工作量大,精度可能没有试验高,但能反映应变计所在混凝土真实膨胀系数,用于计算产生的误差反而较小。其中通过统计回归模型获得混凝土膨胀系数的方法人为主观性小,且便于计算机实现,是一个值得推广的方法。

实际由无应力计测得的混凝土的自生体积变形往往并不是预期的单调变化,而是有波动起伏的,如图1所示(图1为某一混凝土坝块的3支无应力计分离出的自生体积变形和同标号混凝土室内试验值过程线)。

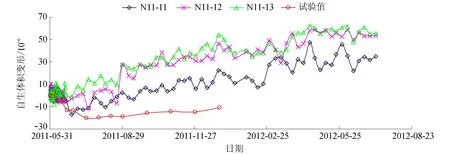
图1 混凝土自生体积变形现场实测值与室内试验值对比Fig.1 Comparison of field-measured values and laboratory test values of concrete autogenous volume deformation

从图1可以发现:(a)试验值和实测值有很大差别,而且3个实测值虽然趋势性相同,但也是有区别的。虽然是同种混凝土,但由于每支应变计所在混凝土的周围环境并不完全相同,所以它们所测的混凝土自生体积变形应该是有差别的,这种差别的机理目前并不清楚,无法判断其是否合理。(b)实测值有比较明显的波动起伏。波动起伏的原因可能有多种,如湿度的影响、仪器的稳定性、施工影响、无应力计受力[6-7]等,具体如何判别和处理目前也没有很好的方法。这些问题的存在给无应力计的可靠性分析带来了困难,同时也降低了最终应力结果的可信度。因此,科学便捷地处理这些问题对减少应力应变转换误差,提高应力结果准确度至关重要。

1.3 徐变参数公式拟合

混凝土徐变应力计算用到的徐变参数包括混凝土的弹性模量和徐变度,对其进行公式拟合,是用于徐变应力计算中确定任意时刻的徐变参数。采用公式拟合计算与过去采用的插值计算相比,具有3个优点:一是计算时段的划分可以更加灵活,从而充分利用监测数据;二是公式拟合把握住了弹性模量和徐变度的总体趋势,得出的值更接近真实值,误差小,特别对于试验值的外延更加科学合理;三是便于计算机计算,加快计算速度。

目前在徐变参数拟合公式中,弹性模量和徐变度拟合效果较好的公式[8-10]有

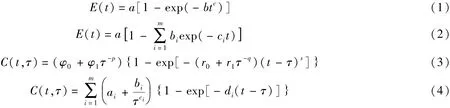
式中:E(t)——t时刻的混凝土弹性模量;C(t,τ)——τ时刻加载持续到t时刻的混凝土徐变度;m——指数函数复用次数,一般取2即可;其他均为要拟合的系数。

公式(2)和(4)都是简单指数函数的叠加,它具有指数函数无记忆的特点,用于计算不需记忆应力历史,只需一递推公式即可,这一点对于有限元计算结构徐变应力大有帮助,减少了大量存储单元[9],但对于应力应变转换意义不大。从上面的公式可以看出徐变度的拟合公式相对复杂,参数较多,为了获得最好的拟合效果,一般采用优化方法[9-10]。

为了保证后续计算的准确性,弹性模量和徐变度的公式拟合就显得相当重要。但文献[9-10]给出的优化方法只能得出局部最优解,所以应该采用遗传算法、粒子群算法等全局优化算法进行公式拟合,使结果达到真正的最优。需要注意的是:在拟合公式前,应该检查试验值的可靠性,否则最后优化计算得到的结果可能不符合混凝土的一般规律,例如:标号低的混凝土最终弹性模量反而比标号高的混凝土大。

1.4 应力增量加载方式

用变形法计算徐变应力的关键是求承前应变,承前应变根据叠加原理计算:

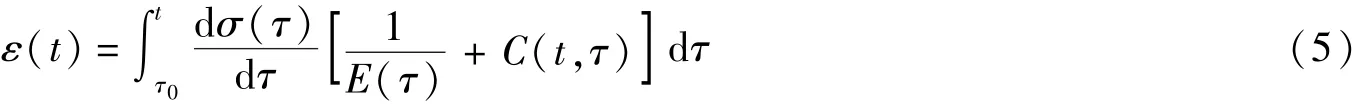
式中:ε(t)——t时刻的承前应变,即t时刻前的应力产生的应变;τ0——基准时刻;σ(τ)——τ时刻混凝土内的应力。

实际计算中,是将式(5)的积分转化成分段求和进行近似计算,所以计算前应将整个应变过程划分为多个小的计算时段。过去都是人为划分计算时段,早期应力增量较大,时段应细些,后期应力变化不大,时段可以粗些。现在一般都直接将应变观测时刻作为分隔点进行时段可以划分,这样做不仅划分简单,充分利用了监测数据,而且时段划分得足够精细,计算结果更精确。

计算时段划分完成后,如何准确计算每个时段的应力增量就是关键,目前对变形法的改进[4,11]就是针对应变增量的计算,其实质就是改进加载方式。加载方式不同主要体现在加载点、应力计算点、应力增加方式的区别,如图2所示。图2中方式1是起点瞬时加载中点结束,得到的是中点时刻的应力,它是目前最常用的加载方式;方式2是中点瞬时加载终点结束,得到的是终点时刻的应力,文献[4]对时段划分的改进实质是将方式1的加载方式变为了方式2;方式3是起点瞬时加载终点结束,得到的是终点时刻的应力,它可以看成是方式1和方式2计算时段的一半的放大;方式4是起点线性加载终点结束,得到的是终点时刻的应力,它是文献[11]采用的加载方式。分别采用上面4种加载方式对某一九向应变计组的监测数据进行计算,得到应力结果如图3所示。

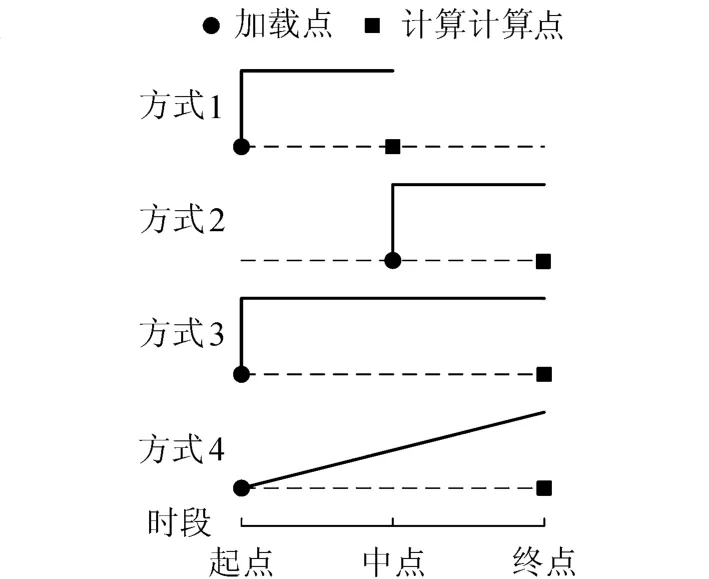
图2 不同加载方式Fig.2 Different loading methods

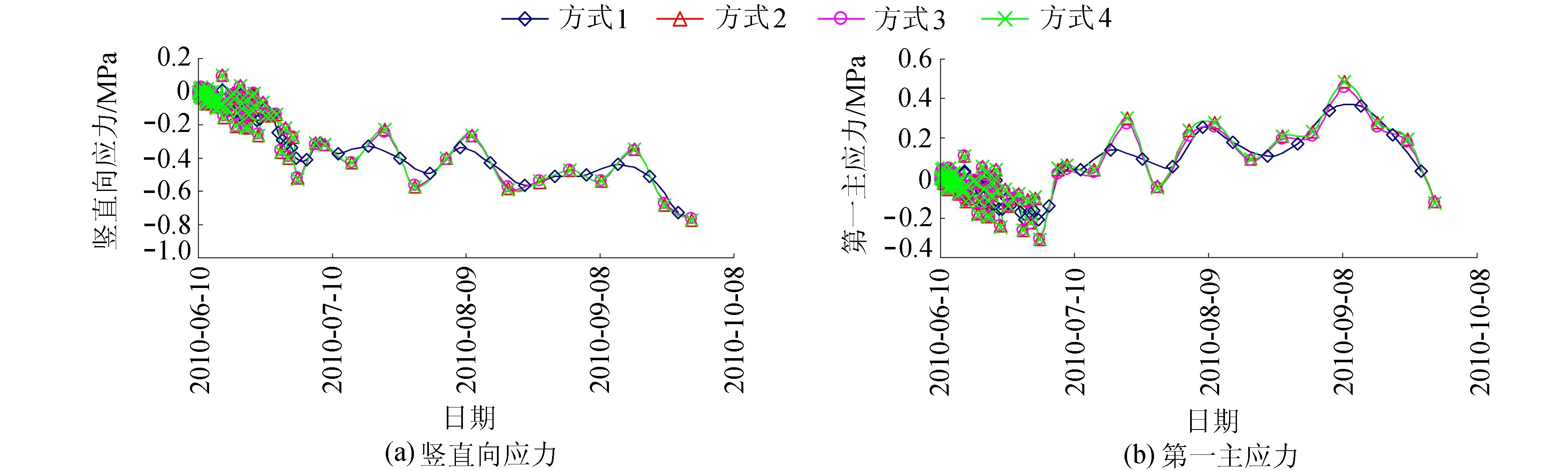
图3 不同加载方式计算结果对比Fig.3 Comparison of results of different loading methods

从图3可见:(a)方式1的结果与其他3个差别较大,主要是因为方式1用于计算应力增量的应变是中点应变,取为起点和终点应变的平均,故所得的应力过程线较平滑,最大应力偏小;(b)方式3的结果虽然比方式1的好,但较方式2的应力绝对值还是偏小,主要是因为方式3是起点加载,对应的时段有效弹性模量较方式2小,故所得的应力增量较小;(c)方式2和方式4的结果非常相近。综上,实际计算中不宜采用方式1和方式3,虽然文献[11]推荐采用方式4,但线性增加未必能很好地刻画实际应力的复杂变化,而且方式4多了一步积分,也会存在误差,同时方式2和方式4的结果差别不大,故推荐采用方式2。

2 应变计组平衡

2.1 平衡的必要性和原理

由于观测误差及应变计组各支应变计并不是在一个几何点上,故应变计组各向应变并不完全满足应变张量第一不变量——空间中一点3个互相正交方向的应变之和为常量。由应变张量第一不变量可以推出同一平面内两组正交方向的应变之和的差为零,但实际观测两者之差并不为零,这就产生了平面应变不平衡量Δ。当观测误差较小而且是随机的偶然误差时,应变不平衡量Δ是一个可正可负的随机变量,其绝对值不会大于观测系统均方差的3倍。应变计组平衡就是根据应变张量第一不变量原理对上述的偶然误差进行检验和修正。应变计组平衡有两点好处:一是减少了观测系统偶然误差的影响,使最终的应力结果更加接近真实值;二是在忽略计算误差的情况下,由应变计组平衡最终计算出来的各向应力满足应力张量第一不变量。

可见,应变计组平衡在整个应力应变转换过程中是非常必要和关键的,这一步的处理对最终应力结果也有较大影响,但目前关于应变计组平衡的研究还很少,往往只给出一个平衡公式[2,12-13],并没有深入地探讨其科学性。从文献[2,12-13]可知,对于同一应变计组的平衡方法并不唯一,实际上应变计组的平衡方法可以有无数种。对于如图4所示的九向应变计组平衡就是解方程组:

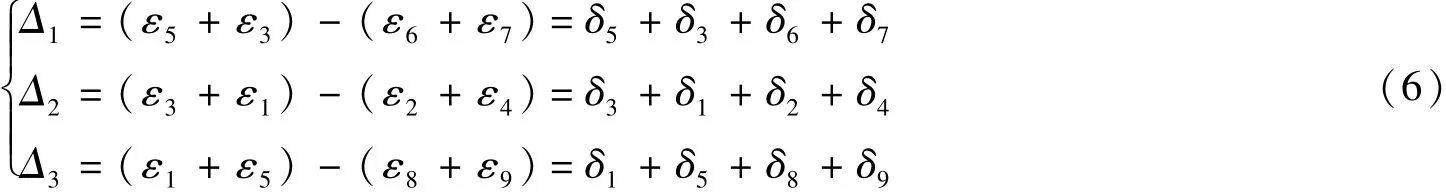
式中:εi——i向应变计实测应变;Δ1、Δ2、Δ3——yOz、zOx、xOy面的应变不平衡量;δi——i向应变平衡修正值。

这个方程组有9个未知数,但只有3个方程,所以解有无数个,即应变计组的平衡方法可以有无数种。

2.2 最优化平衡法

虽然应变计组的平衡方法可以有无数种,但是每一种平衡方法只能完全修正特定一类组合的误差,即平衡后的应变值等于真值。然而应变计组的实际误差是未知的,故不能有针对性地选择最佳平衡方法进行平衡,而且这也是不现实的。因此,应该寻找一种平衡方法,能较好地修正大多数应变计组误差,即多数实际应变观测值经平衡后得到的应变值能更接近真值。

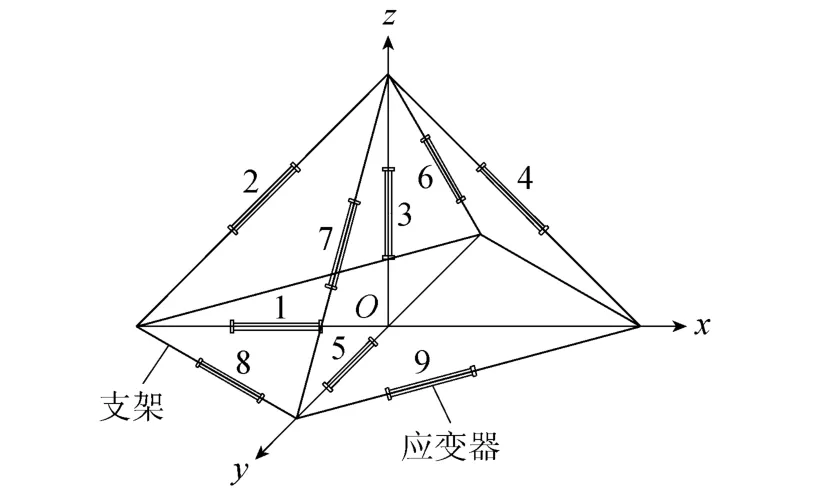
图4 九向应变计组Fig.4 Nine-direction strain gauge set

应变计组平衡是用来修正应变计观测的偶然误差的,这种误差服从均值为零的正态分布,误差的绝对值越大,其发生的概率越小。实际误差大多数是出现概率较大的误差,因此,要能较好地修正大多数应变计组误差,应以各向平衡修正误差发生概率之和f(δ)最大为目标,这样应变计组平衡问题就转化成最优化问题,并把这种平衡方法称为最优化平衡法。

假设应变计组的各应变计等精度,其偶然误差都服从N(0,σ2)分布,对于图4所示的九向应变计组的平衡可以转化成式(7)所示的最优化问题,直接求解该问题比较麻烦,可以对其中f(δ)进行泰勒展开并只取前两项,将问题简化成式(8)所示的最优化问题,对其可以通过Lagrange乘子法进行求解,十分简单。

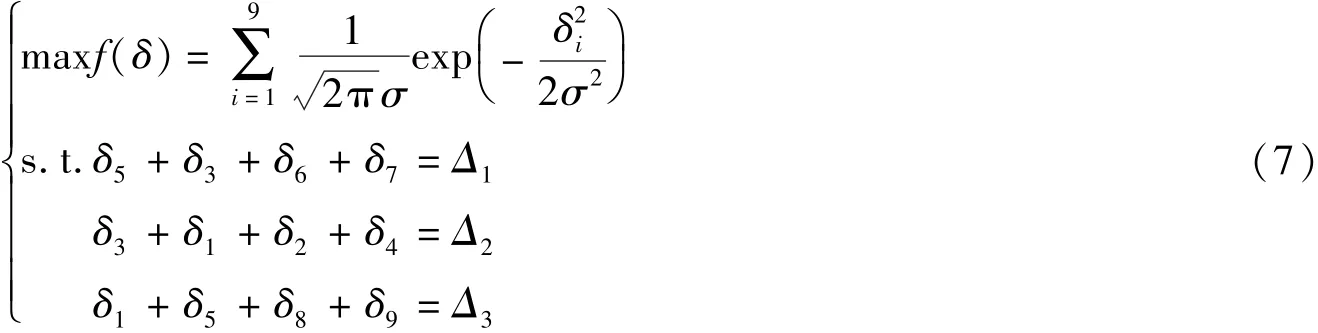
2.3 数学实验

为了验证应变计组平衡的必要性和所提出的最优化平衡法的合理性,设计了一个数学实验。实验步骤如下:

a.取一个九向应变计组的监测应变数据,其数据序列长度为50,对其采用任意一种平衡方法进行平衡,并将平衡后应变值作为应变真值。

b.对应变真值采用matlab的normrnd函数生成一个具有正态偶然误差的应变值,并将其作为该九向应变计组的原始观测应变值。

c.对原始观测应变值分别用3种不同的平衡方法进行平衡,其中平衡方法1为文献[2]提供的方法,平衡方法2是根据文献[12]原理推导的九向应变计组平衡方法,平衡方法3是本文提出的最优化平衡法。

d.重复第b,c步1000次,3种平衡方法分别得到1000组,即50000组平衡应变值,然后分别计算每组平衡应变值与应变真值的误差,即各向误差的平方和,比较3个误差,找出误差最小的平衡方法。

e.对上面得到的应变真值及最后一次得到的原始观测应变值、3种平衡应变值分别进行徐变应力计算,并将由应变真值计算得到的应力作为应力真值。

f.对第d步结果,统计3种平衡方法平衡误差最小的组数,对第e步得到的应力真值与其他4种应力值做相关分析。

实验结果:50000组应变计组误差中,平衡后的应变值最接近应变真值的,3种平衡方法分别有10199、10600和29201组;竖直向应力和第一主应力的相关分析结果如图5所示。

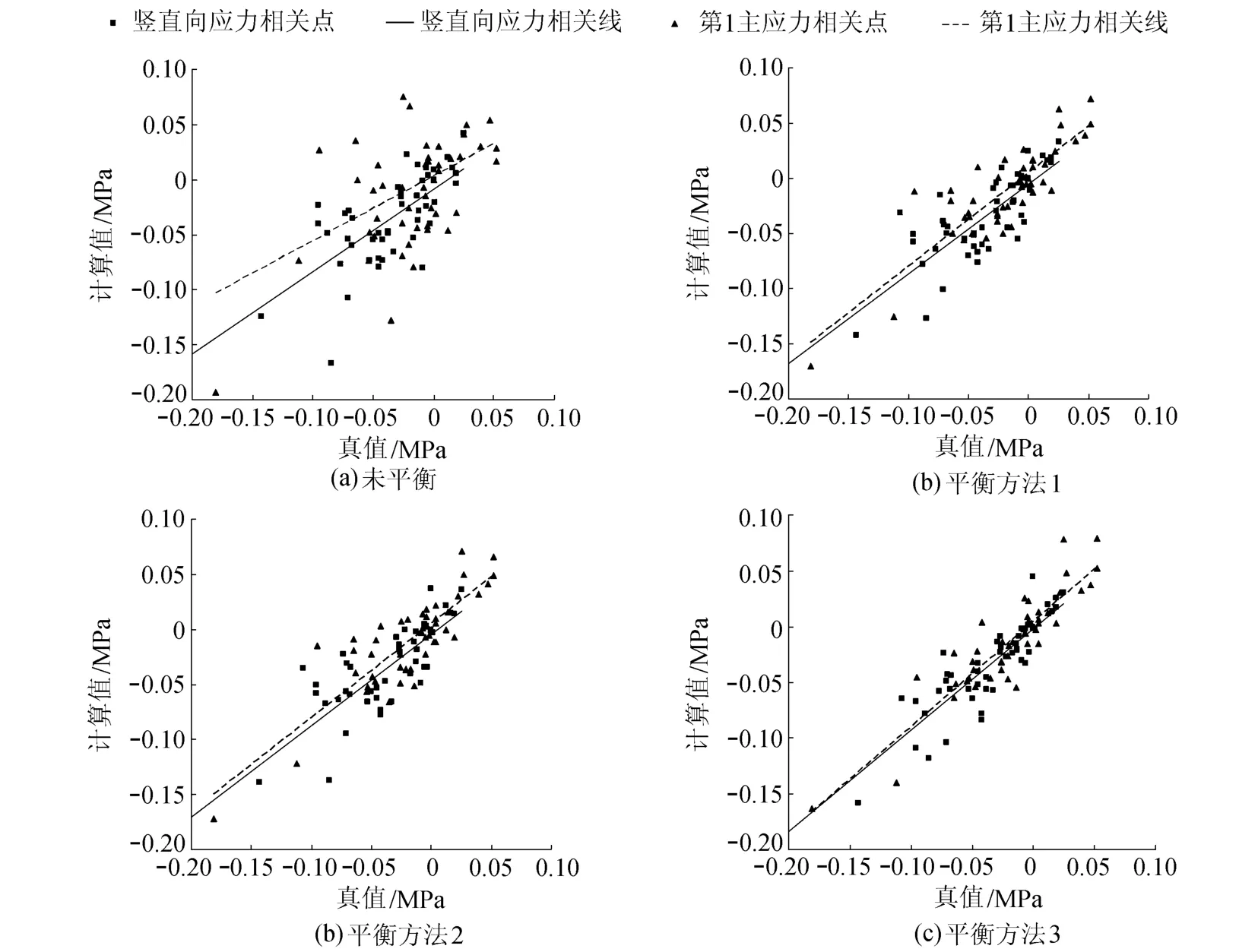
图5 不同平衡方法计算值与真值的关系Fig.5 Relationship between true values and calculated values using different balance methods

实验结论:(a)由未平衡的应变值,即原始观测应变值,计算出来的应力值和真值的相关性较差,误差较大,第一主应力的相关系数仅为0.4469,而平衡得到的应力结果最差的相关系数也达到了0.847 6,故进行应变计组平衡十分有必要;(b)3种平衡方法中,最优化平衡法效果最好,应变平衡误差最小的组数差不多是其他两种方法的3倍,同时得到的应力与真值的相关性最好,竖直向应力和第一主应力的相关系数分别高达0.8963和0.9034,可见最优化平衡法是一种科学合理的平衡方法。

3 结 语

在应变计组的应力应变转换中,为了确保最终应力结果的准确度,应特别注重基准时间选取、无应力计可靠性分析、徐变参数公式拟合、应力增量加载方式和应变计组平衡等关键问题,尽量减少其可能产生的误差。目前基准时间选取缺少一个科学合理的定量原则;无应力计可靠性分析缺少一个可行的分析评判准则;徐变参数公式拟合应该采用全局优化算法;应力增量加载方式应该采用中点瞬时加载终点结束,得到终点时刻应力的方式。应变计组平衡十分必要,显著提高了最终应力结果的准确度;基于概率论的最优化平衡法具有科学的理论基础,平衡效果明显优于现有的平衡方法,是一种科学合理的平衡方法。

[1]储海宁.关于高混凝土坝应力应变监测的几个问题:兼评安全监测规范的有关规定[J].大坝与安全,2009(2):29-37.(CHU Haining.Several issues on stress and strain monitoring of high concrete dams:discussion on some specifications in safety monitoring norm[J].Dam and Safety,2009(2):29-37.(in Chinese))

[2]储海宁.混凝土坝内部观测技术[M].北京:水利电力出版社,1989:162-194.

[3]沈振中,苏怀智,吴中如.二滩工程混凝土观测应变和应力的计算[J].水利水电技术,1999,30(9):11-13.(SHEN Zhenzhong,SU Huaizhi,WU Zhongru.Concrete observation strain and stress calculation in the Ertan Project[J].Water Resources and Hydropower Engineering,1999,30(9):11-13.(in Chinese))

[4]张雄,陈胜宏,傅少君,等.变形法计算混凝土应力的改进[J].水力发电学报,2010,29(6):187-192.(ZHANG Xiong, CHEN Shenghong,FU Shaojun,et al.Modification to deformation method of stress computation of concrete[J].Journal of Hydroelectric Engineering,2010,29(6):187-192.(in Chinese))

[5]彭虹.混凝土无应力变形中几个问题的探讨[J].大坝观测与土工测试,1983(2):10-18.(PENG Hong.Several problems of no-stress deformation of concrete[J].Dam Observation and Geotechnical Tests,1983(2):10-18.(in Chinese))

[6]王同生.混凝土自生体积变形与无应力计[J].水利规划与设计,2009(5):38-40.(WANG Tongsheng.Concrete autogenous volume deformation and non-stress strain gauge[J].Water Resources Planning and Design,2009(5):38-40.(in Chinese))

[7]韩世栋,潘琳,赵斌.高应力对拱坝无应力计测值的影响分析[J].水电自动化与大坝监测,2011,35(5):49-52.(HAN Shidong,PAN Lin,ZHAO Bin.Influence of high stress on values of non-stress meter of arch dams[J].Hydropower Automation and Dam Monitoring,2011,35(5):49-52.(in Chinese))

[8]朱伯芳.混凝土的弹性模量、徐变度与应力松弛系数[J].水利学报,1985(9):55-61.(ZHU Bofang.Elastic modulus,creep degree and stress relaxation coefficients of concrete[J].Journal of Hydraulic Engineering,1985(9):55-61.(in Chinese))

[9]朱伯芳.关于混凝土徐变理论的几个问题[J].水利学报,1982(3):35-40.(ZHU Bofang.Several problems in the theory of creep in concrete[J].Journal of Hydraulic Engineering,1982(3):35-40.(in Chinese))

[10]朱伯芳.混凝土徐变方程参数拟合的约束极值法[J].水利学报,1992(7):75-76.(ZHU Bofang.The constrained extremum method of concrete creep equation parameters fitting[J].Journal of Hydraulic Engineering,1992(7):75-76.(in Chinese))

[11]冯波,张志诚,董霞.混凝土应力计算的变形法误差分析及方法改进[J].河海大学学报:自然科学版,2007,35(2):217-219.(FENG Bo,ZHANG Zhicheng,DONG Xia.Error analysis of deformation method for stress calculation of concrete and its improvement[J].Journal of Hohai University:Natural Sciences,2007,35(2):217-219.(in Chinese))

[12]郭晨.大坝内部七向应变计组平差公式的改进探讨[J].大坝观测与土工测试,1992(4):45-46.(GUO Chen.Modification to adjustment formula of seven-directions strain gauge set[J].Dam Observation and Geotechnical Tests,1992(4):45-46.(in Chinese))

[13]朱赵辉,包腾飞,汪亚超,等.应变计组的因果关系模型有效性判断算法研究[J].重庆建筑大学学报,2008,30(5):100-104.(ZHU Zhaohui,BAO Tengfei,WANG Yachao,et al.Validity judgment computation of a causal relation model of straingauge arrays[J].Journal of Chongqing Jianzhu University,2008,30(5):100-104.(in Chinese))

Stress-strain conversion of strain gauge set

HUANG Hao1,2
(1.State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering,Hohai University, Nanjing 210098,China; 2.College of Water Conservancy and Hydropower Engineering,Hohai University,Nanjing 210098,China)

In order to improve the accuracy of the final stress result in stress-strain conversion,we analyze some key problems,including the reference time selection,non-stress gauge reliability,formula fitting of creep parameters,stress increment loading mode,and strain gauge set balance,according to general steps of stress-strain conversion.The analysis results show that the reference time selection lacks a scientific and reasonable quantitative principle,the non-stress strain gauge reliability analysis lacks a feasible evaluation criterion,the formula fitting of creep parameters requires a global optimization algorithm,and the stress increment loading mode requires instantaneous loading at the midpoint and ending at the endpoint.Meanwhile,based on the probability theory,the problem of strain gauge set balance is transformed into an optimization problem,and an optimization balance method is put forward,and proven to be scientific and reasonable through a mathematical experiment.

strain gauge set;stress-strain conversion;reference time;non-stress gauge;creep parameters; loading mode;strain balance

TV698.1+1

:A

:1000-1980(2014)01-0073-07

10.3876/j.issn.1000-1980.2014.01.014

2013-01 05

国家自然科学基金(51279052);水利部公益性行业科研专项(201201038)

黄浩(1988—),男,安徽滁州人,博士研究生,主要从事水工结构与大坝安全监控研究。E-mail:senghuih@126.com