基于ADSP-TS201的大点数FFT实现
穆文争 王启智 朱子平
(中国电子科技集团公司第三十八研究所 合肥 230088)
0 引言
在雷达信号处理中,FFT作为是频域脉压和谱分析的基础,是较为常用的一种变换,一般由数字信号处理器完成。在工程应用中,当需要做FFT变换时,设计师可以调用开发环境自带的库函数,也可以将FFT做成公用基础模块,供设计者调用。此类模块一般采用汇编语言设计,针对所使用处理器的结构特征进行优化,具有较高的运算效率。但是当需要变换的FFT点数较大时,该类模块不再适用,因为输入数据和中间缓存都要占据很大的内存空间,而一般DSP的内存空间有限且被划分为多个不连续的block,这就破坏了该类模块的并行运算结构,降低了运算效率,如果采用与外部存储器交换数据的办法,由于与外存交换数据的速度较慢,也会降低运算效率。因此,在工程上需要做大点数FFT的场合,就要考虑如何实现的问题。
本文首先介绍了大点数FFT变换的数学原理,即将一维FFT拆成二维FFT实现的算法原理,然后以96K点为例,介绍其在通用处理器ADSP-TS201上的实现过程。
1 数学原理
设有限长序列x(n)的长度为N,则其DFT为
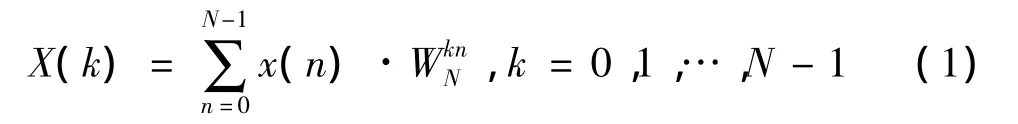
令N=N1N2,可以将x(n)分解为N2个长度为N1的序列,将这些序列用阵列x'表示,则
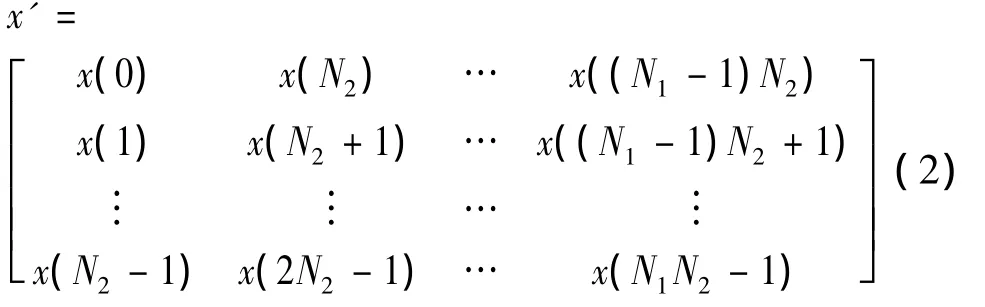
令n和k的序号映射定义如下:
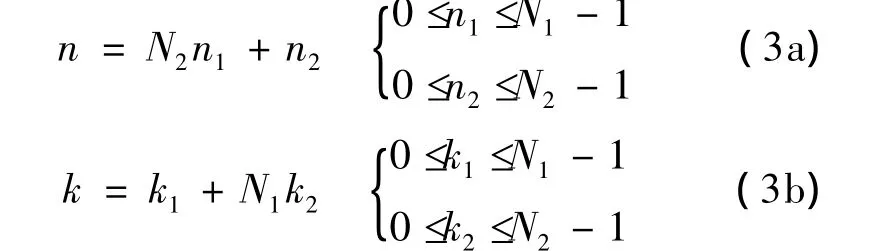
则N点DFT可以表示为:
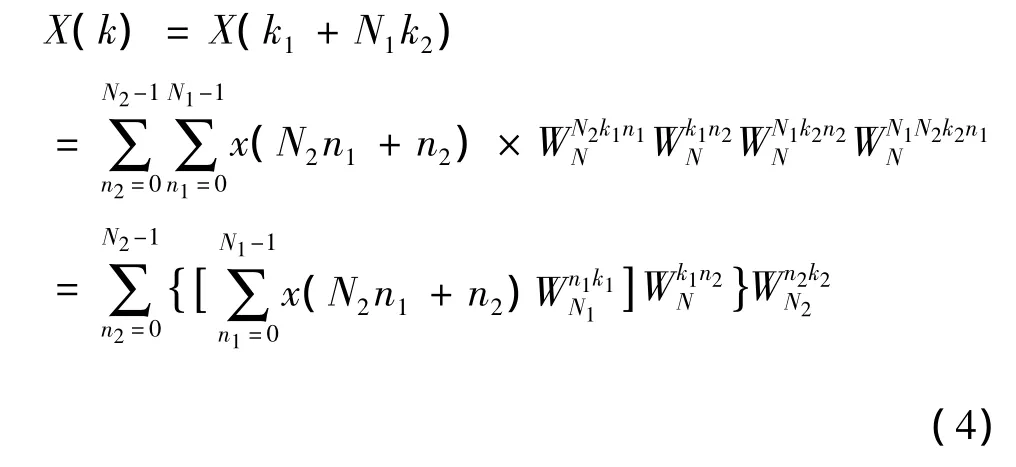
令
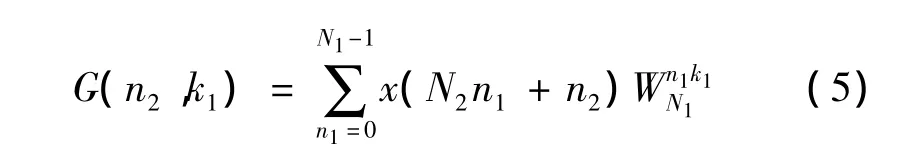
则G(n2,k1)为序列x(N2n1+n2)的N1点 DFT,即上式二维阵列N2行元素的DFT。计算阵列x'每一行N1点DFT就得到另一个矩阵:

矩阵的元素为复数G(n2,k1)。因n2行的数据在计算完x(N2n1+n2)的N1点DFT后不再需要,所以G(n2,k1)可以存储在同一行。计算X(k),还应乘以旋转因子Wk1n2N形成新的阵列
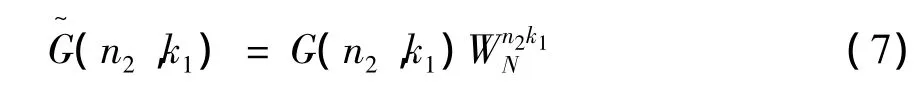
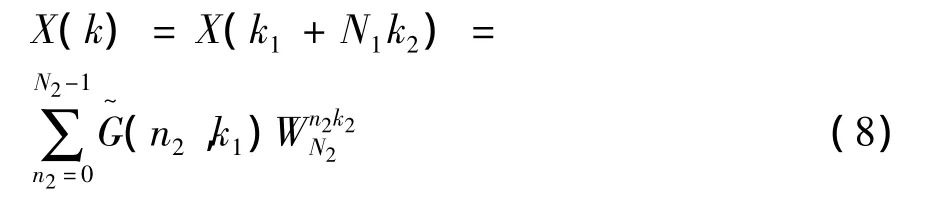
这样DFT变换结果就可由二维阵列得出。
由此可见,将一维FFT拆成二维FFT的实现过程就是将N点FFT分解为N2个N1点行变换与N1个N2点列变换的级联[2],经过二维拆分以后,设计师就可以调用已有的FFT函数。
2 工程实现面临的问题
除了输入数据和中间缓存要占据很大的内存空间外,做大点数FFT遇到的另外一个问题就是存储旋转因子。当变换的点数很大时,在FPGA或DSP中存储这些旋转因子需要很大的内存空间,这在工程实现上不方便。下面说明如何对旋转因子进行分解,以降低对内存的需求量。
如果将N分解为N1×N2,k分解为N1×α+β,其中α为倍数,β为余数。则有
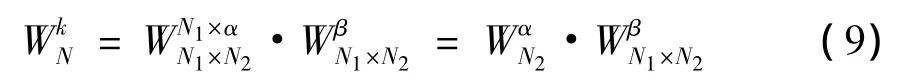
因为k<N,即N1·α+β<N1·N2,又β是k对 N1的余数,有0≤β≤N1-1 ,所以 N1·α < N1·N2,即α<N2。
以1M点FFT为例,N可以分解为N1×N2=1024×1024,这样存储的旋转因子个数就由1M点减少为1024+1024=2048点。
3 96K点FFT工程实现
以上对大点数FFT的实现方法做了原理性介绍,下面通过一个具体的例子,说明其在通用处理器ADSP-TS201上的实现过程。
由上述一维FFT拆成二维FFT的算法原理,可以归纳出大点数FFT实现的基本步骤[3]:
a.将N点输入数据表示成L行C列矩阵;
b.对矩阵所有列分别做L点FFT,得到G(l1,c);
c.将G(l1,c)乘以中间旋转因子得到GG(l1,c);
d.对GG(l1,c)所有行做C点FFT,得到X(c+l1×C);
e.将X(c+l1×C)整序为X(k),变换完成。
图1为大点数FFT实现流程图。
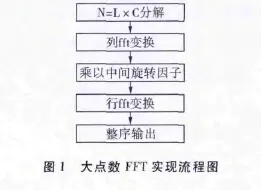
需要注意的是,数据输入分解和因计算中间旋转因子而进行的分解是两种不同的分解,它们可以不同。例如本例中,数据输入可以分解为96k=3×32k,计算中间旋转因子可以分解为96k=256×384。在对96k=N1×N2分解时,需要遵循一个原则,就是其中一个因子要为2的整幂次,因为这样便于利用ADSP-TS201的汇编指令FEXT快速提取α和β。
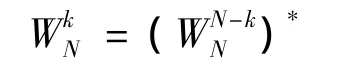
可知,旋转因子只需存储一半即可,另一半可由共轭对称性得到;在存储旋转因子时,由于 β 的范围是0~(N1-1),所以这N1个旋转因子要全部存储。这样需要存储的旋转因子个数就可以由(N1+N2)点减少为点,从而进一步减少了所需的内存空间。有了这两种旋转因子,计算大点数FFT时任何一种旋转因子都可以通过(9)式实时生成。
表1是96K点FFT的N1和N2不同分解方式对应的旋转因子存储量,可见256×384是存储量最小的一种分解方式。
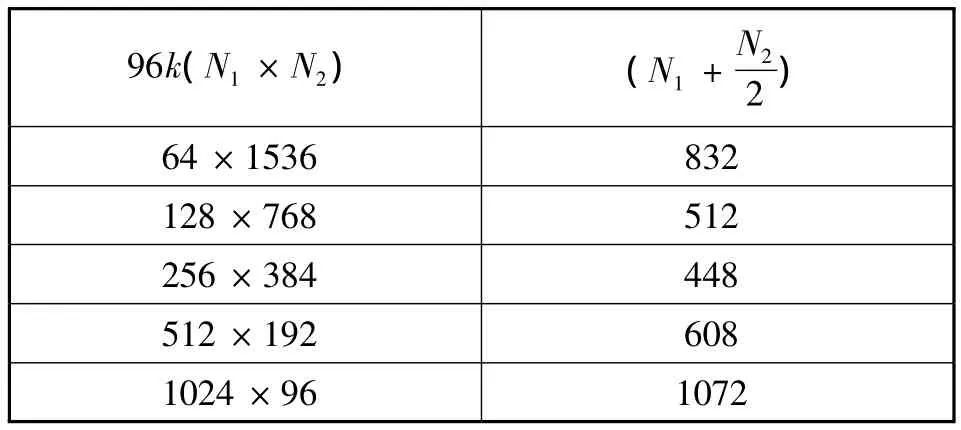
表1 不同分解方式对应的旋转因子存储量
由于所使用的处理器为ADSP-TS201,下面对该处理器的内存加以说明。ADSP-TS201具有24Mbit内存,被划分为 6个 block,每个 block为4Mbit(128K ×32bit),组织方式如下[4]。
在采用开发环境(VisualDSP++5.0)默认的链接描述文件时,block0用来存放代码,block4的部分空间用作堆栈,这样可供用户使用的完整的128K字内存块就只有4块,即 block2、block6、block8和block10。
处理96K点FFT时,由于一个block最多存储64K点复数,所以需要1.5个block作为输入数据缓存。可以考虑将96k点复数分为三段、每段32K点进行存储,其中一种存储方式如图3所示。
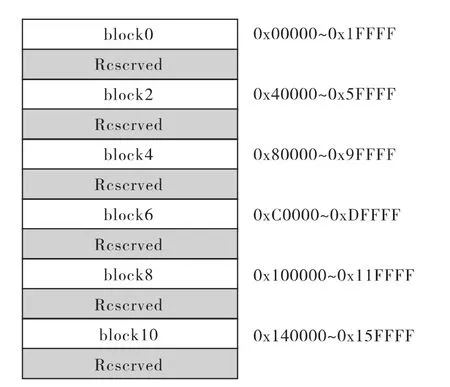
图2 ADSP-TS201的内存组织
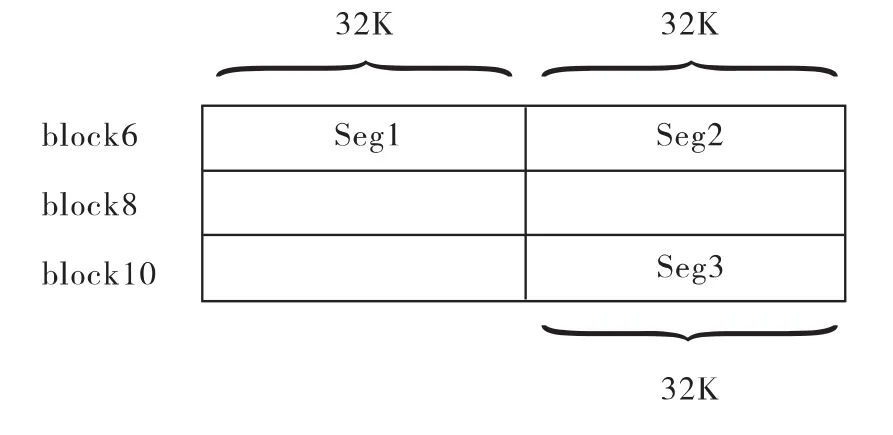
图3 96K点输入数据的缓存方式
下面按照前述的实现步骤,对96K点复数进行FFT变换。
第一步:
对输入的3段数据,先对每列做3点DFT,然后对做过DFT的数据乘以中间旋转因子。需要注意的是,每列3点数据所乘的旋转因子均不同,旋转因子的上标为行号×列号。乘积结果覆盖原数据见图4。
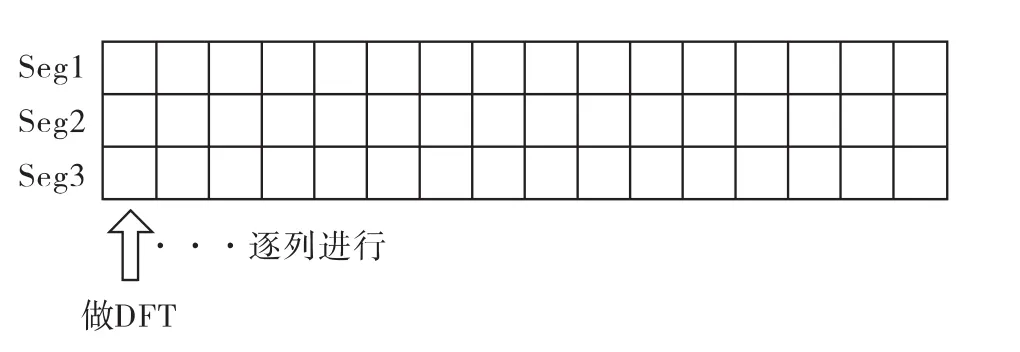
图4 每列3点DFT
每列旋转因子的上标见表2。

表2 旋转因子上标
第二步:
数据经过第一步处理后,再对每一行做FFT,结果仍然覆盖原数据,如图5所示。
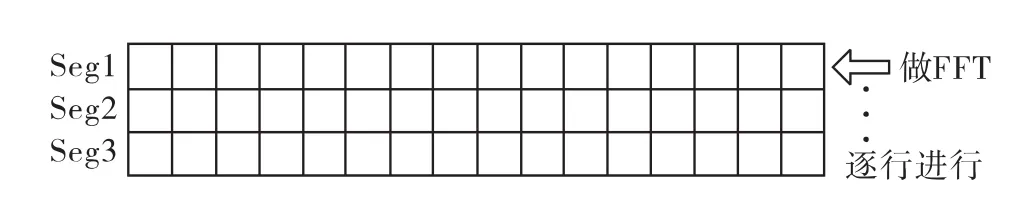
图5 每行做FFT
第三步:
将结果重新排序。由于DSP没有足够的内存用作缓存,所以重排只能分段进行,这样重排就需要两轮,重排示意图见图6。

图6 数据重排
第一轮排序:
申请32K空间作为重排的缓存,对这32K缓存,只用到其中的24K。数据重排的程序由汇编指令设计,为了提高效率,存取数据同时进行。先取数据至寄存器,存的时候以需要的顺序从寄存器读出,这样将数据存至缓存的时候,就已经重排好了。存完24K数据(每段取8K)后,再将数据搬回,将原数据覆盖,这一过程如图7。
经过第一轮重排后,数据分布规律如图8所示。
经过第一轮重排后,每段数据的首地址如图9所示。
可见,经过第一轮重排后,数据虽然得到了调整,但没有达到图6所示的顺序,还要经过第二轮重排,才能完成整个排序。
第二轮排序:
第二轮排序就是对图8的12个数据段进行交换,直至达到图6的顺序。交换时以整个数据段进行,第二轮排序的交换顺序如图10所示。
第二轮排序时,每次交换的2个数据段的首地址见表3。
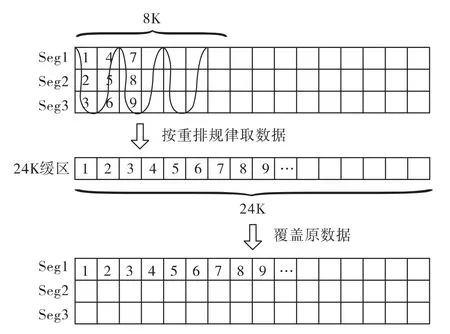
图7 第一轮重排示意图
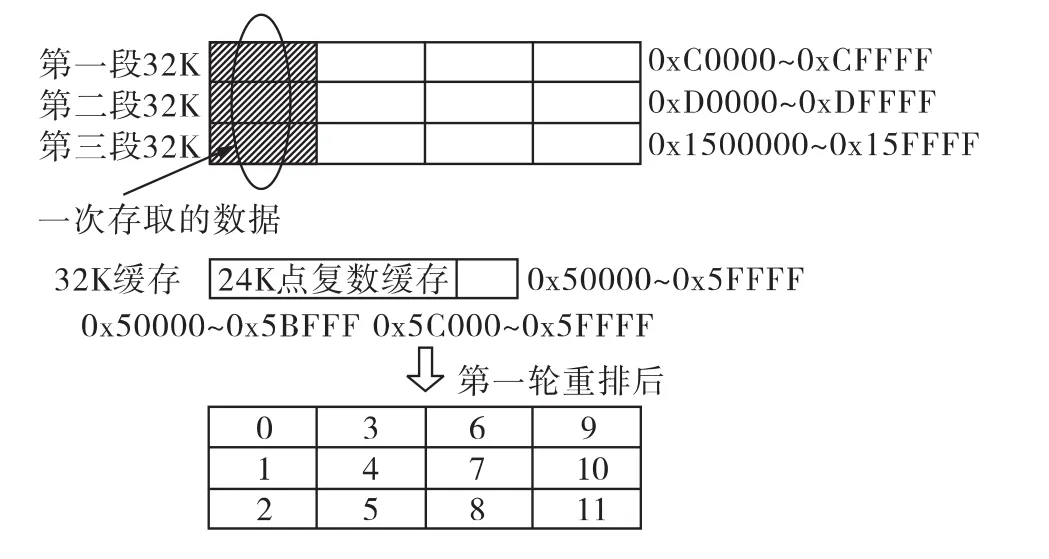
图8 第一轮重排后的数据分布
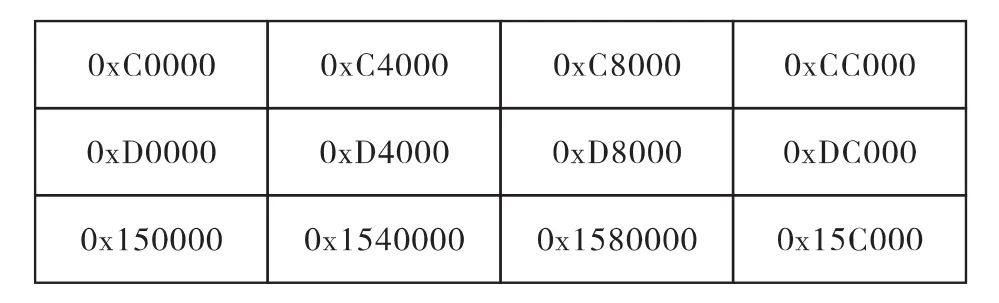
图9 第一轮重排后每段数据的首地址

图10 第二轮排序数据交换过程
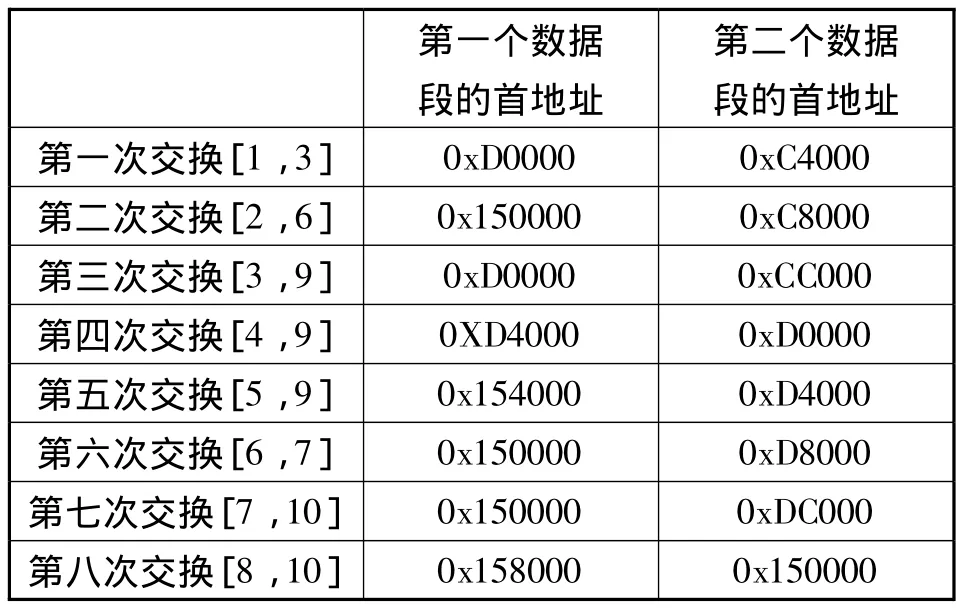
表3 第二轮排序时每次交换的2个数据段的首地址
至此,经过第二轮排序以后,数据在内存中的顺序就达到了期望的顺序,即完成了整个排序,从而完成了整个FFT变换。
对于大点数IFFT,可以在FFT的基础上实现,步骤如图11所示。

图11 大点数IFFT实现步骤
运行时间统计:在工程实现时,96K点复数FFT模块由四个函数组成:a.对每列数据做3点DFT并乘以中间旋转因子的函数DFT_3point_multMidT-wid.asm;b.对每行做32K点FFT的函数bw_cvfft_c.asm,该函数为通用的参数化FFT模块;c.第一轮排序函数ReArrange_dat_1stRound.asm;d.第二轮排序函数ReArrange_dat_2ndRound.asm。当ADSPTS201的核时钟运行于480MHz时,每个函数模块的运行时间统计见表4。

表4 函数运行时间统计
可见运行完96K点复数FFT需要的时间为:1.66+1.6*3+0.35+0.41=7.22ms。经测试,做完96K点频域脉压并对结果求模取对数,共计用时16.7ms。可见,这种处理大点数FFT的方法不仅解决了内存需求量大的问题,而且函数模块具有较好的实时性。
4 结束语
针对雷达信号处理遇到的大时宽脉压问题,给出了大点数FFT的变换方法。该方法大大降低了因存储旋转因子对内存的需求,在不与外部存储器交换数据的情况下,能够快速完成FFT变换。文章首先介绍了大点数FFT变换的数学原理,然后以96K点为例,阐述了其在通用处理器ADSP-TS201上的实现过程,为工程上实现其它点数的大点数FFT提供了有益的借鉴。
[1]丁玉美,高西全.数字信号处理[M].西安:西安电子科技大学出版社,2000:68-77.
[2]苏涛,庄德靖.大点数FFT算法的改进及其实现[J]. 现代雷达,2005,27(7):23-26.
[3]王晓君,龙腾,周希元.二维级联流水结构大点数FFT运算器实现研究[J].无线电工程,2010,40(11):19-22.
[4] 刘书明,罗勇江.ADSP TS20XS系列DSP原理与应用设计[M].北京:电子工业出版社,2007:115-118.

