一种简易制导火箭弹的弹目偏差研究
毕 进 王 乐 陈国际
(西安电子工程研究所 西安 710100)
0 引言
近几十年来多次战争表明,现代战争的主题是空袭与反空袭[1],这就显得防空系统越来越重要,但是由于现代来袭武器系统的不断改进,来袭武器平台投射距离越来越远,来袭武器速度越来越快,智能化越来越高,传统的导弹—火炮防空系统[2]应对这一变化效果不佳,为了应对这种变化,一种新型的简易制导火箭弹防空体系的出现迫在眉睫。
火箭弹弹道修正是在不破坏原弹的结构及基本性能的基础上,通过配备制导或控制组件,将无控火箭弹转化为简易制导火箭弹,在成本提高不多的情况下提高火箭弹的精度和密集度。采用制导火箭技术实现防空火箭炮的制导化,将是未来防空发展的一个重要方向。
1 简易制导火箭弹工作基本过程
工作原理可概括如下:
a.来袭目标的弹道数据分析。搜索雷达发现来袭目标,跟踪雷达立即跟踪来袭目标,实时测量出来袭目标的速度、方位、高度等目标诸元,并对目标信息进行滤波处理,实时解算来袭目标的轨迹。
b.简易制导火箭弹[3]弹道数据分析。根据来袭目标的轨迹发射火箭弹打击目标,并且实时跟踪发射的火箭弹,进行箭弹弹道解算和弹道预测,实时解算来袭目标弹道和火箭弹弹道误差,为末端修正提高数据依据。
c.合理选择和灵活运用外弹道模型,利用火控计算机得到较为精确的理论弹道数据作为弹道修正的依据,然后和雷达测得的信息相比较,计算该偏差,依据该偏差对理论弹道数据进行修正,然后由地面通过一定方式发送修正指令给简易制导弹箭。
d.火弹箭上接收机接收到修正指令后,由弹载计算机或者火控计算机根据偏差信息和弹上装置给出的信息,解算并发送指令,在火弹箭飞行的某个时刻或某几个时刻通过弹上修正机构执行对射程和方位的修正。
由末端修正箭弹的原理可知,它与无控箭弹相比主要还包括弹道探测系统,弹道偏差解算系统和弹道控制系统。在原理上克服了无控火箭弹有了弹道偏差而不能纠正的缺点,从而使弹丸的命中精度大幅度提高。
2 龙格-库塔法对弹箭质心运动方程的解算
火箭弹具有火箭发动机,发动机通过含有能量的物质的燃烧和喷出产生强大的推力,使火箭弹前进。火箭弹用定向器发射,发动机工作期间的弹道称为火箭弹主动段,即为图1中的OK段;发动机熄火后的弹道称为被动段,即为图中的K点以后的弹道。被动段内的火箭弹实际上与普通炮弹是一样的,因此可以用普通的炮弹外弹道理论分析火箭弹被动段的弹道特性。这样我们可以根据被动段开始的弹箭诸元,对弹道进行外推,进而计算与目标的偏差。末端修正火箭弹正是在被动段对火箭弹进行修正减小偏差,达到命中目标的目的。
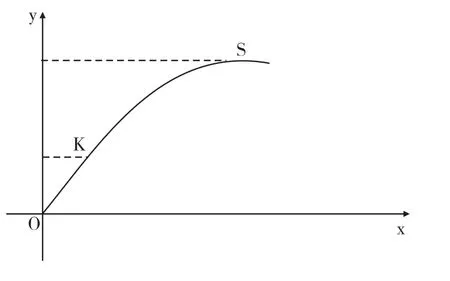
图1 火箭弹全弹道示意图(OK为主动段,K点后为被动段,S为最高点)
直角坐标系的外弹道质心运动系统仿真,就是在外弹道质心运动系统内,以直角坐标系的弹丸质心运动方程组为数学模型,按照系统仿真的流程对弹丸在空气中的运动进行仿真研究。这里先写出龙格-库塔法的一阶迭代系数,即:
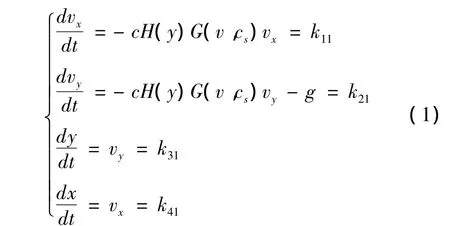
将一阶迭代系数带入四阶龙格-库塔法[4]公式中可得:
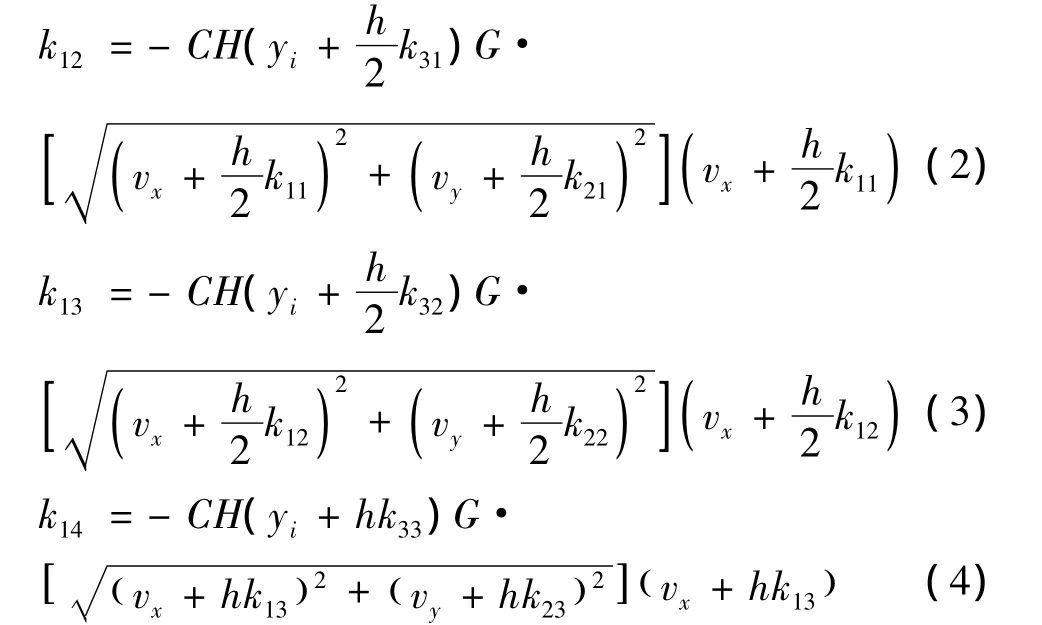
同理可以得出k22、k23…k43、k44,即可由公式:
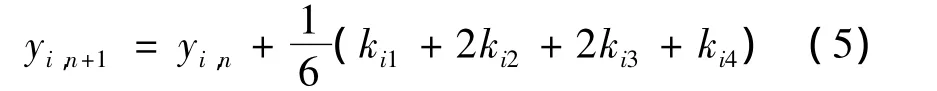
得到下一个时刻弹道诸元。弹箭质心运动方程可以揭示弹箭运动的基本规律和特性,并且可用于计算弹道,但并不特别严格和准确。基于弹箭质心运动方程,用龙格-库塔法解算的弹道曲线,在一定程度上反映了弹箭的运动过程以及倾角变化过程,对我们以后工作进一步研究火箭弹被动段的运动以及实际的弹道曲线很有帮助。
3 弹目误差解算
目标方程和弹道方程在同一时间轴下解算,计算得出极小值就是弹目命中最小误差,为火箭弹是否修正以及修正量大小做好数据准备。在直角坐标系下目标方程组可以表示为:

雷达跟踪目标轨迹并且进行轨迹预测,雷达采样间隔为Δt=0.2s,则目标第n+1点的预测坐标可以表示为:
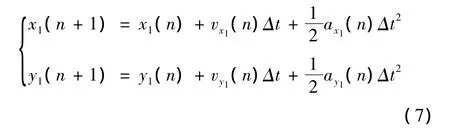
将方程组表示为矩阵坐标的形式为:
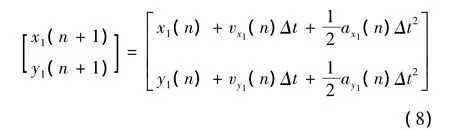
直角坐标系下火箭弹被动段弹道方程为:
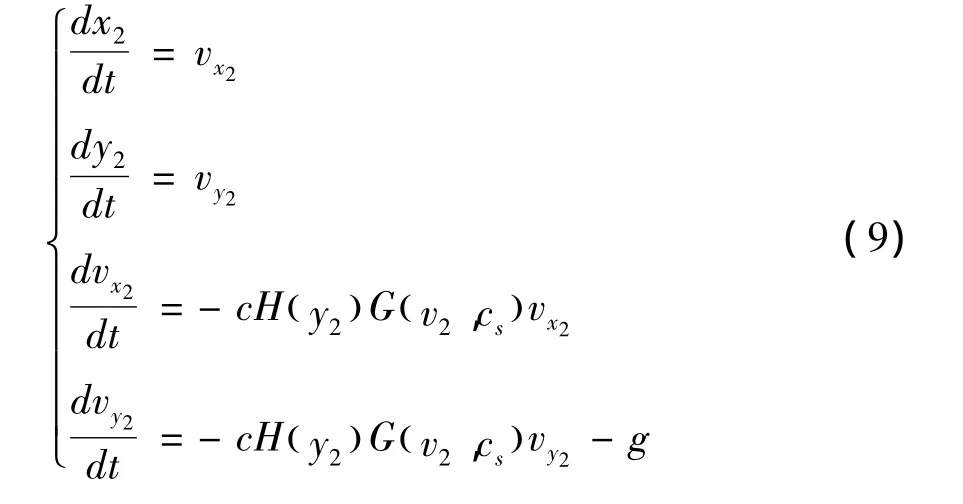
对于大多数实际问题,四阶龙格-库塔法已经可以满足精度要求,误差正比于时间步长h的5次方,这里用龙格-库塔法解算火箭弹被动段弹道方程,可以得到火箭弹被动段弹道预测点的坐标递推为:
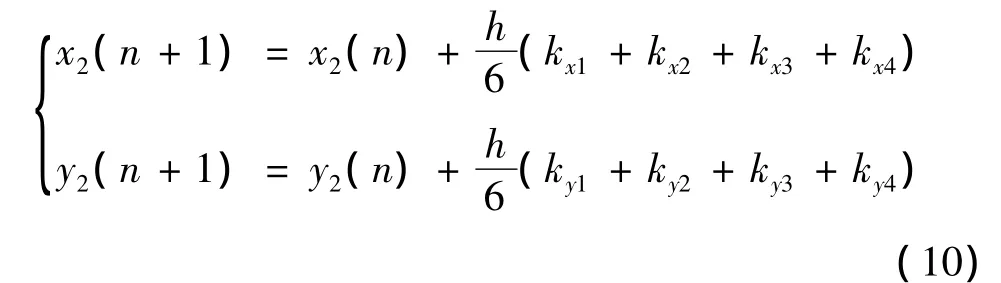
式中时间步长h的取值同雷达跟踪目标采样点的时间间隔相同,即 h=0.2s,kx1… kx4,ky1…ky4递推公式可由式(1)~式(5)递推得到。
式(10)用矩阵形式表示可得:
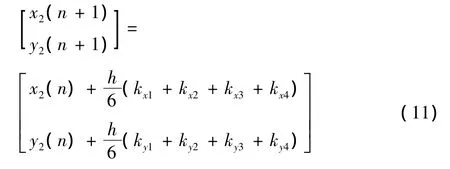
火箭弹命中目标的误差为在相同时间轴上相同时间点预测的火箭弹坐标和目标坐标的距离。令火箭弹坐标为点A,目标坐标为点B,则预测命中误差大小
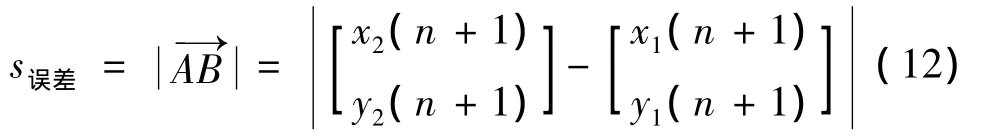
式(8)和式(11)代入式(12),可以得到预测命中误差大小是关于n的函数。求最小误差问题转化为求误差函数的极小值问题,其中自变量n只能取正整数。
假设来袭目标在50km处被搜索雷达发现,并且跟踪雷达跟踪目标,发现来袭目标为匀速直线运动,速度为v=500m/s。火控计算机解算出目标预测轨迹,并且根据预测轨迹发射火箭弹。当来袭目标飞行到30km处时,火箭弹进入被动段。此后进行弹道和目标轨迹的实时预测,在同一时间轴下不断解算火箭弹和来袭目标的命中误差。所以火箭弹进入被动段时间点为目标轨迹方程和弹道轨迹方程的积分初始点。t=0时,来袭目标方程积分初始条件:
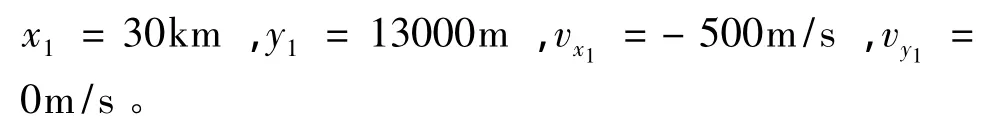
火箭弹弹道方程积分初始条件为:
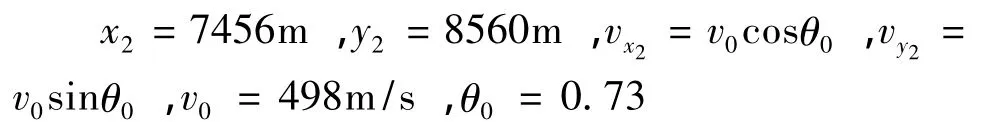
式中v0为火箭弹被动段初始速度,θ0为火箭弹被动段初始射角。
在初始条件已知情况下,预测的目标轨迹点为:
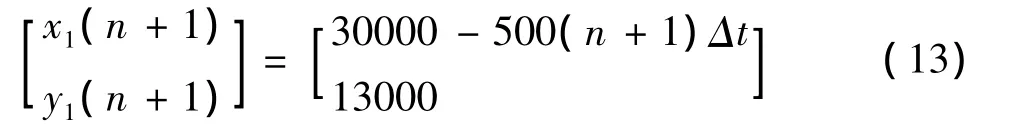
式中 Δt=0.2s,n 为正整数。
式(11)和式(13)带入式(12)中,可以得到匀速直线运动目标来袭时的预测弹目误差表示式:

可以用MATLAB仿真计算出s误差的极小值。仿真结果如图2和图3所示。图中来袭目标为匀速直线运动,火箭弹对其进行拦截。初步瞄准后发射火箭弹,当火箭弹进入被动段时记为时间零点,此时实时预测弹道轨迹和目标轨迹,并计算预测误差大小。
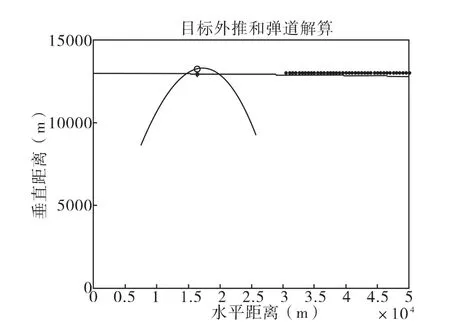
图2 火箭弹被动段弹道外推及目标预测仿真图
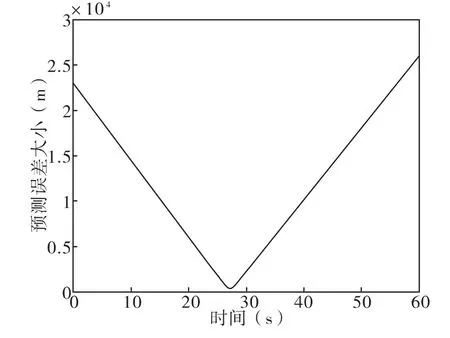
图3 解算火箭弹命中目标的误差
图3中的蓝色曲线为以火箭弹被动段起始点为弹道解算初始点,进行的弹道轨迹预测,黑色点汇集成的线为假定来袭目标的位置坐标形成的轨迹,红色线条为用卡尔曼滤波对目标位置的跟踪以及外推。当火箭弹结束主动段进入被动段时,开始进行弹道解算外推,同时根据判定出的目标模型,运用卡尔曼滤波进行目标轨迹的预测外推,实时解算火箭弹[5]和目标的误差。并且判定是否启用弹道修正模块,进行弹道的修正。随着时间的推移,火箭弹和目标越来越接近,不断的根据目标和火箭弹的实际状态进行目标轨迹预测和弹道预测,预测的命中误差越来越小。当到某一误差范围内,进行弹道修正,使修正后的火箭弹和目标在未来的某一时刻到达同一点,即火箭弹命中目标;当目标发生机动变化,同样根据变化后目标的一段实际轨迹,对目标进行判定和预测,然后进行弹道修正,使其命中目标。如图4所示曲线,在t=0s时解算出的火箭弹命中目标的误差,预测当t=27.2s时,火箭弹与来袭目标的误差最小,为s误差=300m。即在图3中,预计火箭弹到达红色小圈位置,运动目标到达绿色小点位置。这就为制导火箭弹进行命中运动目标前的末端修正提供修正依据。
4 结束语
这里用简易的弹道方程和假设的简单运动目标,只是说明实现末端修正火箭防空的技术过程中的误差解算,为后续进行实际的火箭弹防空做好理论准备。实际过程要求更加复杂、更加切合实际的弹道方程,并且目标的运动状态具有更强的机动性,这就要求有更加优秀的弹道解算和目标跟踪预测能力。制导火箭弹用于防空是现在全世界共同研究的课题,而本文是在全面开展防空新思路的探索的背景下提出的基于末端修正的火箭防空技术研究,课题的探索性十分显著,研究成果开创火箭弹闭环测量修正防空的基本理论基础。
[1]徐国诚.高技术空袭与防空[M].北京:国防大学出版社,2000.
[2]刘浩.弹箭炮三结合武器系统在近程防空反导中的应用[J].四川兵工学报,2009,30(8):41-43.
[3]葛贤坤,黄长强等.末段修正火箭弹简易脉冲修正技术[J].火力与指挥控制,2008,33(5):148-150.
[4]李丹.四阶龙格-库塔法在火控解算中的应用[J]. 微计算机信息,2011,27(3):192-193.
[5]慈颖.高精度实时弹道预报方法研究[J].飞行器测控学报,2010,29(5):80-84.

