雷达目标最大信号法测角精度研究

徐振海，王罗胜斌，熊子源，王 伟

(国防科技大学电子信息系统复杂电磁环境效应国家重点实验室，湖南 长沙 410073)

0 引言

在“雷达原理”课程教学中，目标角度测量是最基本、最重要的内容之一。雷达粗略测角通常采用最大信号法，其核心思想是:天线扫略目标过程中，目标回波受天线方向图调制，回波幅度最大时刻的天线波束的指向角即目标角度，图1给出了最大信号法的原理示意图。

关于最大信号法的测量精度，经典教材[1]给出的结论是:“该方法测角精度不高，约为波束宽度的1/5左右”;经典雷达专著[2]的结论是:“在目标可靠检测所要求的典型信噪比条件下，测角精度大约为波束宽度的1/4到1/10”。这些结论过于笼统，学生在学习时对该知识点提出了较多疑问。比如，影响测角精度的因素有哪些?测角精度与SNR的关系如何?测角精度与角度采样间隔的关系如何?而有关的文献资料以及雷达手册却没有给出定性解释和定量证明[2-4]。

图1 最大信号法测角原理示意图

最大信号法原理的实现有多种方法，最直接的方法就是选取测量回波序列的峰值点对应的角度即目标角度，该方法简称峰值法;还可以通过对测量回波序列进行曲线拟合，根据拟合函数解析求出峰值点，该方法简称拟合法。然而这两种具体实现方法性能是否相同?孰优孰劣?这些问题也均未见相关文献报道。

鉴于此，笔者对该知识点进行了深入的研究。首先，根据最大信号法原理建立了天线接收回波模型;然后详细给出峰值法和拟合法的测角公式;最后通过仿真研究这两种方法的测角性能，并得出结论。

1 接收回波模型

根据最大信号法原理，不失一般性，假设雷达天线方向图为辛克函数，归一化方向图为

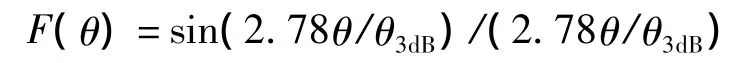
式中，θ3dB为3dB波束宽度。

假设上式的目标角度为0，天线匀速旋转，接收回波受天线方向图调制，也等效于雷达天线静止，而目标在等间隔步进。假定在3dB波束宽度内步进角度间隔为Δθ=θ3dB/2M，在主瓣内共有2M+1个脉冲。测量序号记为m=(-M，…，0，…M)，第m次测量对应的角度为θm=mΔθ，雷达接收的复信号为

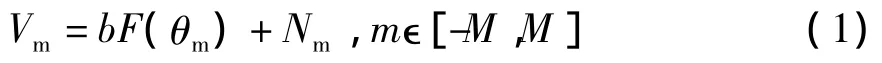
其中，b为信号幅度，不失一般性假设为实数;Nm=rm+jim为接收机热噪声，服从零均值复高斯分布，方差为σ2，其实部rm和虚部im均服从零均值实高斯分布，方差均为σ2/2。雷达接收信号经过检波得到信号包络为

2 最大信号法测角

2.1 峰值法

根据峰值法思想，目标角度估计可表示为

宗教对文学的影响，属于比较文学的跨学科研究的范畴。在文学产生和发展的过程中，宗教曾经起过重要作用；宗教会对作家的世界观发生影响，进而影响到文学作品的思想内容，有些重要的宗教经典，如《圣经》，本身就是文学作品，或者取自文学作品。[1]274-275

由于噪声的影响，测量序列中每个值都有可能取得最大值，只是概率不同。设第m次测量值达到全局最大的概率为Pm，显然天线主瓣中心位置处取得最大值的概率P0最大;由于天线方向图是对称的，概率分布也具有对称性，即Pm=P-m。其理论解如下:

其中，z为2M维复随机向量，服从零均值协方差矩阵为C的正态分布。图2给出了不同SNR条件下概率分布图(主瓣内角度间隔为0.1倍波束宽度)。可以看出:随着SNR的提高，概率分布越来越集中，预示着测量精度的提高。

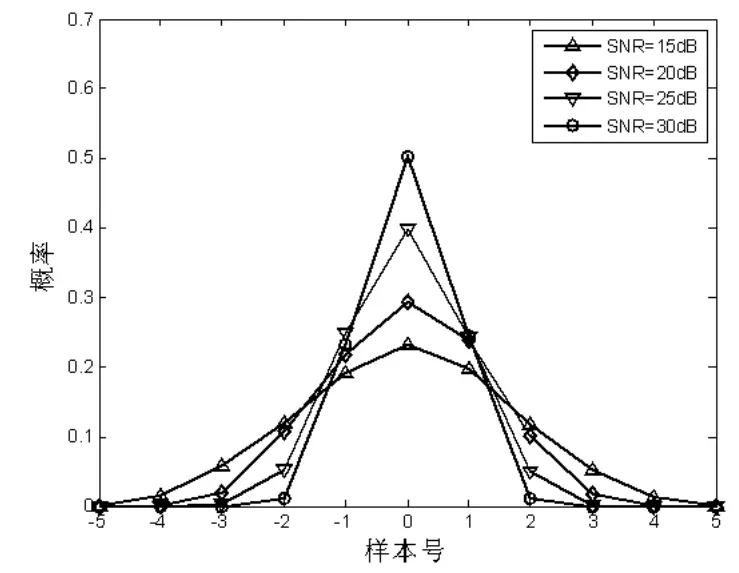
图2 峰值点概率分布列

根据概率分布可得峰值法估计的均值为

因此，峰值法是无偏估计。峰值法估计的均方差为

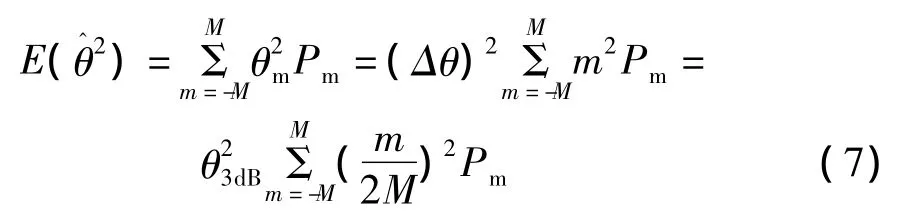
2.2 拟合法

根据拟合法思想，对天线主瓣内测量到的幅度序列用二次函数(即抛物线)来进行拟合可得

拟合得到的抛物线峰值即目标角度的估计，即:

3 测角精度仿真

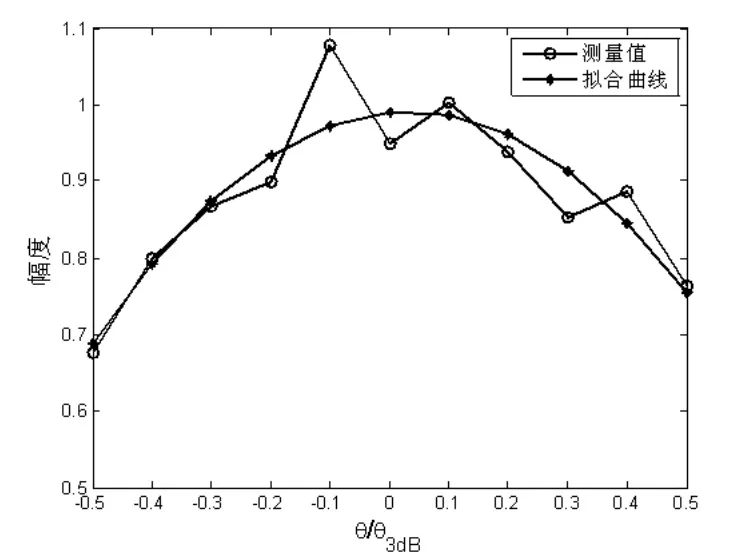
图3 拟合法示意图

本节通过仿真研究峰值法和拟合法测角精度与SNR及样本数之间的关系，SNR定义为回波信号功率与热噪声方差之比，即:SNR=b2/σ2。估计精度采用归一化均方根误差来表示，蒙特卡洛仿真次数为1000。

3.1 测角精度与SNR的关系

在本仿真中，设定主瓣内采样间隔为0.1θ3dB，图4给出了峰值法、拟合法测角精度与SNR的关系曲线。

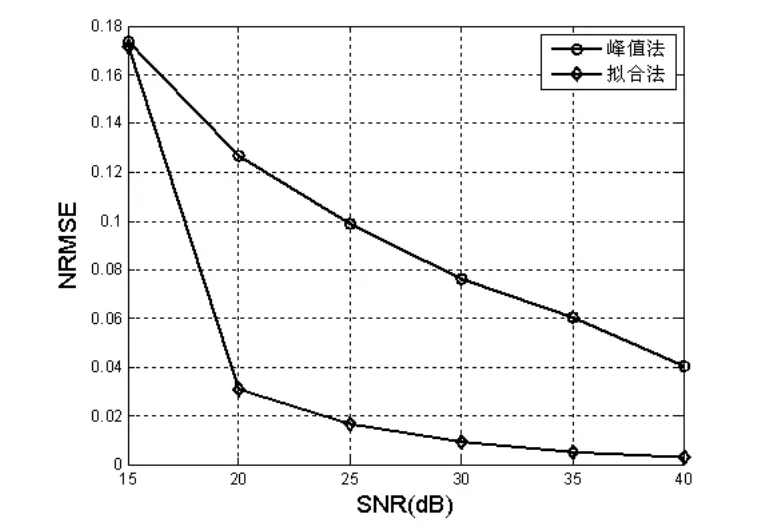
图4 估计精度与SNR的关系

可以看出:当典型SNR(15dB～25dB)条件下，峰值法测角误差大约在1/5到1/10波束宽度，与文献[2]的结论是吻合的，随着SNR的增加测角精度继续提高;而拟合法测角性能整体优于峰值法，并且要高一个数量级，其原因就是拟合处理抑制了噪声的影响，可以实现高精度测角。

3.2 测角精度与样本数的关系

在本仿真中，图5给出了SNR为25dB时的峰值法、拟合法测角精度与样本数的关系曲线。

可以看出:随着样本数的增加，两种方法的测量误差总体上是下降的，但是下降的趋势比较缓慢。可见，想通过提高雷达重频来换取测量精度的改善是不经济的，在实际应用中只要在主瓣内有几个采样值即可。

图5 估计精度与样本的关系

4 结语

本文详细深入研究了雷达目标最大信号法测角精度问题，峰值法测角精度与经典文献的结论是吻合的，拟合法测角精度要比峰值法高一个数量级;另外，试图通过减小主瓣内角度间隔来换取测角精度的改善是不经济的。本文仅从雷达接收的角度展开研究，如果考虑收发过程，则需要将天线的归一化方向图用其平方代替，并且3dB宽度要根据双程方向图来定义，但是不影响研究结论的正确性。另外，本文是针对雷达目标角度测量而展开的，实际上最大信号法原理对于快时间域距离测量和多普勒域径向速度测量都是相通的，只要将角度域天线方向图的概念拓展到时域相关函数和频域滤波器函数即可。

通过雷达最大信号法测角精度的定量证明可加深学生对该知识点的理解，使学生能够在教学中发现问题，并且利用已有的数学知识和软件技能开展研究，这正是开展研究型教学活动的本质要求。

[1]丁鹭飞，耿富录，陈建春，雷达原理(第四版)，北京:电子工业出版社，2011.05，361-362

[2]斯科尔尼克，雷达系统导论(第三版)，北京:电子工业出版社，2006.07，236

[3]王小谟，张光义，等，雷达与探测(第二版)，北京:国防工业出版社，2008.07，18

[4]斯科尔尼克，雷达手册(第二版)，北京:电子工业出版社，2003.07，9-10