波浪与开孔沉箱相互作用的CLEAR⁃VOF数值模拟
邢飞,孙大鹏,夏志盛,吴浩
(大连理工大学海岸和近海工程国家重点实验室,大连116023)
波浪与开孔沉箱相互作用的CLEAR⁃VOF数值模拟
邢飞,孙大鹏,夏志盛,吴浩
(大连理工大学海岸和近海工程国家重点实验室,大连116023)
摘要:文章利用三步有限元方法离散Navier⁃Stokes方程,并借助CLEAR⁃VOF方法、大涡模拟方法追踪水体自由表面和模拟湍流效应,建立了二维数值波浪水槽。籍此研究了规则波作用下开孔沉箱的反射率和波浪总水平力,并与物模试验结果和其他学者的数模结果以及工程实例进行了对比,吻合良好,为波浪与开孔沉箱相互作用问题的研究探索了一种新的数值模式。
关键词:三步有限元;CLEAR⁃VOF方法;开孔沉箱;反射率;总水平力比
自1961年Jarlan提出开孔沉箱以来,国内外大量采用了这种形式的防波堤来减小波浪的反射及其对建筑物的作用力。对于波浪与开孔沉箱相互作用的研究,目前主要有物模试验和数值模拟两种途径,陈雪峰、李玉成等[1-2]利用物理模型试验研究了单层和双层开孔沉箱在规则波和不规则波作用下的反射率、水平力及点压力分布;张玉彬、孙大鹏等[3]利用物理模型试验研究了明基床上开孔沉箱在规则波作用下的受力情况;施晓迪等[4]利用物理模型试验研究了开孔率和开孔范围对开孔沉箱消浪性能的影响;朱大同[5]得出了波浪与开孔沉箱相互作用的反射率的严格封闭解析公式;陈雪峰[2]采用改进的VOF方法结合k⁃ε模型建立二维数值波浪水槽,完成了线性规则波和不规则波与单层开孔沉箱相互作用的数值模拟。目前,对于波浪与开孔沉箱相互作用的物模试验成果较为丰富,但是数值模拟研究成果相对较少,其中,时域内准确地完成对自由水面的追踪,是建立波浪与开孔沉箱相互作用数值模式过程中的难点问题之一。
Ashgriz等[6]于2004年提出了CLEAR⁃VOF(A combination of a Computational Lagrangian⁃Eulerian Advec⁃tion Remap and the Volume of the Fluid method)自由表面重构技术,其精度较高且适用于任意多边形网格。本文借助CLEAR⁃VOF方法追踪水体自由表面,建立了波浪与开孔沉箱相互作用的三步有限元数值模式。并分析了规则波作用下开孔沉箱反射率和波浪总水平力的计算结果,为研究波浪与开孔沉箱相互作用探索了一种新的数值模式。
1 数值计算方法
1.1控制方程及其离散
基本控制方程为二维不可压缩粘性流体的连续性方程和Naiver⁃Stokes方程

由于直接进行湍流模拟在现有的计算条件下难以实现,本文采用大涡模拟的方式模拟湍流效应,通过滤波的手段将实际流场分解为大尺度和小尺度的涡流场,对其中大尺度的流场物理量进行直接数值模拟,小尺度的物理量通过模型化的手段加以反应。经滤波处理并引入广义Boussinesq涡粘假设对控制方程进行封闭之后得到

式中:有效粘性系数νe为运动粘性系数ν与湍流粘性系数vt之和。
三步有限元方法比传统的有限元方法精度更高,数值实现过程相对简单且高效。对Taylor时间展开取三阶精度,将每个Δt时间步长分为Δt/3,Δt/2和Δt三步来完成,其基本思想如下

本文计算中,三步有限元展开N⁃S方程的形式为
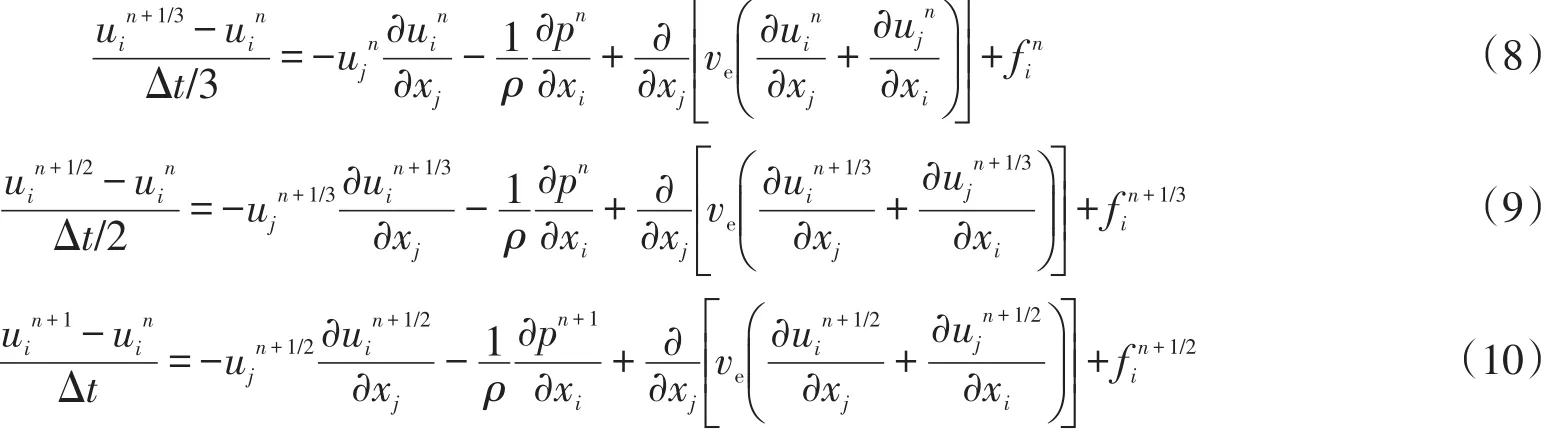
在Δt/3步,利用式(8)由上一时刻求出的速度un和压力pn求出该时刻的速度un+1/3;在Δt/2步,由式(9)易求得该时刻的速度un+1/2;而在Δt步,由于式(10)中存在未知量pn+1,因此引入压力泊松方程[7-8]

至此,方程组封闭。可采用Galerkin加权余量法进行离散求解。
1.2CLEAR⁃VOF追踪流体自由表面
与传统的基于有限差分方法提出的VOF方法不同,CLEAR⁃VOF方法不需要通过求解输运方程来更新F函数,而是通过欧拉网格节点拉格朗日运动和计算几何手段实现。在非结构化欧拉网格计算区域中,当F=0时,单元内无水,不存在流体多边形;当F=1时,流体多边形与网格重合,流体多边形的顶点即网格单元节点;当0<F<1时,流体多边形的顶点包括网格单元节点和自由表面界线与网格边线的交点。
以图1为例,图中实线为计算区域的不规则欧拉网格,对于某时刻t,各单元节点的速度已知,网格边线上任意点的速度可由插值方法求出,单元a-b-c-d-e为自由表面单元(其中e-d为自由表面界线);根据拉格朗日思想计算流体多边形的运动,则t+Δt时刻,该单元运动至a1-b1-c1-d1-e1,初步实现了流体向周边网格的输运;通过复杂的计算几何方法得出t+Δt时刻下流体多边形留在母单元内的面积和进入母单元相邻单元的面积,对所有网格单元进行计算,得到新时刻的F函数、自由表面界线和各流体多边形的顶点速度,并将此作为下一时刻的已知条件循环计算,直到计算结束。

图1CLEAR⁃VOF方法中的流体多边形示例Fig.1Sketch of fluid polygon of CLEAR⁃VOF
2 数值波浪水槽的建立
2.1线性波浪模拟
利用上述数值计算方法,如图2所示建立二维数值波浪水槽,水槽前端为造波区,为得到理想的线性规则波,采用Dong C M等[9]提出的无反射造波理论,理论波面η和造波板运动速度U分别为
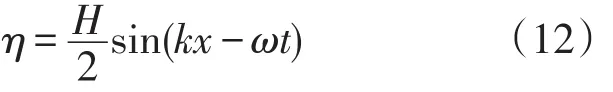
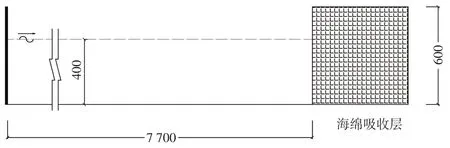
图2 波浪数值水槽模拟计算域Fig.2Computational domain for numerical flume

式中:H为理论波高;k为波数;ω为频率;d为水槽水深;ηRe为造波板前实际波面高程;ηTh为造波板前理论波面高程。
水槽末端安放由Larsen J等[10]提出的海绵吸收层消波边界,在海绵吸收层内按下式对速度进行衰减

式中:us为海绵吸收层内单元节点的速度;μ(x)为衰减函数;α为常系数,本文取1.1;Ls为网格单元中心到海绵吸收层末端边界的距离;λ为海绵吸收层的厚度,本文取最大波长的1.5倍,为3.6 m。
数值水槽工作区长7.7 m,高0.6 m,水深d为0.4 m,波高H取0.10 m,0.12 m,周期T取0.86 s,1.0 s,1.2 s,1.4 s,计有8种波要素组合。波浪传播稳定后,各工况的线性规则波浪与理论解吻合良好。限于篇幅,本文以波高0.10 m、周期1.0 s工况为例给出了水槽工作区末端位置的波高历时曲线,如图3所示,图中实线表示理论值,圆圈表示本文计算值。

图4 二维数值波浪水槽中开孔沉箱的布置图Fig.4Sketch of perforated caisson in two⁃dimensional numerical flume
2.2开孔沉箱结构物的设置
水槽工作区末端安放开孔沉箱如图4-a所示,开孔沉箱的开孔板尺寸如图4-b所示。宽68 cm,高40 cm的开孔面上布置大小相同的高3.8 cm,宽14.2 cm的12个孔,开孔率为23.8%,消浪室宽度为0.3 m,消浪室内的水深为0.2 m。
数值模拟过程中采集距开孔板2.5 m、2.9 m和3.5 m处的波面时间过程信息用以计算分析反射率。
在数值计算的过程中,将开孔沉箱的后实体直墙和开孔板的固壁部分定义为自由滑移边界(全反射边界),即边界法向速度设置为u=0。
3 数值计算结果及分析
开孔沉箱的消浪效果常用反射率和水平力来加以评价。为验证本文数值模式研究波浪与开孔沉箱相互作用的适用性和准确性,将本文计算结果与物理模型试验结果(物理模型试验在大连理工大学海岸和近海工程国家重点实验室的波流水槽进行,数值试验和物模试验的结构物尺寸、试验波要素等保持一致)[2]、陈雪峰[2]改进的VOF方法结合k⁃ε模型的数值计算结果进行对比验证。
3.1反射率的比较
反射率按照合田良实[11]提出的两点法来计算。陈雪峰等[2]通过分析物理模型试验数据,得到了反射率Kr与入射波长L、水深d、消浪室宽度B和开孔率α之间的经验关系

图5-a、图5-b分别给出了波高为0.10 m和0.12 m工况下反射率的比较。其中横坐标为波长,纵坐标为反射率;实线表示经验公式(16)的结果,圆点表示本文的数值计算结果,三角形点表示陈雪峰的数值计算结果。由图5可知,本文数模的反射率结果比陈雪峰数模结果略小,但与式(16)吻合较好。

图5 反射率的比较Fig.5Comparison of reflection coefficient
3.2水平力的比较
以F1/F0作为开孔沉箱总水平力的分析指标,其中开孔沉箱所受水平总力F1为开孔板的迎浪面、背浪面及后实体墙的合力,实体沉箱所受水平总力F0为其迎浪面所受水平力。陈雪峰等[2]通过分析物理模型试验数据,得到了波峰(谷)总水平力比F1/F0与入射波长L、波高H、水深d、消浪室宽度B和开孔率α之间的经验关系

图6、图7分别给出了波高为0.10 m和0.12 m工况下(a)波峰总水平力比的比较和(b)波谷总水平力比的比较。其中横坐标为波长,纵坐标为力比;实线表示经验公式(17)或经验公式(18)的结果,圆点表示本文的数值计算结果,三角形点表示陈雪峰[2]的数值计算结果。由图可知,本文计算的波峰(谷)总水平力与陈雪峰数模结果以及式(17)和式(18)吻合较好且规律性明显。

图6 波峰(谷)总水平力比的比较(h=0.10 m)Fig.6Comparison of ratio of the total horizontal forces(h=0.10 m)

图7 波峰(谷)总水平力比的比较(h=0.12 m)Fig.7Comparison of ratio of the total horizontal forces(h=0.12 m)
4 工程实例验证
大连港大窑湾港区#11~#16泊位的规划设计中,采用图8所示的开孔沉箱。静水水深14.44 m,沉箱迎浪面规则分布16个方形开孔,沉箱内部以碎石紧密填充。本文以该工程为例,选取未发生越浪的工况进行比较,由于原始资料数据有限,本文仅给出实际尺度开孔沉箱结构波浪反射系数的数值验证。
表1给出了不同工况规则波作用下实际尺度开孔沉箱反射率的本文计算值和设计值的比较。由表1可知,本文计算结果与实际工程反射率吻合良好,说明本文所建立的数值模式可适用于开孔沉箱结构的工程设计应用。
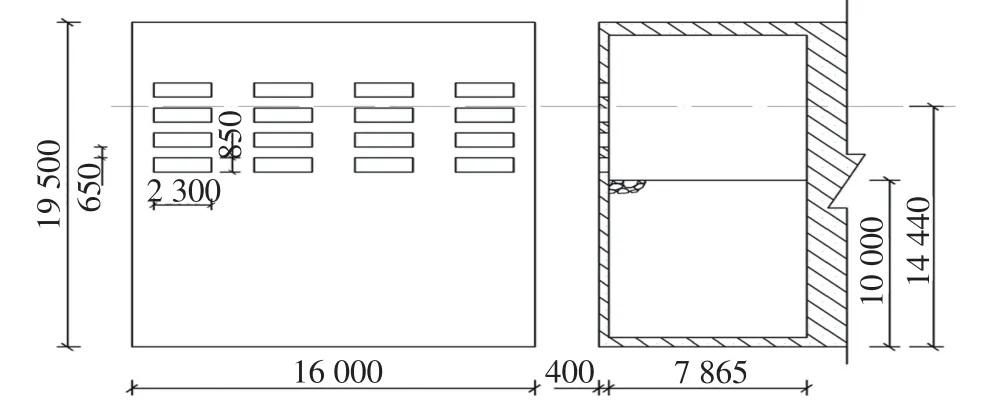
图8 开孔沉箱防波堤工程实例Fig.8Engineering project of perforated caisson

表1 实际尺度开孔沉箱反射率的比较Tab.1Comparison of reflection coefficient of engineering project
5 结语
本文基于Navier⁃Stokes方程,借助大涡模拟方法模拟湍流效应,并成功地实现CLEAR⁃VOF追踪水体自由表面,建立了波浪与开孔沉箱相互作用的三步有限元数值模式。进而在数值波浪水槽中对开孔沉箱前的波浪反射率和沉箱所受波浪水平力进行了数值模拟,本文数值计算结果与物理模型试验结果[2]吻合较好且规律性明显,并且进行了实际尺度开孔沉箱防波堤的数值验证,表明本文开发的波浪数值模式对于开孔沉箱的波浪反射率和波浪力数值模拟具有良好的适用性和准确性,为该问题的研究探索了一种新的数值模式。
参考文献:
[1]陈雪峰,李玉成,孙大鹏,等.波浪与开孔沉箱作用的实验研究[J].中国海洋平台,2001,16(5):1-6. CHEN X F,LI Y C,SUN D P,et al.An experimental study of wave acting on perforated caisson[J].China Offshore Platform,2001,16(5):1-6.
[2]陈雪峰.波浪与开孔沉箱的相互作用[D].大连:大连理工大学,2003.
[3]张玉彬,孙大鹏,夏志盛,等.明基床上开孔沉箱水平力极值对应的垂直力分析[J].中国海洋平台,2012(5):12. ZHANG Y B,SUN D P,XIA Z S,et al.Analysis on total vertical forces of perforated caisson sitting on rubble mound foundation while total horizontal forces reach its peak[J].China Offshore Platform,2012(5):12.
[4]施晓迪,琚烈红,冯卫兵,等.开孔沉箱消浪性能试验研究[J].水运工程,2011(3):4. SHI X D,JU L H,FENG W B,et al.Experimental research on wave attenuation effectiveness of perforated caission[J].Port& waterway engineering,2011(3):4.
[5]朱大同.开孔沉箱防波堤的波浪反射系数[C]//中国海洋工程学会.第十二届中国海岸工程学术讨论会论文集.北京:海洋出版社,2005.
[6]Ashgriz N,Barbat T,Wang G.A computational Lagrangian⁃Eulerian advection remap for free surface flows[J].International Jour⁃nal for Numerical Methods in Fluids,2004,44(1):1-32.
[7]吕林.海洋工程中小尺度物体的相关水动力数值计算[D].大连:大连理工大学,2006.
[8]孙英伟.直立堤前的破碎波流场特征及波浪力研究[D].大连:大连理工大学,2012.
[9]Dong C M,Huang C J.Generation and propagation of water waves in a two⁃dimensional numerical viscous wave flume[J].Journal of waterway,port,coastal,and ocean engineering,2004,130(3):143-153.
[10]Larsen J,Dancy H.Open boundaries in short wave simulations⁃a new approach[J].Coastal Engineering,1983,7(3):285-297.
[11]合田良实.港工建筑物的防浪设计(中译本)[M].北京:海洋出版社,1983.
全球最大波浪实验水槽首次实验成功
本刊从交通运输部天津水运工程科学研究院获悉,2014年7月29日,现今全球最大规模的大比尺波浪水槽成功进行了首次实验——新型双箱浮式防波堤结构稳定和消浪效果原型实验。该大型水动力实验中心大比尺波浪水槽长450 m、宽5 m、深8~12 m,能产生3.5 m的波浪和20 m3/s的水流,能进行1:5到1:1的大比尺模型试验,是目前世界上尺度最大、造波能力最强的波浪试验水槽。大型水动力实验中心将建设成为具有国际领先水平的中国水运工程科研创新平台。大比尺波浪水槽通过接近原型的实验研究,克服比尺效应,突破水运工程建设中涉及建筑物安全、生态环保、防灾减灾的水流、波浪、泥沙、地基、工程结构等基础理论技术制约,形成强大的自主创新能力。该次实验按照1∶1比尺进行了波高1.5 m的验证性实验和波高2.25 m的破坏性实验。(殷缶,梅深)
Biography:XING Fei(1990-),male,master student.
中图分类号:TV 139.2;O 242.1
文献标识码:A
文章编号:1005-8443(2014)05-0497-06
收稿日期:2013-12-27;修回日期:2014-02-27
基金项目:国家自然科学基金(51279027);国家自然科学基金(51221961)
作者简介:邢飞(1990-),男,山东省潍坊市人,硕士研究生,主要从事波浪与结构物相互作用的研究。
Numerical simulation of wave interaction with perforated caisson breakwaters by CLEAR⁃VOF method
XING Fei,SUN Da⁃peng,XIA Zhi⁃sheng,WU Hao
(State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116023,China)
Abstract:A two⁃dimensional numerical flume based on the Navier⁃Stokes equations which were discretized with a three⁃step finite element method was developed to simulate water wave problems.In this numerical model,large eddy simulation method was used to describe the turbulent effect and computational Lagrangian⁃Eulerian ad⁃vection remap and the volume of the fluid method(CLEAR⁃VOF)was used to advect free surfaces.The reflection coefficient of perforated caisson and the ratio of the total horizontal force acting on the perforated caisson to them acting on the solid caisson had been studied under linear regular waves by using this numerical method.Through the comparison with physical model test,numerical calculation of other scholars and engineering project,it can be known that the numerical method may be useful for studying wave interaction with perforated caisson breakwaters.
Key words:three⁃step finite element method;CLEAR⁃VOF;perforated caisson;reflection coefficient;total horizontal force
——缺陷度的算法研究

