圆筒形直线感应电动机性能的计算与分析

贾小龙，王庆贤，朱强化，马天海

(1.兰州交通大学，兰州730070;2.甘肃靖远第二发电有限公司，白银730600)

0 引 言

圆筒形直线感应电动机是基于电磁原理工作并提供大功率、高推力的主要执行元件。由于它不需要中间机械传动变换装置，就能直接产生连续单向或往复短行程的直线机械运动，因而在国民经济各个部门都获得了广泛的应用。从它的应用前景来看，圆筒形直线感应电动机将会拥有一个巨大的市场。圆筒形直线感应电动机由普通旋转感应电动机演变而来，即将旋转电动机沿径向剖开并将它拉直，就得到了扁平型直线感应电动机，再把扁平型直线感应电动机绕着与磁场移动方向平行的某中心线卷成一圆筒形，这样，就得到一种结构完全不同的圆筒形直线感应电动机。普通旋转感应电动机演变成圆筒形直线感应电动机，工作原理基本一样，但是由于结构的特殊性，使直线感应电动机的性能与旋转感应电动机相差很大。直线感应电动机由于其特有的边端效应，使得对其分析更为复杂［1－3］。本文采用有限元方法，对圆筒形直线感应电动机进行了分析，进而计算出其运行特性，并将理论计算与实验结果进行了比较。

1 模型的建立

本文针对一台长次级短初级的圆筒形直线感应电动机进行研究，基本参数如表1所示。

表1 电机的基本参数

建立一个适当的电机模型是研究电机特性和控制技术的基础。由于直线感应电动机特有的边端效应，使直线感应电动机和旋转电动机的数学模型有所不同。为建模分析的目的，作如下假设:

1)电机周向材质均匀，各过轴线的截面磁位值相同，因此可用二维轴对称分析对电机求解。

2)初级铁心和主磁极磁导率为各向同性的特征。

3)磁场仅分布电机内部，初级外部及次级钢轴内部磁位值均为零。

4)铁心的磁导率为无限大，电导率为零，即忽略铁心磁阻。

5)各场量随时间作正弦规律变化。

在上述假设条件下加上相应的边界条件电机内电磁场满足微分方程［4］:

式中:A为向量磁位;μ为磁阻率;γ为电导率;Γ1为第二类边界条件;C1为常数。

通过直线感应电动机的轴对称性与边界条件，用二维法求解出圆筒形直线感应电动机的模型图，如图1所示。

图1 圆筒形直线感应电动机的求解模型

2 电机性能的有限元计算

图2是圆筒形直线感应电动机的等效电路。图中，初级绕组的电阻和漏抗为Rs和Xs;励磁电阻是Rm，电抗是Xm;次级铁心表面的电阻为，电抗是;由于端部效应的影响，纵向边的电功率损耗值按照一定的算法折算成等效电阻是Red;在次级铜层中的折算的电阻值是;电源电压是U1。

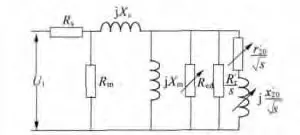
图2 圆筒形直线感应电动机等效电路

设圆筒形直线电动机每极每相槽内的向量磁位为A，则可以通过下式计算出初级每相绕组的总磁通:

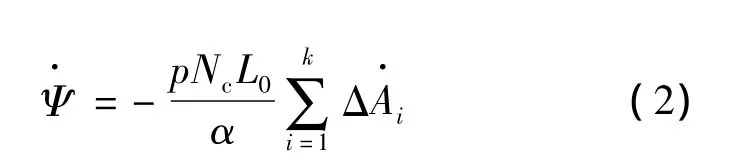
式中:α为并联支路对数;p为极对数;Nc为线圈的匝数;L0为铁心有效长度;i=1～k为每极每相槽数;ΔA·i是第i个线圈在横截面中心的两条边之间的向量磁位差，通过电磁感应定律，每一相绕组中的感应电势:

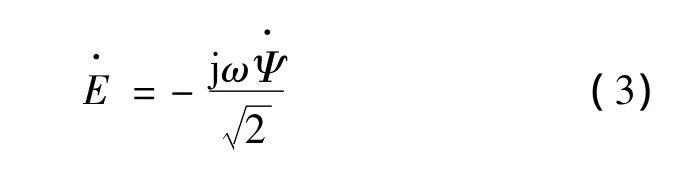
由图2的等效电路，圆筒形直线感应电动机的每相端电压:

3 有限元计算结果

利用有限元分析软件ANSYS 12.0通过对直线电机的详细分析，根据对称性与其相应的边界条件，由圆柱坐标系可以通过其尺寸大小建立电机的模型，模型如图1所示。

建立好实体模型后需要对模型进行网格划分，网格划分是ANSYS有限元分析中最关键的一步，尤其是直线电动机中气隙的处理最为重要。因为在电机中，定子和动子不存在机械接触，机电能量的转换主要是通过气隙来传递的，所以网格划分的时候一定要细，这样才能保证电磁场计算的准确性。网格划分结果如图3所示。

图3 圆筒形直线感应电动机网格划分结果

3.1 磁力线分布图

选择求解器，对模型进行求解，得出磁力线的分布图，如图4所示。从图中可以看出，电机共有16个极，包括15个完整的磁极和一个两端被切断的磁极。磁力线经过电机磁轭，电机齿部进入气隙，并穿入次级，再通过气隙进入另外一个电机齿部耦合，最终形成一个极的主磁路的闭合路径。

图4 圆筒形直线感应电动机磁力线分布图

3.2 磁感应强度矢量图

图5 是圆筒形直线感应电动机的磁感应强度矢量图。从图中可以看到，直线电机中磁感应强度矢量的大小和方向，其中颜色强度的变化代表模型中由于位置的不同而造成的磁感应强度大小的值。本文所研究的圆筒形直线感应电动机的磁感应强度最大值为0.59 T。

图5 圆筒形直线感应电动机磁场强度矢量图

3.3 磁密分布

图6 是磁感应强度在直线感应电动机上的分布。由图中可以看出，边端效应对该电机的影响很小，可以忽略，但磁密比较高。主要是因为该电机的结构材料影响的原因。图7是沿电机气隙路径上的磁感应强度曲线，从图上可以看到电机有16个极。

图6 磁感应强度分布图

图7 沿气隙路径上的磁感应强度曲线

3.4 推力分析

各相绕组的阻抗值由于电机两端的开断使得其不对称，从而导致电机内部的气隙发生畸变，进而使得起动推力大大减小。其起动电磁推力:

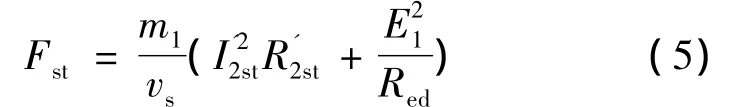
式中:m1为相数为 次级归算电流为 次级绕组所归算的电阻值;E1为感应电动势;Red是由于端部效应的影响，纵向边端的电功率损耗值按照一定的算法折算成的等效电阻。通过有限元分析，得出起动推力为274.9 N，而实验值为270.7 N，误差为1.53%。表明采用有限元的方法得到的结果和实验值非常吻合，证明了这种方法的正确性。

另电机其它尺寸不变，改变气隙大小，分别计算各气隙大小的圆筒形直线感应电动机的涡流场。分别计算气隙为 0.5 mm、1.0 mm、1.5 mm、2.0 mm、2.5 mm、3.0 mm时电机的起动推力，得到推力随气隙的变化曲线，如图8所示。随着气隙的增加，电机起动推力直线下降，气隙小于2 mm时，推力减小速度较慢;大于2 mm时，减小速度变快，表明起动推力与气隙不成线性变化关系。保持电机初级尺寸不变，次级铜层厚度分别取 0.5 mm、1.0 mm、1.5 mm、2.0 mm、2.5 mm、3.0 mm 时，计算得到电机推力随次级铜层厚度的变化曲线，如图9所示。从图中可以看出，当厚度从0.5 mm增大到1.5 mm，推力从186 N迅速增大到280 N;当厚度从1.5 mm增大到3.0 mm时，推力逐渐减小，表明圆筒形直线感应电动机次级铜层厚度与电机推力成非线性关系。

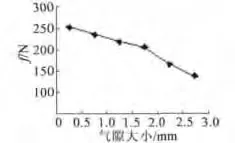
图8 推力随气隙变化曲线

图9 推力随次级铜层厚度变化曲线

表2 不同铜层厚度下起动推力的计算值和实验值

4 结 语

本文采用有限元的方法，对圆筒形直线感应电动机进行了分析，进而计算出其运行特性，得到如下结论:

1)采用有限元法，通过对圆筒形直线感应电动机的起动性能进行仿真，结果与实验值非常吻合。

2)受到端部效应的影响，圆筒形直线感应电动机初级两端出现漏磁现象，并且磁场分布不规则，两端齿部磁密较小。

3)随着气隙的增加，圆筒形直线感应电动机纵向边端效应增加，其漏磁现象就越明显，推力减小，并且不成线性变化。

4)随着次级铜层厚度的增加，感应电流通过路径的电阻减小，推力增大，但是随着厚度的继续增加，次级导磁路径和初级的距离增大，推力减小。

［1］叶云岳.直线电机原理与应用［M］.北京:机械工业出版社，2000.

［2］上海工业大学，上海电机厂.直线异步电动机［M］.北京:机械工业出版社，1979.

［3］叶云岳.国内外直线电机技术的发展与应用综述［J］.电器工业，2003(01):18－22.

［4］张晓晨，李伟力，曹君慈，等.屏蔽电机屏蔽损耗与电机性能的计算与分析［J］.哈尔滨工业大学学报.2007，39(9):83－87.