单矢量水听器频域极化加权MUSIC算法
刘 伟,朴胜春,祝捍皓
(1.哈尔滨工程大学水声技术重点实验室,黑龙江哈尔滨150001;2.哈尔滨工程大学水声工程学院,黑龙江哈尔滨150001)
单矢量水听器频域极化加权MUSIC算法
刘 伟1,2,朴胜春1,2,祝捍皓1,2
(1.哈尔滨工程大学水声技术重点实验室,黑龙江哈尔滨150001;2.哈尔滨工程大学水声工程学院,黑龙江哈尔滨150001)
针对经典多重信号分类(MUSIC)算法估计性能受限于空间随机分布噪声的问题,提出了一种基于频域极化加权的单矢量水听器MUSIC算法。该方法提取接收信号频域极化参数,根据目标信号与噪声在极化特性上的区别,对接收信号频谱自适应地加权。将加权后的频谱信号代替原接收信号,构造极化协方差矩阵,再利用经典MUSIC算法估计目标方位。仿真研究表明,在信噪比为-15 dB且无先验知识情况下,该方法的目标方位估计误差小于5°。海试数据处理结果验证了该方法的有效性。
单矢量水听器;高分辨方位估计;频率域极化分析;多重信号分类
矢量水听器可以共点同步地测量声场的声压和振速信息,且仅用单个矢量水听器便可实现目标方位估计,因此近年来受到了国内外学者广泛关注。Dovid Levin等研究了最大似然估计方法,通过寻找导向响应功率最大值获得目标方位[1]。Kainam Thomas Wong等讨论了接收矢量水听器远离和靠近边界情况下波束指向性[2-3]。杨士莪利用宽带声压与振速偶次阶矩所组成的联立方程组,获得目标强度和方位[4]。Wong K T等将多重信号分类(multiple signal classification,MUSIC)算法引入矢量信号处理中,对信源个数估计算法和矢量阵MUSIC算法进行了深入研究,联合利用声压和振速信息获得目标方位[5-7]。考虑到单矢量水听器本身阵列流型特点,梁国龙等研究了基于单矢量水听器的MUSIC算法,并探讨了声压振速相位不一致情况下方位估计性能及改进方法[8-9]。袁志勇等提出了一种基于高阶累积量的单矢量水听器MUSIC算法[10]。
单矢量水听器MUSIC算法具有较高的方位分辨力和估计精度,但此方法对信噪比有一定要求,当信噪比下降时,方位估计性能下降。高阶累积量方法虽然具有一定的抗噪声能力,但计算量较大。本文提出一种基于频域极化加权(FDPW-MUSIC)的方位估计方法,首先利用FFT变换获得接收信号的频谱成分,对频域信号进行偏振分析,估计每个频点的极化参数;根据目标信号与噪声在频域极化特性上的差别,对频谱成分自适应加权,减小噪声影响;将加权后频域信号替代接收信号,构造频域协方差矩阵,按照经典MUSIC算法估计目标方位。
1 单矢量水听器数学模型
1.1 接收信号时域模型
理想情况下,M个远场不相干信号入射到矢量水听器上,单个矢量水听器接收信号模型为

式中:p(t)为声压信号,v(t)为振速信号,A=[a1,a2,…,aM]是单矢量水听器4×M维阵列流型,s(t)是M×1维的空间信号模型,θm为第m个入射信号在xoy平面投影与x方向的夹角,称为方位角;φm为第m个入射信号与信号在xoy平面投影之间夹角,称为俯仰角;n(t)为矢量水听器测得的4×1维高斯白噪声,声压和振速方差均为σ2,且与信号不相关。
1.2 矢量信号频域协方差矩阵
假设信号广义平稳,对y(t)进行傅里叶变换,将信号从时域变换到频域

矢量水听器接收信号的频域协方差矩阵为
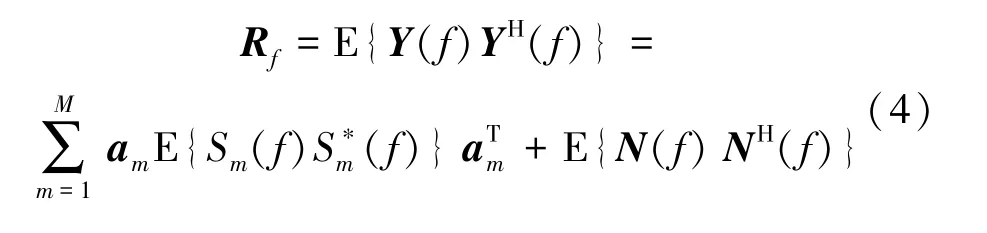
根据式(1)可得接收信号的时域协方差矩阵:

信号单位时间内的能量与单位频率内的能量满足帕斯瓦尔定理[11]
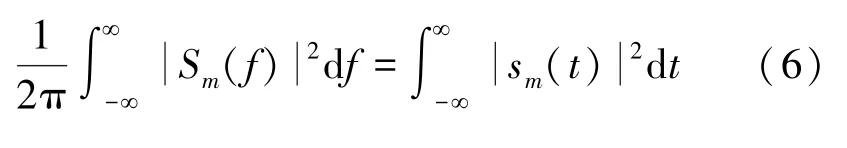
将式(6)代入式(4)、(5)中,得到频域协方差矩阵与时域协方差矩阵的关系:

由上式可知,Rf与2πRt是相等矩阵。若对Rf和Rt进行特征分解,其对应的特征矩阵也是相等的,特征值相差2π倍,即采用Rf估计信号源个数或目标方位,可以获得与Rt完全相同的处理结果,并不会影响算法估计性能。因此,可利用频域协方差矩阵代替时域协方差矩阵实现高分辨方位估计。
2 FDPW-MUSIC算法
2.1 频域极化参数提取
偏振的概念最早起源于光学,现已广泛应用于地震学和电磁学等领域[12-14]。 极化又称偏振,是矢量信号的共有属性,用于描述质点运动轨迹。水中传播的声波为纵波,当入射信号中仅存在直达声时,接收信号的空间质点运动轨迹是直线,其传播方向和质点位移方向保持一致,偏振特性为线性;近距离时,由于多途结构的存在,声源发出的信号通过不同途径到达接收点,接收声波为多个相同频率的平面波叠加,合成的振速矢量是旋转矢量;远距离时,相干多途信道对信号的影响逐渐减小,基本可忽略,此时信号的传播方向和质点位移方向基本一致,偏振轨迹近似为直线。因此,在流体和气体声场中,偏振的概念也成立,并可以用偏振分析将椭圆的属性表示为定量值[15]。
振速v(t)的3个分量为vx(t)、vy(t)和vz(t),分别对其进行FFT变换,获得频域信号Vx(f)、Vy(f)、Vz(f)。在进行FFT变换时,需要适当的选择截取信号的长度,避免因为信号过短导致频率分辨率过低,造成2个不相干目标的频谱产生混叠。在某一频率f以一定带宽δ求得谱密度矩阵:

式中:i,j=x,y,z。时域协方差矩阵的特征值和特征向量可以定量分析信号极化程度和极化方向。若信号的质点运动轨迹是直线,协方差矩阵只有1个非零特征值,其相应的特征向量代表了信号的极化方向;如果信号的质点运动轨迹是椭圆,则有2个非零特征值,其相应的特征向量确定这个椭圆平面。仿照时域处理方法获得频域极化参数,对谱密度矩阵进行特征分解,由于谱密度矩阵为Hermitian矩阵,特征分解能够获得3个非负特征值,记为λ1、λ2和λ3(λ1>λ2≥λ3)。通过特征值定义频域信号的极化度:

若不进行特征分解,极化度还可以利用:

式中:l代表信号维数,Tr代表矩阵的迹。极化度反应的是信号的偏振程度,在0~1内变化。若η=0,表明极化状态是随机的,若η=1,状态为完全极化。
2.2 频域极化加权
由于接收信号由M个不相干信号共同构成,信号的频谱互不重叠。若第m个信号对应频率为fm,当δ足够小时,可以认为频带fm-δ~fm+δ内仅包含第m个信号,由式(3)、(9)可知,此频带范围内的谱密度矩阵为

文献[13-14]中直接利用极化度的Q次幂作为加权函数即

当信噪比较高时,噪声的极化度接近0,上式具有一定的抗噪声能力。但当噪声功率增加或某一频段内噪声的功率不是完全随机的,信号的极化度减小,而噪声的极化度增加,采用上式进行加权,反而会导致信号能量减小。将频域极化加权函数表示为高斯函数形式,可在信噪比较低时获得更好的加权效果,即

式中:η0为期望极化度,ση为直线性标准差。当噪声未将信号淹没时,信号的极化度值大于噪声极化度,因此可将最大极化度值作为期望极化度;为了更好地抑制噪声,直线性标准差不能设定过大,通常为0.1~0.2.
在式(13)中,加权函数是高斯函数,当信号直线性接近η0时,权值较大,接近于1;反之,当直线性小于η0时,权值急剧下降。利用式(12)对频域信号加权,获得修正的频域信号:

式(13)中参量η(f)反映了不同频率的极化特性。式(13)、(14)利用此特性设计频域滤波器,可自适应地对接收信号进行加权,在频率域上去除与目标信号极化特性不同的干扰成分,且无损失的保留目标信号成分。
不同于常规窄带滤波器,在使用时需要已知目标信号信息,本文方法能够在无目标信号先验知识情况下,自适应地提高其信噪比。
采用频域极化加权后信号进行高分辨方位估计时,噪声对算法性能的影响将显著降低,高分辨方法的处理效果将明显提高。
2.3 MUSIC算法
由加权后的频域信号Z(f)替代接收信号,按照式(4)获得频域协方差矩阵,对Rf进行特征分解:
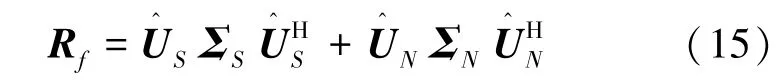
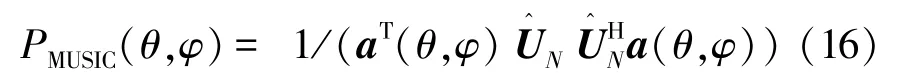
在利用阵列估计目标方位时,远场信号到达阵列阵元的时延值与信号的频率直接相关,若目标信号为宽带信号,在估计方位前必须对接收信号进行聚焦;而单矢量水听器可以共点同步采集声压和振速信号,远程信号同时到达接收的4个阵元,对于宽带信号不需聚焦处理,可直接采用上述方法估计信号来波方向。
3 FDPW-MUSIC算法统计特性分析
仿真环境:仿真的远场目标信号为100 Hz的单频信号,样本长度为1 s,采样频率4 000 Hz,方位角为30°,俯仰角为45°,噪声为带宽2 000 Hz的零均值高斯噪声,按照式(1)/(2)仿真声压和振速信号。无噪声时仿真信号时域图见图1,仿真的声压信号功率为0 dB,vx通道信号功率为-4.26 dB,vy通道信号功率为-9.03 dB,vz通道功率为-3.01 dB,若无特殊情况,以上参数均保持不变。
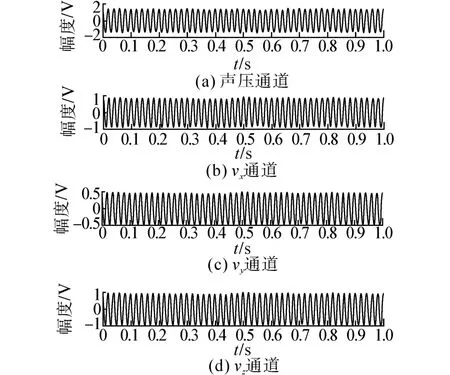
图1 无噪声时仿真信号时域图Fig.1 Time-domain of simulation signals without noise
当声压通道信噪比为-10 dB时,根据文中所述方法计算接收信号的空间谱,图2为频域极化加权MUSIC算法和经典MUSIC算法输出空间谱,搜索步长为0.1°,FFT点数为信号长度。算法的估计性能严重下降,其谱峰不再尖锐,主旁瓣比降低;而文中提出的频域极化加权MUSIC算法主瓣仍然尖锐,主旁瓣比也较高,最大值位置更靠近目标方位理论值。

图2 信噪比为-10 dB时,频域极化加权方法和经典方法Fig.2 MUSIC spectrum of FDPW method and classical method when SNR is-10 dB
图3、4为声压通道信噪比不同变化情况下方位估计性能对比图,搜索步长为1°,计算结果为50次独立实验的统计数据。为了对比改进方法性能,图3、4也给出了在经典MUSIC算法和文献[16]的加权互谱直方图方法估计性能。

图3 不同信噪比下方位角估计标准差和误差均值Fig.3 The deviation and mean error of bearing angle

图4 不同信噪比下俯仰角估计标准差和误差均值Fig.4 The deviation and mean error of pitch angle
由图3、4可以看出:当信噪比高时,3种方法估计误差比较接近,误差均值也在0°附近,估计结果基本是无偏估计;当信噪比下降到0 dB时,加权互谱直方图方法估计性能严重下降,误差很大,而且是有偏估计;当信噪比下降到-5 dB时,经典MUSIC算法估计误差也开始增大;当信噪比下降到-10 dB时,经典MUSIC算法的估计误差均值大于1°,估计不再是无偏的。在信噪比为-5~-10 dB,加权互谱直方图的估计标准差随着信噪比降低而减小,这是因为估计值是有偏的,并且偏离的度数随着信噪比降低而增加,需要综合考虑误差均值和标准差以评估加权互谱直方图方法性能。当信噪比为-15 dB时,经典MUSIC算法方位角估计标准差已经接近60°,俯仰角标准差也接近22°;加权互谱直方图方位角估计标准差达到100°,综合考虑误差均值和标准差,俯仰角误差大概为50°;而文中所提方法的相应标准差远小于其他2种方法。
由此可知,频域极化加权MUSIC算法在信噪比较低且无信号的先验知识情况下,具有较稳定的方位估计性能。
4 海试数据方位估计结果
实测数据为中心频率80 Hz的CW脉冲,脉冲段度为40 s,截取脉冲中较稳定的一段信号进行分析和处理,截取信号时间长度为30 s,采样频率为500 Hz。接收信号为声压和2个水平振速分量分别记为p、vx和vy,实测信号时域图见图5。
由图5可以看出,3个通道信号中均存在很多瞬态干扰,信噪比较低。按照本文方法计算目标方位角,绘制时间-方位历程图,如图6(a),为了验证本文方法的性能,同时给出了经典MUSIC算法、75~85 Hz滤波后经典MUSIC算法和互谱直方图方法获得的时间-方位历程图,见图6(b)~(d),搜索步长均为0.1°,绘制瀑布图时,小窗长度为1 s,FFT点数为信号长度。由于互谱直方图方法对信噪比要求较高,使用该方法之前先对接收信号进行了滤波,滤波通带为78~82 Hz。
对比图6的4个图可以看出,由于噪声的存在,经典MUSIC算法谱峰尖锐,但估计结果不稳定,2个相邻时刻目标方位估计值最大相差30°,估计结果准确性下降;本文所提出方法的谱峰也很尖锐,可以直接获得目标估计值,并且估计结果非常稳定,基本都在-34~-35°内,2个相邻时刻目标方位估计值最大相差不到3°;在对接收信号进行78~82 Hz滤波后,通过加权互谱直方图方法可以观测到目标方大致方位;经75~85 Hz滤波后,经典MUSIC算法估计性能明显提高,方位估计结果与频域极化加权MUSIC算法基本一致,验证了本文所提方法的准确性。通过仿真和实验数据可知,本文所提方法无需信号的先验知识及预处理,即可自适应地获得较稳定的目标方位估计结果。
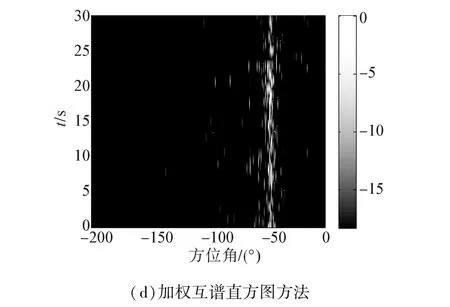
图6 时间-方位历程图Fig.6 Time-bearing display of the received signals
5 结论
通过仿真数据和实测信号分析,得出以下结论:
1)新方法能够利用信号的极化特性,自适应获得极化权值,无需先验知识,更适用于被动检测与追踪;
2)信噪比低时,新方法的空间谱输出仍然非常尖锐,具有很好的目标分辨能力;
3)新方法的统计特性非常稳定,在信噪比低时仍是无偏估计,且估计标准差较小,可用于远程目标分析或微弱信号分析;
4)新方法不仅对高斯白噪声有抑制能力,还可降低瞬态干扰的影响,使其具有较好的工程应用前景。
[1]LEVIN D,HABETS A P,GANNOT S.Maximum likelihood estimation of direction of arrival using an acoustic vector-sensor[J].J Acoust Soc Am,2012,131(2):1240-1248.
[2]WONG K T,CHI H.Beam patterns of an underwater acoustic vector hydrophone located away from any reflecting boundary[J].IEEE Journal of Oceanic Engineering,2002,27(3):628-637.
[3]KESHAVARZ H.Beam patterns of an underwater acoustic vector hydrophone located near a reflecting boundary[C]//Proceedings of OCEAN’04.Kobe,Japan,2004:585-588.
[4]杨士莪.矢量传感器多目标分辨的一种方法[J].哈尔滨工程大学学报,2003,24(6):591-595.
YANG Shi'e.Method of multi-sources distinguishing by single vector transducer[J].Journal of Harbin Engineering University,2003,24(6):591-595.
[5]WONG K T.Self-initiating music based direction finding in underwater acoustic particle velocity-field beam space[J].IEEE Journal Oceanic Engineering,2000,25(2):262-273.
[6]张揽月,杨德森.矢量阵自初始化MUSIC算法的试验研究[J].哈尔滨工程大学学报,2008,29(11):1185-1189.
ZHANG Lanyue,YANG Desen.Experimetnal research on a selfinitiating MUSIC algorithm for direction finding using a vector-hydrophone array[J].IEEE Journal Oceanic Engineering,2008,29(11):1185-1189.
[7]JIANG L,CAI P,WANG Y L,et al.A new source number estimation method based on the beam eigenvalue[J].Journal of Marine Science and Application,2012,6(1):41-46.
[8]梁国龙,张锴,付进,等.单矢量水听器的高分辨方位估计应用研究[J].兵工学报,2011,32(8):986-990.
LIANG Guolong,ZHANG Kai,FU Jin,et al.Research on highresolution direction-of-arrival estimation based on an acoutic vector-hydrophone[J].Acta Armamentarii,2011,32(8):986-990.
[9]梁国龙,张锴,范展,等.单矢量传感器MUSIC算法的DOA估计及性能评价[J].哈尔滨工程大学学报,2012,33(1):30-36.
LIANG Guolong,ZHANG Kai,FAN Zhan,et al.Performance evaluation of DOA estimation using a single acoustic vector-sensor based on an improved MUSIC algorithm[J].Journal of Harbin Engineering University,2012,33(1):30-36.
[10]袁志勇,顾晓东.单矢量水听器四阶累积量MUSIC算法对信号DOA的估计[J].舰船科学技术,2010,32(6):64-67.
YUAN Zhiyong,GU Xiaodong.MUSIC algorithm based on highorder cumulant for DOA estimation using a single vector hydrophone[J].Ship Science and Technology,2010,32(6):64-67.
[11]奥本海姆.信号与系统[M].2版.刘树棠,译.西安:西安交通大学出版社,2003:220-222.OPPENHEIM A V.Signals&systems[M].2nd ed.LIU Shutang.Xi'an:Xi'an Jiao Tong University Press,2003:220-222.
[12]王克让,朱晓华,何劲.基于矢量传感器MIMO雷达的DOD,DOA和极化联合估计算法[J].电子与信息学报,2012,34(1):160-165.WANG Kerang,ZHU Xiaohua,HE Jin.Joint DOD DOA and polarization estimation for mimo radar with electromagnetic vector sensors[J].Journal of Electronics& Information Technology,2012,34(1):160-165.
[13]陈赟,高乐,赵烽帆.提一种基于频率域偏振分析提高三分量地震资料信噪比的方法[J].地球物理学进展,2007,22(1):255-263.
CHEN Yun,GAO Le,ZHAO Fengfan.A method to enhance the signal/noise ratio of three-component seismic data based on the polarization analysis in frequency domain[J].Progress in Geophysica,2007,22(1):255-263.
[14]SAMSON J C,OLSON J V.Data-adaptive polarization filters for muhichannel geophysical data[J].Geophys,1981,46(10):1423-1431.
[15]B.A.休罗夫.海洋矢量声学[M].贾志富,译.北京:国防工业出版社,2011.
SHCHUROV B A.Vector acoustics of the ocean[M].JIA Zhifu.Beijing:National Defense Industry Press,2011.
[16]姚直象,惠俊英,殷敬伟,等.基于单矢量水听器四种方位估计方法[J].海洋工程,2006,24(1):122-131.
YAO Zhixiang,HUI Junying,YIN Jingwei,et al.Four approaches to DOA estimation based on a single vector hydrophone[J].The Ocean Engineering,2006,24(1):122-131.
The frequency domain polarization weighted MUSIC algorithm using a single vector hydrophone
LIU Wei1,2,PIAO Shengchun1,2,ZHU Hanhao1,2
(1.Acoustic Science and Technology Laboratory,Harbin Engineering University,Harbin 150001,China;2.College of Underwater A-coustic Engineering,Harbin Engineering University,Harbin 150001,China)
This paper analyzes a frequency domain polarization weighted multiple signal classification(MUSIC)algorithm using one vector sensor against the restriction of randomly distributed noise in space.After the frequency domain polarization parameters are picked up,the weights are estimated automatically according to the differences in the polarization characteristics between desired signal and noise.The
signals are replaced by the weighted frequency domain signals to construct the covariance matrix which is used to realize DOA estimation through the MUSIC algorithm.The simulation results show that the estimation error of this proposed method is less than 5°when the signal to noise ratio is-15 dB and there is no prior information.The validity of this improved method has been verified by the sea experiment results.
single vector sensor;high-resolution DOA estimation;frequency domain polarization analysis;MUSIC
�测信号时域图 Fig.5 Time-domain of received signals
10.3969/j.issn.1006-7043.201212115
TN911.7
A
1006-7043(2014)03-0289-06
http://www.cnki.net/kcms/detail/23.1390.U.20131217.0915.001.html
2012-12-31. 网络出版时间:2013-12-17 9:15:50.
国家自然科学基金资助项目(11234002,61240007).
刘伟(1988-),女,博士研究生;朴胜春(1968-),男,教授,博士生导师.
朴胜春,E-mail:piaoshengchun@hrbeu.edu.cn.

