离散时间H∞性能下界研究方法

王宏霞，张焕水，俞 立，陈 欣

离散时间H∞性能下界研究方法

王宏霞1，张焕水2，俞 立1，陈 欣1

（1.浙江工业大学信息工程学院，310023杭州；2.山东大学控制科学与工程学院，250061济南）

为了缩小二分法求解最优H∞性能的搜索范围，降低搜索代价，采用状态空间分析法，提出了一种获取H∞性能下界的方法.与一般方法不同，根据此方法所得的下界仅跟H2Riccati方程的解有关，而不被卷入该Riccati方程的计算.因此，下界的获取简单.不仅如此，该方法还能揭示最优性能与H∞性能（包括最优控制与H∞控制，最优估计与H∞估计）间的区别和联系、分析多扰动通道对H∞性能的影响以及可预演扰动的有效利用对H∞性能的改善.

H2控制；H∞控制；Riccati方程；线性二次

最优LQ控制（即H2控制）与H∞控制是控制理论的两种最基本的控制方式.它们具有不同的控制目标与性能.从频域来讲，这两种控制性能都是对传递函数范数的刻画.最优控制期望通过控制器的设计使闭环系统传递函数的H2-范数最小（最优）；H∞控制则期望通过控制器的调节使闭环系统传递函数的H∞范数（最小）被限定在给定的范围内［1］.简单来讲，H∞控制器的设计旨在使系统的跟踪误差或者干扰对系统的影响尽可能小.因此，H∞控制理论具有广泛的应用背景，如船舶、鱼雷、轧机控制等［2-4］.1989年，Doyle等人将最优控制与H∞控制的频域理论推广到了时域［5］.这套理论的优势在于:首先，将问题的可解性及控制结果最终归结为Riccati方程的可解性（因为Riccati理论已相当成熟［6］）；不仅如此，该理论还有许多其它优点，如可以研究相应的时变问题、有限时域问题等，因而大大拓展了控制理论的研究范围.时域最优H2、H∞的控制目的等价于分别最小化被调节信号的l2范数、最小化一个l2诱导范数，次优H∞控制则期望找到一个控制器使得某l2诱导范数被限制在给定的范围内.与频域法一样，在最优H∞控制性能的量化问题上，由于控制器设计与控制性能相互耦合，时域法至今没能像H2控制一样显式地定量刻画出最优H∞控制性能.尽管如此，将已有的许多H∞控制方法如对策论［7-9］、不变嵌入［10］、不变空间的投影［11］等方法［12］与二分法相结合则可以简单有效地解决最优H∞控制问题.通常情况下，最优H∞性能的搜索区间为（0，γu］，其中，γu是一个足以保证相应次优H∞控制问题可解的正实数.

由于需要求解H∞型Riccati方程，单纯解决次优H∞控制问题的代价已不小，二分法又意味着次优H∞控制问题的多次求解.因此，有必要尽量缩小搜索范围.尝试提出一种刻画H∞性能下界的时域方法，定量刻画H∞性能的下界.该下界获取简单与H∞Riccati方程及惯性条件无关.它不仅能帮助我们快速锚定有效的搜索范围，还有助于揭示最优控制与H∞控制之间的区别、研究多通道扰动对H∞控制性能的影响以及可预演扰动对H∞控制性能的影响.此外，还提出了一个次优H∞控制理论的等价理论.

对于任意的矩阵M、N，M′为矩阵M的转置，ρ（M）为M的谱半径，diag｛M，N｝为主对角线元素是M，N的块对角阵．I为维数相容的单位阵．l2为由所有平方可加的序列x=｛x1，x2，…｝所组成的空间．对于任意的x∈l2，‖x‖2为x的l2-范数．对于任意的向量x∈Rn，｜x｜2为x的2-范数．对于希尔伯特空间中的任意元素x，y，〈x，y〉表示x，y的内积．对于任意的列向量x，y，col｛x，y｝表示由x，y堆叠成的维数为x，y维数之和的列向量．此外，还假设本文中所有变量、矩阵都是维数相容的．

1 问题描述

考虑确定性系统

式中:x为系统状态，u为控制输入，w为扰动输入，z为待调节输出，A，B1，B2，C，D是已知的矩阵．

为了保证所研究的问题有意义，下面是标准假设.

假设1 （A，B2）是可镇定的；

假设2 系统［A，B2，C，D］在单位圆上无不变零点且左可逆；

注意假设2保证了D′D的可逆性．

不失一般性，为了简化问题的后续推导过程会涉及到的符号，还将假设.

假设3 D′［CD］=［0I］．

标准的全息最优H∞控制问题可叙述为:寻找全息控制器使得闭环映射Twz:w｜→z的l2诱导范数最小，即

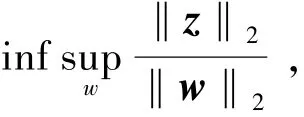
为方便下文的叙述记

如前所述，最优性能与控制器的耦合导致人们很难直接求解最优H∞控制问题.而利用二分法求解最优H∞控制问题的本质在于解决次优H∞控制问题.因此，有必要给出次优H∞控制问题的描述.

全息次优H∞控制问题可叙述如下:对于给定的γ＞0，（判断是否存在，若存在）寻找全息控制器uk使得在它的调节下，对于任意的非零能量有界扰动，闭环映射Twz:w｜→z的l2诱导范数均小于γ，即

由于次优H∞控制问题的可解性等价于两个条件:其一，相应的H∞Riccati方程存在半正定的可镇定解；其二，某惯性条件成立.相对精确的二分法搜索范围则意味着以相对小的代价来解决最优H∞控制.因此，本文的目的在于找到γ0的下界，缩小搜索范围，降低求解最优H∞控制问题的代价.

2 最优H∞控制问题的下界

作为陈述主要结论的准备，首先定义一些符号.引入下面的H2Riccati方程

其中Υ=D′D+B′2XB2．

由于假设1、2的成立，H2Riccati方程存在半正定的可镇定的解且Υ＞0．根据Riccati方程的解X与Υ，定义下面的符号:

其次，引入下面的引理，它本质上是不定空间的投影定理，是给出本文主要结论的关键依据.

引理1［13］已知U与V是希尔伯特空间，S: U｜→V与J∶V｜→V是有界线性算子．若对某个ε＞0，S′JS＞εI，则对于任意的v∈V，最优化问题

存在唯一解且最优解

等价刻画为

上式意味着对于∀u∈U，总有〈Su，J（Su∗-v）〉=0成立．

由于所涉及到的变量都属于希尔伯特空间，所以〈Su，J（Su∗-v）〉=0意味着最优轨道Su∗-v与形如Su的这类轨道正交．

为了分解H∞下界理论的复杂推导，给出次优H∞控制理论的一个等价结论.

定理1 对于给定的γ＞0和系统（1）-（2），γ＞γo的充分必要条件是Λ＜0、Riccati方程

存在半正定、可镇定解，且使Φ+Ψ′ZΨ与diag｛-I，I｝有相同的惯性指数．

证明 必要性的证明基于引理1与下面的差分对策问题［9，13］上式的内层优化是一个LQ优化.根据引理1，假设1、2能够保证muin‖z‖存在唯一的解．具体来讲，记K是系统（1）的一个可镇定状态增益，则u=Kx+u˜，u∈l2参数化了所有的容许控制．对于系统［A-B2K，B2，C-DK，D］，不难证明，与假设1、2类似，（A-B2K，B2）可镇，［A-B2K，B2，CDK，D］在单位圆上无不变零点且左可逆．此时，根据引理1，作如下定义，分别取u˜，l2为引理1中的u，U，算子S:u˜｜→z∶l2｜→l2，是零初始状态时系统［A-B2K，B2，C-DK，D］的输入输出映射．记z˜是初始状态和外部扰动分别为x0和w时系统［A-B2K，B1，C-DK，0］的输出响应，分别取-z˜，l2为引理1中的v，V，J=I，则S′S＞0，（根据假设3，S′S≥I）．此时根据引理1，内层优化存在唯一的最优解u˜#（这同时意味着存在唯一的最优解u#=Kx+u˜#），且最优解可被刻画为S′（Su˜#+z˜）=S′z#=0，这里，z#=Su˜#+z˜是给定初始状态x0，最优控制u#及扰动w时，系统（1）-（2）的输出响应．为方便将来叙述，记x#（x0，w），u#（x0，w），z#（x0，w）均为Rn×l2到l2的有界线性算子，这些算子由最优控制问题的解所决定．

S′z#=0可等价描述为非因果系统的输出响应

u#的最优性意味着由式（1）、（2）、（5）、（6）决定的l2轨道x，z，p，u的最优性．u#的唯一性则意味着初值x0和扰动w给定时式（1）、（2）、（5）、（6）所决定的l2轨道x，z，p，u的唯一性．

现在考虑基于内层优化的外层优化．实际上，γ＞γo意味着:对于任意的δ＞0，总存在容许的全息控制器，使得在它的调节下，对于零初始状态和任意的扰动w∈l2，闭环系统的输出响应总能满足下面的关系

取闭环输出z=z#（0，w），则

分别取w，l2，l2×l2为引理1中的u，U，V，显然（w，z#（x0，w））∈V，再取（0，z#（x0，0））为引理1中的-v，Sw=（w，z#（0，w）），J=diag｛γ2I，-I｝．根据这些定义，式（8）可表示成

再根据引理1，内层优化完成后的外层优化存在唯一最优解w∗，最优w∗满足S′J（w∗，z∗）=0，即

由于S′很难直接计算，令u=Kx是一个可镇定的反馈控制，˜z是在该反馈下、系统（1）-（2）对于零初始状态和给定扰动w的输出响应．记Δz=z#（0，w）-˜z，则式（10）等价于

式（11）中的第2个等式成立是因为z#（x0，w）是初始状态为x0、外部扰动为w时，内层优化的最优轨道，它正交于系统［A，B2，C，D］在零初始状态和任意容许控制驱动下的输出响应．令γ2〈w，w∗〉-（w，˜z）．根据式（11），可以给出最优w∗的另一种等价刻画˜S′J（w∗，z∗）=0．它进一步意味着反因果系统（5）与下式的成立．

总之，式（1）、（2）、（5）、（6）、（12）是最优轨道x，p，u，w的唯一刻画．记u∗（x0）=u#（x0，w∗（x0）），x∗（x0）=x#（x0，w∗（x0）），z∗（x0）= z#（x0，w∗（x0））．

根据式（1）、（2）、（5）、（6）、（12），

对式（13）的两边关于k从0到∞求和，则

为了分离最优w与最优u对最优对策值的贡献，引入下面的线性变化，

分离变换式（15）中的w尚未优化.把式（15）带入式（1）、（5）、（6），可得

观察式（16）发现，ζk完全由ws，s≥k+1所决定，特别地ζ-1包含且仅包含所有的wk，k≥0．注意，式（15）～（17）对任意的w均成立．

现在取w=w∗且将式（15）带入式（14），则有

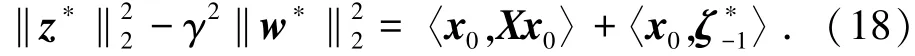
发现，当x0=0时，最优扰动对最优对策值的贡献为0，而wk=0，k≥0对最优对策值的贡献也为0．结合最优解w∗的唯一性，可知x0=0时，最优=0，k≥0，进一步有，=0，=0，k≥0．

如果将对策问题限制在区间［k，∞）上，前面所有关于必要性的分析都成立，当然，间的线性关系依然成立．

相似地，可以结合式（1）、（6）、（12）推导l2最优轨道、最优控制及最优扰动与x0之间的线性关系．根据式（12）、（15）、（17）（为简化符号，以下推导去掉了最优轨道的标志符号∗），

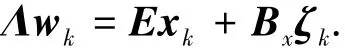
由于最优轨道的唯一性，Λ必然可逆.因此，

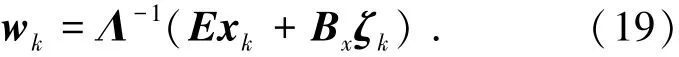
将式（19）带入式（16）、（17），得到

令

其中:s=0，1，…，并将之带入式（20）、（31），则可推得式（3）．I-ΨΦ-1Ψ′的可逆性仍然缘于最优轨道的唯一性．根据最优对策值的表达式（18）、（22），可得最优对策值必然大于等于w=0时的对策值

换句话说，

因此，

从x0的任意性，Z≥0显然成立.式（3）的可镇定性源于最优轨道属于l2空间.

证明Λ的负定性.考虑初始状态为零时的对策问题式（4），根据式（8），γ＞γo意味着其唯一最优解是u∗=0，w∗=0．因此，零初始状态时，w取0外的任意值，只能导致一个严格小于0的对策值．取w0≠0，wk=0，k≥1，u=u#（0，w），参考式（13）、（15）、（21）可得

式（23）立即可导出Λ＜0．

证明惯性条件.众所周知，由式（1）、（5）、（6）、（12）定义的齐次HJB方程有唯一l2解意味着状态与伴随状态之间存在线性关系，则

P=A′PA+C′C-A′PBΠ-1B′PA．（24）

该线性关系完全被Riccati方程的半正定、稳定、及满足Π与diag｛-I，I｝有相同的惯性指数的解所刻画，其中B=［B1，B2］，Π=B′PB+ diag｛-I，I｝．根据式（14），最优对策值可通过P表示为〈x0，Px0〉，这意味着P=X+Z．复杂但直接的代数运算表明，

由此，惯性条件显然成立.

充分性的证明是一个构造式的证明记.

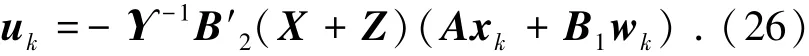
该证明实际上是在式（3）具有给定性质解的前提下，说明式（26）是一个次优H∞全息可镇定反馈控制.

假设Z是式（3）的解，满足定理1中给定的条件．定义P=X+Z，但此时并不知道P=X+Z满足什么样的关系式，具有怎样的性质．因此，接下来需要证明P是某个Riccati方程满足某些性质、条件的解．由于X，Z均是半正定矩阵，所以P也是半正定矩阵．给定初始状态x0，定义ζ-1= Zx0．根据式（3）与HJB式（20）、（21），可推得xk+1=（I-ΨΦ-1Ψ′）-1Aγx0，ζk-1=Zxk，k＞0．接着据此定义xk+1，ζk，k＞0，再根据pk=Xxk+1+ζk定义pk，k≥0，考虑Λ与Υ的可逆性，可根据

及式（21）定义uk，wk，k≥0，最终根据式（2）定义zk，k≥0．

上面的构造如此定义的x，p，u，w是式（1）、（5）、（6）、（12）的l2解．同时，对于这样构造的z，w，还将有下面的等式成立

此时并未作最优性或者唯一性的任何说明.将基于上面的构造及结论建立P所满足的关系.

根据uk，wk的定义式（27）、（19）及pk=Xxk+1+ ζk，作直接的运算可得

其中Π如式（25）所示.

因此，

说明当控制输入与外部扰动分别取上面所构造的控制输入与外部扰动时，系统（1）实际上等价于xk+1=AFx0，AF=（I-ΨΦ-1Ψ′）-1Aγ．有了上面的准备，下面可推导P实际上满足式（24）．记则对于任意的初始状态x0，

由于x0的任意性，左端的核矩阵P必然等于最后一个等号右端的核．直接的代数推导表明，式（28）右端的核矩阵即式（24）的右端．

需要强调的是，AF的稳定性源自构造的解x属于l2．根据式（25），Π的惯性条件是显然的．至此，整个定理的证明完成．

不同于已有的H∞控制理论的推导，引入了一个可逆线性变换来分解u∗与w∗对对策值的贡献，进而推导出等价的H∞控制理论.

将以定理的方式给出本文的主要结果.

定理2 对于系统（1）-（2），考虑最优H∞控制问题，则有

证明 根据定理1，对于任意的γ＞γo，总成立Λ＜0，即

两边关于γ取下确界，则

则结论式（29）是显然的.

尽管定理2仅提供了最优性能的下界而非下确界，但由于仅依赖于H2Riccati方程的半正定稳定解，所提供的下确界求解简单方便.因此，二分法的搜索区域缩至

当扰动通道增加时，最优H∞性能不减.即当另一扰动通道通过系统参数B3进入系统时，ρ（Q）=ρ（［B1，B3］′X（I-B2Υ-1B′2X）［B1，B3］）≥ρ（B′1XBx），不等号右端实际上即单扰动通道相应的H∞性能下界.

当部分扰动可以提前获取时，因为需保证γ2I-Q-EGE′正定，所以ρ（Q-EGE′）必然为最优H∞性能的下界，其中Q=B′1XBx，G＞0．因此，与标准H∞性能下界ρ（B′1XBx）相比，部分扰动可提前获取时，最优H∞性能可能被改进．

3 数值例子

1.869 6；第二种方法，计算H2Riccati方程的解X=可得Q=3.481 3，再计算H∞性能的下界ρ（Q）=1.865 8，此时可锚定最优H∞性能的搜索区间［1.865 8，5］，此时，由于缩小了搜索区间，搜索了13次就找到了最优H∞性能1.869 6.由于每一次搜索都要计算一个H∞Riccati方程，搜索次数每减少一次都意味着少计算一个H∞Riccati方程.因而，对于高维的系统，使用方法降低的搜索代价尤为明显.

4 结 语

本文基于状态空间提出了一种研究离散H∞控制性能下界的方法.因为辛矩阵与Hanmilton矩阵可以相互转化，所以该方法也适用于连续H∞控制性能下界的研究［6］.此外，该方法不仅提供了H∞控制的等价理论，也能够被用于研究复杂的H∞预演控制问题.

［1］ZHOU Kemin，DOYLE J C.Essentials of robust control［M］.New Jersey:Prentice Hall，1998.

［2］王益群，曹栋理，陈星，等.热连轧卷取机踏步系统鲁棒H∞控制研究［J］.机械工程学报，2002，38（10）: 62-64.

［3］段富海，彦卫国，何长安.一种非线性优化控制方法及其在鱼雷控制中的应用［J］.控制理论与应用，2000，7（1）:65-68.

［4］张显库.船舶运动简捷鲁棒控制［M］.北京:科学出版社，2012.

［5］DOYLE J C，GLOVER K，KHARGONEKAR P，et al．State-space solutions to standard H2and H∞control problems［J］.IEEE Transactions on Automatic Control，1989，34（8）:831-847.

［6］BITTANTI S，LAUB A，WILLEMS J C.The riccati equation［M］.New York:Springer-Verlag，1991.

［7］TADMOR G.Worst-case design in the time domain:the maximum principle and the standard H∞problem［J］. Mathematics of Control，Signals，and Systems，1990，3（4）:301-324.

［8］YAESH I，SHAKED U.Minimum H∞-norm regulation of linear discrete-time systems and its relation to linear quadratic discrete games［J］.IEEE Transactions on Automatic Control，1990，35（9）:1061-1064.

［9］BASAR T，BERNHARD P.H∞-optimal control and related minimax design problems:a dynamic game approach［M］.Boston:Birkhauser，1995.

［10］BENSOUSSAN A，DA PRATO G，DELFOUR M，et al．Representationandcontrolofinfinitedimensional systems［M］.Boston:Birkhauser，2007.

［11］HASSIBI B，SAYED A，KAILATH T.Indefinitequadratic estimation and control:a unified approach to H2and H∞theories［M］.Philadelphia:Society for Industrial Mathematics，1999.

［12］ZHOU Kemin，DOYLE J，GLOVER C.Robust and optimal control［M］.New Jersey:Prentice Hall，1996.

［13］TADMOR G，MIRKIN L.H∞control and estimation with preview-part I:matrix ARE solutions in continuous time［J］.IEEE Trnsactions on Automatic Control，2005，50（1）:19-28.

（编辑 苗秀芝）

Lower bound for discrete-time H∞performance

WANG Hongxia1，ZHANG Huanshui2，YU Li1，CHEN Xin1
（1.School of Information Engineering，Zhejiang University of Technology，310023 Hangzhou，China；2.School of Control Science and Engineering，Shandong University，250061 Jinan，China）

The paper aims to provide an approach to obtain a lower bound of H∞control performance in state space.It is not involved in algebraic manipulation of Riccati equation and only concerned with the solution to the standard H2Riccati equation.As a consequence，the approach can help one to narrow the optimal H∞performance search via bisection method to a smaller range and considerably reduce the search cost.In addition，the approach enables us to have an insight into not only the link and difference between the optimal performance and the H∞performance including the optimal control and H∞control performance，the optimal estimation and the H∞estimation，but also the impact of the multiple-channel disturbances or previewable disturbance on the H∞control performance.

H2control；H∞control；riccati equation；LQ

TP13

A

0367-6234（2014）06-0123-06

2014-01-09.

国家自然科学基金资助项目（61203045）；浙江省自然科学基金资助项目（LQ14F030004）.

王宏霞（1980—），女，博士，助理研究员；张焕水（1963—），男，教授，博士生导师；俞 立（1961—），男，教授，博士生导师.

王宏霞，whx1123＠126.com.