基于改进的迭代容积卡尔曼滤波姿态估计

钱华明，黄 蔚，孙 龙

基于改进的迭代容积卡尔曼滤波姿态估计

钱华明，黄 蔚，孙 龙

（哈尔滨工程大学自动化学院，150001哈尔滨）

为了充分利用新的量测信息，提高姿态估计的精度，在分析现有迭代滤波策略存在问题的基础上，采用一种新的容积点迭代策略，将其与容积卡尔曼滤波算法相结合，提出了一种改进的迭代容积卡尔曼滤波（improved iterated cubature Kalman filter，IICKF）算法.该算法采用容积数值积分理论近似非线性函数的均值与方差，利用状态扩维理论来解决量测迭代中量测噪声与状态相关的问题，同时利用一种新的容积点迭代策略，即在量测迭代过程中直接采用容积点迭代，避免每步迭代都进行均方根计算来产生容积点，克服传统迭代策略是基于高斯近似产生采样点的局限，有效地降低扩维带来的计算量.仿真结果表明：该算法的估计精度高于乘性扩展卡尔曼滤波（multiplicative extended Kalman filter，MEKF）以及迭代容积卡尔曼滤波（iterated cubature Kalman filter，ICKF）算法，该算法的提出有助于提高姿态估计的精度.

姿态估计；改进的迭代容积卡尔曼滤波；容积数值积分理论；状态扩维；估计精度

针对星敏感器与陀螺仪组成的非线性姿态估计系统，基于非线性滤波的姿态估计方法［1-4］得到了广泛的应用.扩展卡尔曼滤波（extended Kalman filter，EKF）由于其结构简单、易于实现等优点被广泛应用于姿态估计中.但是，EKF存在一定的局限性:1）由模型线性化引入的截断误差会导致滤波精度下降，且需要计算较为复杂的雅克比矩阵；2）当初始状态误差较大或系统模型非线性程度较高时，会严重影响滤波精度甚至导致滤波发散.为了改善EKF估计性能，文献［5］基于Gauss-Newton迭代理论，提出了迭代EKF（iterated extended Kalman filter，IEKF）算法，在量测过程中通过迭代步骤充分利用新的量测信息，降低非线性量测的影响，从而提高估计精度，但是它始终是以EKF为基础，对状态估计精度提高的程度有限.

为了克服EKF算法的局限性，有学者提出无迹卡尔曼滤波算法（unscented Kalman filter，UKF）［6］.UKF通过采用Sigma点近似非线性系统的均值与方差，相比于一阶线性化近似的EKF，该算法避免了求取雅克比矩阵，且估计精度能够达到二阶.然而，UKF算法对于初始误差较大和系统非线性程度高的情况，也存在与EKF类似的缺点.为此，文献［7］采用与IEKF同样的迭代理论，提出了一种迭代Sigma点卡尔曼滤波.文献［8］提出另一种迭代UKF算法，通过使用更新的估计信息来产生新的Sigma点，然后采用与UKF同样的量测更新策略.类似的算法在文献［9-11］中均有报道，但是在这些迭代策略中，每步迭代时状态都引入了量测噪声，破坏了迭代过程状态与噪声不相关的假设，影响了估计精度，同时每次迭代都是通过状态进行迭代，且都是通过高斯近似以及均方根的运算来产生Sigma点.文献［12-13］提出了一种新的非线性滤波，容积卡尔曼滤波（cubature Kalman filter，CKF），其核心思想是针对非线性高斯系统，采用容积数值积分理论近似状态的后验均值和协方差，可以保证在理论上以三阶多项式逼近任何非线性高斯状态的后验均值和方差，相比于UKF，在高维情况下，具有实现简单，滤波精度高，收敛性好等优点.但同样存在与UKF类似的问题.文献［14］将Gauss-Newton迭代理论与CKF相结合，提出了一种迭代的容积卡尔曼滤波算法（iterated cubature Kalman filter，ICKF），但并未改变迭代策略中存在的问题.为此，本文以非线性程度较高的姿态估计系统为背景，提出了一种改进的迭代容积卡尔曼滤波算法（improved iterated cubature Kalman filter，IICKF）.通过分析以往迭代滤波中存在的迭代过程中状态与噪声相关的问题，提出采用状态扩维方法解决该问题，该方法直接对容积点进行迭代更新，避免通过求取高斯近似和均方根的方法来产生容积点，能够充分利用量测信息，从而提高对状态的估计精度.仿真结果表明，IICKF估计精度要高于ICKF.

1 非线性姿态估计模型

1.1 陀螺测量模型

假设陀螺的测量模型为

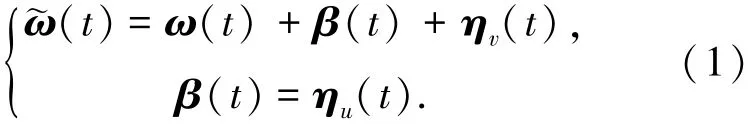
式中:ω˜（t）为陀螺的量测输出值；ω（t）为陀螺的真实角速率；β（t）为陀螺漂移；ηv（t）、ηu（t）为互不相关的零均值白噪声，均方差分别为

1.2 系统状态方程

根据文献［15］的四元数定义规则，姿态运动学方程为

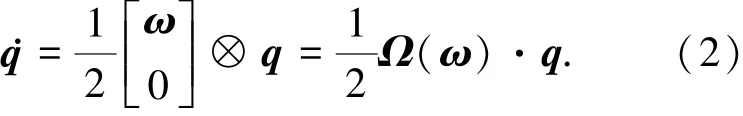
式中:q=[q1q2q3q4]T=[ρTq4]T为姿态四元数；ρ为四元数向量部分；ω为真实角速率；［ω×］为由向量ω的分量构成的反对称矩阵．

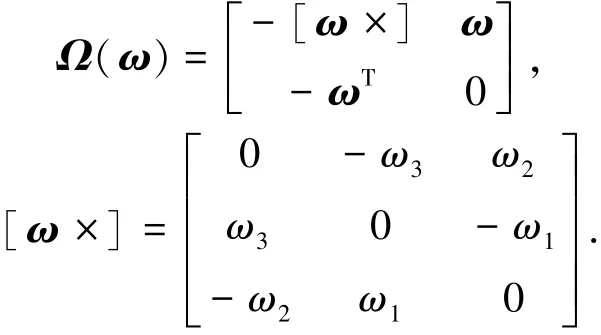
由四元数表示的载体姿态矩阵为

采用乘性误差来定义误差四元数为

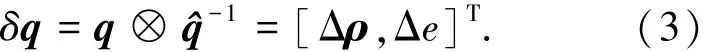
式中:q为真实四元数；＾q为估计四元数；Δρ为误差四元数的矢量部分．

令ω=＾ω+δω，其中＾ω为估计角速率，δω为误差角速率，为陀螺漂移估计值，对式（3）进行求导可得

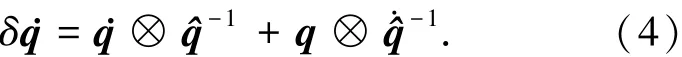
式中:＾q-1为＾q的共轭四元数，由式（2）可知＾q·=＾q，结合四元数的基本性质可得

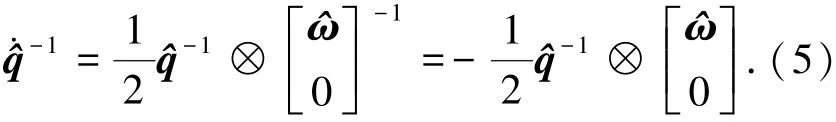
将式（2）、（5）及ω=＾ω+δω代入式（4）可得

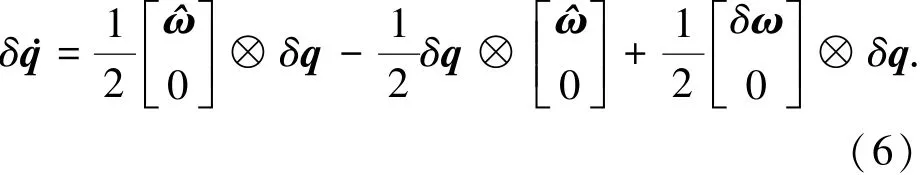
利用四元数乘法，可以求出

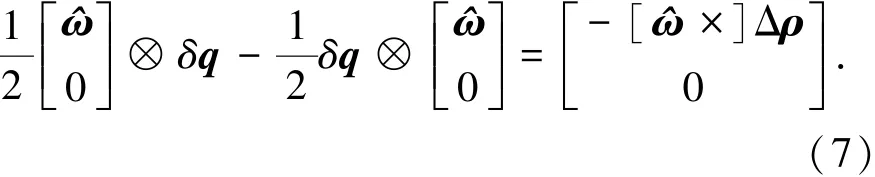
令陀螺漂移估计误差为Δβ，则δω=ω-＾ω= -Δβ-ηv，因此可以求出

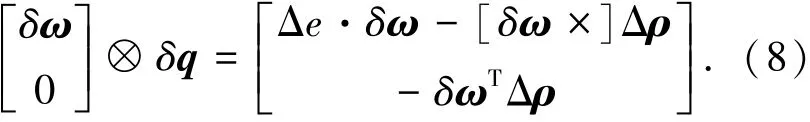
将误差四元数矢量部分Δρ与陀螺漂移估计Δβ组成状态向量，x=［ΔρT，ΔβT］T，建立误差四元数的非线性状态方程为

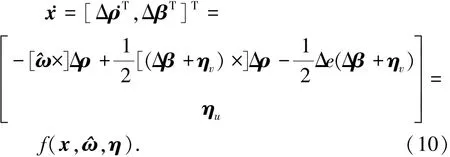
1.3 系统量测方程

星敏感器的测量模型为

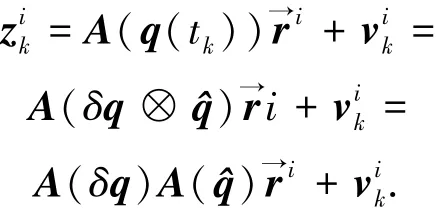
为获得姿态信息，至少需要两个不平行参考矢量的观测值，目前工程应用中常采用3个不平行参考矢量的观测值，则非线性量测模型为

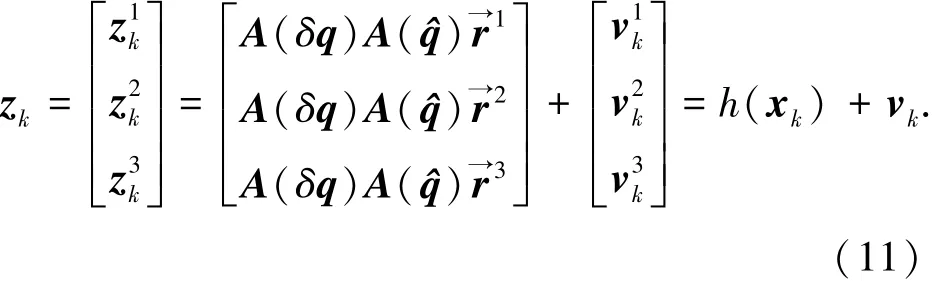
式中:zk为扩维的量测向量；h（xk）为与状态有关的非线性函数；vk为均值等于零，方差为Rk的高斯白噪声．

2 基于IICKF的姿态估计

2.1 ICKF滤波算法

考虑非线性系统为

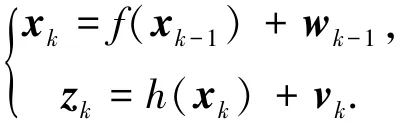
式中:xk、zk分别为系统n维状态向量和p维量测向量；f（·）、h（·）分别为系统非线性状态函数和量测函数；系统噪声wk-1与量测噪声vk分别是均值为零，协方差为Qk-1和Rk的互不相关的高斯白噪声．

采用容积数值积分理论来获取基本的容积点与相应的权值

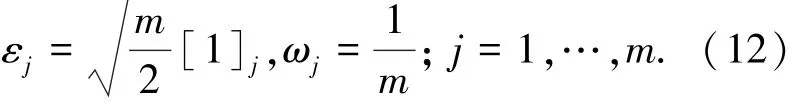
式中:m为容积点总数，且m=2n；εj为第j个容积点；设n维单位向量e=［1，0，…，0］T，使用符号［1］表示对e的元素进行全排列和改变元素符号所产生的点集，称为完整全对称点集，［1］j表示点集中［1］的第j个点；ωj为对应点的权值．

ICKF算法步骤如下.

1）时间更新.容积点及容积点经状态方程的传递值为

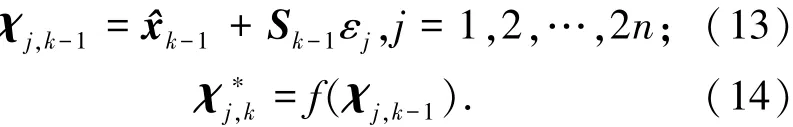
式中:Pk-1=Sk-1（Sk-1）T．

状态预测及方差预测为

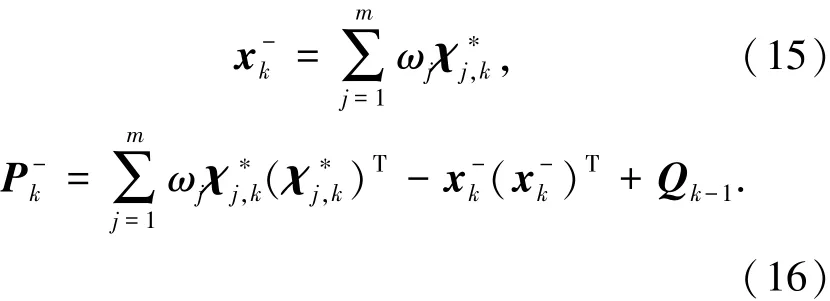
首先计算第i次迭代的容积点及容积点经量测方程的传递值为

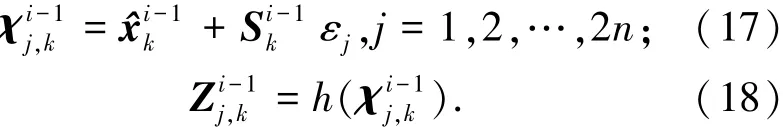
计算量测预测、新息方差及协方差分别为

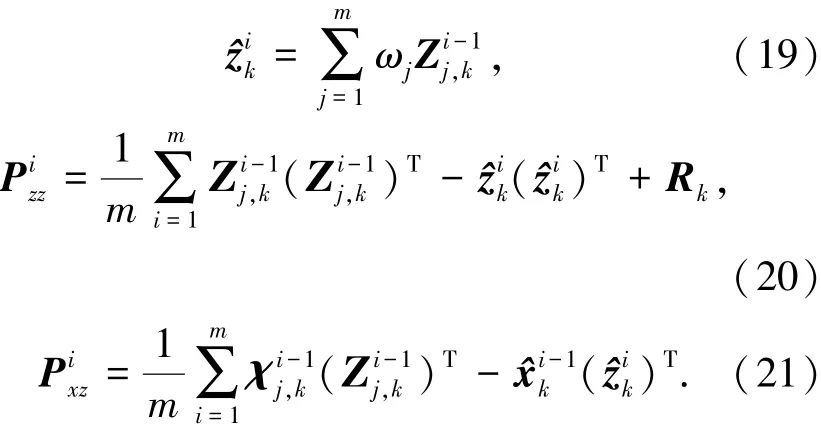
其次计算第i次迭代的滤波增益、状态估计及方差估计分别为

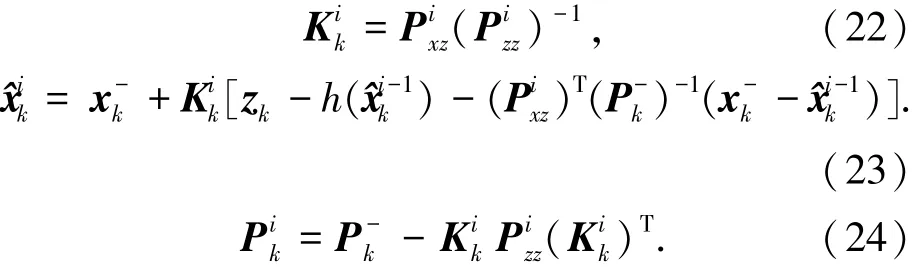
最后迭代终止条件.迭代终止条件为

设迭代终止时的迭代次数为N，则k时刻的状态估计与方差估计为

2.2 IICKF算法的提出

2.2.1 问题分析

从上述迭代容积卡尔曼滤波可以看出，在每一步迭代过程中，量测预测方差和互协方差分别为

在ICKF中，量测噪声在每一步迭代中都是假设与状态及状态估计不相关，因此有

而从状态迭代方程（23）可以看出，在每一次迭代后，状态估计值都加入了量测噪声信息，再将其用于下一步迭代求解量测预测方差及互协方差，就会使得式（28）～（30）不成立，会影响最后的估计精度．因此，为解决这个问题，可以采用状态扩维理论，在量测迭代更新前，将预测状态与量过程如下．

首先计算第i次迭代的容积点及容积点经量测方程的传递值为

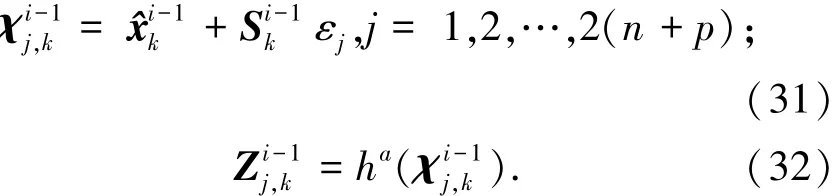
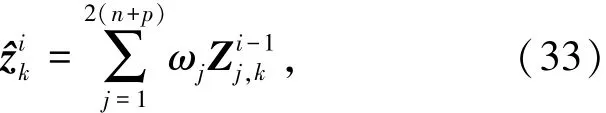
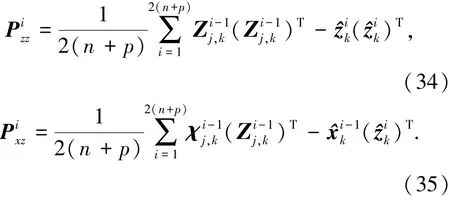
然后计算第i次迭代的滤波增益、状态估计及方差估计分别为

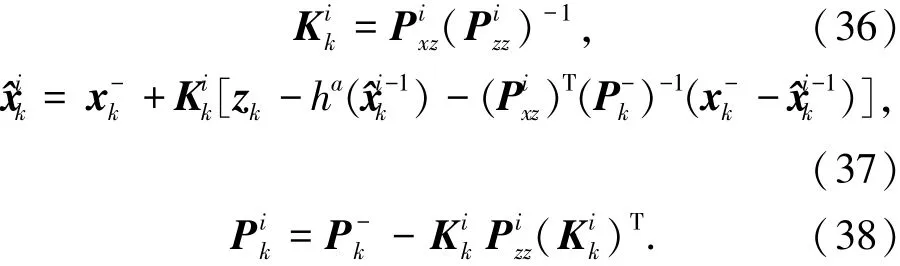
从上述方法可以看出，量测噪声经过扩维参与整个运算，能够很好地解决状态估计在更新迭代后与量测噪声相关的问题，提高估计精度，但是相对于ICKF，通过状态扩维将容积点从原来的2n个变为2（n+p）个，同时每次迭代都要进行均方根运算，引入了大的计算量，因此，为了在保证估计精度的前提下，降低计算量，本文提出一种通过容积点进行迭代的策略，避免每步迭代中都采用均方根计算来产生容积点，这样能够提高量测更新的实时性．

2.2.2 容积点迭代策略

文献［9-11，14］中建立的迭代更新函数都是以状态为变量来进行迭代的，通过高斯近似来求取采样点.为此，本文根据文献［16］中无迹回归非线性数据一致理论，建立关于容积点的迭代更新函数

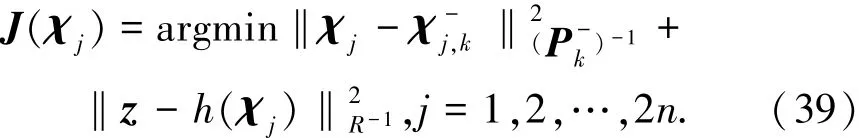
式中:z为量测值；χj为需要求的迭代容积点．

迭代更新函数是关于2n个容积点的独立最优问题，为了求解该问题，采用Gauss-Newton迭代理论可以求得

则式（32）变换为

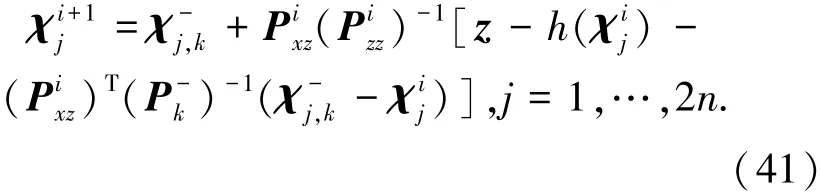
式（40）为量测方程线性化后得到的结果，这种线性化引入了高阶的截断误差，如果量测方程的非线性程度较高，那么会引起较大的传递误差，影响估计精度.因此需要采用精度较高的容积数值积分理论近似量测的方差Pizz以及协方差Pixz．式（41）为容积点迭代策略，可以看出容积点可以直接进行迭代更新，而以往的迭代策略都是通过对状态进行迭代，然后通过高斯假设以及平方根的运算来求取容积点，这样就增加了计算量．

2.2.3 IICKF算法

将容积点的迭代策略、扩维理论以及CKF算法相结合，提出了一种精度更高的IICKF算法，算法步骤如下.

1）时间更新．根据式（13）～（16）得出一步预测的状态和方差

3）求取扩维后的容积点

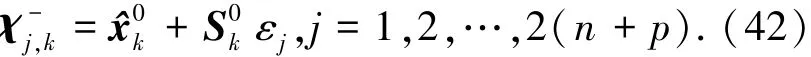
计算第i次迭代容积点经量测方程的传递值为

计算第i次迭代的量测预测、新息方差及协方差分别为

计算第i次迭代的容积点以及方差分别为

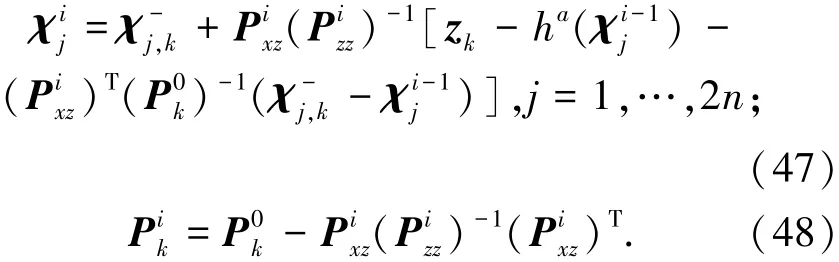
4）迭代终止条件.通过容积点计算第i次迭代的状态估计为

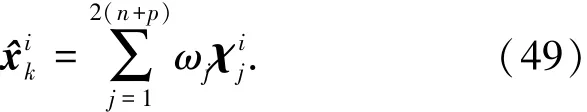
迭代终止条件为

设迭代终止时的迭代次数为N，则k时刻的状态估计与方差估计为

2.3 IICKF姿态估计算法实现

设采样时间为Δt，采用四阶龙格库塔法将式（10）、（11）所示的非线性连续系统离散化，有

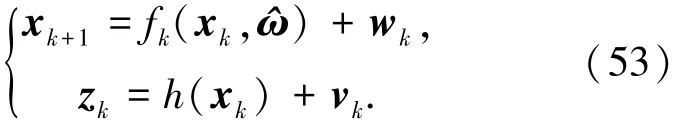
则基于IICKF姿态估计算法具体流程如下.

1）设tk-1时刻系统的状态估计值为x＾k-1以及状态协方差阵Pk-1，则利用IICKF算法得到tk时刻的状态估计x＾k和状态协方差阵Pk．

3）再利用以上步骤，不断循环，实时地估计系统状态，并进行校正，从而求得姿态及陀螺漂移信息.

3 仿真与分析

本文以捷联惯导／星敏感器姿态估计系统为平台，主要包括航迹仿真、捷联惯性导航系统、星敏感器仿真、滤波系统等.仿真初始条件设置:假设载体初始位置为北纬45°，东经126°，高度为0，初始航向角为90°，初始横滚角和俯仰角都为0°，速度为0；仿真时间为600 s；陀螺测量噪声σv= 0.05°／h，陀螺漂移噪声σu=0.003°／h，输出频率为100 Hz；星敏感器测量噪声σs=18″，输出频率为1 Hz；初始陀螺漂移β=［1°1°1°］T／h；初始姿态角误差设定为［0.5°0.5°15°］T；初始姿态与陀螺漂移的估计值均设为0；初始方差阵分别设为（0.2°）2I3×3和（1.2°／h）2I3×3．

为验证算法的有效性，采用MEKF算法、文献［15］的ICKF算法以及本文的IICKF算法进行仿真实验.由捷联惯导工具箱生成一条载体的运动轨迹，如图1所示，轨迹包括滑跑、加速、爬高、转弯等，然后对应该轨迹由星敏感器等产生相应的仿真信号，进行仿真.仿真结果见图2～4.

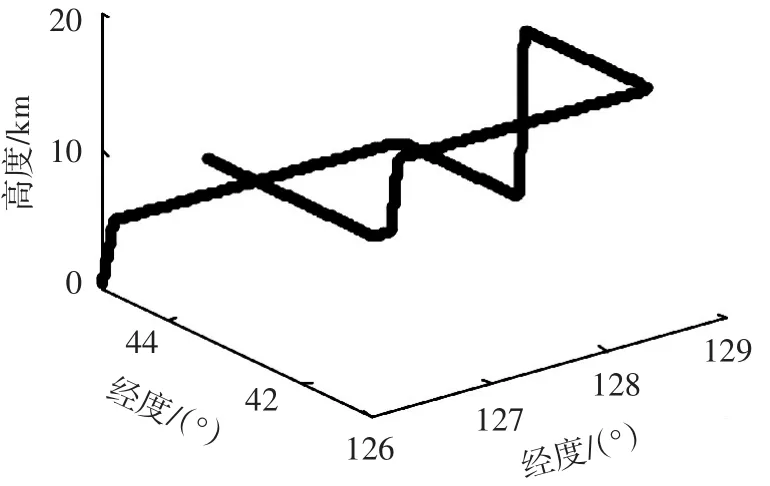
图1 载体运动轨迹

图2 横滚角姿态误差

图3 俯仰角姿态误差

图4 偏航角姿态误差

由图2～4可以看出，IICKF和ICKF的估计精度以及收敛速度始终高于MEKF算法，而IICKF算法与ICKF算法的收敛速度相当，这是因为IICKF和ICKF算法都是以CKF算法为基础，其精度以及收敛速度都要高于EKF算法.比较IICKF算法和ICKF算法，从表1可以看出，IICKF算法的估计精度要高于ICKF算法，这是由于ICKF在量测每步迭代后会造成状态与量测噪声相关，影响估计精度，而IICKF算法则是采用将噪声与状态扩维，解决了量测迭代后状态与量测噪声相关的问题，能够提高估计精度.同时也可以看出IICKF算法一次迭代时间略高于ICKF算法，这是由于在量测更新阶段，虽然采用了状态与量测噪声扩维的方法，容积点由原来的2n个变为2（n+p）个，但是新的容积点迭代策略的应用，避免了每次迭代都进行均方根运算，有利于提高实时性.

表1 3种滤波算法性能对比

4 结 论

1）在分析现有迭代滤波策略存在问题的基础上，在量测更新中，用状态扩维理论解决每步迭代后存在状态与量测噪声相关的问题，提出一种新的容积点迭代策略，直接进行容积点的迭代，避免了传统迭代策略中容积点都是通过高斯近似以及平方根运算的局限，可以降低扩维带来的计算量.

2）通过将新的容积点迭代理论与CKF算法相结合，利用容积数值积分理论近似非线性函数的均值和方差，并将其应用于由星敏感器和陀螺组成的姿态估计系统中，通过仿真实验验证了提出的算法能够有效地提高姿态估计的精度.

［1］LEFFERTS E J，MARKLEY F L，SHUSTER M D. Kalman filtering for spacecraft attitude estimation［J］. Journal of Guidance Control and Dynamics，1982，5（5）:417-429.

［2］AHMADI M，KHAYATIAN A，KARIMAGHAEE P. Attitude estimationbydivideddifferencefilterin quaternion space［J］.Acta Astronautica，2012，75（1）:95-107.

［3］TANG Xiaojun，LIU Zhenbao，ZHANG Jiasheng. Square-root quaternion cubature Kalman filtering for spacecraft attitude estimation［J］.Acta Astronautica，2012，76（1）:84-94.

［4］乔相伟，周卫东，吉宇人.用四元数状态切换无迹卡尔曼滤波器估计的飞行器姿态［J］.控制理论与应用，2012，29（1）:97-103.

［5］BELL B M，CATHEY F W.The iterated Kalman filter update as a Guass-Newton method［J］.IEEE Trans on Automatic Control，1993，38（2）:294-297.

［6］JULIER S J，UHLMANN J K，DURRANT-WHYTE H F.A new method for the nonlinear transformation of means and covariances in filters and estimators［J］. IEEE Transactions on Automatic Control，2000，45（3）:477-482

［7］SIBLEY G，SUKHATME G，MATTHIES L.The iterated sigma point Kalman filter with applications to long range stereo［C］／／Proceedings of the Robotics:Science and Systems.Philadelphia:［s.n.］，2006.

［8］ZHAN Ronghui，WAN Jianwei.Iterated unscented Kalman filter for passive target tracking［J］.IEEE Tran on Aerospace and Electronic Systems，2007，43（3）: 1155-1163.

［9］程水英，毛云祥.迭代无味卡尔曼滤波器［J］.数据采集与处理，2009，24（增1）:43-48.

［10］程水英，余莉.迭代无味卡尔曼滤波器的算法实现与应用评价［J］.系统工程与电子技术，2011，33（11）:2546-2553.

［11］WANG Changyuan，ZHANG Jing，MU Jing.Maximum likelihood-based iterated divided difference filter for nonlinear systems from discrete noisy measurements［J］.Sensors，2012，12（1）:8912-8919.

［12］ARASARATNAM I，HAYKIN S.Cubature Kalman filter［J］.IEEE Transactions on Automatic Control，2009，54（6）:1254-1269.

［13］ARASARATNAM I，HAYKIN S，HURD T R.Cubature Kalman filtering for continuous-discrete systems:theory and simulations［J］.IEEE Transactions on Signal Processing，2010，58（10）:4977-4993.

［14］穆静，蔡远利.迭代容积卡尔曼滤波算法及其应用［J］.系统工程与电子技术，2011，33（7）:1454-1457.

［15］MARKLEY F L.Attitude error representations for Kalman filtering［J］.Journal of Guidance，Control，and Dynamics，2003，26（2）:311-317.

［16］VACHHANI P，NARASIMHAN S，RENGASWAMY R. Robust and reliable estimation via unscented recursive nonlinear dynamic data reconciliation［J］.Journal of Process Control，2006，16（1）:1075-1086.

（编辑 魏希柱）

Attitude estimation based on improved iterated cubature Kalman filter

QIAN Huaming，HUANG Wei，SUN Long
（College of Automation，Harbin Engineering University，150001 Harbin，China）

To make use of the latest measurement information sufficiency，and to improve the accuracy of attitude estimation，based on the analysis of the current iterated filtering strategy，an improved iterated cubature Kalman filter（IICKF）is presented in this paper by combining a new cubature points iterated strategy with cubature Kalman filter.The filtering algorithm uses the cubature numerical integration theory to calculate the mean and variance of the nonlinear function，utilizing the state augmented method to solve the issue that the state is correlated with the measurement noise in the iterated process.A new cubature points iterated strategy is developed，which can directly iterate the cubature points，and thus avoids to generate cubature points by calculating the mean-squared root.It overcomes the limitation that sampling points are produced by the Gauss approximation in the traditional iterative strategy，which can reduce computational complexity. Simulation results show that IICKF is superior to multiplicative extended Kalman filter and iterated cubature Kalman filter in precision，which indicates that it can help to improve the accuracy of attitude estimation.

attitude estimation；improved iterated cubature Kalman filter；cubature numerical integration theory；state augmented method；precision

U666.12

A

0367-6234（2014）06-0116-07

2013-05-21；

2014-05-20.

国家自然科学基金资助项目（61104036）；哈尔滨市科技创新人才研究专项基金项目（RC2014XK009013）.

钱华明（1965—），男，教授，博士生导师.

黄 蔚，huangwei2393＠163.com.