水平管油-水两相管流的流型判别及压降预测＊

娄晨 彭清华 林棋

（1.中国石油大学（北京）油气管道输送安全国家工程实验室；2.中国石油塔里木油田分公司油气运销部）

水平管油-水两相管流的流型判别及压降预测＊

娄晨1彭清华2林棋1

（1.中国石油大学（北京）油气管道输送安全国家工程实验室；2.中国石油塔里木油田分公司油气运销部）

在总结国内外学者对油-水两相流的不同流型划分方法的基础上，结合油-水管流特性，将水平管内中／低黏度油-水两相流的流型划分为：油包水分散流、水包油分散流、油水分层流、间歇流四种流型，并建立流型转换准则和理论压降计算程序，对其进行基础性、实验散点数据、整体流型划分及压降计算检验。流型判别及压降预测结果和实验数据能很好地吻合，可为油田集输管路的设计和安全运行提供借鉴，避免由于管道泄漏引发的环境污染。

油-水两相流；水平管；流型；压降

0 引 言

随着国内大量油田生产进入中后期，原油含水率增高，以及勘探开采向深水、海洋领域的拓展，油-水两相流广泛存在于油田集输管网中。研究油-水两相流的流动规律及准确的摩阻压降预测，对于油田集输管道的经济设计和安全运行有着指导性作用。在管道底部，水相受重力作用部分聚积成分离层，加剧管道内部的结垢与腐蚀。通过对流型的控制，将水相以液滴分散于油相中，可极大减缓腐蚀，降低管道因腐蚀穿孔而导致的泄漏，避免因管道泄漏引起的周边地区环境污染及人员伤亡事件。此外，通过流型控制，可成倍地降低压降损耗，同时提高输油效率。因此，研究油-水两相管流具有非常重要的意义。

国内外众多学者对油-水两相流流型进行了分类，由于所选取油品的物性、实验环境条件、观测流型方法的不同，所观测的流型存在差异［1］。本文旨在建立一套流型判别和压降预测的计算程序，为防止输油管道腐蚀泄漏，保证油田集输管网安全、环保、高效的运行提供理论指导。

1 油-水两相流流型判别及压降计算模型

参考Taitel和Dukler气液流型划分方法，将油-水两相流型划分为：油包水（W／O）分散流、水包油（O／W）分散流、油水分层流、间歇流四种流型。

1.1 分散流

1.1.1 稳定条件

油水分散流要能稳定存在，连续相必须处于紊流，并且紊流能打碎分散液滴，足够克服液滴与液滴之间的聚并而转换到其他流型。由流体流动引起的最大液滴直径应当小于保持球形液滴时的临界直径：

临界直径公式：

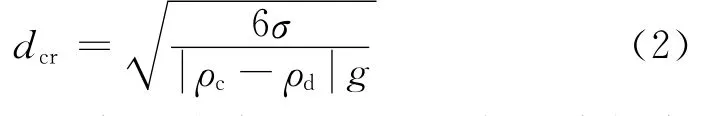
式中，σ为油水界面表面张力，N／m；ρc为连续相密度，kg／m3；ρd为分散相密度，kg／m3。

计算最大液滴直径的三种方法如下。

方法1：先利用牛顿迭代法求平均直径d32，见式（3）。

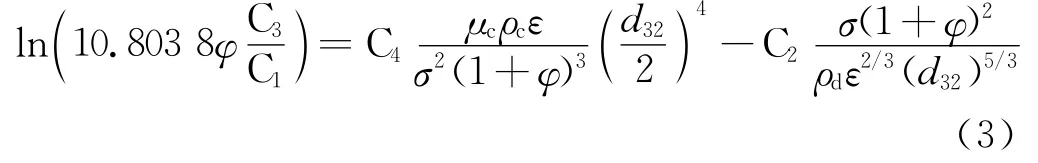
式中，Ci为常数项；φ为入口含水率；μc为连续相的动力黏度，Pa·s；d32为平均直径，m；ρd为分散相密度，kg／m3；ε为连续相能量损耗率。根据dmax＝d32／k（k的值取0.4～0.6）可计算dmax。

方法2：

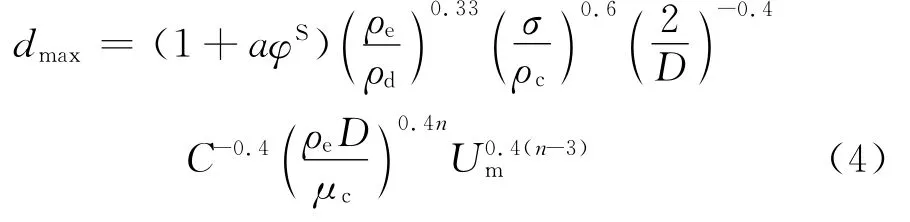
娄晨，中国石油大学（北京）油气储运工程专业在读硕士，研究方向：油气管道输送相关技术。通信地址：北京市海淀区志新西路3号中国石油规划总院海外规划研究所917室，100083式中，a＝1.65，s＝0.5，C＝0.046，n＝0.2为经验常数项；1＋aφ（）s为内相浓度的函数；D为管道直径，m；μc为连续相的动力黏度，Pa·s；Um为混合物流速，m／s。

方法3：

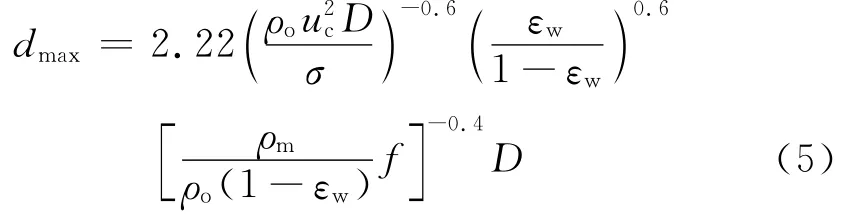
式中，uc为连续相的流速，m／s；εw为入口含水率；ρo为油相密度，kg／m3；ρm为油水均相混合物密度，kg／m3；f为摩擦因子；D为管道直径，m。

将上述三种方法求出的最大直径与临界直径相比较，进行分散流流型判别［2］。

1.1.2 压降预测

分散流是油-水两相水平管流动中一种常见的流型。本文将油-水两相流视作均相流对其进行压降的预测，运用单相流动方程来计算分散流的压降［3］。

当Rem≤1 500，层流的混合摩擦因子计算式：

当Rem＞1 500，紊流的混合摩擦因子计算式：

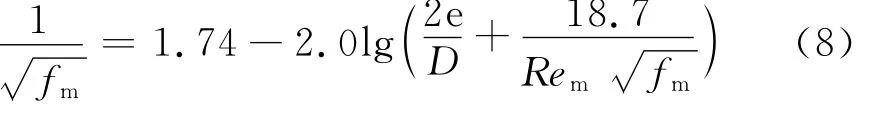
计算混合物雷诺数，关键在于选择合适的混合物有效黏度。有效黏度是分散相浓度的函数，而与混合流速基本无关。同时，连续相的黏度对于混合物的黏度起主要影响。因此，本文分别选用Taylor方程式和陈家琅有效黏度关系式来计算O／W和W／O分散液的有效黏度，见式（9）～（10）。

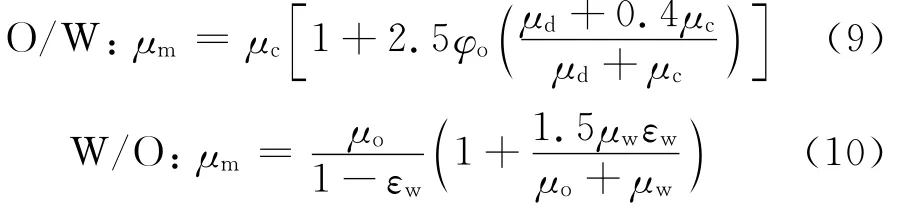
1.2 分层流

1.2.1 稳定性条件

Brauner和Maron在1992年推导出了液-液分层流的线性稳定分析。在这个分析中，包含了由于波的曲率产生的界面张力的影响。通过稳定性分析得出了两条转换线，即零中性稳定线（zero neutral stability）和零真实特性线（zero real characteristics）［4］。运用这两条线来预测分层光滑流向其他流型转变的准则。基于Kelvin-Helmholtz（K-H）不稳定性理论和与临界振幅相关的波长，Angeli博士提出了液-液分层流动保持稳定和不稳定的转换模型，该模型可很好地预测流型，见式（11）～（16）。

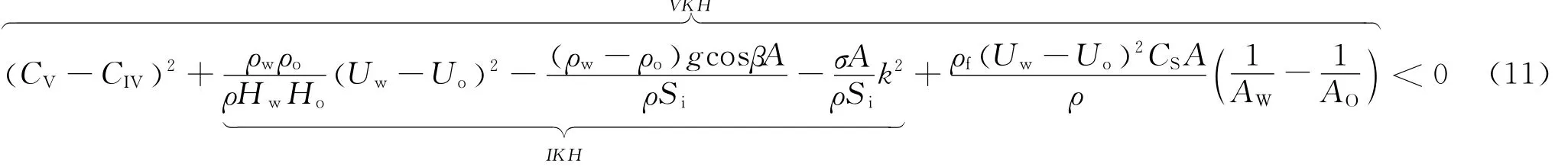
其中：

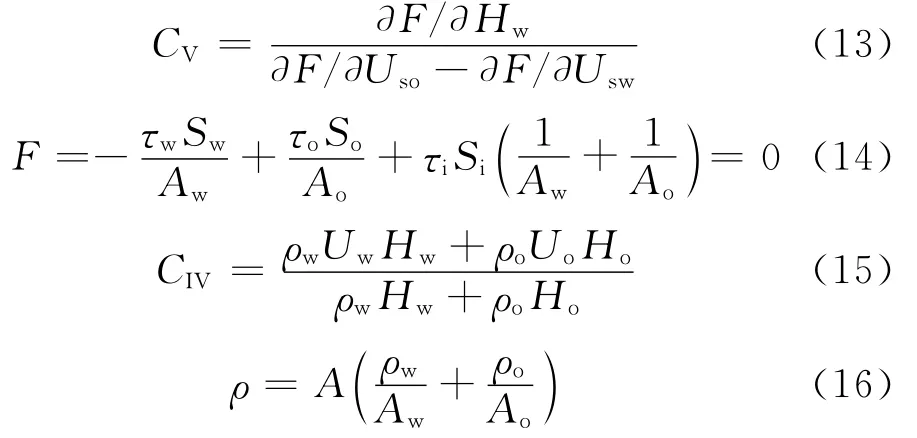
式中，Hw，Ho分别为当地截面含水率和截面含油率，%；Usw，Uso分别为水、油的折算速度，m／s；Uw，Uo分别为水、油的实际平均流速，m／s；τw，τo，τi分别为水相、油相与壁面之间的摩擦应力以及界面摩擦应力，N／m2；Sw，So，Si分别为水相、油相和油水界面的润湿周长，m；CV，CIV分别为界面波波速、临界界面波速，m／s。

1.2.2 压降预测

油水分层流动时，流动相对比较稳定，可以将所研究的管流假定为一维稳态流动，对油层和水层分别列动量守恒方程并相加后，可以得到压力梯度的表达式，压力梯度主要包括管路流动时的水力摩阻压降及重力压力梯度两部分。

1.3 间歇流压降预测

当均不满足分层流、分散流判别准则时，将此时流型定义为间歇流。对于间歇流的压降计算，总的思路是认为油-水两相还是分层，建立两相的动量方程，其中计算一相中夹带另一相的体积含量是求解的关键。液滴夹带的物理现象虽然简单，但用方程描述起来比较复杂。因此，采用Al-Wahaibi修正了的Zigrang&Sylvester摩阻系数压降相关式［5］，用于压降计算。

2 程序计算及分析

与气液流型判别类似，水平管道油水流型判别作为一个整体体系，对于任何给定的管线参数、流体物性参数、运行参数，都应能给出相应的流型判别结果。因此本文将上述判别准则进行整合，分析流程见图1。

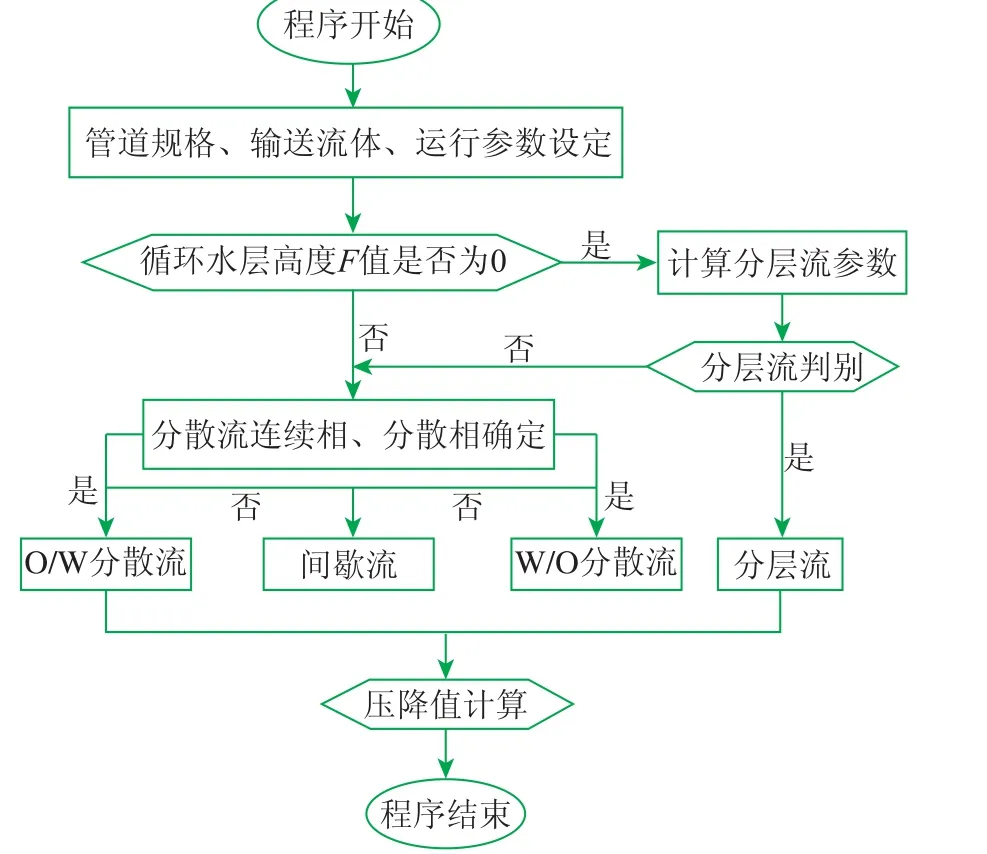
图1 程序判别流程

2.1 程序基础性分析检验

流型判别程序稳定性检验见图2。图2表明了管径对油水分层流、分散流稳定性的影响。其中管径分别为25.4 mm、50.1 mm及76.2 mm，油相的黏度为28.8 Pa·s，油水密度比为0.85，界面张力为0.036 Nm。预测表明，随管径增大，分层流的范围变宽，O／W和W／O分散流的范围变窄。大管径中的油-水两相流动更易出现分层流型，是因为此时重力稳定项的作用更为明显，在一定程度上能够克服界面波的增长，并且有更大的流通面积使两相各自能稳定流动。同时，小管径里油水流动分散的比较均匀，这是因为相同混合流速下能量耗散率和紊流动能越大；此外，在相同管径和内相浓度时，维持均匀O／W分散流型的混合流速要大于W／O分散流型。此程序计算分析结果与实际情况相符。

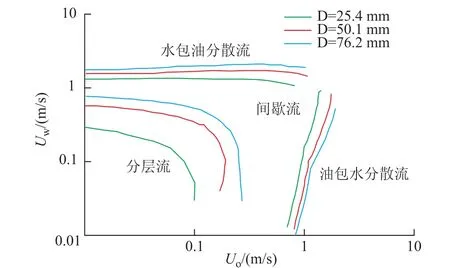
图2 流型判别程序稳定性检验

2.2 陈杰博士实验数据点程序检验

为验证程序计算可靠性，选取陈杰博士实验数据［6］中关于分层流（ST、ST&MT）、W／O分散流、O／W分散流的部分数据进行程序流型判别，并与其原实验结果进行对比，分析程序判别计算的可靠性。实验主要相关参数：①油品物性参数：油品密度为856 kg／m3，油品黏度为0.062 8 Pa·s；②水的密度为1 000 kg／m3，水黏度为0.001 Pa·s；③管道直径：0.026 1 m。

陈杰博士实验数据程序判别检验见图3。由图3可得：在数据点检验中，程序判别检验结果与原文结果基本一致。在分层流（ST、ST&MT）、W／O分散流、O／W分散流所选取的数据中，程序检验与原文吻合度较高（相同结果达80%以上）。其中判别不符的数据点基本都是在流型转化边界区，边界区的数据点本身就存在着一定的不稳定性，对离散数据点程序检验是可靠的。

2.3 流型图划分及实验压降计算程序检验

在调研大量国外水平管内油-水两相流流型的基础上，选择具有代表性的Trallero流型图［7］及Oglesby实验压降数据［8］，分析程序绘制出的流型图与Trallero流型图的相似度，以及程序计算压降值与Oglesby实验压降数据的误差大小，从而实现对程序流型划分及压降计算准确性的检验，见图4、图5。

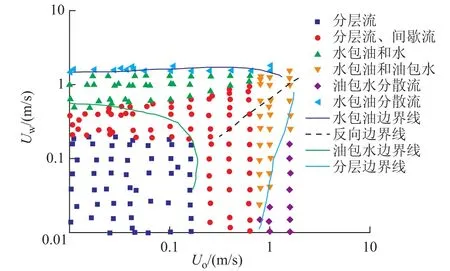
图4 程序流型划分与Trallero实验数据对比

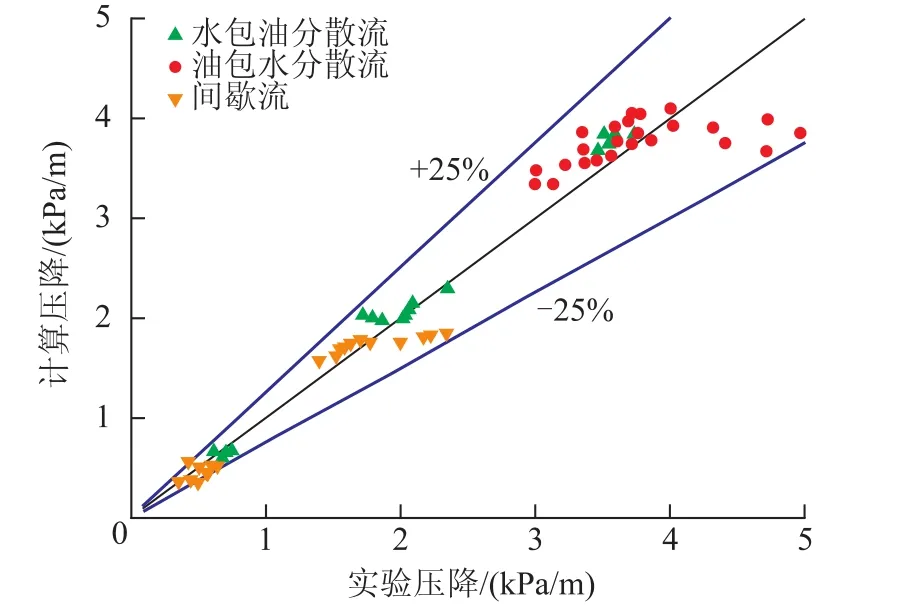
图5 程序压降预测与Oglesby实验数据对比

图4 结果显示：分散流（O／W，W／O）的预测结果较好；实验中出现的界面略有混杂的分层流型范围很大，程序预测到的分层流型范围包括部分界面混杂的分层流，这主要是因为有机玻璃管实验材料亲油性比较强，容易出现分层和过度混合等分离流型。图5结果表明：大部分的预测值与实验值的偏差在±25%以内，其中预测误差相对较大的为W／O实验点。

3 结 论

◆为使物理现象更为清晰，便于建立数学模型。考虑油水管流特性，结合Taitel和Dukler气液流型划分方法，将水平管油-水两相管流划分为：油包水分散流、水包油分散流、油水分层流、间歇流四种流型。

◆针对所建立的流型判别及压降计算程序，进行基础性检验、实验散点数据检验、整体流型划分效果及压降计算的验证，结果表明程序可靠、准确。

◆通过对水平管油-水两相流流型的判别与压降计算，可实现对管内流体流型控制，进而有效地防止管路结垢、腐蚀和产生水合物等现象。在长距离高黏原油的多相输送中，可实现成倍降低摩阻压降及提高输油效率。

［1］ 姚海元,宫敬.水平管内油水两相流流型转换特性[J].化工学报,2005,56(9):1649-1653.

［2］ Brauner N.The Prediction of Dispersed Flows Boundaries in Liquid-liquid and Gas-liquid Systems[J].International Journal of Multiphase Flow,2001,27(5):885-910.

［3］ Oglesby K D.倾斜管油－水两相流实验研究[R].张劲军,译.北京:中国石油天然气总公司信息研究所,1993.

［4］ Brauner,Maron.Stability Analysis of Stratified Liquidliquid Flow[J].International Journal of Multiphase Flow,1992,18(1):103-121.

［5］ Al-Wahaibi T,Angeli P.Transition between Stratified and Non-stratified Horizontal Oil-water Flows.Part I: Stability Analysis[J].Chemical Engineering Science, 2007,62(11):2915-2928.

［6］ 陈杰，孙红彦，严大凡.水平管内油水两相流流型的实验研究［J］.油气储运，2000，19（12）：27-30.

［7］ Trallero.Oil-water Flow Pattern in Horizontal Pipes [D].Tulsa:University of Tulsa,1996.

［8］ Oglesby K D.An Experimental Study on the Effects of Oil Viscosity,Mixture Velocity and Water Fraction on Horizontal Oil Water Flow[D].Tulsa:University of Tulsa,1979.

1005-3158（2014）02-0012-04

国家科技重大专项课题资金资助项目（2011ZX05039-002、2011ZX05039-004-006）。

2013-11-28）

（编辑 李煜）

10.3969／j.issn.1005-3158.2014.02.005