人工神经网络与多元统计判别分析在古陶瓷断源断代中的对比研究

吴 隽，尹 丽，张茂林，吴军明，李其江

（景德镇陶瓷学院，江西 景德镇 333001）

人工神经网络与多元统计判别分析在古陶瓷断源断代中的对比研究

吴 隽，尹 丽，张茂林，吴军明，李其江

（景德镇陶瓷学院，江西 景德镇 333001）

针对古陶瓷断源断代的研究目的，以景德镇仿龙泉青瓷与龙泉青瓷胎的化学组成为研究对象，选择了多元统计判别分析方法、人工神经网络算法对其进行数据处理分析和产地判别研究，并将多元统计判别分析和人工神经网络进行对比分析，探讨了不同方法之间的差异性及适用性。结果表明，由于古陶瓷元素组成数据难以完全满足多元统计判别分析对于数据变量的要求，因而多元统计判别分析相对于人工神经网络的判别正确率较低，人工神经网络更适合用于古陶瓷断源断代研究。

古陶瓷；断源断代；BP人工神经网络；多元统计分析；判别分析

0 引 言

关于古陶瓷断源断代的探索一直是古陶瓷科技研究的热门课题之一，主要是通过测试分析已知年代、产地古陶瓷标本的胎釉元素组成，经各种数据分析方法处理，找出其时代和地域特征，进而将未知年代、产地古陶瓷标本的胎釉元素组成与之对比，即可探索出未知标本的年代和产地[1]。

近年来，随着现代科学技术与数据分析方法研究的发展，越来越多的数据处理方法在古陶瓷断源断代的研究领域中得到了广泛应用，其中较为传统的多元统计判别分析在国内外的使用最为普遍，此外，人工神经网络等方法因其应用智能化比较适合无明确数学表达式的体系，在古陶瓷的研究与鉴定当中也逐渐崭露头角[1]。然而，古陶瓷元素组成数据有其自身的特点，且不同的数据分析方法对古陶瓷数据的统计分布需求常常也有所不同，例如多元统计判别分析要求各个判别变量符合正态分布，以及变量不能是其他判别变量的线性组合等。那么，针对古陶瓷元素组成数据的特点，进行断源断代研究时如何选择更为适合的数据分析方法显然非常重要，但未见相关研究报道。

另一方面，龙泉窑是我国古代生产青瓷最具代表性的窑口之一，其青瓷产品已成为不同地区广大窑工争相效仿的对象，并以景德镇明清时期仿制最具代表性，且二者在外观上较为接近，传统鉴定方法比较难以区分。因此，本文试图通过对景德镇仿龙泉青瓷与龙泉青瓷进行产地判别分析，来探索BP人工神经网络与多元统计中的判别分析在古陶瓷断源断代数据分析中应用的特点，通过对比分析这两种数据处理方法在古陶瓷断源断代研究中的实际应用，探讨了不同数据分析方法之间的差异性及适用性，便于学者根据数据的自身特点和条件，选择更具可靠性和准确性的方法来达到数据分析的目的，为提高不同数据分析方法在古陶瓷断源断代中的合理利用提供了一定的参考依据。

1 实验样品及数据

本文分析研究了25件景德镇仿龙泉青瓷及龙泉青瓷样品(典型样品见图1)，其中包括景德镇仿龙泉青瓷样品7件(FLQ-1～FLQ-7)，龙泉青瓷样品18件(LQ-1～LQ-18)，采用能量色散X荧光光谱仪测试了样品胎体的化学组成，数据如表1所示。

2 数据分析与讨论

2.1 人工神经网络分析

人工神经网络是人们试图模拟人的神经系统的结构, 并获得神经系统的功能而设计的一类计算方法，由许多作为基本结构单位的神经元(processing element, PE)组成。所有神经元的相互连接处都被赋予一个权重值，信息进入神经元之前都经过加权计算，其相关原理见文献[1-6]。

以表1中的8个主、次量元素数据为样品的特征变量，构成一个8维模式空间。分别将景德镇仿龙泉青瓷与龙泉青瓷的产地归类用(1,0)和(0,1)表示，并选取其中的10件样品数据作为预测集，其中景德镇仿龙泉青瓷3件(FLQ-3，FLQ-5，FLQ-7)，龙泉青瓷7件(LQ-2，LQ-3，LQ-5，LQ-7，LQ-8，LQ-13，LQ-17)。

采用MATLAB 7.0.1软件编写神经网络程序，以胎的主、次量元素化学组成数据进行编写。所建立的人工神经网络分为输入层、输出层和隐蔽层[7-10]。其中输入层有8个神经元，分别对应于所测试的8个元素含量。输出层有2个神经元，分别对应景德镇仿龙泉青瓷、龙泉青瓷。隐蔽层和输入层的转换函数采用常用的sigmoid函数：f(u)=1/(1+e-u)，这个函数值域在0～1之间。网络输出t=(t1; t2)，然后将输出值与期望值相比较，期望值y分别是(1,0)，(0,1)，分别代表景德镇仿龙泉青瓷，龙泉青瓷的样品。在训练过程中希望实际输出值和期望值之间的差别尽可能地小，即要不断调整权重向量，使越来越小。

图1 部分典型样品的外观照片Fig.1 The appearance of some typical samples

本文从25个样品中挑选出15个样品作为训练集，剩下的10个样品作为测试集。使用经过训练的人工神经网络对剩下的样品进行判别归类，正确率达100%。

由此可见，用于模式识别的BP人工神经网络能完全区分出景德镇仿龙泉与龙泉两个产地的瓷片，识别准确率近100%。

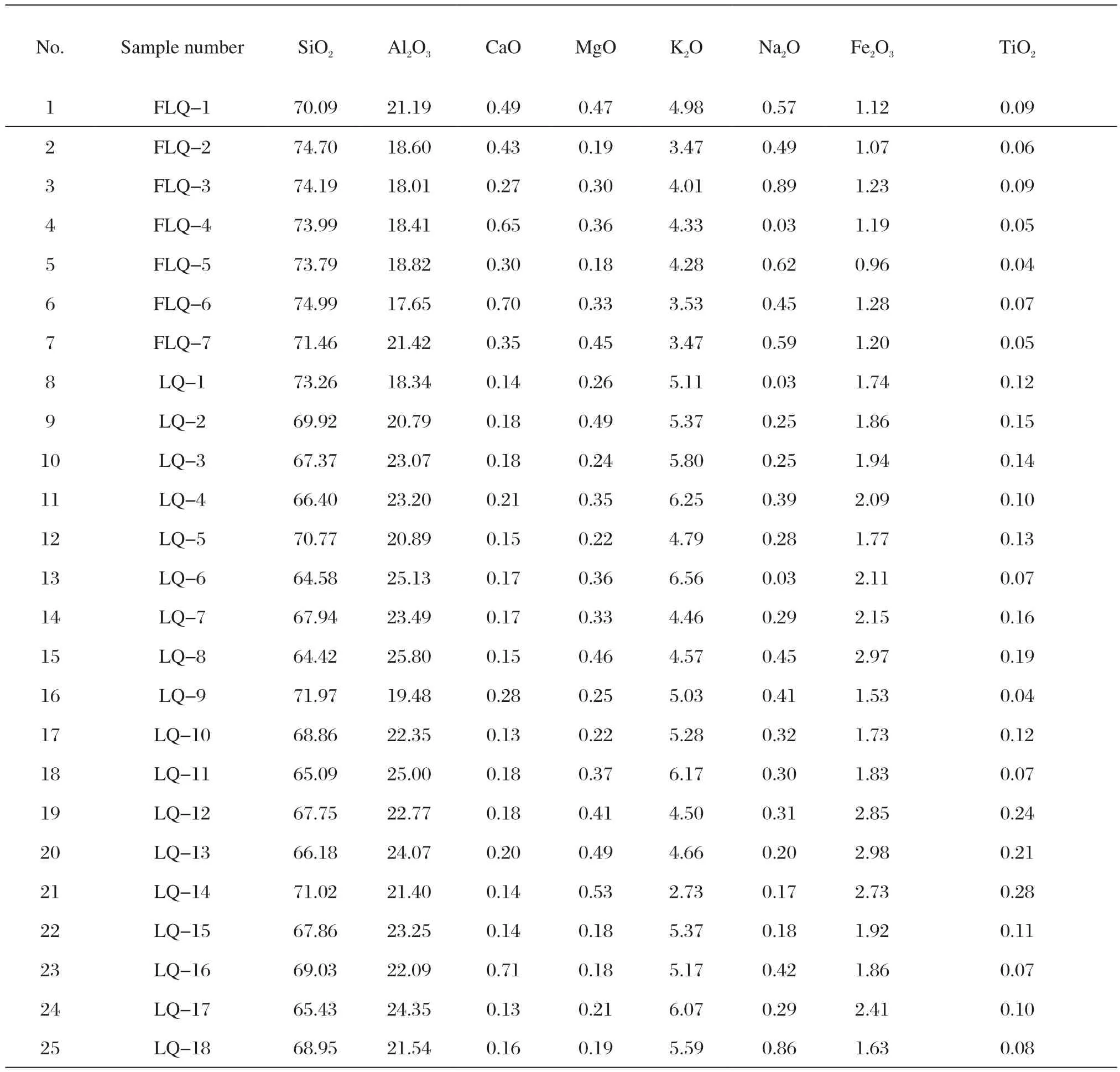
表1 景德镇仿龙泉青瓷与龙泉青瓷胎的主、次量元素化学组成 /wt.%Tab.1 Chemical composition of body major and minor elements of Jingdezhen imitated Longquan and Longquan celadon /wt.%

2.2 判别分析

判别分析是根据观察或测量到的若干变量值判断研究对象如何归类的方法，即在己知分类数目的情况下，根据一定的指标对不知类别的数据进行归类的多元统计方法。用SPSS 13软件对胎的主、次量元素组成做判别分析。判别分析的方法选为Fisher判别法建立全模型，假设各类样本先验概率相等，并指定使用合并组内协方差矩阵进行分类[11-15]。

判别分析结果如表3。

由表3可知判别得分与自变量之间的相关系数，表中上标“a”表示该元素不适用于数据分析，因此“Fe2O3”元素不参与判别函数的建立。

通过Fisher多级判别分析求得判别函数为：

Y1=2377.457SiO2+2589.667Al2O3+1826.395CaO +3118.739MgO+2328.259K2O+1959.556Na2O+ 14372.481TiO2-118522

Y2=2372.140SiO2+2584.535Al2O3+1815.704CaO +3086.386MgO+2327.926K2O+1948.428Na2O+14435.481TiO2-118025

根据判别函数对原样本进行归类，景德镇仿龙泉青瓷与景德镇龙泉青瓷的判别正确率为96.0%。由表4的回代判别法检验结果可知，有一个龙泉青瓷被误判为景德镇仿龙泉青瓷。

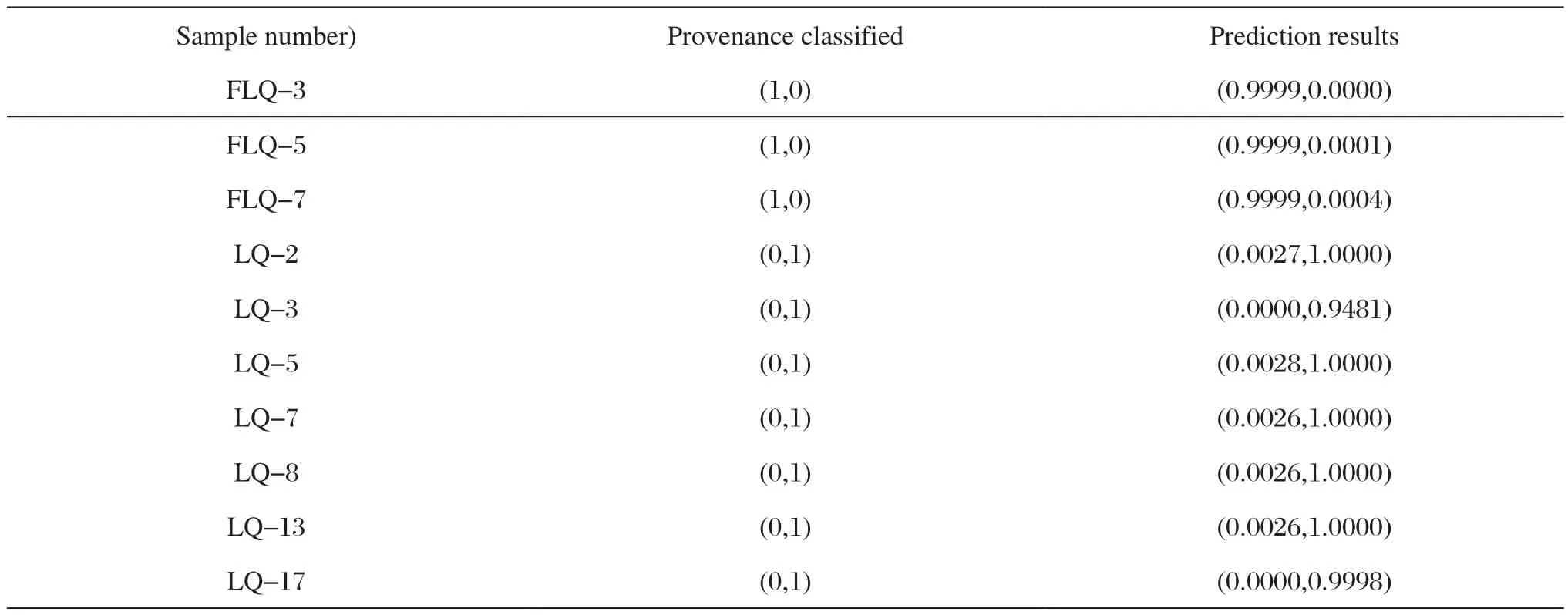
表2 人工神经网络预测结果Tab.2 The prediction results of ANN

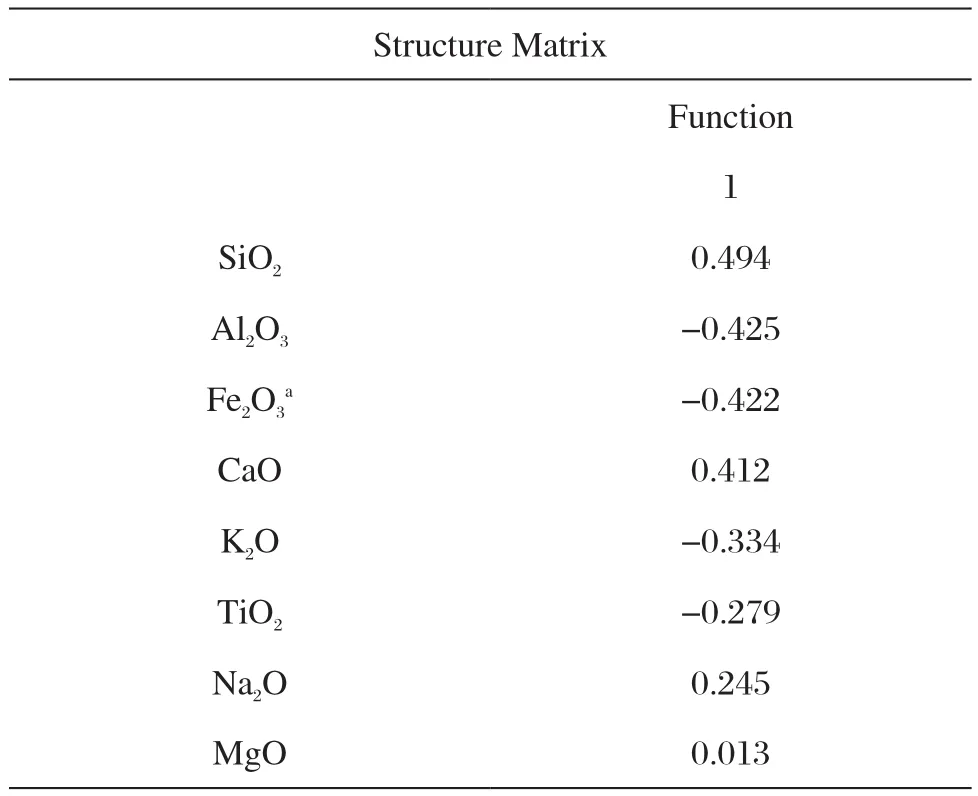
表3 结构矩阵(胎)Tab.3 Structure matrix(bodies)

2.3 人工神经网络与多元统计判别分析的对比分析

由表2与表4可知，人工神经网络相对于多元统计分析而言，对景德镇仿龙泉青瓷与龙泉青瓷产地判别的准确性较高。

表4 回代判别法检验结果(胎)Tab.4 The test results of back substitution method (bodies)

造成以上差异的主要原因可以归纳为以下几点：

(1)在多元统计方法的判别分析中，变量选择的好坏会直接影响判别的效果，一般来说，原始变量在判别函数中的作用是不同的，有的意义重大，有的作用很小。而将判别能力很小的变量留在判别函数中，会增加计算量，甚至会干扰判别结果。而在这一点上，人工神经网络的模式识别由于神经网络分类器一般对输入模式信息的不完备或特征的缺损不太敏感，即使局部或部分的神经元不准确或损坏后，也不会对全局的活动造成很大影响，具有非常强的容错性。因此相对受变量选择的影响较小，从而在最终判别结果的准确性上具有一定的优势。

(2)多元统计判别分析要求假定各个判别变量不能存在多重共线性，即每个判别变量不能是其他判别变量的线性组合。然而以古陶瓷元素组成中的氧化硅与氧化铝为例，其相关性分析如表5和表6所示。

由表5和表6可知，景德镇仿龙泉青瓷与龙泉青瓷的SiO2和Al2O3的相关系数分别为-0.945和-0.967，均属于高度相关，其显著性p分别为0.001和0.000均小于0.01具有统计学意义，由此可见古陶瓷元素组成中的部分变量是线性相关的，这也是造成传统多元统计判别分析误差较大的原因之一。

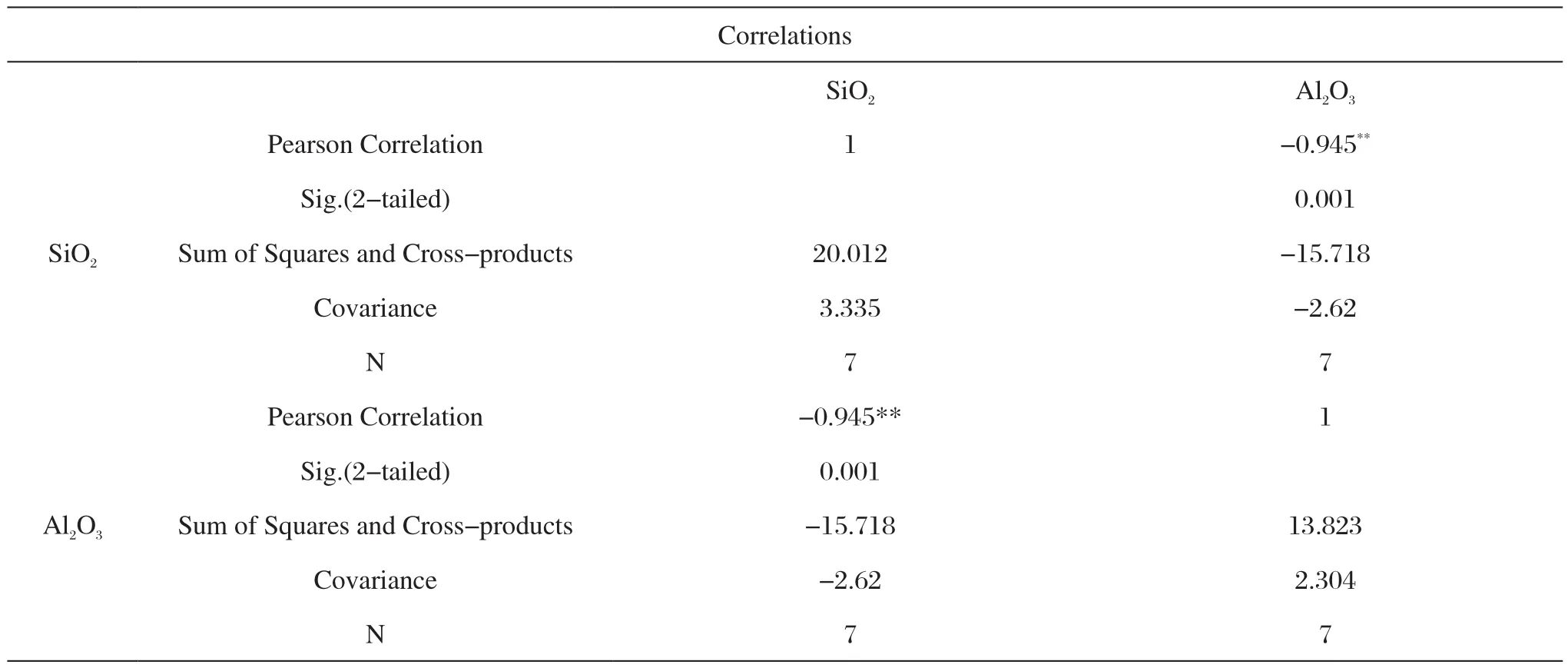
表5 景德镇仿龙泉青瓷中SiO2与Al2O3相关性分析Tab.5 Correlation analysis of SiO2and Al2O3in Jingdezhen imitated Longquan celadon

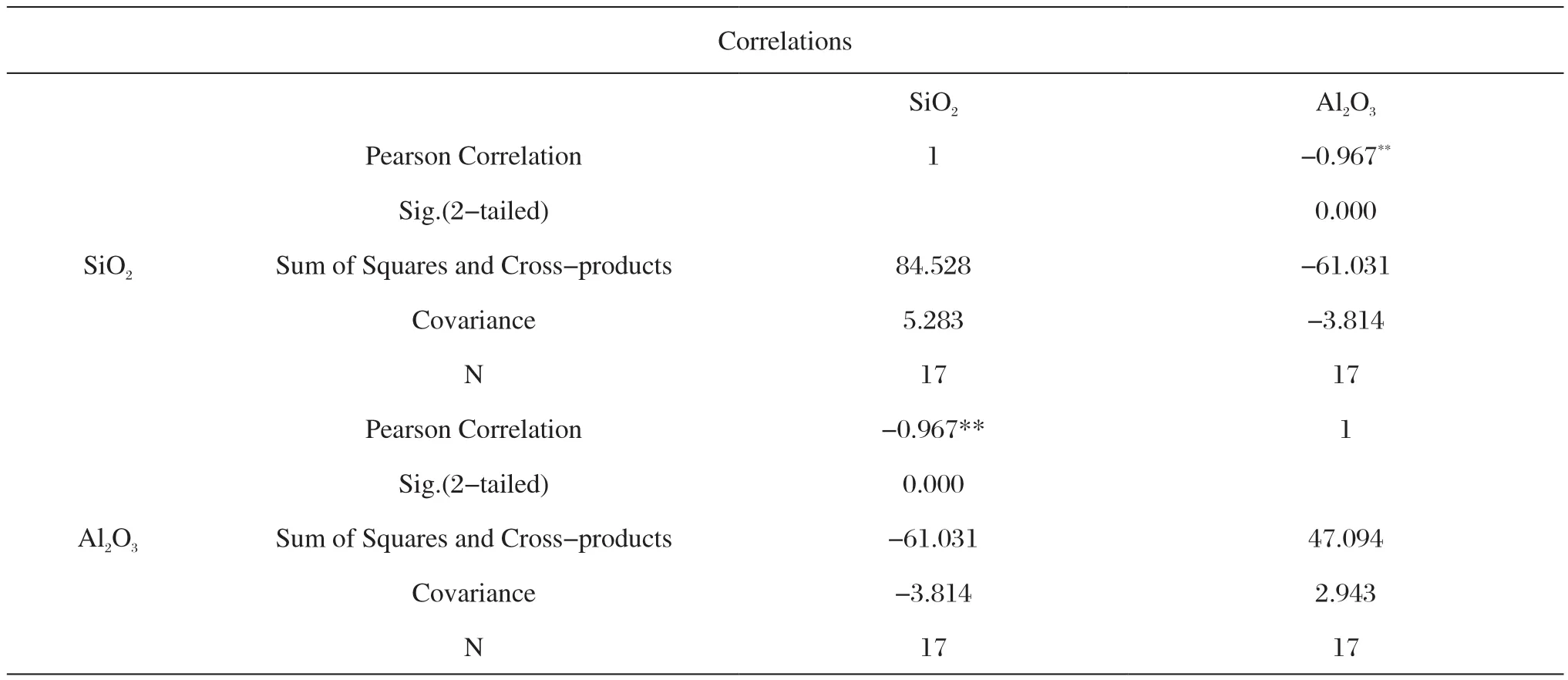
表6 龙泉青瓷中SiO2与Al2O3相关性分析Tab.6 Correlation analysis of SiO2and Al2O3in Longquan celadon

(3)古陶瓷化学组成数据为连续性数据，多元统计分析中的判别分析是通过建立判别函数对其进行判别归类，其前提假设是各个判别变量需服从正态分布，由各个判别变量的联合分布是多元正态分布。只有在这个条件下，才可以进行有关的显著性检验；然而在实际情况中，根据古陶瓷的数据特点，其各个变量不一定全部符合正态分布，常常是部分符合，以龙泉青瓷中的CaO为例，采用SPSS 13软件对其数据进行正态分布讨论。

常规下，符合正态分布的曲线如图2所示。

龙泉青瓷CaO正态分布曲线如图3所示，其中横坐标为CaO含量，纵坐标为分数出现的频数。

由图2和图3可知，直方图绘出的曲线与常规的符合正态分布的曲线出入较大，为了结果更具可靠性，对其进行正态分布检验。

检验方法一：

Q-Q图检验，所得结果如图4所示。

由图4可知，在Q-Q图中，各点中的大部分围绕直线的紧密程度较为松散,其中一个离直线距离较远，说明数据呈正态分布的可能性较小。

检验方法二：

单个样本K-S检验，检验结果如表7所示。

由表7可知，在K-S检验中，sig.即P值=0.022＜0.05，没有达到正态分布的标准。

图2 正态分布曲线Fig.2 Normal distribution curve

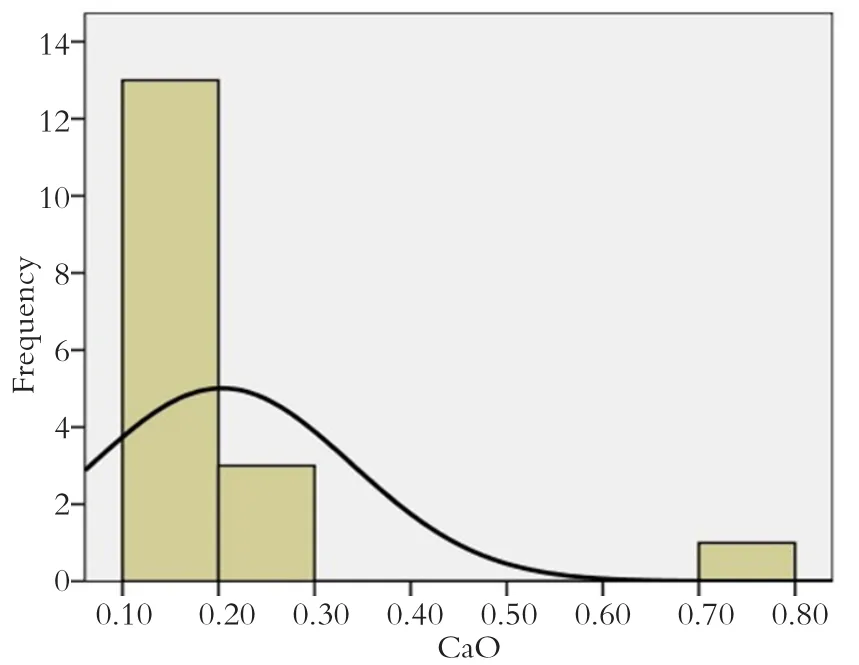
图3 龙泉青瓷CaO正态分布曲线Fig.3 Normal distribution curve of CaO in Longquan celadon

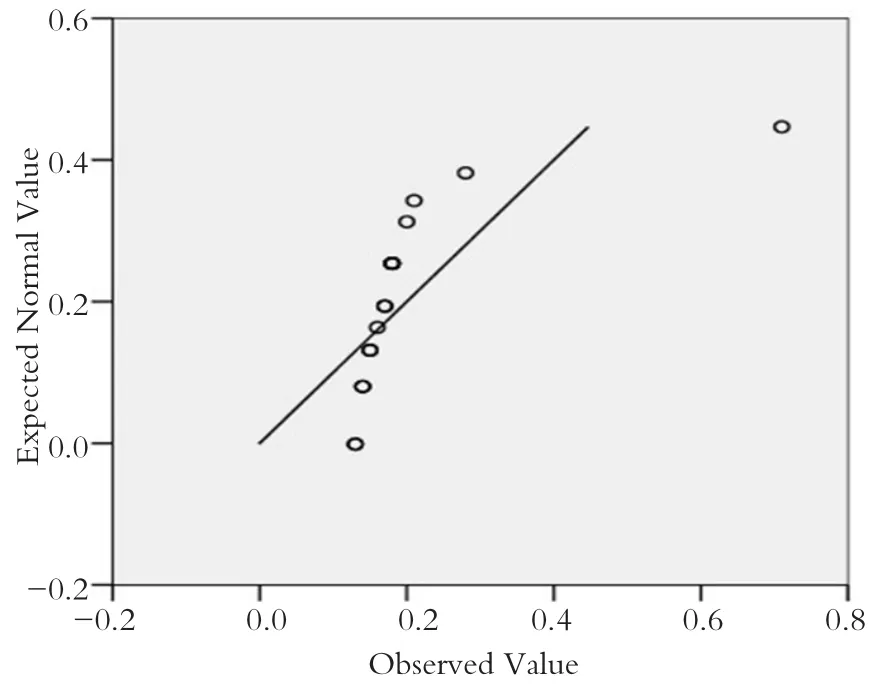
图4 龙泉青瓷CaO正态分布检验结果Fig.4 Normal distribution test results of CaO in Longquan celadon

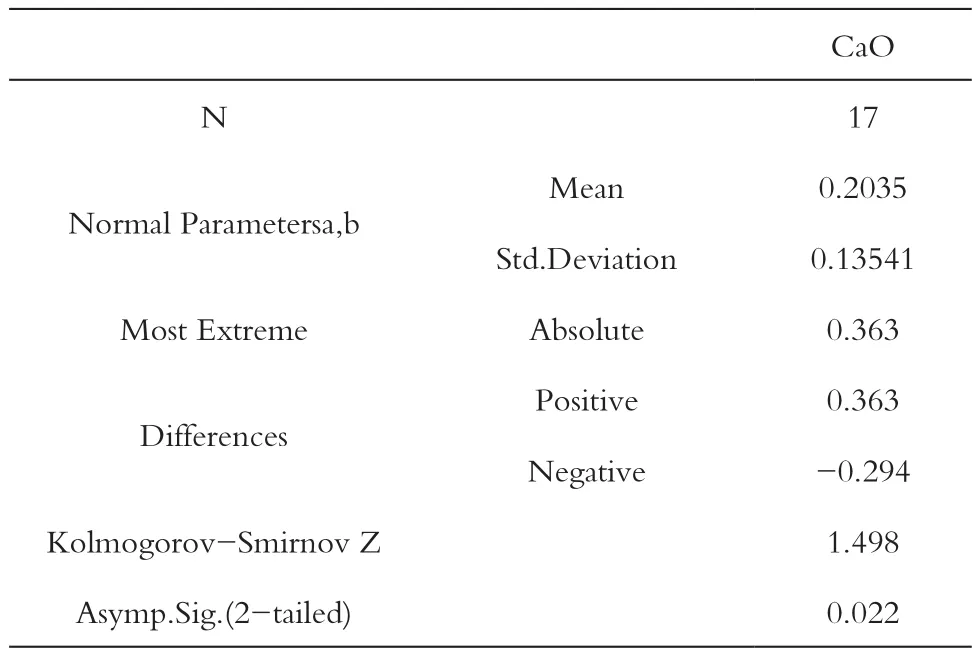
表7 龙泉青瓷CaO正态分布检验结果Tab.7 Normal distribution test results of CaO in Longquan celadon

综合上述检验结果基本可以确定CaO并不服从正态分布。由此可见，古陶瓷的数据并不满足多元统计判别分析中要求各个数据完全符合正态分布的假设。然而，与进行数据分析的多元统计方法不同，人工神经网络的模式识别对所要求的处理对象在样本空间的分布状态无需作任何假设，而是直接从数据中学习样本之间的关系，从空间趋于划分和从样本属性着眼进行分析，因而是一种非函数的几何方法，具有自组织和自学习能力，其着眼点并不在于完整地复制，而是抽取其中可利用的部分来克服其他系统不能解决的问题，如学习、控制、识别等。

(4)人工神经网络具有一些多元统计分析所不具备的优势，比如神经网络的推广能力，神经网络的模式变换和模式特征提取作用，以及神经网络的高度并行特点可使大量相似或独立的运算得以同时进行，从而使其在处理问题时比传统的数据处理器具有更快的速度。

6 结 论

通过对龙泉青瓷和景德镇仿龙泉青瓷胎的元素组成的数据分析，比较多元统计判别分析和人工神经网络的差异性和适用条件，研究发现：

(1)多元统计判别分析所建立的判别函数对龙泉青瓷和景德镇仿龙泉青瓷标本的判别正确率为96.0%，基本达到相关断源断代的目的。其判别正确率相对不高的原因主要是古陶瓷数据并非完全符合正态分布以及古陶瓷元素之间常高度相关，这两点使其不满足判别分析的前提假设。

(2)人工神经网络对景德镇仿龙泉青瓷与龙泉青瓷两个产地瓷片的判别正确率为100%，高于多元统计判别分析，说明人工神经网络更适合做产地判别分析。其原因主要与人工神经网络对变量的识别具有较强的容错性以及它不要求假定样本服从多元统计分析需要服从的一些统计分布等有关。

[1] 吴隽,张茂林,李其江,吴军明.陶瓷科技考古[M].北京:高等教育出版社, 2012:191-217.

[2] 董和泉, 邓文华, 许华勇, 等. 人工神经网络在古陶瓷研究中的应用[J]. 陶瓷学报, 2005, 26(4): 280-281.

DONG Hequan, et al. Journal of Ceramics, 2005, 26(4): 280-281.

[3] 印春生, 邱平, 王昌燧, 等. 人工神经网络在古陶器产地研究中的应用[J]. 科学通报, 2000, 45(19): 2019-2112.

YIN Chunsheng, et al. Chinese Science Bulletin, 2000, 45(19): 2019-2112.

[4] 宁青菊, 于成龙, 田清泉. 人工神经网络在陶瓷材料中的应用[J]. 材料导报, 2008, 22(8): 64-67.

NING Qingju,et al, Materials Review, 2008, 22(8): 64-67.

[5] 黄国兴, 李琳, 李冰, 等. 人工神经网络在材料制备工业中的应用[J]. 材料导报, 2006, 20(11): 80-83.

HUANG Guoxing, et al. Materials Review, 2006, 20(11): 80-83.

[6] 周少华, 付略. 古陶瓷EDXRF分析及数据处理方法的研究[D].浙江: 浙江大学, 2008: 55-64.

[7] Delores M.Etter,David C.Kunciciky,Holly Moore.MATLAB 7及工程问题解决方案[M].北京：机械工程出版社,2006:125-189.

[8] 郭景康,陈念贻.古陶瓷分类研究中的模式识别人工神经网络方法[J].硅酸盐学报,1997，25(5):614-617.

GUO Jingkang, CHEN Nianyi. Journal of The Chinese Ceramic Society, 1997, 25(5): 614-617.

[9] 耿冠宏,孙伟,罗培.神经网络模式识别[J].软件导刊, 2008,7(10):81-83.

GENG Guanhong, et al. Software Guide, 2008, 7(10):81-83.

[10] 张德丰.MATLAB神经网络仿真与应用[M].北京:电子工业出版社,2009:23-136.

[11] 李家治,罗宏杰.浙江地区古陶瓷工艺发展过程的研究[J].硅酸盐学报,1993，21(2):143-148.

LI Jiazhi, et al. Journal of The Chinese Ceramic Society, 1993, 21(2): 143-148.

[12] 胡祎, 吴姗姗, 胡真. 基于陶瓷原料质量评价的多种统计分析方法的比较研究[J]. 景德镇陶瓷, 2010, 20(4): 13-14.

HU Yi, et al. Jingdezhen' s Ceramics, 2010, 20(4): 13-14.

[13] 罗宏杰. 中国古陶瓷与多元统计分析[M]. 北京:中国轻工业出版社, 1997: 23-98.

[14] 罗应婷, 杨玉娟. SPSS统计分析从基础到实践[M]. 北京: 电子工业出版社, 2010: 78-152.

[15] 陈希镇,曹慧珍. 判别分析和SPSS的使用[J]. 科学技术与工程, 2008, 8(13):3567-3574.

CHEN Xizhen, et al. Science Technology and Engineering, 2008, 8(13):3567-3574.

Comparison between Artifcial Neural Networks and Multivariate Statistical Discriminant Analysis Applied to Ancient Ceramic Provenance and Chronology

WU Jun, YIN Li, ZHANG Maolin, WU Junming, LI Qijiang
(Jingdezhen Ceramic Institute, Jingdezhen 333001, Jiangxi, China)

The chemical composition test results of the body of Jingdezhen imitated Longquan and Longquan celadon were studied by multivariate statistical discriminant analysis and artifcial neural networks for their respective provenance and chronology. The differences and applicability of the two methods were discussed. Results show that as the data of ancient ceramic element composition couldn’t fully meet its requirements, the accuracy of the multivariate statistical discriminant analysis is lower than that of the artifcial neural networks, which means the artifcial neural networks is more suitable for ancient ceramic provenance and chronology determination.

ancient ceramics; provenance and chronology; BP artifcial neural network; multivariate statistical analysis; discriminant analysis

date: 2014-03-17. Revised date: 2014-04-05.

TQ174.4

A

1000-2278(2014)04-0429-07

10.13957/j.cnki.tcxb.2014.04.017

2014-03-17。

2014-04-05。

国家自然科学基金青年项目(编号：11205073)；国家文物局文化遗产保护科学与技术研究课题(编号：20110104)；新世纪优秀人才支持计划资助。

吴 隽(1969-)，男，博士，教授。

Correspondent author:WU Jun(1969-), male, Ph. D., Professor.

E-mail:wj1608@sina.com