陶瓷干法造粒机叶片安装高度对造粒效果的影响

吴南星，鲍 星，廖达海，肖志锋

（景德镇陶瓷学院机电学院，江西 景德镇 333403）

陶瓷干法造粒机叶片安装高度对造粒效果的影响

吴南星，鲍 星，廖达海，肖志锋

（景德镇陶瓷学院机电学院，江西 景德镇 333403）

为了分析陶瓷干法造粒机叶片安装高度对造粒效果的影响，该文基于欧拉—欧拉模型建立数学模型，利用有限体积法求解，模拟研究了造粒过程中颗粒的体积分布情况。结果表明：当叶片与造粒室底端最小距离为15 mm时，颗粒的分散性最好，造粒效果最佳。

叶片；欧拉-欧拉模型；数值模拟；分散性

0 引 言

目前陶瓷干法造粒装备制得的颗粒存在表面形状不规则、颗粒实心、颗粒硬度大[1,2]等缺陷，这会导致成形过程容易分层、坯体强度偏低、坯体表面粗糙等[3,4]现象。

陶瓷干法造粒机制得的颗粒存在的各种缺陷，很大程度是因为在造粒过程中颗粒没有得到足够的分散。而叶片对颗粒的分散性[5]具有决定性作用。本文正是认识到叶片对颗粒分散性的重要，对此建立数学模型对造粒过程进行数值仿真分析。本文的研究成果对陶瓷干法造粒技术的积累和改进具有一定的参考价值。

1 数学模型

造粒室内粉体颗粒体积初始量约占造粒室体积的1/4，粉体颗粒可作拟流体相处理，所以本文选用欧拉—欧拉模型中的Eulerian模型来模拟造粒过程。在模拟过程中，空气相与拟流体相共存并相互渗透，具有各自的速度和体积分数，并且空气相和拟流体相分别采用相应的质量守恒方程和动量守恒方程求解。

(1)质量守恒方程

空气相连续性方程为

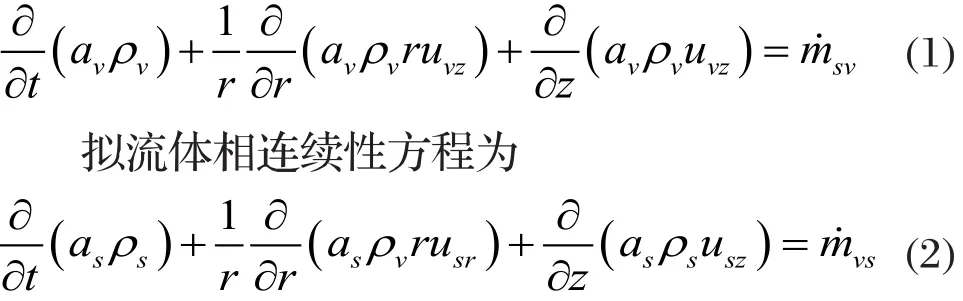
式中：avas为空气相和拟流体相的体积分数；ρv、ρs为空气相和拟流体相的密度，k g / m3；uvr、uvz为空气相的径向速度和轴向速度，m / s ；usr、usz为拟流体相的径向速度和轴向速度，m/ s；m˙sv为空气相质量增加速率，kg /(m3⋅s)，(即从拟流体相到空气相的质量速率)；为拟流体相质量增加速率，kg /(m3⋅s)(即从空气相到拟流体相的质量速率)。

式(1)、(2)中，等式由非定常项、对流项和源项组成，表示空气相与拟流体相之间的传递，并且有

(2) 动量守恒方程

空气相动量方程为

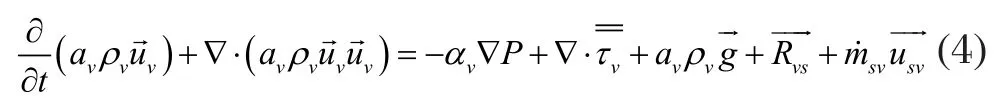
拟流体相动量方程为

Rvs、 Rsv分别为两相间曳力(且)，Rvs= - Rsv，N。Rvs矢量定义为

式中Kvs为曳力模型中气固两相间动量交换系数，kg/s。为气、固两相的雷诺应力张量(K=v,s)，N /m2，且有

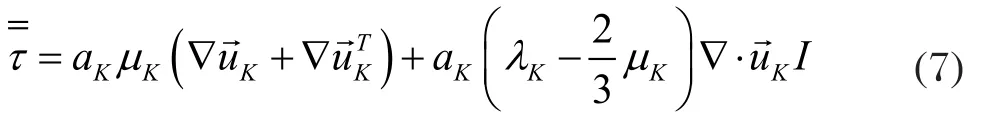
式中：λ为体积粘度系数，Pa⋅ s；μ为剪切粘性系数，Pa⋅ s；I为单位张量。

2 模型建立

2.1 模型简化

本文主要研究的是干法造粒试验机造粒过程，其造粒室简图如图1所示，颗粒在叶片、铰刀和造粒室的旋转作用下实现湿润、搅拌和造粒。造粒室基本尺寸如下：造粒室内径为φ235 mm、高为280 mm，初始加入颗粒体积占造粒室体积的1/4(约70 mm)。

2.2 物理模型及边界条件

通过造粒室简图1可建立数值模拟物理模型图2。由于叶片、铰刀结构复杂，对此本文采用SolidWorks软件绘制三维模型，再通过Gambit软件和搅拌专用前处理Mixsim软件中完善模型、划分网格及设定初步的边界条件，从而在Fluent软件中完善相关参数设定进行模型求解。具体物理模型及边界条件如图2所示，由于颗粒主要是通过叶片、铰刀的搅拌作用实现运动的，故叶片、铰刀附近区域颗粒的运动较大，而离叶片、铰刀相对较远的区域颗粒运动较小。因此把物理模型分成两部分，一部分由叶片、铰刀和其附近区域划分为动区域；剩下部分划分为静区域。边界条件设定：由于造粒过程中造粒室上端口是开放的，故将其设置为压力出口，而动区域与静区域接触面设置为交界面，其它边界面都设置为墙。

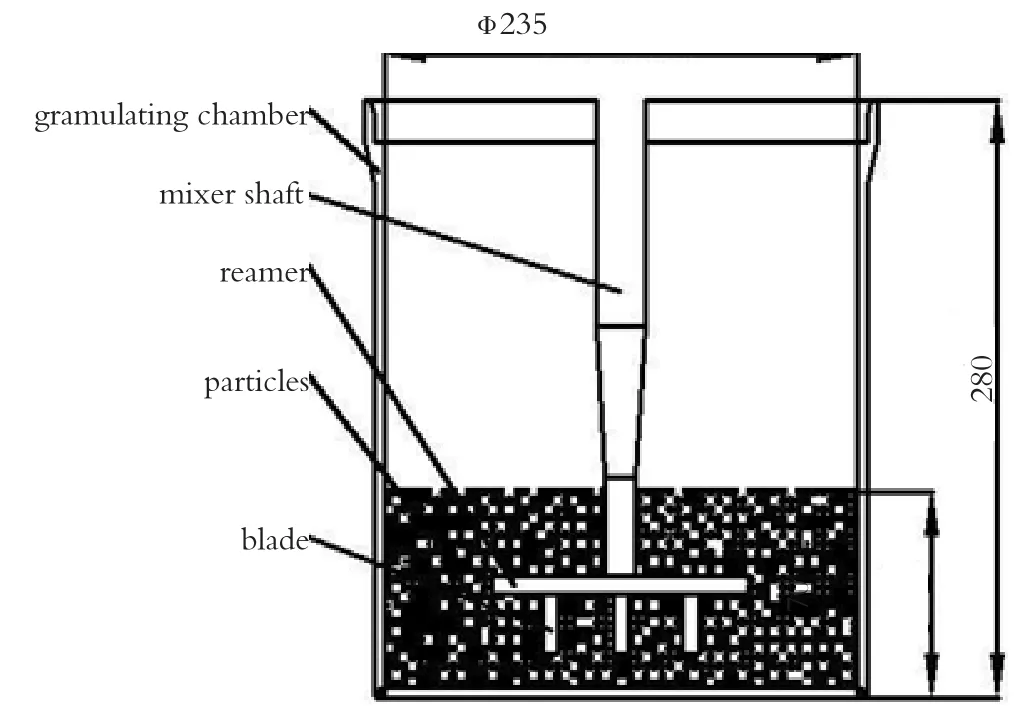
图1 造粒室简图Fig.1 Granulation chamber diagram

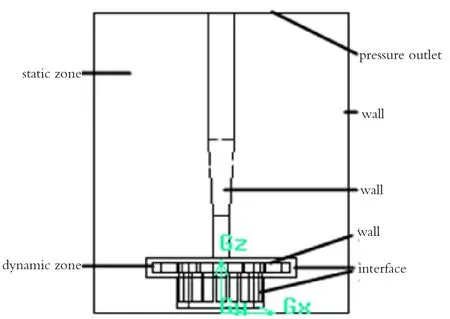
图2 物理模型及边界条件Fig.2 Physical model and boundary conditions

2.3 网格划分

本文分析的是非定常流问题，故选用滑移网格模型，将整个计算域划分为两个旋转参考坐标系，动区域为相对坐标系，采用以四面体网格为主的非结构网格划分；静区域为绝对坐标系，采用以六面体为主的非结构网格划分。其中动区域网格模型如图3所示，静区域网格模型如图4所示。

2.4 求解过程

利用Fluent基于有限体积法对控制方程组进行离散化和数值计算，在求解中采用了PC-SIMPLE算法对双流体模型进行数值迭代求解。

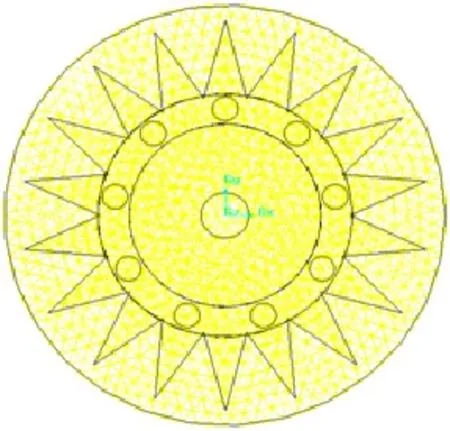
图3 动区域网格模型Fig.3 Dynamic zone mesh model

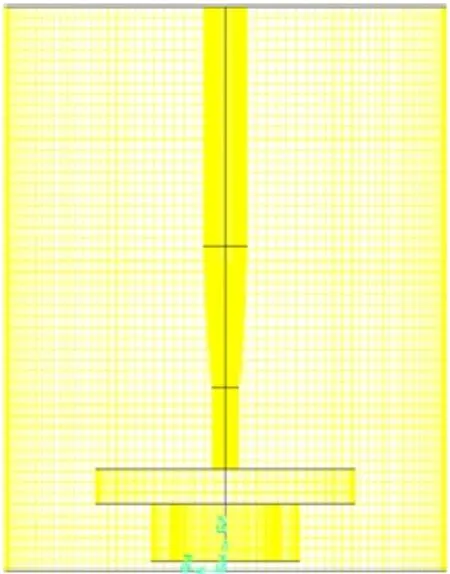
图4 静区域网格模型Fig.4 Static zone mesh model

3 结果与讨论

本文分别模拟了叶片与造粒室底端最小距离为10 mm、15 mm和20 mm的3种情况，通过模拟结果颗粒的体积分布分析颗粒的分散性。

图5为造粒过程中颗粒的体积分布剖视云图，从图中可知：当叶片安装高度为H1=10 mm时，颗粒占造粒室内体积接近50%，但是颗粒分布在堆积密度为0.45以上的区域内数量较多；当叶片安装高度为H2=15 mm时，颗粒分布在造粒室内体积大小几乎没有变化，但是颗粒分布在堆积密度为0.45以上的区域内数量减少较明显；当叶片安装高度为H3=20 mm时，颗粒分布在造粒室内的体积大小仍然没有太大的变化，但是颗粒分布在堆积密度为0.45以上的区域内数量增大较明显。因此，叶片安装高度为H2=15 mm时，造粒过程中颗粒的体积分布情况最好，即此时颗粒的充分分散性最佳，造粒效果最好。

4 数值模拟与实验数据对比分析

图6为造粒过程中数值模拟与实验数据颗粒分布在造粒室内体积大小百分比对比图。从对比图可知：随着叶片安装高度的增大，数值模拟造粒过程中颗粒的体积分布大小基本都维持在54%，实验结果造粒过程中颗粒的体积分布大小也都基本维持在45%，即数值模拟与实验数据结果相吻合，验证了数值模拟结果颗粒的体积分布大小的正确性，模型的有效性。

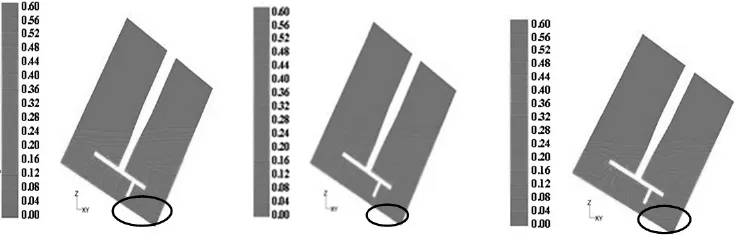
图5 颗粒的体积分布剖视云图Fig.5 Section contour for particle volume distribution

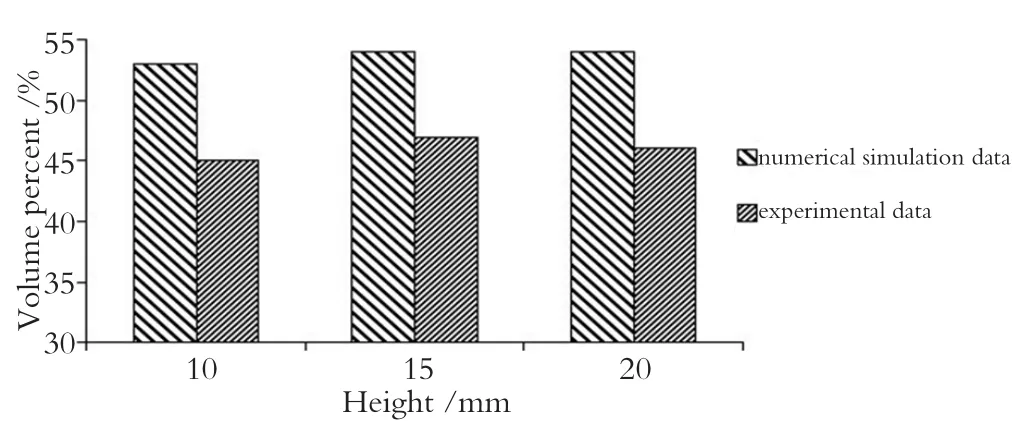
图6 颗粒体积分布大小对比图Fig.6 Particle volume distribution contrast fgure

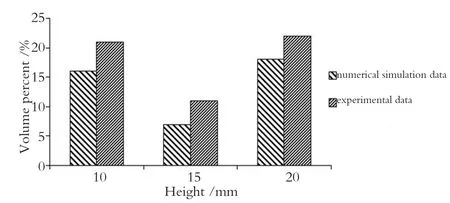
图7 颗粒堆积密度大的体积分布对比Fig.7 Large particle volume concentration contrast fgure

图7为造粒过程中数值模拟与实验数据颗粒分布在堆积度为0.45以上的区域内体积大小对比图。从对比图可知：叶片安装高度为10 mm、15 mm、20 mm时，数值模拟颗粒分布在堆积密度为0.45以上的区域内体积分布大小分别为16%、7%、18%，而实验数据颗粒分布在堆积密度为0.45以上的区域内体积分布大小分别为21%、11%、22%。即数值模拟与实验数据结果相吻合，验证了数值模拟结果颗粒分布在堆积密度为0.45以上的区域内体积分布大小的正确性，模型的有效性，也表明叶片安装高度在15 mm时达到最优值。

5 结 论

通过模拟结果从局部、直观的剖视云图分析可知，随着叶片与造粒室底端最小距离的增大，颗粒的体积分布大小基本没有变化，但是颗粒分布在堆积密度为0.45以上的区域内体积分布大小变化较大，在叶片安装高度为15 mm时达到最优值。同时通过数值模拟与实验数据对比分析，验证了模拟的可靠性，模拟结果的正确性。

综合上述可得，当叶片与造粒室底端最小距离为15 mm时，颗粒的体积分布大小、颗粒分布在堆积密度为0.45以上的区域内体积分布大小是综合最理想的，即此时造粒室内颗粒的分散性最好，造粒效果最佳。

[1] 吴南星, 廖达海, 肖志锋. 陶瓷干法造粒机的数值模拟及其优化设计[J]. 陶瓷学报, 2014, 35(2): 82-87.

WU Nanxing, et al. Journal of Ceramics, 2014, 35(2): 82-87.

[2] 张柏清, 赖泽标. 基于正交试验法对干法造粒颗粒大小影响因素的分析[J]. 陶瓷学报. 2013, 34(1): 85-88.

ZHANG Boqing, et al. Journal of Ceramics, 2013,34(1): 85-88.

[3] 李绍勇, 周荣光, 梁飞峰. 超细化干法造粒制备陶瓷粉料技术[J]. 佛山陶瓷, 2010, 08: 20-22.

LI Shaoyong, et al. Foshan Ceramics, 2010, 08: 20-22.

[4] 陶晓文. 陶瓷墙地砖干法制粉工艺技术的研究[J]. 陶瓷, 1996, 02: 11-15.

TAO Xiaowen. Ceramics, 1996, 02: 11-15.

[5] HOELLERL N, MANFREDINI U, SIKALIDIS C. Dry tech multiline: an evolution in raw materials preparation for ceramic tiles[J]. Tile & Brick International, 1994, 10(2): 93-96.

Effect of Blade Installation Height on Granulation Performance of a Dry Granulator for Ceramic Application

WU Nanxing BAO Xing LIAO Dahai XIAO Zhifeng
(School of Mechanical and Electronic Engineering, Jingdezhen Ceramic Institute, Jingdezhen 333403, Jiangxi, China)

In order to analyze the effect of the blade installation height on the granulation performance of a dry granulator, a mathematical model based on the Eulerion-Eulerion concept was established. It used the fnite volume method and simulated the particle volume distribution in dry granulation process. Results show that particles dispersion and granulation result were the best when the minimum distance between the blade and the granulation chamber was 15 mm.

blade; Eulerion-Eulerion model; numerical simulation; distribution

date: 2014-02-10. Revised date: 2014-03-08.

TQ174.5

A

1000-2278(2014)04-0415-04

10.13957/j.cnki.tcxb.2014.04.014

2014-02-10。

2014-03-08。

国家自然科学基金项目资助(编号：51365018)。

吴南星(1968-)，男，博士，教授。

Correspondent author:WU Nanxing(1968-), male, Ph. D., Professor.

E-mail:wnx1968@163.com