基于奇偶矢量的多星座RAIM算法*

李查

（西北工业大学电子信息学院，西安 710129）

基于奇偶矢量的多星座RAIM算法*

李查

（西北工业大学电子信息学院，西安 710129）

随着GNSS接收机技术的不断发展，基于多星座下的GNSS接收机自主完好性监测（RAIM）算法也已被国内外学者广泛研究。首先介绍了接收机自主完好性监测奇偶矢量算法的原理，然后分别对单星座、多星座组合下的RAIM算法进行了研究和仿真，图形化和数据化的仿真结果充分证明了多星座组合下的完好性监测性能优于单星座下完好性监测性能。

GNSS，RAIM，奇偶矢量，多星座

引言

随着GNSS接收机技术的发展，现有定位技术已能满足绝大部分用户对精度的需求；在涉及生命安全、航空航天以及导弹导航等领域，用户对定位信息的可靠性提出了更高的要求［1］。从用户安全角度考虑，导航系统的完备性比精度更重要。

完备性是导航系统发生任何故障或者误差超限，无法用于导航和定位时，系统向用户及时发出报警的能力［2］。通常完备性由以下3个指标衡量［3-4］：

（1）报警限（Alert Limit，AL）：当用户定位误差超过系统规定的某一限值时，系统向用户发出警报，这一限定值即为系统的报警限。

（2）示警耗时（Time To Alert，TTA）：用户定位误差超过报警限值的时刻和系统向用户显示这一警报时刻的时间差，称为示警耗时。

（3）完备性风险（Integrity Risk，IR）：示警能力以内的用户定位误差超过报警限值和规定的示警耗时，而系统又没有向用户发出警报的机率，称为完备性风险。

算法完备性监测的算法中，接收机自主完备性监 测 （Receiver Autonomous Integrity Monitoring，RAIM）应用最为广泛。RAIM是利用接收机自身的冗余观测值进行卫星故障的检测和识别。它无需外部设备的辅助，花费较低，容易实现，在导航系统中越来越受到重视［5］。

传统RAIM算法主要根据单星座接收机提出［6］。然而随着GPS、GLONASS、Galileo等GNSS系统的现代化推进，多星座兼容的RAIM不仅必不可少，而且可利用多系统间的冗余度信息提高可靠性。在此基础上，本文主要对RAIM算法故障检测和识别原理进行分析，推导并仿真分析多星座RAIM算法，验证了多星座RAIM算法性能。

1 基本RAIM算法

普遍采用的RAIM算法是基于当前历元观测量的“快照”（Snapshot）方法，主要包括伪距比较法［7］、最小二乘残差法［8］和奇偶矢量法［9］。这3种算法等效，其中奇偶矢量法物理意义更直观，计算相对简单，已普遍采用并被美国航空无线电技术委员会第159专门委员会（RTCA SC-159）推荐为基本算法。本文采用基于奇偶矢量法的RAIM算法，下面对该算法作基本介绍。

设可见卫星数为n，用户接收机伪距观测方程为［10-11］：

其中，x是4×1的状态矢量，代表实际位置与标称位置偏差的3个分量和用户时钟偏差；y是n× 1测量矢量，其元素是每颗卫星的测量伪距与线性化点预测伪距之间的差值；H是x和y之间的n×4线性关联矩阵，前3列由相应角的余弦值组成，第4列是一个时间列；e是n×1的测量误差矢量，假设e具有相互独立的随机元素，并服从标准正态分布。则状态矢量的最小二乘估计为：

构造奇偶空间矩阵P，使其满足PH=0且PPT= In-4的条件，P可通过H矩阵的QR分解获得。由于P的特殊性质，可以生成奇偶矢量p=Py=Pe。PTP反映了观测量间的一致性，定义为检测统计量，可用于进行故障检测和识别。

1.1 单星座RAIM的故障检测

将检测量PTP对测量噪声方差进行归一化：

其中，σ2为测量噪声方差。T服从于自由度为n-4的中心和非中心χ2分布。在可视卫星数不小于5颗的情况下，给定允许误警率PFA可计算检测门限。当归一化检测量大于检测门限时，观测卫星中含有故障。

1.2 单星座RAIM的故障识别

根据标准奇偶矢量排除算法［12］，故障卫星的识别算法如下：

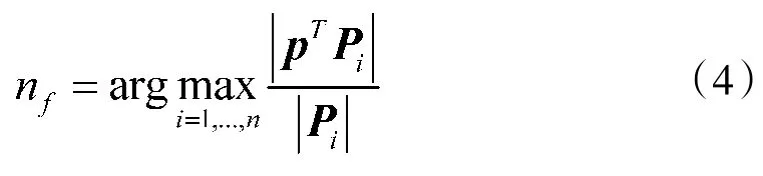
其中，nf为故障卫星号，Pi为奇偶空间矢量P的第i列。可视卫星数不小于6颗时可进行故障识别。

2 多星座RAIM算法

多星座RAIM的算法原理与单星座系统的RAIM原理基本相同。单一模式工作时，RAIM至少需要5颗可见卫星来监测异常的卫星，需要6颗以上才能辨识出故障卫星；采用双模式的RAIM，由于两种模式的卫星系统采用不同的基准时间，未知量增加了两系统的时间差，故至少需要6颗可见卫星来监测异常的卫星，7颗以上辨识出故障卫星；相应的，三模的联合解算至少需要7颗可见卫星监测异常的卫星，8颗以上辨识出故障卫星。

以GPS+GLONASS+BD三星座系统为例，n颗可见卫星情况下，伪距观测方程可写为如下形式：

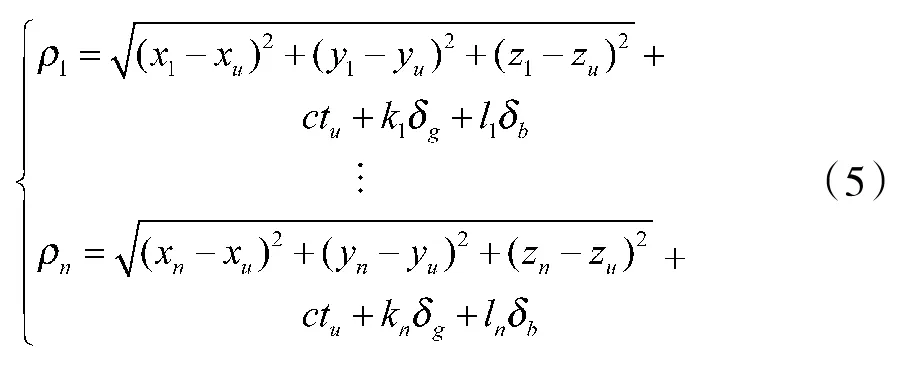
其中，ρi为第i颗卫星伪距；（xiyizi）、（xuyuzu）分别为第i颗卫星位置和所求用户位置；c为光速，tu为卫星与用户接收机之间的钟差；δg、δb分别为GLONASS、BD-2系统与GPS系统的钟差量引起的距离偏差；ki、li为系统标识位，当第i颗卫星属GPS卫星时均取0，属GLONASS系统时ki取1li取0，属BD-2系统时ki取0、li取1。对式（5）作泰勒展开，去掉高阶项，并考虑观测误差和卫星故障，多星座伪距观测方程可写为如下矩阵形式：

式中各项定义与式（1）相近，其中H∈Rn×6，最后两列为系统标识位矢量k、l，k=［k1… kn］T，l=［l1… ln］T；b是错误向量，表示由于卫星故障或者已经飞出视线引起伪距上的偏差，如第i颗卫星发生故障，则b=［0 … bi… 0］T，若无故障卫星，则b=0。

2.1 构造奇偶矢量

用户位置x的最小二乘估计为：

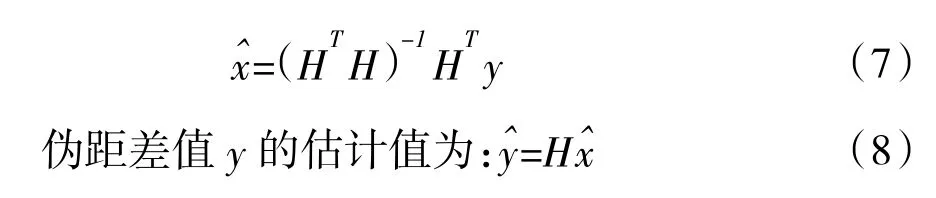
定义距离残差矢量v=y-yˆ，v中的n个元素中6个与向量x的6个未知分量相关联，这些限制会掩盖一致性方面的信息。为直接反映故障卫星的偏差信息，有必要进行变换消除这些限制因素。

对式（6）中的系数矩阵H进行QR分解，得到：

其中，Q为n×n维正交矩阵，R为n×4维上三角矩阵。先不考虑观测误差，对伪距观测模型两边左乘QT，得到：

将QT和R分别表示为：

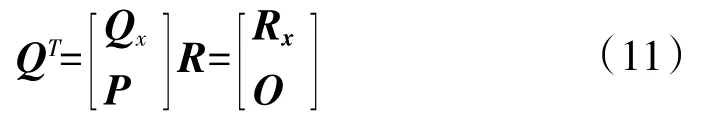
其中，Qx为QT的前6行，P为其余n-6行，Qx为R的前6行。则有：

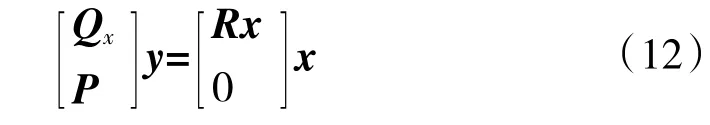
由上式可得待定参数x的解为：

现在考虑观测误差的影响，即y=Hx+e，则有：

其中，P为奇偶空间矩阵，矢量p为观测误差被奇偶空间矩阵P投影得到，一般称为奇偶空间矢量，它能直接反映故障卫星的偏差信息。具有以下性质：P的行H与的列正交；P的行相互正交；P的行都进行了标准化，每一行的大小都是单位阵。

2.2 多星座RAIM的故障检测

奇偶空间矢量p与伪距观测偏移量相关，可利用 p构造故障检测统计量。令误差项平方和SSE=pTp。若伪距误差向量e中的各个分量是相互独立的正态分布随机误差，方差为，均值为0时，依据统计分布理论，SSE/服从自由度为n-6的χ2分布；均值不为0时，SSE/服从自由度为n-6的非中心χ2分布。作如下假设检验：

多星座式下8颗星可见的χ2密度函数（2自由度）如图1所示。

2.3 多星座RAIM的故障识别

构造统计检验量ri：

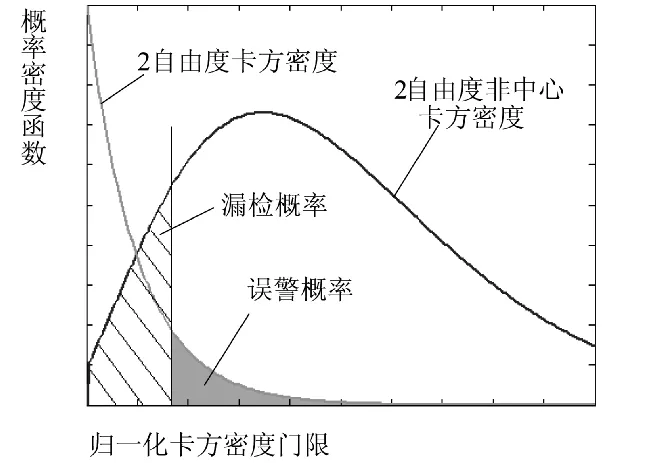
图1 2自由度的χ2密度函数

ri的物理意义见参考文献［10］、文献［13］。在无故障的情况下，ri应服从零均值的正态分布。对于给定的误警率Pfa，对n个检验统计量有：

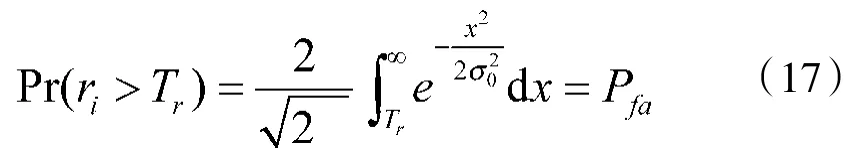
由上式求出检测限值Tr，实时比较ri与Tr，若ri＞Tr，则说明该卫星有故障。实际中可直接取令ri最大的卫星即故障卫星。

3 仿真分析

3.1 多星座RAIM的故障检测与识别

根据以上分析，本文以西安为观测点，使用STK软件对GPS、GLONASS、BeiDou系统的星座进行仿真，选取几何构型较好的8颗卫星进行定位解算，并将各卫星编号为1、2、…、8（1～4号为GPS卫星，5号～6号为GLONASS卫星，7号～8号为BeiDou卫星）。以100 ms的采样间隔采集200 s的数据，设定误警率为1/150 000，不考虑各导航系统伪距观测噪声水平不同，统一取σ0=4 m。鉴于实际中卫星导航服务完好性故障有地面运控系统故障、卫星系统故障、传播环境异常、用户接收处理故障等多种因素［14］，仿真中以脉冲型故障和阶跃型故障两种故障方式进行多星座RAIM故障检测与识别。

3.1.1 脉冲型故障

以第5颗卫星为例，在选取的观测文件的第100历元处加入幅值为10σ0的脉冲故障，使用奇偶矢量法得到的仿真结果如图2、图3所示。

图2 脉冲故障检测仿真图

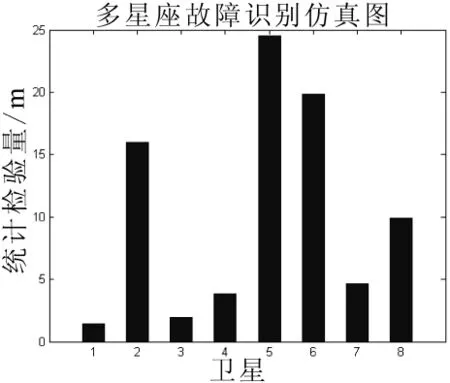
图3 脉冲故障识别仿真图

由图2，计算出的检测门限为9.88 m，仅在第100历元处出现统计检验量超出门限的情况，即此时出现卫星故障；由图3，第5颗卫星的检验量值最大，说明第5颗卫星为故障卫星，成功进行故障检测和识别。

3.1.2 阶跃型故障

仍以第5颗卫星为例，在选取的观测文件的第100至150历元处加入幅值为10σ0的脉冲故障，使用奇偶矢量法得到的仿真结果如图4、图5所示。

由图4，在第100至150历元处出现统计检验量超出门限的情况，即在这段时间内出现卫星故障；由图5，成功识别故障星为第5颗卫星。

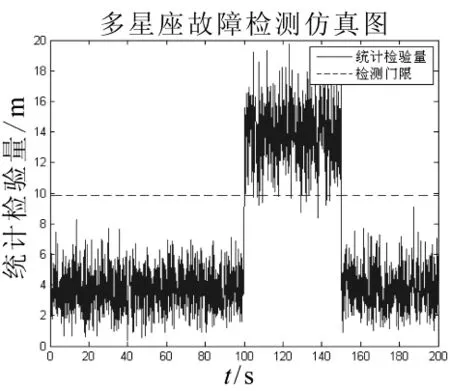
图4 阶跃故障检测仿真图

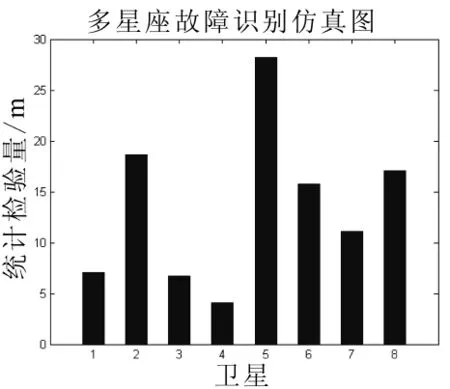
图5 阶跃故障识别仿真图

3.2 多星座RAIM与单星座RAIM比较

为比较多星座RAIM与单星座（GPS系统）RAIM的性能，选取某颗卫星为故障星，在此观测卫星的伪距中加入故障偏差，偏差值从0 m递增到200 m，步长为10 m。再使用奇偶矢量法进行10 000次Monte-Carlo仿真，取误警率为1/150 000。从故障检测率、故障识别率两个方面衡量多星座RAIM的性能，仿真结果如图6和图7所示。

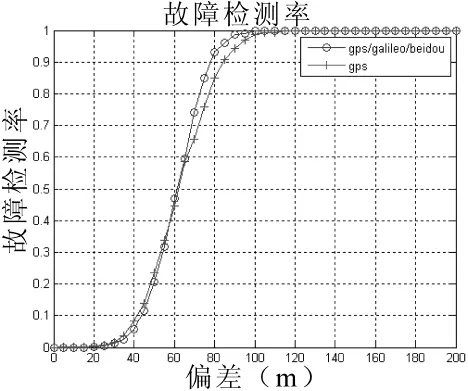
图6 系统故障检测率

图7 系统故障识别率

通过图6对比单GPS系统与多星座系统的故障检测率可以发现，多星座RAIM的故障检测能力要优于单系统RAIM故障检测能力。这体现在当伪距偏差达到100 m时，多星座RAIM能达到100%的故障检测率；而GPS在伪距偏差达到120 m时才能实现几乎100%的故障检测率。多星座系统通过增加可见卫星数目，增加RAIM的冗余信息，可以提高RAIM的可用性，减少RAIM空洞，在一定程度上能够提高RAIM算法性能。

通过对比图7单系统导航与多星座导航RAIM的故障识别率同样可以发现，多星座导航的故障识别能力要优于单系统导航故障识别能力。从仿真图可以看出当伪距偏差达到100 m时多星座RAIM的故障识别率可接近100%，而单星座RAIM即使当伪距偏差达到200 m也只能实现95%的故障识别率。其原因与组合导航的故障检测能力要优于单系统导航故障检测能力的原因相同。

4 结 论

本文利用奇偶矢量算法系统分析了多星座RAIM的故障检测和识别，并比较了单星座和多星座的故障检测率和故障识别率。仿真结果表明，多星座系统下RAIM算法可以提高传统的单星座系统下RAIM算法的故障检测率和故障识别率。

［1］王尔申，张淑芳，胡 青.GNSS接收机自主完好性监测算法研究［J］.通信技术，2010，1（43）：213-214.

［2］秘金钟.GNSS完备性监测理论与应用［M］.北京：测绘出版社，2012：1-2.

［3］Liu R H，Zhan X L.Study of RAIM Algorithm and Availability Analysis Under COMPASS［C］//IEEE 2011：4346-4349.

［4］陈 婷，佀 荣，史彦芳.GNSS接收机自主完好性检测算法研究［J］.电子设计工程，2013，21（2）：97-99.

［5］李 飞，段哲民，龚 诚，等.GPS接收机自主完好性监视算法研究及仿真［J］.测绘科学，2009，34（1）：14-15.

［6］范振新，常 青，刘 莉.适用于多星座接收机的RAIM算法［J］.信息与电子工程，2012，10（3）：252-256.

［7］Lee Y.Analysis of Range and Position Comparison Methods as a Means to Provide GPS Integrity in the User Receiver［C］// ION AM 1986，Seattle，WA，USA，1986.

［8］Parkinson B，Axelrad P.Autonomous GPS Integrity Monitoring Using the Pseudorange Residual［J］.Navigation：Journal of the Institute of Navigation，1988，35（2）：255-274.

［9］Sturza M.Navigation System Integrity Monitoring Using Redundant Measurements［J］.Navigation：Journal of the Institute of Navigation，1988，35（4）：483-501.

［10］蒋 凯.卫星导航系统完好性指标分析与算法研究［D］.长沙：国防科技大学，2011：7-11.

［11］代长勇，常 青，陈 媛.多系统卫星导航接收机自主完好性监测［J］.遥测遥控，2010，31（6）：11-14.

［12］Brown R G.A Baseline GPS RAIM Scheme and a Note on the Equivalence of Three RAIM Methods［J］.Navigation：Journal of the Institute of Navigation，1992，39（3）：301-316.

［13］郭承军.GNSS全球导航卫星系统完备性监测体系研究与设计［D］.成都：电子科技大学，2011：17-19.

［14］Safety Regulation Group.GPS Integrity and Potential Impact on Aviation Safety［R］.CAA THESIS，2003，9.

Research on Multi-constellation RAIM Based on Parity Vector

LI Cha
（School of Electronics and Information Engineering，Northwestern Polytechnical University，Xi'an 710129，China）

With the development of GNSS receiver technology，the GNSS receiver autonomous integrity monitoring（RAIM）algorithm based on multi-constellation also has been widely studied both at home and abroad.The paper firstly introduces the RAIM algorithm under the single-constellation and the combination of multi-constellation respectively，then carries simulations.Graphics and data simulation results testify the performance of integrity monitoring under the combination of multiconstellation is superior to single-constellation.

GNSS，RAIM，Parity vector，Multi-constellation

TP30

A

1002-0640（2014）11-0187-04

2013-08-05

2013-10-20

西北工业大学研究生创业种子基金资助项目（Z2013073）

李 查（1986- ），女，陕西西安人，硕士研究生。研究方向：GNSS接收机自主完好性监测方面的研究。