基于改进MS-EM算法的贝叶斯网络学习法构建基因调控网络①
方跃胜, 姚宏亮
(1.安徽水利水电职业技术学院,安徽合肥 231603;2.合肥工业大学计算机与信息学院,安徽合肥 230009)
0 引言
基因调控网络(GRN,Gene Regulation Network)的研究目的是期望从系统的角度全面揭示基因组的功能和行为.基因调控网络是由细胞中相互作用的基因片段以及其它起调控作用的物质共同构成的调控网络,它表征了细胞中基因之间的调控关系,指导着基因到mRNA的表达过程[1].在基因调控网络的建模方面主要的数学模型和方法有:线性模型、布尔网络模型、聚类分析和贝叶斯网络等[2].以上是系统生物学中常用的建模方法.但由于这些模型对数据和建模对象的要求很高,目前在实际应用中还有许多问题有待解决.生物信息学研究的一个热点是利用贝叶斯网络构建基因调控网络,贝叶斯网络被认为是构建基因调控网络的最有前途的方法[3].
贝叶斯网络亦称信念网络(Belief Network),它是一种不确定性处理模型,用来模拟人类推理过程中因果关系的[4].根据处理的基因表达数据无序与有序的区别,贝叶斯网络分为静态和动态两个分支.学习贝叶斯网就是要寻找一种能按某种测度最好地与给定实例数据集拟合的网络.贝叶斯网络结构学习的关键在于寻找到一个好的搜索算法和一个对网络结构进行有效评估的方法[5].
目前用于贝叶斯构建基因调控网络的贪心搜索GS、MWST和K2等网络学习算法,常被用来处理完备数据下的结构学习.EM(Expectation Maximization)算法通过对数据进行充分统计来得到后验概率分布的平均估计,然后通过最大似然得到和数据拟合的最好的网络.另外,EM算法对用于学习的数据依赖小,数据可以不完备.标准的EM算法是用于丢失数据的参数估计的,它是对固定网络结构进行参数学习.Friedman[6]等人提出了一种扩展的EM算法可以进行结构学习,称为MS-EM算法(Model Selection EM algorithm)[7].
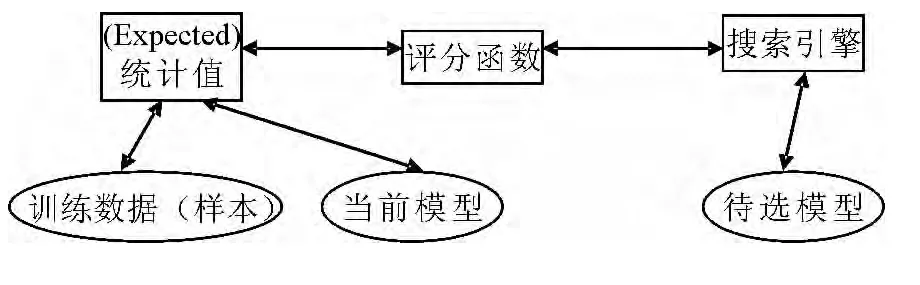
图1 改进的MS-EM算法实现结构
1 改进的MS-EM算法
本文采用改进的MS-EM算法进行结构学习.因为从计算上说,最大化一个固定模型的参数比搜索一个更好的模型代价小的多,这个参数的最大化可以使用参数EM算法得到,参数EM算法运行指定的步数,或者运行到收敛为止,然后才考虑改变模型的选择来获取评分的改进.这种算法在某些情况下还可以避免局部极大化.改进的算法描述如下:
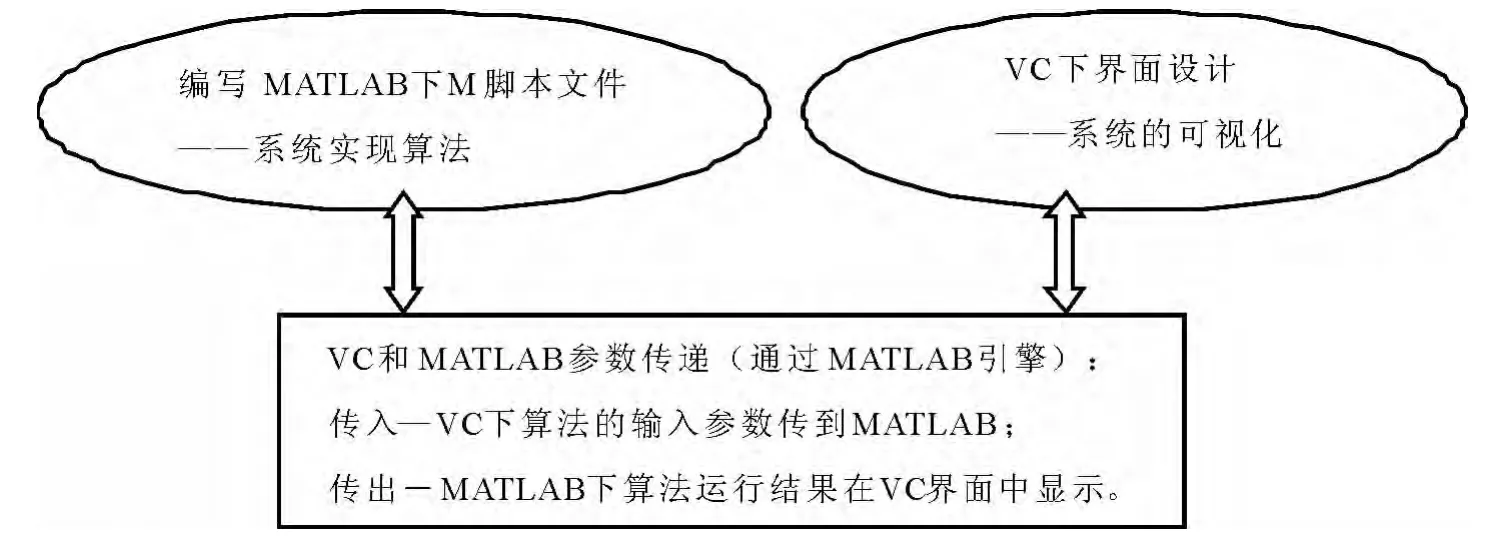
图2 系统开发流程图

图3 实验平台的进入界面
随机的选择 M0和 θ0,loop n=0,1,….直至算法收敛,loop l=0,1,….直至算法收敛或者 l=lmax,使得,寻找一个模型 Mn+1,使得最大化让参数).改进的算法实现结构如图1所示.
搜索引擎模块负责选择等待评价的模型,对于每个待选模型,搜索引擎调用评分函数模块,它执行某种评分函数(例如:MDL或者Bayesian评分函数,本次设计使用MDL评分函数),为了评价得分,评分模块需要调用相应的统计值,统计模块通过计算样本数据的期望来“回答”评分函数.这个算法根据统计模块和推理算法的不同,会有细微的变化.
2 算法的设计与实现
2.1 基因数据来源及预处理
目前研究基因调控网络的主要手段之一,是使用概率图模型中的贝叶斯网络[8].贝叶斯网络具有丰富的随机特性,所以特别适合于处理微阵列数据这样由于实验条件限制而含有大量噪声的数据.本文中使用Spellman[9]等人于1998年提出的啤酒酵母(Saccharomyces Cerevisiae)细胞周期微阵列表达谱数据集.这些基因表达数据集描述了酵母菌在细胞周期过程中的基因表达特性.算法中要求数据是离散的,所以在编写算法中将连续的数据进行了离散化处理.
2.2 系统的总体要求
开发环境:用VC作界面,调用MATLAB下的M脚本文件实现功能.
功能要求:(1)采用EM算法从样本学习贝叶斯网络的结构,输出学习所用时间和得分;(2)实现可视化界面,进行可视化操作,输出最终得到的基因调控网络图.
2.3 系统的实现流程
本系统是在Windows环境下,采用VC6.0作界面,以调用 MATLAB引擎的形式执行 MATLAB7.0下编写的M脚本文件和函数、参数传入和传出,从而把VC的可视化与MATLAB强大的科学计算这两个优点相结合.系统开发流程如图2所示.(至于脚本文件与函数的编写,开发环境设置及VC与MATLAB的参数传递,这里不再赘述.)
根据M脚本文件,设计VC界面,实现MATLAB下的抽象算法的可视化.实验中选取了两组数据分别进行试验,并分别与参考文献中的正确网络图进行比较,以察看算法的正确率.该系统是静态概率模型构建基因调控网络.实验平台的VC界面设计及运行效果如图3所示.
点击“进入”:进入实验平台的MS-EM算法学习界面,如图4、5所示.
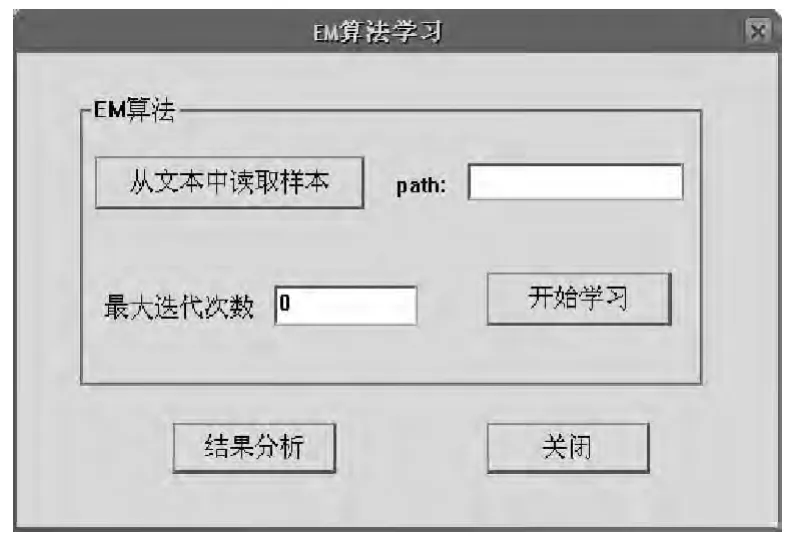
图4 算法学习界面
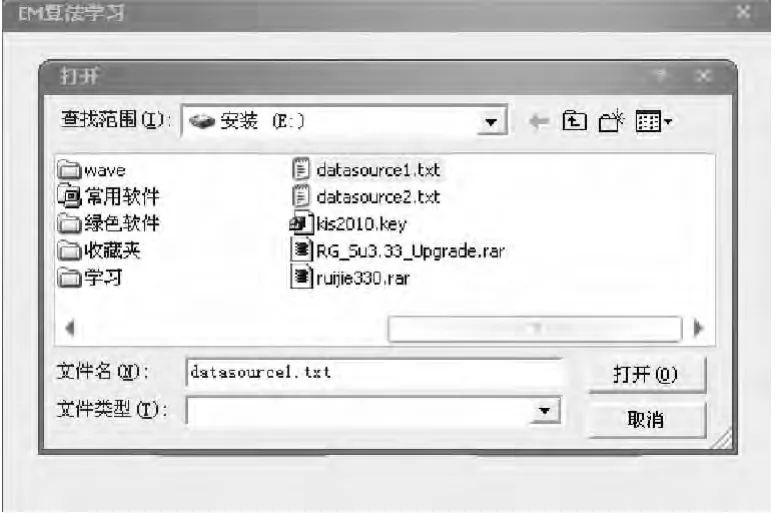
图5 打开文件获取路径名
图6 输入最大迭代次数执行EM算法
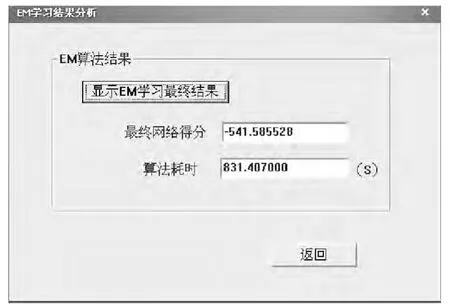
图7 结果分析页面
(1)第一组数据
打开数据组1,构建酵母菌的细胞周期调控网络,使用的数据选择Futcher[10]所列的主要转录因子:MBP1,SWI4,SWI6,FKS1,ACE2,CDC28,CLN3,CLB2,SIC,CLN2,HHT1,MCM1,FKH1,NDD1和SWI5(FKH2除外,因为在所用的数据库中,FKH2基因的缺失值的比例过大).其中MBP1,SWI4和SWI6主要结合在G1晚期基因的启动子,MCM1,FKH2和NDD1结合于G1/M期基因,SWI5和ACE2结合于M/G1期基因,另外FKH1在G1、S和G1/M期都有结合.
下面是EM算法学习运行界面:可输入最大迭代次数,然后开始学习.点击“开始学习”按纽,则调用MATLAB引擎,执行em脚本文件.如图6所示.
算法运行耗时,得分:为了评价重构的网络,并且选择与真实情况最接近的网络结构,需要对网络进行评分.在同样的标准下,得分越高的网络就越接近真实情况.如图7所示.
显示最终网络图:针对基因调控网络建模问题来说,贝叶斯网络的节点表示的是不同的基因,而节点之间的边表示两个基因之间是否有基于概率的调控关系,边的方向表示的是调控方和被调控方.实验中共使用了15个基因作为节点,基因之间调控关系如图8所示.
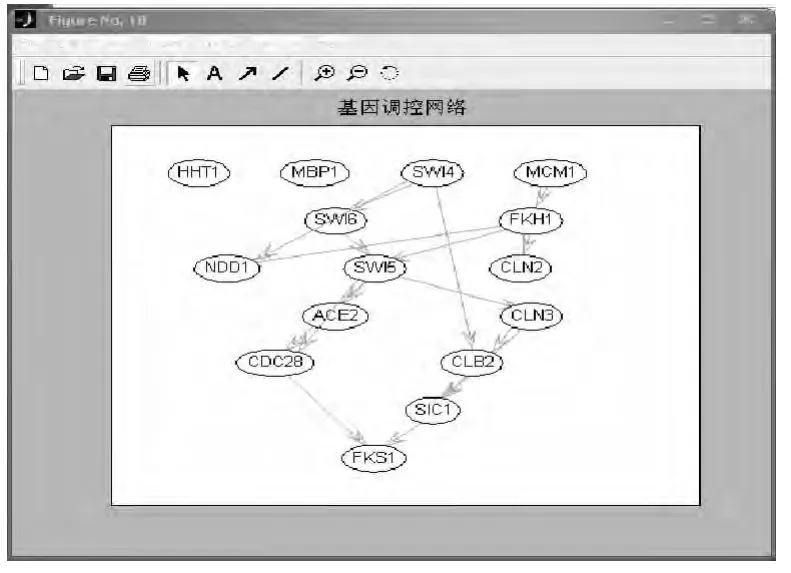
图8 基因调控网络图
(2)第二组数据
数据来源:我们使用的仍然是从先前的对酵母细胞周期的基因调控(Spellman et al.,1998)的研究得到的公开的数据.共18个基因,包括组蛋白基因 HHT1,HHF1,HHF2,HTA1,HTA2,HTB1 和HTB2,还包括在细胞周期中比组蛋白基因执行不同功能(如DNA初始复制,DNA损伤修复等)的基因.这些酵母菌数据从http://genome-www.stanford.edu/cellcycle/data/rawdata/individual.html 下载,并根据 http://www.yeastgenome.org/SGD 数据库将系统名称转为标准名称.
为了进一步评估算法的性能,我们选择第二组数据开始学习,同样迭代30次.如图9、10所示.
算法耗时,得分:
图9 算法执行
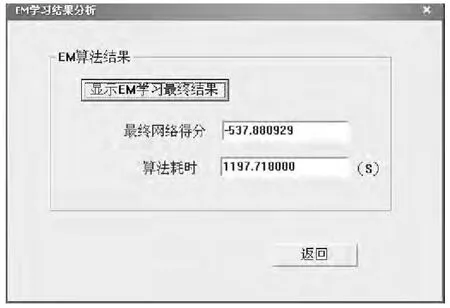
图10 算法结果
最终基因调控网络图:基因之间调控关系如图11所示.
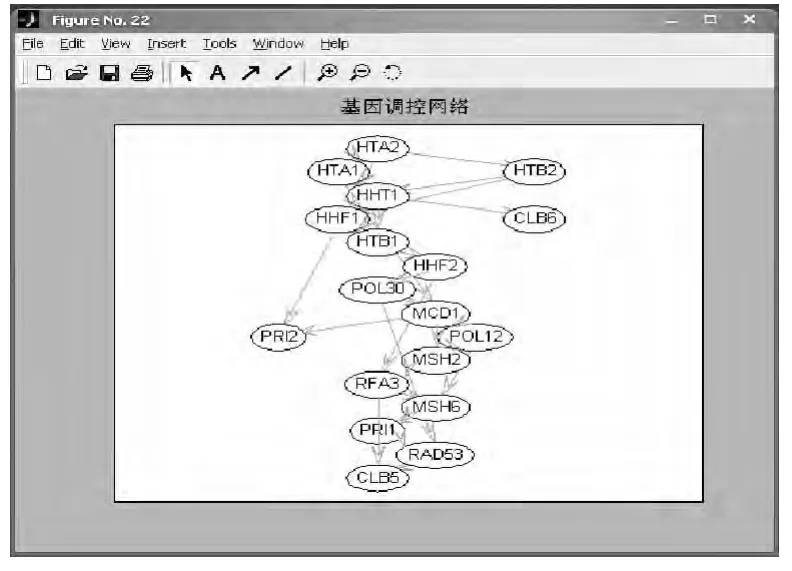
图11 基因调控网络图
3 算法的实验与分析
3.1 结果比较
(1)实验一
参考 Simon I,Barnett J,Hannett N,et a1.Serial regulation of transcriptional regulators in the yeast cell cycle.Cell,2001;106(6):697-708 中正确的调控关系,绘制基因调控网络图.由实验结果绘制的基因调控网络图如图12所示.
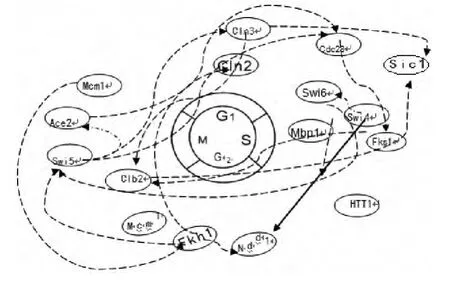
图12 由数据组一得到的基因调控网络
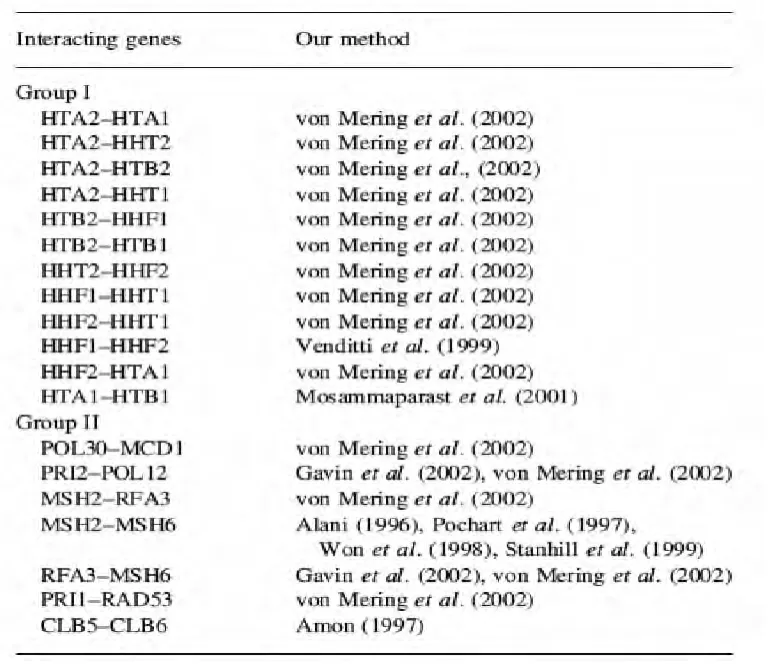
图13 基因调控关系参考图

图14 由数据组二得到的基因调控网络
实线表示已经被验证存在的边结果中有一条,占总边数的6%;点划线表示错误的边(与正确边方向相反的边),由于偶然或数据噪声造成,结果中有两条,占总边数的12%;长划线表示的边为未被现有文献证明的,其中有些可能是正确的.
(2)实验二
正确的基因调控关系参考如图13所示,基因之间的调控关系是通过PathwayAssist软件获得的,作为本次实验的参考.
通过本次实验绘制的基因调控网络图如图14所示:
图中实线表示可由PathwayAssist得出的边,即已被证明是正确的边,共五条,占总边数的19%;点划线表示错误的边,即与已证明的正确边反向的边,占12%;长划线表示为现有文献还不能证明的边.
3.2 结果分析
学习结果中文献尚未证明的边较多,正确的边相对较少,分析其原因,一是现有技术正确率都不太高,且尚未被文献证明的边有可能是正确的,因为目前关于基因调控关系的已有知识还是比较匮乏的.贝叶斯网络方法不仅可以构建已经存在的基因关系,而且可以发现一些基因间的新关系.二是所使用的基因数据有限.若要使得学习结果与真实网络更加拟和,可提高所使用样本的数量,样本数量越多,学习结果就与真实越趋近.
4 结束语
本文借助于VC6.0和MATLAB7.0通过分析、设计、到编程完整实现了基因调控网络EM算法的学习,并设计了友好的用户使用界面,用于显示每一步的结果并与正确结果进行比较.实验结果表明改进后的算法进一步降低了时间性能,提高了构建调控网络的精度.但仍存在不足之处,需进一步改进EM算法,这也是今后应该解决的问题.另外,考虑到EM算法耗时太长,本文只是在一个很小规模的模型(15个节点)上进行了试验,今后应该在该改进MS-EM算法的时间性能的基础上,对大规模的网络进行学习,从而把EM算法应用于实际生活当中.
[1]DE Jong H.Modeling and Simulation of Genetic Regulation System:a Literature Review[J].Journal of Computational Biology,2002,9(1):67-103.
[2]Friedman N,Linial M,Nachman I,et a1.Using Bayesian Network to Analyze Expression Data[J].Journal of Computational Biology,2000,7(1):6O1-62O.
[3]Heckerman D,Geiger D,Chickering D M.Learning Bayesian Networks:the Combination of Knowledge and Statistical Data[J].Machine Learning,1995,20:197- 243.
[4]D.Heckerman,Atutorialon Learning with Bayesian Networks[J].Microsoft Research Tech Report,MSR- TR- 95- 06.1996,300-302.
[5]强波,王正志.基于动态贝叶斯网构建基因调控网络[J].生物医学工程研究,2008,27(3):145-149.
[6]Nir Friedman,“Learing Belief Networks in the Presence of Missing Values Hidden Variables”[J].Computer Science Division U-niversity of alifornia,Berkeley CA94720,1998:139-147.
[7]Liu.C and Rubin,D.B(1994).The ECME Algorithm:A Simple Extension of MS-EM and ECM with Faster Monotone Convergence[J].Biometrika 81.
[8]Lauritzen S L.The EM Algorithm for Graphical Association Models with Missing Data[J].Comput.Stat Data Anal,1995,(19):191-201.
[9]Spellman P T,Sherlock G,Zhang M Q,et a1.Comprehensive Dentification of Cell Cycle-Regulated Genes of the Yeast Saccharo Myce Scerevisiae by Microarray Hybridization[J].Molecular Biology of the Cell,1998,9:3273-3297.
[10]Futcher B.Transcripti0nal Regulation Networks and Yeast Cell Cycle[J].Current Opinion in Cell Biology,2002,14:676-683.

