基于灰度共生矩阵的板材纹理模糊分类器设计1)

张怡卓 许 超 李 想 薛 瑞

(东北林业大学，哈尔滨，150040)

木材生长条件与加工方法将使其产生不同形状的纹理，不同的纹理会直接影响到木制品的视觉和触觉美感。因此，对板材纹理进行合理地分类对提升木产品质量具有积极的现实意义。数字图像分析中的空间灰度共生矩阵法在实际应用中已经日趋成熟，并且对木材纹理描述效果的有效性已经得到了验证。王克奇运用灰度共生矩阵与神经网络结合对木材表面纹理进行了研究［1］。白雪冰提出了一种基于灰度共生矩阵与模糊C均值聚类算法的纹理分割方法［2］。王克奇应用灰度共生矩阵提取出了一套表征木材纹理的特征参数［3］。木材纹理与人们的感觉有着很大的相关性，对于木材纹理的描述夹杂着语言语义的特点，对不同纹理的语言定义、客观描述不是十分确定，语句中存在模糊性。因此，运用模糊分类对纹理进行分类具有适用性。尽管灰度共生矩阵可以描述纹理，但是灰度共生矩阵方法参数较多，构建模糊分类器复杂，笔者将研究优选灰度共生矩阵的纹理特征量，并在此基础上构建纹理特征的模糊分类器，实现纹理的直纹与曲纹的有效分类。

1 灰度共生矩阵及纹理特征选择

1.1 灰度共生矩阵

空间灰度共生矩阵通过计算统计灰度图像中一定距离和一定方向的两像素点灰度之间的相关性得到它的共生矩阵，然后对这个共生矩阵进行计算，得到这个矩阵的二次统计量，用来代表图像的某些纹理特征。

常用的纹理特征量有11个，分别是角二阶矩、对比度、相关性、方差、逆差矩、均值和、方差和、和熵、熵、差的方差、差熵等，但是并非所有的特征量都适用于纹理检测，因此对灰度直方图进行二次统计量的计算，得到 14个二次统计量［3－5］。在这 11个纹理特征量和14个二次统计量中，能量、相关性、一致性、逆差矩这4个特征已被证明线性不相关［6］;而且在建立模糊分类器时，二维纹理特征的模糊分类器结构清晰，运算分类速度快，能使分类器性能达到最优。因此，优选特征量是合理构建模糊分类器的关键。

1.2 基于灰度共生矩阵的纹理特征选择

使用穷举法对能量、相关性、一致性、逆差矩这4个特征量两两组合，综合比较每一组特征参量对于分类效果的表现。把4个特征量分为6组，分别是一致性—相关性、一致性—能量、一致性—逆差矩、相关性—能量、相关性—逆差矩、能量—逆差矩。选择200幅直纹和200幅非直纹的木材图片作为试验样本，经组合得到6组特征量的变化及分布情况(见图 1、图 2)。

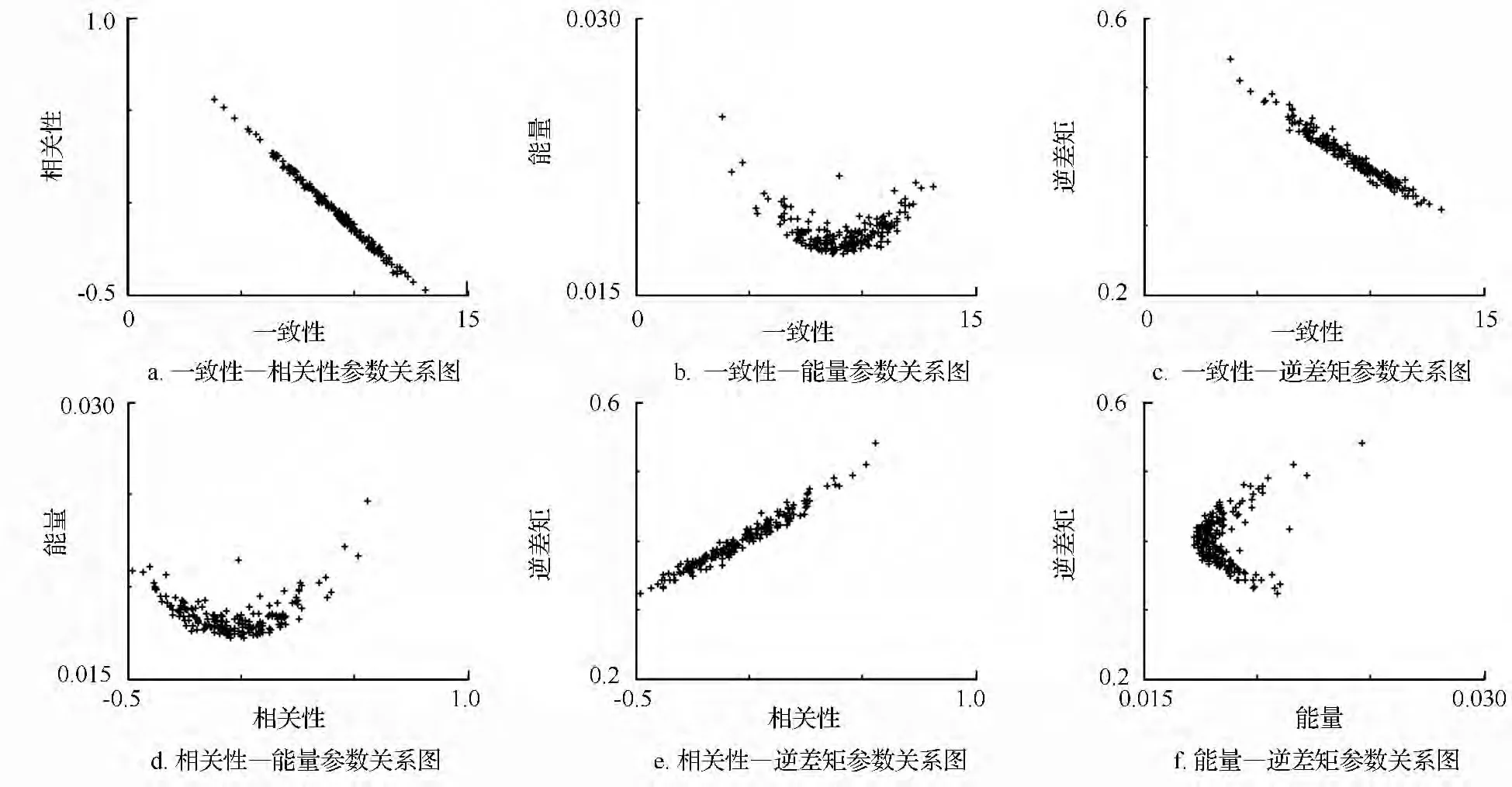
图1 直纹的各个特征组合

图2 非直纹的各个特征组合

一致性—相关性、一致性—逆差矩、相关性—逆差矩3个子图的分布线近似直线，表明一致性、相关性、逆差矩特征量的线性相关性较强，因此，在这3个特征量中选择一个特征作为模糊分类器的变量即可。把3组直纹样本的值归一化后求方差，发现相关性的方差最小，说明聚类效果最好，因而选定相关性为输入变量。最终模糊分类器的两个输入变量选择相关性—能量。

2 基于模糊分类器的纹理辨识

2.1 模糊分类器的设计流程

设计模糊分类时首先要先确定分类器的结构;然后，将输入量进行模糊化处理，它可以分为两个主要部分，一是精确量的离散化，二是离散量的模糊化;输入量模糊化处理之后就要对输出变量进行清晰化处理。应用模糊逻辑进行纹理分类时，输出变量表示图片纹理属于直纹的程度。在定义输入量和输出量基础上，提取模糊分类器的模糊规则，进而离线生成纹理模糊分类查询表。

2.2 模糊分类器的解模糊方法

由于纹理模糊分类器为二维，结构较清晰明了，在此采用Mamdani－MIN－MAX－重心法来解模糊［7］。由前提“x0andy0”和各模糊规则“AiandBi→Ci(i=1，2，…，n)”可以得到推理结果 Ci。

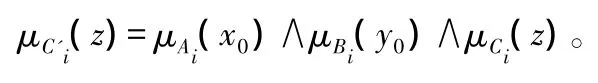
其中∧表示最小。上式的最终结论C＇是由综合推理结果 C＇1，C＇2，C＇3，…，C＇n得到的，即

其中∨表示最大。

模糊集合C＇的重心可由下式计算:

3 模糊分类器的设计

3.1 样本图片的预处理

选用100个柞木锯材作为分类器设计样本。由于摄像视野不同，导致木材纹理在同一张图片中的多样化，截取5～9个直条纹，或者近似大小的弯条纹作为待处理的样本图片，并整理归类(见图3)。

图3 木材纹理样本图片的采集

3.2 输入变量的模糊化

图4为能量—相关性分布变化范围，选定两者的基本论域分别为(0.016，0.029)、(－0.6，0.6)，确定论域为(－8，8)、(－10，10);然后将能量基本论域划分成(0.016，0.017］、(0.017，0.021］、(0.021，0.026］、(0.026，0.029)4 个区间并映射到论域的(－8，－7］、(－7，1］、(1，6］、(6，8)4 个区间。相关性的基本论域划分为(－0.6，－0.2］、(－0.2，0.4］、(0.4，0.8)3 个区间并分别映射到论域(－10，－6］、(－6，6］、(6，10)中。

选择描述能量的状态词汇为{NB、NM、NS、NZ、Z、PZ、PS、PM、PB}，相关性的状态词汇为{N、NB、NM、NS、NZ、Z、PZ、PS、PM、PB、P}。选择三角型、Z型、S型3种隶属度函数完成变量的模糊化。

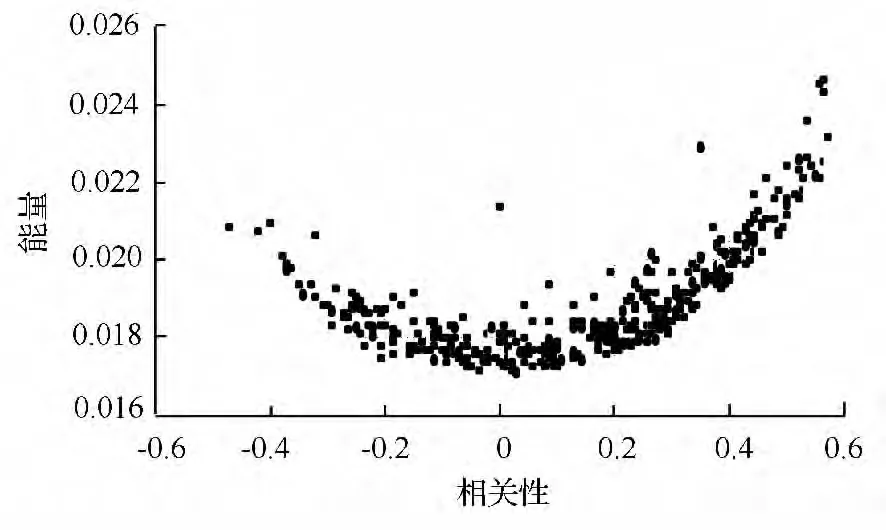
图4 能量—相关性分布

图5 隶属函数类型

3.3 输出变量的清晰化

输出变量表示该幅图片的纹理属于直纹的程度，值域在［0，1］，取值越大表示越接近直纹。约定输出变量的精确值大于0.5时，判断当前图片为水平方向直纹;等于0.5时，不进行判断决策;小于0.5时，认为当前图片为弯曲纹理。

3.4 模糊规则的提取

模糊分类器的分类规则是设计模糊分类器的关键，每条分类规则的确定都会在一定程度上影响分类器的性能。图4中，每一个虚线框都代表了一个规则，每个虚线框所在的位置是规则的前提，虚线框内所包含的点的比例是规则的结论。针对二维模糊分类器，选用“若A且B则C”条件语句来表述语言变量，生成了30条模糊分类规则。经整理，得到表1的模糊分类规则。

3.5 模糊推理及查询表

在模糊分类器进行工作时，对建立的模糊规则要经过模糊推理才能决策出输出模糊变量的一个模糊子集。因此，当历遍所有的输入模糊变量的论域后，结合对输出模糊变量的清晰化计算，得到空间查询表。本研究所设计的模糊分类器采用Mamdani－MIN－MAX－重心法，并使用Matlab软件实现。

表1 模糊分类规则控制表

图6 模糊推理仿真

3.6 分类结果

为了验证模糊分类器的性能，在样本的灰度图片库中随机抽取直纹和弯纹各100幅样本进行验证，检验结果见表2。

表2 模糊分类器仿真结果数据

4 结论

针对板材表面的直纹与弯纹两类纹理，提取了灰度共生矩阵的能量与相关性两类特征量，并应用模糊逻辑设计了基于两类特征的纹理类型分类器。对样本的实验分析表明，基于灰度共生矩阵的能量与相关性的模糊分类器具有较好的纹理分类能力。

［1］白雪冰，王克奇，王辉.基于灰度共生矩阵的纹理分类方法的研究［J］.哈尔滨工业大学学报，2005，37(12):1667－1670.

［2］白雪冰，王科俊，邹丽晖.基于灰度共生矩阵的木材表面缺陷图像的纹理分割方法［J］.东北林业大学学报，2008，36(12):23－25，27.

［3］王克奇，陈立君，王辉，等.基于空间灰度共生矩阵的木材纹理特征提取［J］.森林工程，2006，22(1):24－26.

［4］王亚超，薛河儒，多化琼.基于9/7小波变换的木材纹理频域特征研究［J］.西北林学院学报，2012，27(1):225－228.

［5］王克奇，杨少春，戴天虹，等.基于均匀颜色空间的木材分类研究［J］.计算机工程与设计，2008，29(7):1780－1784.

［6］黄桂兰，郑肇葆.空间灰度相关在影像纹理分类中的应用及分析［J］.武汉测绘科技大学学报，1995，20(4):301－304.

［7］李士勇.模糊控制·神经控制和智能控制论［M］.哈尔滨:哈尔滨工业大学出版社，2006:24，256－257，263－280.