移动单站定位的线路规划技术研究

徐铂韬，张 毅，刘亚欧

(中国电子科技集团公司第五十四研究所，河北石家庄050081)

0 引言

移动测向站以其系统简单、成本低、机动性和灵活性强、技术成熟和平台适用性广等特点，越来越广泛的应用于各个领域［1］。移动测向站在使用过程中，用户往往更加关心对目标的定位效果，也就是定位精度。影响定位精度的因素有很多，除了测向系统客观存在的测向误差外，测向站距离目标的距离、测向数据质量和数据量等因素都会对定位精度产生很大的影响［2－4］。针对移动测向站观测点的选取对交会定位精度的影响程度做了重点分析和说明，据此提出了移动测向站路线规划原则。移动测向站可以是地面车载测向系统，也可以是机载测向系统，本文以机载无源测向系统为平台，对静止目标采用交会定位的方法进行仿真分析和实验。

1 交汇定位与误差

移动测向站交汇定位是利用不断变换测向站所在的位置，对同一固定辐射源目标进行多次多点的测向，然后通过几何交会的方法确定辐射源的位置［5，6］。在没有误差的理想情况下，所有的测向点所获取的示向线会交叉于同一个点，即目标辐射源的位置。但是实际情况下，由于误差的存在，多条示向线并不能交会在同一点，而是分布在一定大小的区域中［7－9］，如图1 所示。

图1 交汇定位

由图1可见，在实际情况下示向线交会定位所获得区域与最终的定位精度存在着密切关系，在有效测向数据量足够大时，交会定位区域越小，则获得的目标位置越真实，定位精度越高［10－12］。由此可见，如果要提高目标定位精度，需要从测向数据的质量和数量上着手。在不改变测向系统的测向精度的条件下，可以通过合理规划移动测向站的工作路线，在较短时间内获取高质量的有效测向数据，从而提高目标定位精度。观测点与交汇区域的关系如图2所示。

图2 交汇定位

在图2中，目标辐射源位于E(x，y)点，测向站分别在A(x1，y1)点和B(x2，y2)点进行了2次测向，方位角分别为θ1和θ2，交会角为β，AB两点距离为L，假设测向系统的测向误差为Δθ1和Δθ2服从均值为0、方差为的高斯分布。由于测向误差的存在，这2次测向的示向线交会于E点周围由虚线所围成的四边形区域的某个点，因此这个区域越小，目标的定位误差越小。需要注意的是，当出现θ1=θ2或θ1=θ2+π 的情况时，说明A和B两个测向点与目标E点在同一直线上，这样是不能确定目标位置的，这种情况本文暂不做讨论。

2 交会角与最小圆概率误差分析

由图2 可见，交会角为β =θ2－ θ1，由A(x1，y1)、B(x2，y2)两点坐标和和角度θ1和θ2不难求出目标辐射源E(x，y)位置为:

由设置的坐标系可知x2－x1=L、y2=y1，并且目标到AB点连线的距离:

对式(1)和式(2)通过运算可获得的目标x、y轴的定位误差和协方差，再将式(3)带入，可求出圆概率误差:

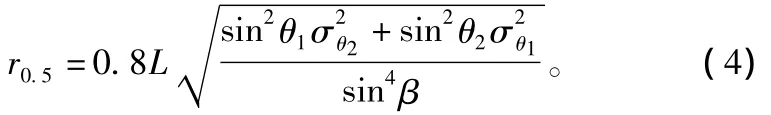
式中，σθ1和 σθ2的单位为弧度。

由式(4)可见，圆概率误差r0.5是由AB点距离L、测向误差的方差为、以及方位角 θ1和 θ2等因素决定的。对于某一测向系统来说测向误差的方差可设为，并令

如要使圆概率误差r0.5达到最小，则对上式θ1、θ2求导，并令其导数为0，可得

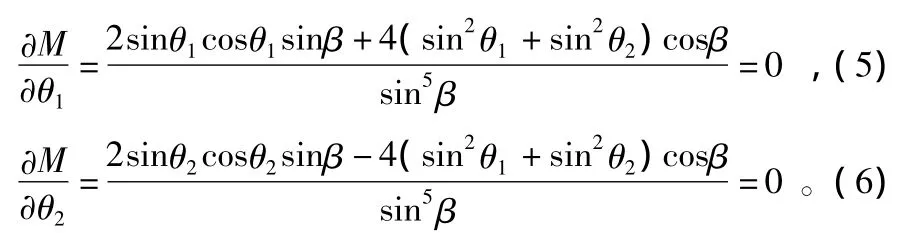
由于 θ1≠θ2，即 sinβ =sin(θ2－ θ1)≠0，带入式(5)和式(6)，整理后得

因目标点E与测向点A、B不在同一条直线上，那么由式(7)可得 θ2= ±π －θ1，带入到式(5)和式(6)中，可解得，那么可得当时圆概率误差r0.5达到最小，此时交会角，测向点A、B与目标距离相同，且AB之间的距离L为A点(或B点)到目标距离的1.414倍。圆概率误差r0.5与交会角β的关系如图3所示。

图3 圆概率误差与交会角的关系

通过以上分析可知，移动测向站在对同一固定目标多次测向和定位时，为了在最短时间内获得最佳的定位数据，测向点应尽量满足以下条件:

①2次测向的位置和目标位置距离相同;

②2次测向位置之间的距离为到目标距离的1.414倍。

理论上，在对移动测向站进行线路规划时，应以尽量满足以上2个条件为原则。但是实际工作中，往往不知道目标点E的确切位置，因此很难据此确定出最佳的移动路线。在利用移动测向站定位的实际使用过程中，一般能够划定出某个的关注区域，根据关注区域的形状制定出粗略的移动测向路线，再根据不断获得的测向定位结果对路线进行修正。当所关注的区域较为窄而深时，最初路线可设定为正C型路线，当所关注的区域宽而浅时，最初路线可设定为L型路线，如图4所示。

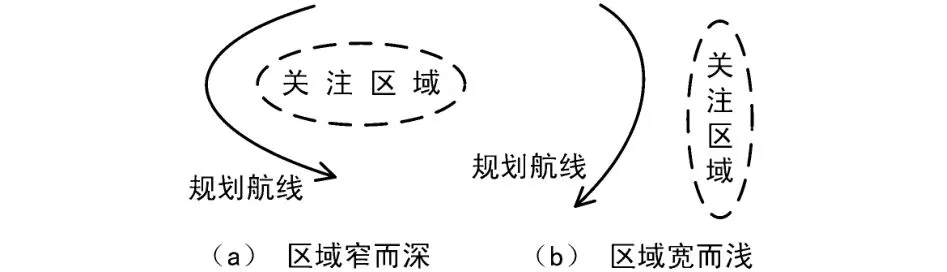
图4 关注区域与最初路线设定

如果无法划定关注区域的范围，或者关注区域范围过大，可采取圆形路线作为初始路线，并且圆形路线的半径设定要相对足够大。根据初始路线工作一段时间，在获取了一些测向定位信息后，再根据最佳路线规划原则，实时调整工作路线。工作流程如图5所示。

图5 实际工作流程

3 结束语

结合实际提出了一些新的观点和方法，研究了移动测向站交会定位数据模型，推导出精度达到最高时的测向位置，并依此为原则规划和修正移动测向站的工作路线，解决了移动测向站在实际使用过程中的一些技术难题。该问题的研究使移动测向定位系统在规划工作线路问题上有了一定原则，为提高测向站对目标定位精度有着重要工程使用价值，可推广到相关使用过程中。

［1］翟庆伟.机载单站无源定位技术研究［J］.无线电工程，2007，37(3):50 －52.

［2］邱丙益，盛 莹，刘春茂.基于TDOA的短基线测向精度分析与仿真［J］.无线电通信技术，2013，39(1):67 －69.

［3］孙 玮，刘国满.基于DSP的脉冲压缩算法的并行流水实现［J］.无线电工程，2013，43(9):48 －50.

［4］孙 彪.基于单目视觉的运动目标跟踪定位［J］.四川兵工学报，2010，31(4):85 －86.

［5］柴立功，樊甫华，董世友.无人机群通用控制站的技术需求分析［J］.无线电工程，2013，43(10):1 －3.

［6］钱志柏，陈 娜.基于DSP的相关干涉仪测向快速实现方法［J］.无线电工程，2011，41(8):47 －50.

［7］卢发兴，高 波，邢昌风，王国根.测量站数量对多站测向交叉定位精度的影响［J］.火力与指挥控制，2011，36(2):50 －52.

［8］汪 珺.测向交叉定位技术［J］.电子科技，2011，24(7):129－131.

［9］廖 平，付 忠，刘 刚.采样率波算法在单站无源定位中的应用［J］.电讯技术.2006(4):28－31.

［10］单月晖.空中观测平台对海面慢速运动目标单站无源定位跟踪及其关键技术研究［D］.长沙:国防科学技术大学研究生院，工学博士学位论文，2002:1－16.