Copula EDA与BP结合优化神经网络
刘 洁,王丽芳
(太原科技大学复杂系统与计算智能实验室,太原 030024)
人工神经网络拥有特别的结构和较强的处理信息的能力,近年来,在科技、工业等领域得到了广泛应用。人工神经网络是由大量的神经元通过权值阈值连接而成,分为输入层、隐层和输出层,神经网络的权值训练其实质是一种复杂的连续多参数优化求解的问题,即寻找出一组最优的连接权值。BP网络是一种多层前馈神经网络,其中权值的学习规则是反向传播学习算法,但是由于BP算法是用了梯度下降学习,所以其存在极易陷入局部最小值,收敛速度慢等缺点[1]。有专家在BP算法基础上引入了新参数,虽然在收敛速率和误差估计方面有比较好的效果,但这种方法也有其局限性[2]。粒子群优化是群体智能进化技术,优化神经网络各层之间的连接权值,用实数求解的方法,而且需要调整的参数比较小,这样可以使神经网络有较高的精度。可是由于粒子向的自身、邻域、群体历史最佳位置聚集,容易形成种群的趋同效应,所以不可避免的出现陷入局部极值、早熟收敛或停滞现象[3]。文献[4]用了遗传算法优化神经网络的权值和阈值,遗传算法优化权值阈值的步骤分为:选择、交叉、变异三个操作来寻求最优解,虽然其全局搜索能力较强,有效的避免了BP算法容易陷入局部最小的问题,但是交叉、变异过程相对不容易操作,建筑块容易破坏。分布估计算法[5-6]也是基于群体的算法,可以很好的避免遗传算法建筑块被破坏的问题。分布估计算法是从目前的种群中根据一定的选择方式找出一群优秀的个体,然后再得出一个可以描述解的分布的概率模型,通过概率模型随机采样得到新种群,如此反复进行,从而使种群进化,直到终止条件。分布估计算法用于优化神经网络,可在全局范围内、较短的时间内寻求权值阈值的最优解,提高了网络的学习性能,这样就为人工神经网络提供了一种新的优化方法[7]。
1 copula分布估计算法
1.1 copula 理论简介
在copula理论中,Sklar定理[8]起着重要的关键性的作用。
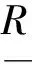
通过该定理可得出:一个联合分布函数在连续时可以唯一的由一个copula函数和各变量边缘分布函数构成;并且对于copula函数及边缘分布函数所确定的联合分布函数同样是唯一的。
1.2 copula 分布估计算法
由于建立分布估计算法的概率模型相对困难,将copula理论引入分布估计算法中可以使其计算简化,运算速度更快[9]。
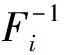
1.3 Clayton copula分布估计算法
1.3.1 Clayton copula分布估计算法简介
Clayton copula分布估计算法[11]是以Clayton copula作为连接函数,以此来描述个体间的联系,该函数的特点是:结构简单、采样方便等,这些特点使得算法更为简单。
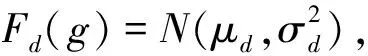
1.3.2 Clayton copula 分布估计算法的步骤
Step1:随机产生规模为popsize的初始群体Pg;
Step2:根据一定的选择策略从当前群体Pg中选择出规模为S的优势群体Sg;
Step3:根据Sg每一维变量的边缘分布。边缘分布采用高斯分布,其分布函数是:
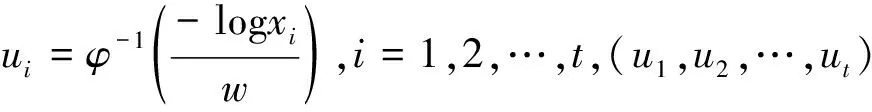
Step5:返回步骤2,如此反复迭代,直到满足迭代终止条件。
2 copula分布估计算法与BP算法结合优化神经网络的权值和阈值
2.1 隐层神经元的确定
神经网络的输入层和输出层神经元个数都由实际问题决定,神经网络的结构是由隐层神经元的个数决定的。在输入层和输出层神经元个数都确定的情况下,确定隐层神经元的个数,目前并没有有效的、合理的办法,一般采用试探的方法,根据学者总结的一些经验公式,如:
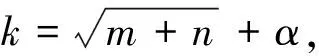
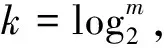

先设置较少的隐层节点数,然后逐渐增加节点数,并用统一样本集训练,当网络的误差函数最小时,就是所要的隐含层神经元的个数。
2.2 神经网络的权值阈值的编码及描述
将神经网络的权值和阈值编码成一个字符串,假设神经网络输入层有m个神经元,隐层有k个神经元,输出层有n个神经元,这个网络的编码码串长度为k(m+n)+k+n,前面k(m+n)表示连接权值个数,k×m表示隐层和输入层之间的权值个数,k×n表示隐层和输出层之间的权值个数。k表示隐层阈值个数,n表示输出层阈值个数。
2.3 选择算子
选择算子[1]的作用是从适应值中选取优秀的个体,通过选择操作可以引导算法向着收敛的方向前进。首先运用截断选择,保留一部分优秀的r个个体,可以把适应值最好的个体保留下来,防止种群的最优个体消失,有利于提高算法的收敛速度,避免有效基因的损失;然后采用轮盘赌选择法选择t个优秀个体,轮盘赌选择对于适应值小的个体也可能选中,可以保证种群的多样性。两者结合起来就是我们得到的S(S=r+t)个优秀个体。
2.4 copula分布估计算法与BP算法的结合
BP网络是利用非线性可微分函数进行权值训练的多层网络,其基本原理是采用梯度最速下降法,它的中心思想是通过各层连接权值的调整使网络总误差最小。BP学习算法包含正向传播和反向传播两个阶段:正向传播是指输入信息从输入层经隐含层逐层处理,并传向输出层,每层神经元的状态只影响下一层神经元的状态;反向传播是将误差信号沿原来的连接通道返回,通过修改各层神经元的权值,使误差信号最小。
copula分布估计算法是一种全局优化搜索算法,能够避开局部极小点,BP算法采用梯度下降学习算法,擅长局部求精。
本文通过神经网络对数据集进行分类,采用copula分布估计算法和BP算法相结合的两种模式优化神经网络的权值和阈值。
模式Ⅰ:首先由初始群体计算适应值函数,得到优秀的S个个体,将优秀的个体通过copula分布估计算法进行优化。copula函数采取Clayton copula函数,边缘分布采用高斯分布,采样得到新的个体,用新个体代替旧个体得到新的种群进入下一代循环迭代,直到达到规定的循环代数,输出经过copula分布估计算法优化的权值和阈值。将经过copula分布估计算法优化得到的最优的权值和阈值作为BP算法的初始权值和阈值,利用BP算法局部求精的特点,做进一步的修正优化,得到最终的权值和阈值。
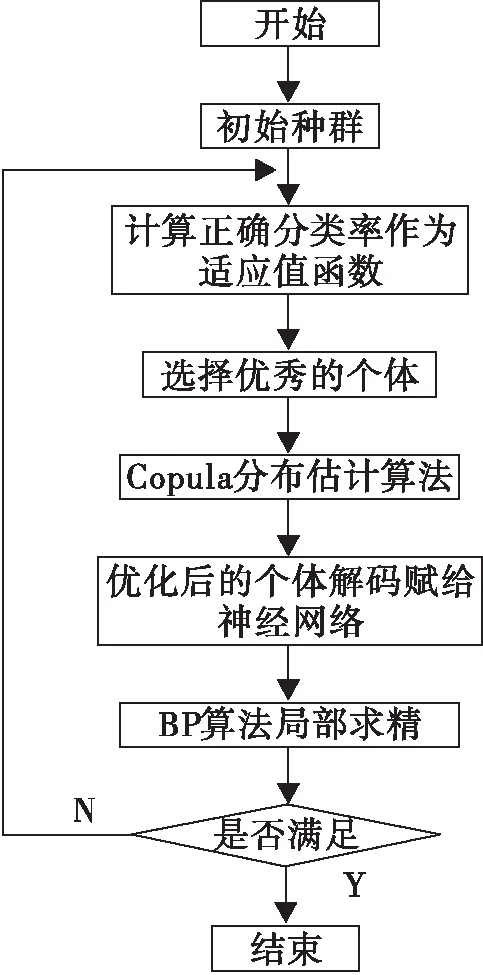
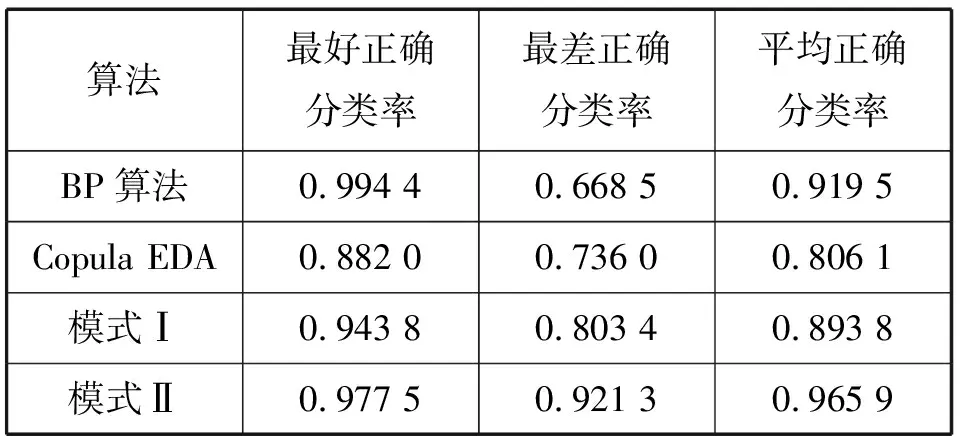
模式Ⅱ:在每次循环的过程中,将copula分布估计算法与BP算法结合起来,首先将选择的S个优秀个体经过copula分布估计算法优化得到新的个体,在新个体中选出优秀的K(K 具体步骤如下: 模式Ⅰ: Step1:首先随机产生popsize组均匀分布的字符串作为初始种群,按照编码方式排列作为神经网络的初始权值和阈值,经过神经网络计算得出popsize个权值阈值对应产生的正确分类率,正确分类率越大,说明对应的权值阈值越好。 Step2:将正确分类率作为copula分布估计算法的适应值函数,按从大到小的顺序排列,采用截断选择选出r个优秀个体和轮盘赌选择算子选择出t个优秀个体,得出正确分类率对应的权值和阈值,作为copula分布估计算法的S(S=r+t)个优秀个体。 Step3:将S个优秀个体通过copula分布估计算法进行优化,copula函数采取Clayton copula函数,边缘分布采用高斯分布,经过copula采样得到R个新个体。将R个新个体,S个优秀个体和随机产生的popsize-R-S个个体作为新的种群进入下一代的循环优化,直到达到收敛条件或迭代次数,选出最好的正确分类率以及其对应的字符串,经解码得到对应的权值和阈值。 Step4:为了进一步提高神经网络的精确性,以及提高网络的搜索效率,当copula分布估计算法运行结束后,我们将得到的最优秀的个体解码后的权值和阈值赋给神经网络,用BP算法进行进一步的修正优化,计算得到正确分类率以及其对应的权值和阈值。 模式Ⅱ: Step1:与模式Ⅰ的第一步相同。 图1 模式Ⅰ流程图Fig.1 Flow chart of model Ⅰ Step2:与模式Ⅰ的第二步相同。 Step3:将S个优秀个体通过copula分布估计算法进行优化,copula函数采取Clayton copula函数,边缘分布采用高斯分布,经过copula采样得到新的个体。在新个体中选出K(K Step4:将优秀的权值阈值进行编码,将K个修正后的优秀个体,S个经copula分布估计算法优化的新个体,截断选择选择出的r个优秀个体和随机产生的popsize-K-S-r个个体作为下一次循环的初始群体,如此反复进行,直到满足收敛条件或达到迭代次数。 Step5:选择最优秀的个体,解码得到权值和阈值,得到最好的正确分类率以及其对应的权值和阈值。 本文用于实验的数据库采用UCI(University of California in Irvine)数据库中模式分类问题数据集:Iris数据库和Wine数据库。 图2 模式Ⅱ流程图Fig.2.Flow chart of model Ⅱ Iris数据库是Fisher教授提出的著名的花朵识别数据库,其以鸢尾花的特征作为数据来源,数据库包含150个数据集,分为3类,三类分别为:Setosa,Versicolour,Virginica,每类50个数据,每个数据包含4个独立属性,这些属性变量测量植物的花朵,有花萼的长度(Sepal length)和宽度(Sepal width),花瓣的长度(Petal length)和宽度(Petal width)。 将Sepal length,Sepal width,Petal length,Petal width作为神经网络的输入,将Setosa,Versicolour,Virginica作为神经网络的输出,因为Iris问题是模式分类问题,所以设定当输出结果为Setosa时,输出为100;当输出为Versicolour时,输出为010;当输出为Virginica时,输出为001. Wine数据库是葡萄酒的识别数据的数据库。这些数据生长在意大利的同一个地区,但来自三个不同品种的葡萄酒的化学分析结果,分析确定13种成分的数量在每个葡萄酒的三种类型。该数据库包含178个数据集,所有的属性都是连续的,13种成分(Alcohol;Malic acid;Ash;Alcalinity of ash;Magnesium;Total phenols;Flavanoids;Nonflavanoid phenols;Proanthocyanins;Color intensity;Hue;0D280/0D315 of diluted wines;Proline)作为神经网络的输入,神经网络的输出分为三类,第一类包括59个数据集,第二类包括71个数据集,第三类包括48个数据集,对于输出分类,通过100,010,001分类。 ①初始化:输入种群规模(popsize),随机产生初始种群{x1,x2,…,xp},p是神经网络的权值和阈值的个数,将权值阈值按照编码法案编码为字符串。在算法的仿真中,种群规模popsize=100. ②计算适应值函数:Iirs数据库的数据集在仿真中可以直接进行运算,而Wine数据库中的数据首先要进行归一化处理。对于分类问题,根据神经网络的测试输出结果与目标输出结果相比较,判断分类是否正确,得出正确分类率,将正确分类率作为适应值函数,正确分类率越大,说明对应的权值和阈值越好。 ③选择优秀个体S=50:首先通过截断选择选择出r个优秀个体,将适应值好的一些个体保留下来,然后通过轮盘赌选择选择t个优秀个体,把两者结合起来共得到S个优秀个体。 ④优化过程:我们通过copula分布估计算法,copula分布估计算法和BP算法结合的两种模式优化神经网络的权值阈值与BP算法修正神经网络的权值阈值进行比较。 本实验通过四种方法优化神经网络的权值和阈值,对四种方法进行比较,实验结果如表1表2所示。 表1 Iris数据库四种方式优化结果比较Tab.1 The result comparisons of four ways ofoptimization on Iris database 从表1、表2中可以看出,虽然copula分布估计算法在复杂度上要高于BP算法, 但是通过比较明显可以看出,第一,copula分步估计算法和BP算法与模式Ⅰ和模式Ⅱ相比较,从最好正确分类率和最差分类率来看,copula分布估计算法和BP算法不如两种模式稳定。从平均正确分类率来看,copula分布估计算法低于模式Ⅰ、模式Ⅱ,虽然BP算法在Wine数据库中的结果最好正确分类率非常高,但是其最差正确分类率也是最低的,说明了它的不稳定性,而且根据多次运行结果显示平均正确分类率也不如模式II高。主要原因在于copula分布估计算法局部求精能力上相对较弱,BP算法又相对容易陷入局部最小值。 表2 Wine数据库四种方式优化结果比较Tab.2 The result comparisons of four ways ofoptimization on Wine database 第二,模式Ⅰ和模式Ⅱ比较,模式Ⅱ的精度要高于模式Ⅰ,其原因在于,模式Ⅱ的混合方式,使得BP算法和copula分步估计算法更加紧密的联系。每一次进入BP算法可以提高局部优化能力,每进入一次copula分布估计算法可以提高全局性,模式Ⅰ是一次进入copula分布估计算法再进入BP算法,模式Ⅱ是多次进入两个算法。所以模式Ⅱ在全局和局部优化能力上都有了很大的提高。 Copula理论将多元联合分布函数分解为一元的分布函数和反映它们之间联系的一个copula函数,将copula理论用于分布估计算法中,可以简化分布估计算法在估计概率分布模型时的操作并减少在该阶段所需的时间花费,copula分布估计算法具有全局优化搜索能力,BP算法的局部求精特点,将两者结合起来可以有效的避免易陷入局部最小值的缺陷。 参考文献: [1] 田雨波.混合神经网络技术[M].北京:科学出版社,2009. [2] 王美玲,王念平,李晓.BP神经网络算法的改进及应用[J].计算机工程与应用,2009,45(35):47-48. [3] 李松,刘力军,翟曼.改进粒子群算法优化BP神经网络的短时交通流预测[J].系统工程理论与实践,2012,32(9):2045-2049. [4] 李建珍.基于遗传算法的人工神经网络学习算法[J].西北师范大学学报,2002,38(2):33-37. [5] HAUSCHILD MARK,PELIKAN MARTIN.An Introduction and Survey of Estimation of Distribution Algorithms[R].Missouri Estimation of Distribution Algorithms Laboratory,2011,Medal Report No.2011004. [6] 周树德,孙增圻.分布估计算法综述[J].自动化学报,2007(2):113-124. [7] 周晓燕.基于分布估计算法的人工神经网络优化设计[J].微计算机信息,2005,2(10-3):130-131,195. [8] NELSEN R B.An Introduction to Copulas[M].Second Edition.Springer,2006. [9] ROGELIO SALINAS-GUTIERREZ,ARTURO HERNANDEZ-AGUIRRE,ENRIQUE R.Villa-Diharce.Using Copulas in Estimation of Distribution Algorithms[J].Advances in Artificial Intelligence Lecture Notes in Computer Science,2009,5845:658-668. [10] 曾建潮,崔志华.自然计算[M].北京:国防工业出版社,2012. [11] 王丽芳.copula分布估计算法[M].北京:机械工业出版社,2012. [12] 王丽芳,曾建潮,洪毅.利用Copula函数估计概率模型并采样的分布估计算法[J].控制与决策,2011,26(9):1333-1338.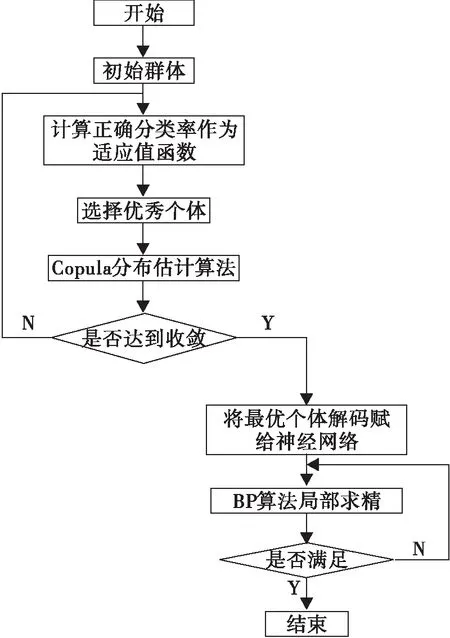
3 实验
3.1 实验数据集
3.2 实验过程
3.3 实验结果与分析

4 结束语

