地震动摆动分量对高层建筑结构的影响

楼梦麟杨明珏

（同济大学土木工程防灾国家重点实验室，上海200092）

地震动摆动分量对高层建筑结构的影响

楼梦麟*杨明珏

（同济大学土木工程防灾国家重点实验室，上海200092）

地震时地面运动是复杂的多维运动，它对结构及其构件的作用是空间的，因此建筑结构在地震动作用下是复杂的空间振动。地震动对结构的动力作用不仅产生三个平动分量的作用，也产生三个转动分量的作用。目前超限高层建筑结构的设计已逐渐开始考虑地震动转动分量的影响，但多针对扭转分量，对摆动分量研究较少。以上海中心大厦为典型，建立超高层结构的三维有限元模型。通过基岩地震波输入下的场地地震反应分析获得结构底部地震动输入的水平分量和摆动分量。运用一致输入的方法输入地震动水平分量，运用多点激励的方法输入地震动摆动分量，分别计算地震动水平输入与摆动输入时结构的地震反应，通过比较结构在这两种输入时的地震反应，探讨地震动摆动分量对高层建筑结构的影响。

高层建筑结构，多维地震动，多点激励，摆动分量，水平分量，地震动

1 引 言

近年来，高层建筑在世界各地蓬勃发展，已成为城市现代化程度的标志之一。建筑高度越来越高，结构形式越来越复杂，已不再符合平面布置简单、规则、对称，竖向质量和刚度沿高度均匀分布的要求，而形成了各种高度超限、平面和竖向不规则的复杂结构。超限建筑、复杂建筑对抗震设计极其不利，地震灾害会给高层建筑带来巨大经济损失。

迄今为止，强震观测的主要对象只是地震动三个正交的平动分量。事实上，地震波通过地面时的运动是极其复杂的，各点的波速、周期和相位是不同的。由于地面质点间运动的差别，地震动对结构的动力作用不仅产生三个平动分量的作用，也产生三个转动分量的作用，结构在地震动作用下是复杂的空间振动［1，2］。大量震害现象也证明了这一点，如1964年的Alaska地震，转动分量的影响导致地面沉降达2.5 m；在Corinth海湾地震中，转动分量使地面产生明显的南北向转动［3］。

基于以上原因，专家学者们在研究超限高层结构的抗震设计时，逐渐开始考虑地震动对结构产生的转动分量作用的影响［4］，而三个转动分量中，对于扭转分量的研究较多［5-7］，对于摆动分量的研究较少。本文通过对实际工程地震反应的分析，运用多点激励的输入方法［8］，比较地震动水平一致输入与考虑地震动产生的摆动作用输入时结构的反应，分析地震动摆动分量对高层建筑结构的影响。

2 工程对象及分析方法

2.1 上海中心大厦工程概况

上海中心大厦位于浦东陆家嘴功能区，为多用途开发项目，是目前国内在建的最高建筑，建筑结构高度580 m，总高度632 m。其中地面以上为151层，地下为4层，上部主体结构可依照8个加强层分为9个区。该建筑采用混凝土核心筒、巨型框架、外伸刚臂组合的结构形式，自振周期近10 s。本文根据相关工程资料，用ANSYS有限元软件建立简化的上海中心结构模型，并且将结构地下部分简化为直径100 m、深度30 m的圆形刚性基础底盘。土层作用采用弹簧单元模拟。有限元计算模型共11 934个节点，18 517个单元。三维有限元模型如图1所示。

2.2 地震动输入参数

根据实际场地条件，建立上海中心场地三维有限元土层模型，土层计算深度取250 m，水平X方向取10倍深度即2 500 m，Y方向取200 m。土层模型中间为刚性基础底盘所在位置，基坑深度30m。为简化计算规模，计算时考虑对称性，只取一半模型进行计算，如图2所示［9，10］。

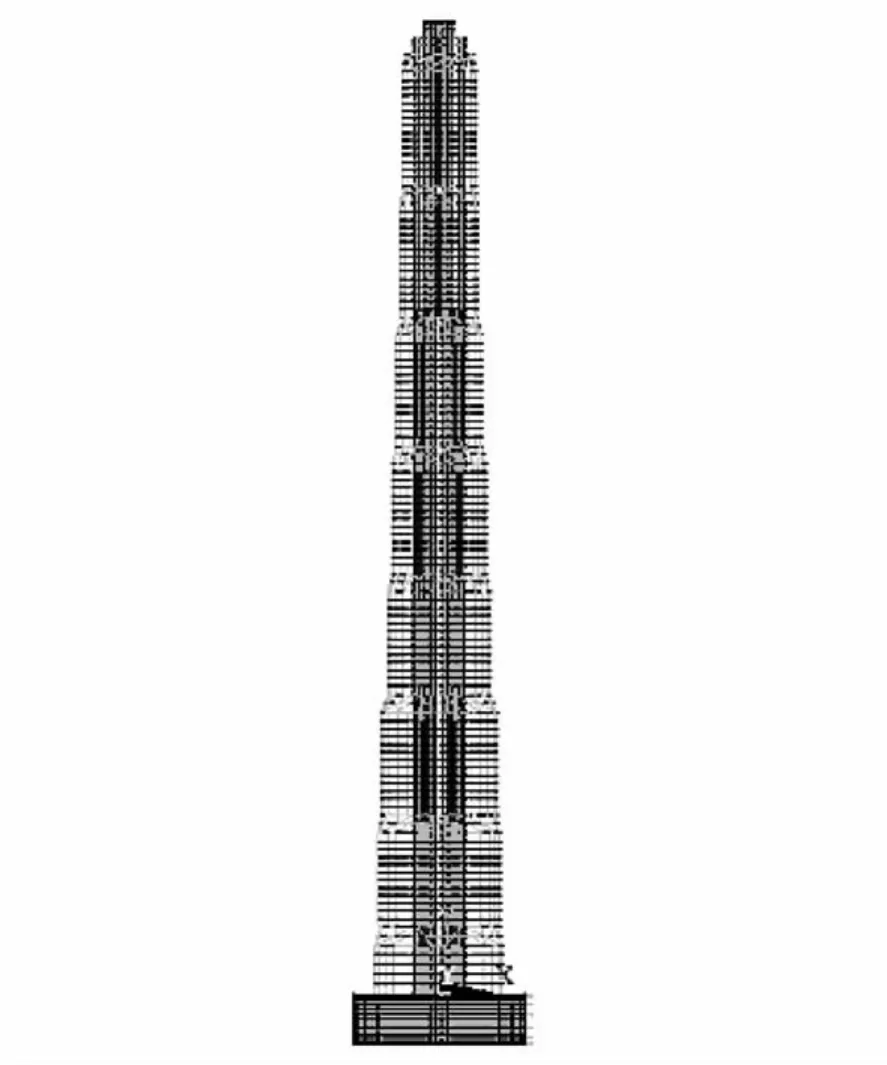
图1 结构有限元模型Fig.1 Finite elementmodel

图2 上海中心场地计算模型Fig.2 Sitefield model of the Shanghai Tower Site

根据上海中心大厦项目工程场地地震安全性报告相关数据资料，在土层模型的基岩面输入50年超越概率水平为2%的基岩地震波，峰值加速度为1.934 m／s2。计算得到基坑地面位置处13个节点的水平加速度时程和竖向加速度时程，如图3所示。这些位置节点的反应结果即为结构基础底盘底部的地震动输入。其中，水平加速度时程作为地震动水平分量输入。各位置节点的竖向加速度时程使得基础底盘明显表现出摆动特征，因而可作为地震动摆动分量输入。

2.3 计算分析方法

本文共有三种工况。

工况1：地震动水平一致输入。即基础底盘各点同时输入水平加速度时程。

工况2：地震动摆动分量输入。即根据上述得到的13个位置节点的竖向加速度时程，用线性内插和多点激励的输入方法，向基础底盘各节点输入相应的竖向加速度时程，从而模拟摆动输入。图4和图5为按照此方法输入后，刚性基础底盘顶面（即上部结构底部）的竖向加速度峰值和竖向位移峰值，可见呈明显摆动特征。

工况3：同时考虑地震动水平分量输入与摆动分量输入。

分别计算上述工况，比较各工况下的反应结果，分析地震动摆动分量对高层建筑结构的影响。

图3 刚性基础底盘及位置节点Fig.3 Rigid base and node position

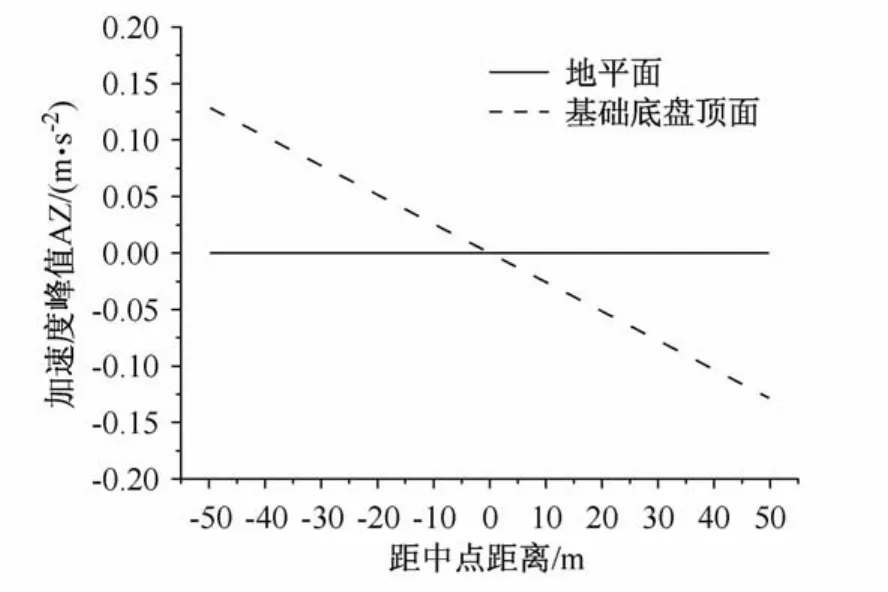
图4 基础底盘顶面竖向加速度峰值Fig.4 Vertical acceleration peak values at the base top surface

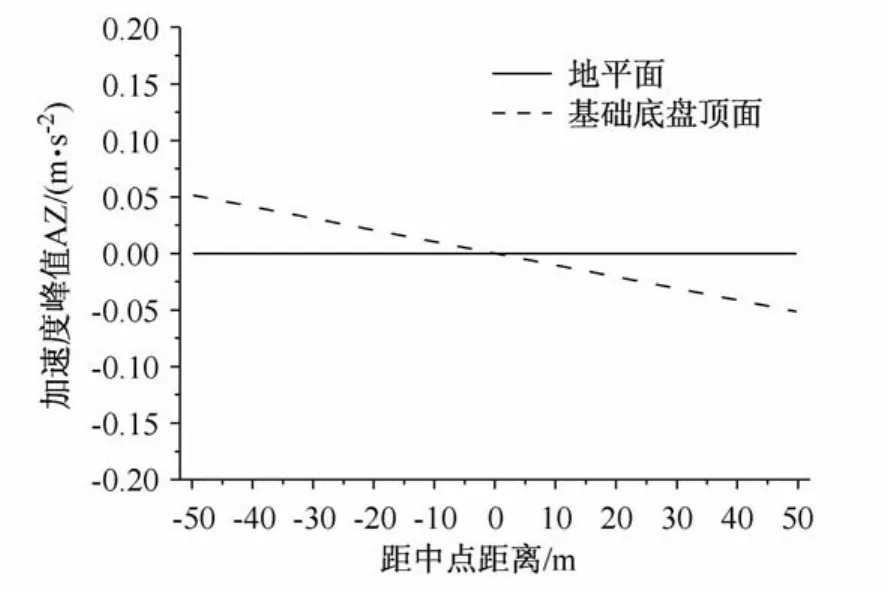
图5 基础底盘顶面竖向位移峰值Fig.5 Vertical displacement peak values of the base top surface

3 地震动摆动分量对结构地震反应的影响

3.1 地震动摆动分量对结构顶层加速度反应的影响

地震动水平输入、摆动输入和同时输入时结构顶层水平加速度的时程如图6所示，峰值分别为0.659 m／s2（水平输入），0.535 m／s2（摆动输入），0.892 m／s2（同时输入）。可见，仅考虑摆动输入时产生的顶层加速度比水平输入时小。但同时输入时顶层加速度增大，峰值比水平输入时的峰值大35%。

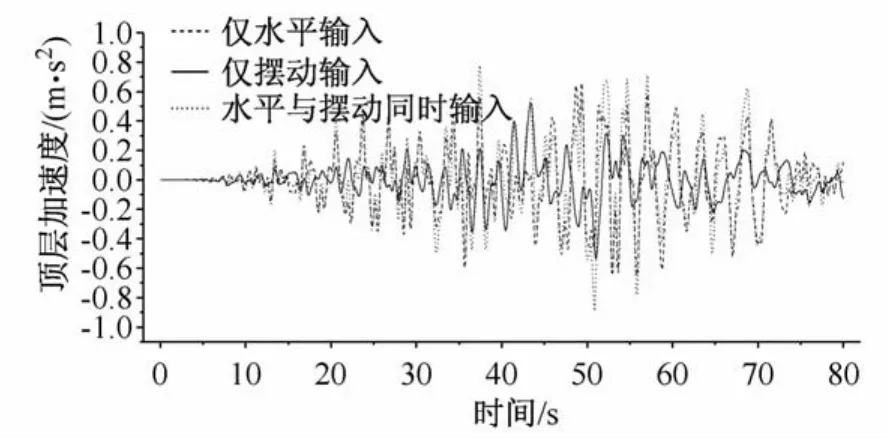
图6 结构顶层水平加速度时程Fig.6 Horizontal acceleration of the top floor of the strnctuve

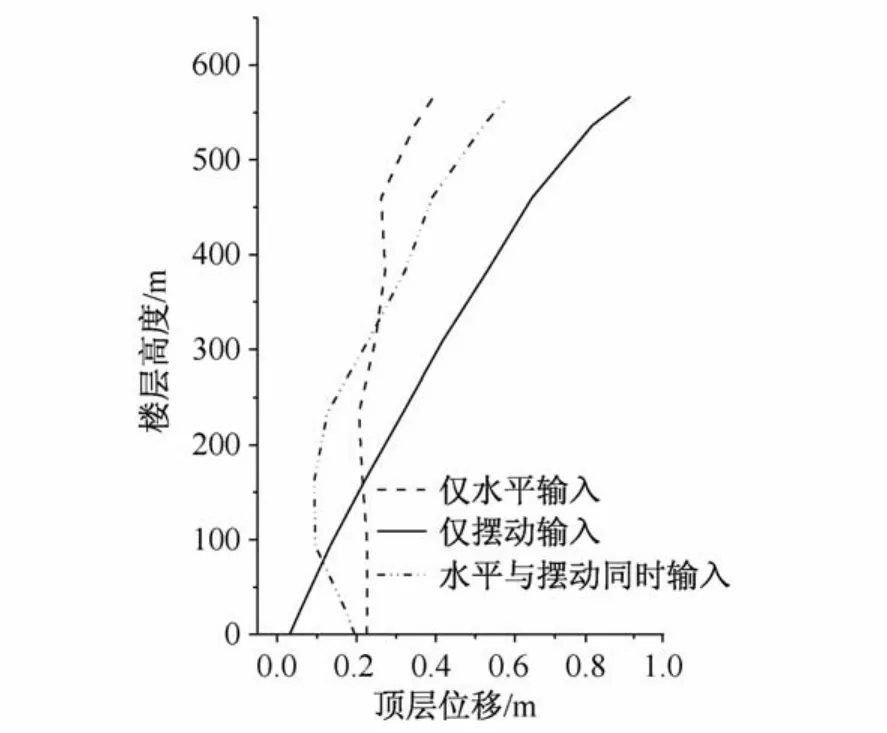
图7 结构各层水平位移峰值Fig.7 Horizontal displacement peak values of the different floors of the strnctuve

3.2 地震动摆动分量对结构各加强层位移峰值的影响

地震动水平输入、摆动输入和同时输入时结构各加强层水平位移峰值如图7所示。摆动分量作用减小了较低楼层的水平位移而增大了较高楼层的水平位移。结构顶层水平位移峰值分别为0.395 m（水平输入），0.890 m（摆动输入），0.581 m（同时输入）。可见，摆动作用增大了顶层的水平位移峰值。同时输入时顶层水平位移峰值比水平输入时增大47%，但小于仅摆动输入时的情况。

图8为水平输入和摆动输入时，各加强层水平总位移、刚体位移和弹性位移。总位移是刚体位移与弹性位移的叠加。

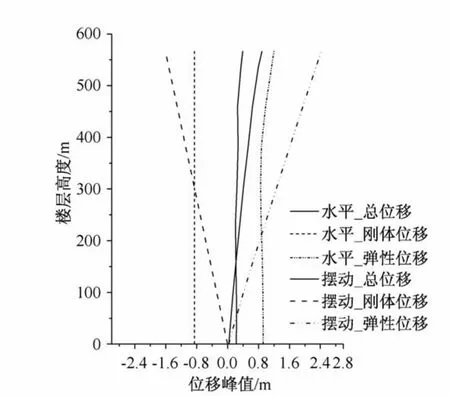
图8 各层水平总位移、刚体位移、弹性位移Fig.8 Total displacement，rigid displacement and elastic displacement of the different floors

3.3 地震动摆动分量对结构各区层间位移的影响

本文以结构各区加强层为研究对象，因此本节中的层间位移定义为相邻加强层之间的层间位移。考虑地震动摆动作用前后，结构层间位移如表1所示。由表中数据可知，摆动作用增大了楼层层间位移幅值，且对于较低楼层的增大作用较大，最大为增大1.89倍；而对于较高楼层的增大作用较小。图9中摆动输入时的层间位移已扣除了由于摆动的刚体位移引起的层间位移，所以此部分层间位移为引起结构构件内力的弹性层间位移。而水平输入时，由于水平刚体位移不引起层间位移，所以此水平层间位移即为弹性层间位移。弹性层间位移是产生结构构件内力的原因。由图9可见，摆动输入时结构的弹性层间位移大于水平输入时结构的弹性层间位移，因此地震动摆动分量引起的结构内力大于水平分量引起的结构内力。摆动分量对结构地震内力的影响情况见下节分析。

表1 结构层间位移Table 1 Inter-story drift of the strcuture m

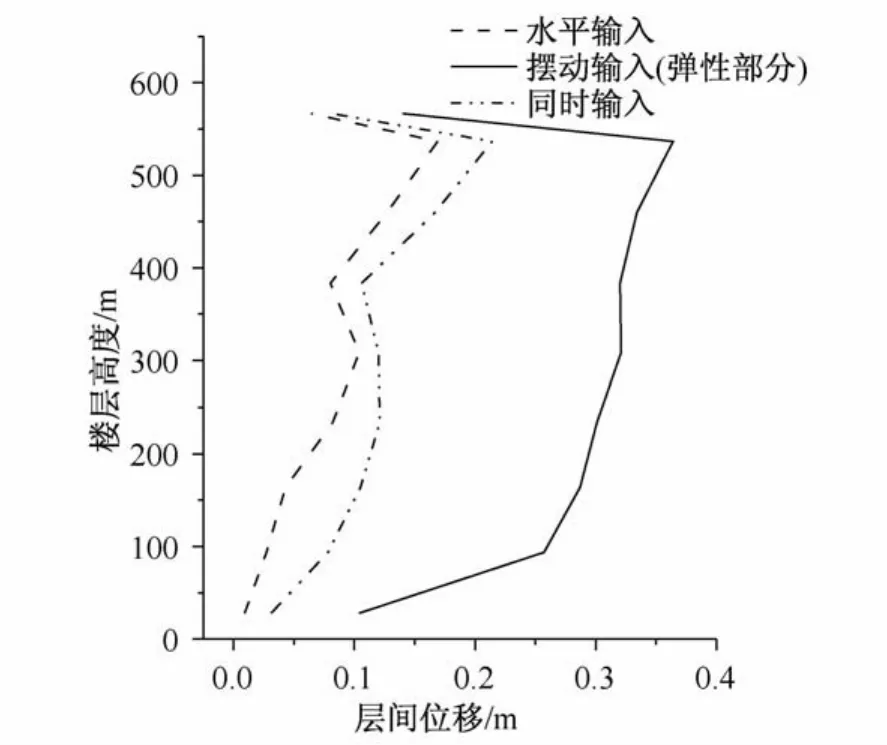
图9 结构层间位移Fig.9 Inter-story drift of the structure

4 地震动摆动分量对地震作用下结构地震内力的影响

本节提取典型结构构件内力：柱底剪力、弯矩、剪力墙剪力，连梁弯矩、进行内力比较。作为分析对象的构件均为各加强层位置处相应的构件。需说明的是，以下内力值均未与重力作用下结构内力值进行组合，仅为地震作用产生的内力。

4.1 地震动摆动分量对柱底剪力和弯矩的影响

提取3种工况下各加强层下方柱柱底的剪力和弯矩进行比较，结果如图10、图11和图12所示。

对于各层柱底轴力，考虑地震动摆动输入后，剪力比水平输入时有所增大。增幅在2、3加强层处较为明显，最大增幅为67%，即峰值从水平输入的22 640 kN增大为同时输入的37 900 kN，其余各加强层处柱底轴力与水平输入时相比均有增大。

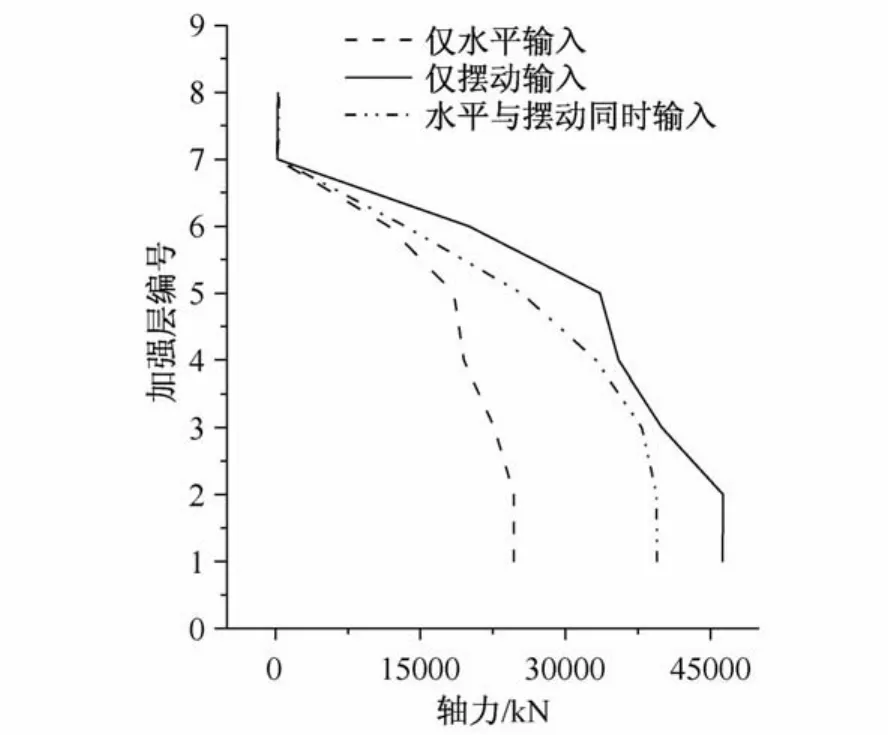
图10 柱底轴力峰值Fig.10 Peak value of column axial force

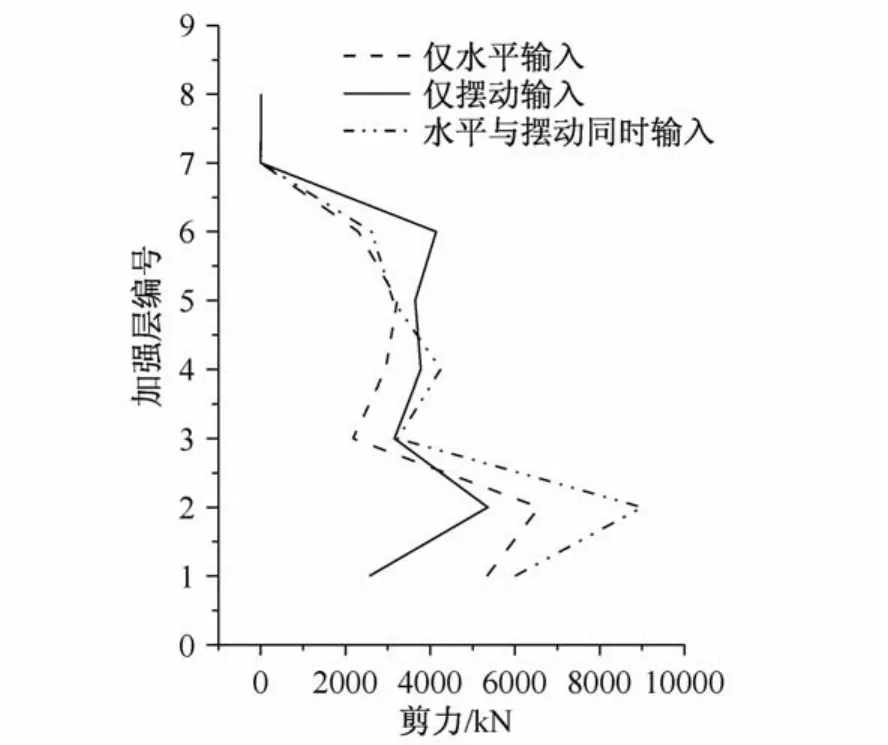
图11 柱底剪力峰值Fig.11 Peak value of column shearing force

图12 柱底弯矩峰值Fig.12 Peak value of columnmoment

对于各层柱底剪力，考虑地震动摆动输入后，剪力比水平输入时有所增大。增幅在第3、第4加强层处较为明显，最大增幅为48%，即峰值从水平输入的2 180 kN增大为同时输入的3 230 kN，其余各加强层处柱底剪力与水平输入时相当或稍有增大。

对于各层柱底弯矩，考虑地震动摆动输入后，弯矩比水平输入时有所增大。增幅也是在第3、第4加强层处较为明显，最大增幅为57%，即峰值从水平输入的8 940 kN·m增大为同时输入的14 100 kN·m，其余各加强层处柱底弯矩与水平输入时相当或稍有增大。

4.2 地震动摆动分量对剪力墙剪力的影响

图13为各工况下各加强层中剪力墙平面内剪力峰值。

考虑地震动摆动输入后，剪力墙中剪力比水平输入时有所增大。低楼层剪力增幅比高楼层明显，最大增幅在底层出现，为55%，即峰值从水平输入的2 490 kN增大为同时输入的3 870 kN，其余各加强层处剪力墙剪力与水平输入时相当或稍有增大。

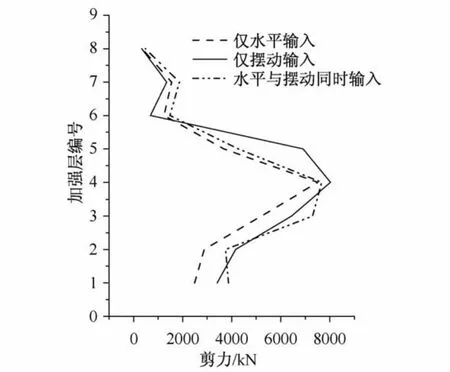
图13 剪力墙剪力峰值Fig.13 Peak value of shear wall shearing force

4.3 地震动摆动分量对连梁弯矩的影响

图14为各工况下各加强层中连梁的弯矩峰值。

考虑地震动摆动输入后连梁中弯矩比水平输入时有所增大。低楼层剪力增幅比高楼层明显，最大增幅在第3加强层出现，为51%，即峰值从水平输入的8 580 kN·m增大为同时输入的13 000 kN·m，其余各加强层处连梁弯矩与水平输入时相当或稍有增大。

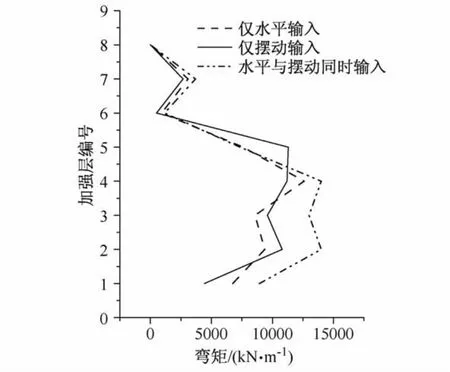
图14 连梁弯矩峰值Fig.14 Peak value of coupling beam moment

4.4 摆动分量引起结构地震内力变化的原因

以第5加强层中剪力墙剪力为例，说明摆动分量影响结构内力的原因。图15为3种工况下的剪力时程。可见，水平输入与摆动输入时产生内力的相位相反，且摆动分量产生的内力更大一些，这与3.3节中分析情况一致。因此叠加之后，内力峰值与水平输入时相比，相当或有所增大，这就是摆动分量对结构地震内力造成影响的原因。

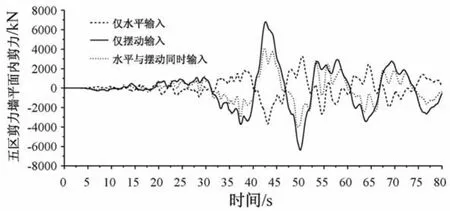
图15 第5加强层剪力墙剪力时程Fig.15 Shear wall shearing force of the fifth reinforced floors

5 结 论

本文通过计算上海中心大厦简化模型在地震作用下的反应，分析了地震动摆动分量对高层建筑结构的影响。主要得到以下结论：

（1）地震动摆动分量会增加结构顶层水平加速度反应，峰值增幅为35%。

（2）摆动分量减小了较低楼层的位移反应而增大了较高楼层的位移反应，且会产生较大的顶层水平位移。考虑摆动输入后顶层水平位移峰值比水平输入时增大47%，为0.581 m。

（3）考虑地震动摆动分量作用后，结构各区层间位移均有增大，最大增幅为增大1.89倍。摆动输入引起的弹性层间位移大于水平输入引起的弹性层间位移，因此也引起较大内力。

（4）仅地震动摆动分量造成的结构地震内力大于仅水平分量造成的结构地震内力值，实际地震内力为两者的反向叠加。

（5）摆动分量对结构中产生地震内力有增大的影响，增幅较大的为1～4加强层，即较低楼层处。在较高楼层处内力仅稍有增大或与水平输入时相当。

［1］ 李杰，李国强.地震工程学导论［M］.北京：地震出版社，1992.Li Jie，LiGuoqiang.Introduction to earthquake engineering［M］.Beijing：Earthquake Press，1992.（in Chinese）

［2］ 李宏男.结构多维抗震理论与设计方法［M］.北京：科学出版社，1998.Li Hongnan.Theoretical analysis and design of structures tomultiple earthquake excitations［M］.Beijing：Science Press，1998.（in Chinese）

［3］ Tselentis G A.，Makropoulos K C.Rates of crustal deformation in the gulf of Corinth（central Greece）as determined from seismicity［J］.Tectonophysics，1986，124（1-2）：55-57，61-66.

［4］ 何超，罗奇峰，洪钟，等.关于地震动转动分量的研究［J］.地震研究，2011，34（1）：81-87.He Chao，Luo Qifeng，Hong Zhong，et al.Brief discussion on the study of the seismic rotational components［J］.Journal of Seismological Research，2011，34（1）：81-87.（in Chinese）

［5］ 徐培福，黄吉锋，韦承基，等.高层建筑结构在地震作用下的扭转振动效应［J］.建筑科学，2000，16（1）：1-6.Xu Peifu，Huang Jifeng，Wei Chengji，et al.Response of torsional vibration of tall building structures induced by seismic action［J］.Building Science，2000，16（1）：1-6.（in Chinese）

［6］ 刘跃伟，李宏男.地震动的扭转分量与结构的扭转地震作用［J］.工程力学，2012，（11）：103-108.Liu Yuewei，Li Hongnan.Torsional earthquake ground motion and torsional earthquake inputof building［J］.Engineering Mechanics，2012，（11）：103-108.（in Chinese）

［7］ Newmark N M.Torsion in symmetrical buildings［C］.Proc.Fourth World Conference on Earthquake Engineering，Chile，1969.

［8］ 江洋，石永久，王元清，等.实用多点输入虚拟激励法在通用有限元软件中的实现［J］.地震工程与工程振动，2010，30（1）：46-52.Wang Yang，Shi Yongjiu，Wang Yuanqing，et al.Implementation of the practical pseudo excitation method formulti-support seismic response analysis in general FEM software［J］.Journal of Earthquake Engineering and Engineering Vibration，2010，30（1）：46-52.（in Chinese）

［9］ 张如林，楼梦麟，徐奴文，等.基于子结构技术的圆形地下连续墙场地动力反应分析［C］.第七届全国土木工程研究生学术论坛论文集，2009：1-4.Zhang Rulin，Lou Menglin，Xu Nuwen，et al.Dynamic response analysis of the site with circular diaphragm wall based on substructure technique［C］.Symposium of the 7th National Civil Engineering Graduate Students Academic Forum，2009：1-4.（in Chinese）

［10］ 楼梦麟，潘旦光，范立础，等.土层地震反应分析中侧向人工边界的影响［J］.同济大学学报（自然科学版），2003，31（7）：757-761.Lou Menglin，Pan Danguang，Fan Lichu，et al.Effect of vertical artificial boundary on seismic response of soil layer［J］.Journal of Tongji University（Natural Science），2003，31（7）：757-761.（in Chinese）

Influence of Rocking Earthquake Ground M otion on Super High-rise Structures

LOU Menglin*YANG Mingjue
（State Key Laboratory of Disaster Reduction in Civil Engineering，Tongji University，Shanghai200092，China）

Earthquake ground motion is a complex andmulti-dimensionalmovement，which has a spatial effecton the structure and its components.The structure is under complex spatial vibration under earthquake ground motions.The dynamic action caused by earthquake ground motions on the structures not only produces three translational components，but italso produces three rotational components.The influence of rotational components on seismic responses of the super high-rise structures is considered nowadays，butwith a focus on torsional component instead of rocking component of the three rotational components.In this paper，a three-dimensional finite element modelwas established to simulate the super high-rise structure of Shanghai Tower.The horizontal and rocking component of earthquake ground motion at the bottom of the structure were acquired through the site analysiswith bedrock seismic wave input.Seismic responses of the structure under horizontal excitation were calculated with the uniform excitation method while seismic responses of the structure under rocking excitation were calculated with themultiple point excitationmethod.By comparing the seismic responses under different excitation situations，the influence of rocking earthquake ground motion on super high-rise buildings is discussed.

dssuper high-rise structure，multi-dimensional earthquake vibration，multiple point excitation，rocking component，horizontalcomponent，earthquake ground motion

2013－05－07

科技部国家重点实验室基础研究资助项目（SLDRCE08－B－01）

*联系作者，Email：lml＠tongji.edu.cn