基于ANSYS软件钢筋混凝土框架结构多尺度数值分析

吴 强钱 江黄 维

（1.同济大学土木工程防灾国家重点实验室，上海200092；2.同济大学结构工程与防灾研究所，上海200092）

基于ANSYS软件钢筋混凝土框架结构多尺度数值分析

吴 强1，2，*钱 江1，2黄 维1，2

（1.同济大学土木工程防灾国家重点实验室，上海200092；2.同济大学结构工程与防灾研究所，上海200092）

根据能量守恒与材料力学原理，提出一种几何多尺度数值计算模型。采用ANSYS软件对一12层钢筋混凝土框架结构振动台试验进行了多尺度数值模拟，同时利用梁单元模型模拟来作对比分析，计算了结构的动力特性与地震动力时程响应。分析结果对比显示，多尺度模型模拟结果与梁单元模型模拟结果和振动台试验结果具有较高的吻合度，为以后结构分析计算提供了一种简单有效的手段。

多尺度模型，ANSYS软件，钢筋混凝土框架结构

1 引 言

图1 底层柱底破坏Fig.1 Ground floor column damages

历次地震震害表明，钢筋混凝土框架结构在地震作用下的破坏往往是局部的破坏，整体结构因局部破坏而失去抗震能力，进而倒塌。1979年10月15日美国帝谷地震（6.5级），加州埃尔森特罗帝国郡服务大楼，为6层钢筋混凝土框架-剪力墙结构，由于刚度沿竖向分布不均，底层一侧的4个边柱发生弯剪破坏（图1），柱底混凝土大块剥落，纵向钢筋严重屈曲，水平箍筋拉屈［1］。2005年10月8日的克什米尔大地震（7.6级），Ryadh中心为钢筋混凝土框架结构，结构建造较早，没有进行抗震设计。柱的混凝土强度不够，配筋不足，在二层柱两端出现塑性铰［2］（图2）。

图2 柱端破坏Fig.2 Column end damage

从以上的实际震害可以看到，钢筋混凝土框架结构在地震作用下的破坏一般为集中在梁柱节点处的局部破坏，局部破坏的累计最终导致整体结构的失效。但目前常用的工程非线性分析主要分为基于宏观单元的整体结构非线性分析和基于实体单元的局部结构非线性分析。宏观模型主要采用杆、壳等单元，计算量小，却不能反映结构的破坏微观机理，如结构的局部失稳、节点破坏、接触问题等。而基于实体单元的微观分析，虽然可以较好地把握结构的局部破坏过程，但由于计算量加大，收敛性较差而受到限制。而从整体结构中取出局部构件进行实体模型分析，故目前迫切需要兼顾结构局部破坏和结构整体受力行为的计算模型，多尺度计算模型就是解决该问题的有效方法。

工程结构中的多尺度模型主要对不同尺度的力学行为采用不同的单元进行模拟，进而组合成多尺度有限元模型。例如在结构整体模型中，对局部破坏部分用实体单元模拟，对无破坏或破坏较小部分用梁单元或壳单元模拟。国内外学者对多尺度模型进行了一定的研究［3-5］，岳健广等［3］采用ABAQUS软件，建立了3D／1D的多尺度模型耦合关系，并与试验结果对比，结果表明该方法能较好地模拟结构的局部破坏；陆新征等［5］采用MSC.MARC软件提供的节点局部坐标系和用户自定义子程序功能，实现了不同尺度单元界面的连接。而对于常用的大型通用有限元软件ANSYS还没有相关学者进行研究。本文将对不同单元之间的协同作用进行分析，建立不同尺度单元间的约束方程，在ANSYS软件中建立钢筋混凝土框架结构多尺度有限元模型进行数值分析。

2 不同尺度模型的界面连接

多尺度计算的难点是不同尺度单元模型之间界面连接的合理性，常见的不同尺度单元的连接情况有三种：梁单元模型与壳单元模型、梁单元模型与实体单元模型、壳单元模型与实体单元模型之间的连接。本文以梁单元模型与实体单元模型连接为例，说明界面连接的原理与方法。

2.1 梁单元与实体单元耦合

结合有限元分析软件ANSYS，梁—实体单元耦合可通过多点约束方程实现，其统一形式为

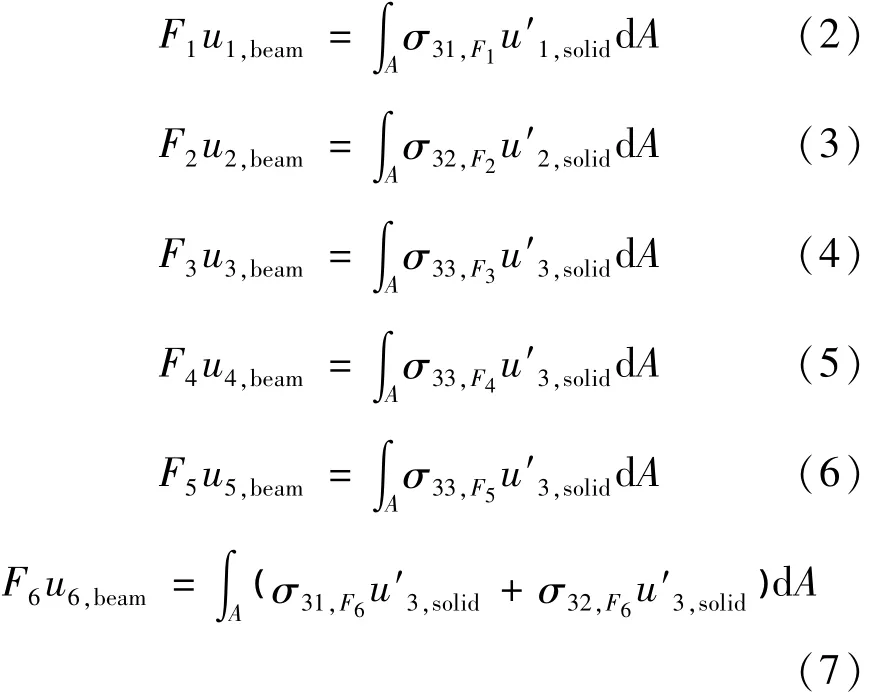
式中，F1，F2为作用在梁单元上剪力在1轴、2轴的分量，F3为作用在梁单元上轴力，F4，F5为作用在梁单元弯矩在1轴、2轴的分量，F6为作用在梁单元上的扭矩；σ31，Fi，σ32，Fi，σ33，Fi分别为界面处实体单元节点在1轴、2轴、3轴由Fi引起的应力分量（可由材料力学计算）；A为耦合界面的面积；ui，beam为梁单元节点位移在耦合界面各轴的分量，u′i，solid为实体单元节点位移在耦合界面各轴的分量（图3）。

2.2 界面连接算例

根据以上原理，本文通过ANSYS软件中提供的接触单元和MPC技术建立满足式（2）—式（7）的多尺度耦合约束方程［6］，实现模型的结构多尺度建模计算分析，下面通过一个小算例来验证这种方法。

式中，u为梁单元节点自由度；u′为实体节点自由度；n为实体单元节点总数；Xi为耦合界面上节点i的约束系数，与实体单元型函数相关。

如图3所示，通过耦合界面上不同单元节点在各项合力作用下作功相等建立约束方程如下：

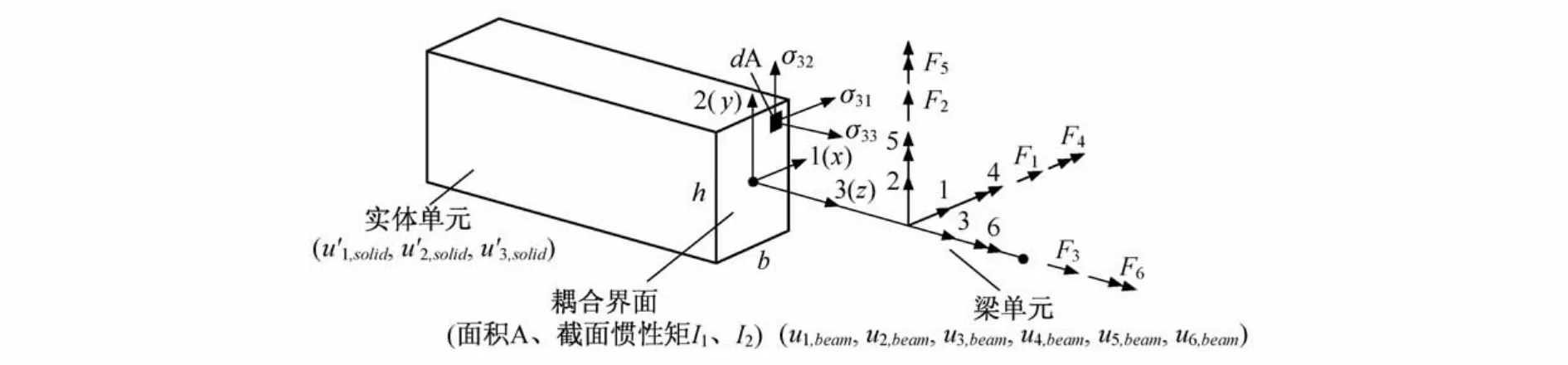
图3 梁—实体单元的耦合Fig.3 Coupling of beam element and solid element

图4 （a）所示的等截面悬臂柱，几何尺寸为300 mm×400 mm×2 000 mm，材料弹性模量取2.11×1011N／m2，屈服强度取10 MPa，无材料强化，受到水平荷载P＝50 kN，本文分别以梁单元-实体单元建立多尺度模型，如图4（b）所示；采用实体单元建立该柱的微观模型，如图4（c）所示。在ANSYS软件中，梁单元采用BEAM188单元，实体单元采用SOLID65单元。主要分析结果参见表1，两种计算模型的应力云图参见图5。

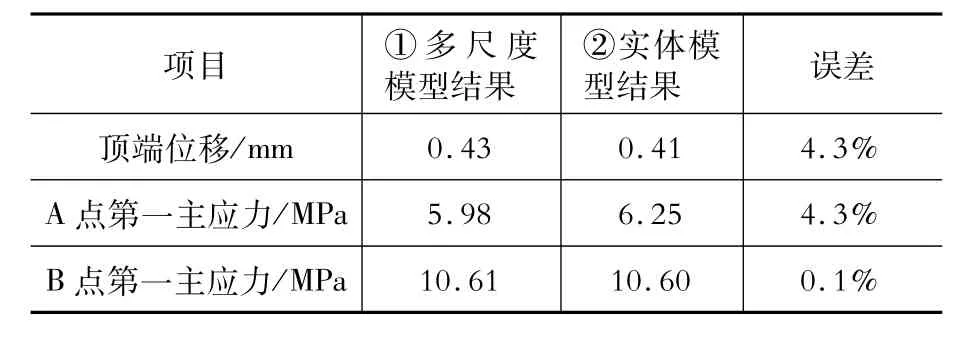
表1 两种计算模型计算结果Table 1 Computing result of two com puting m odels

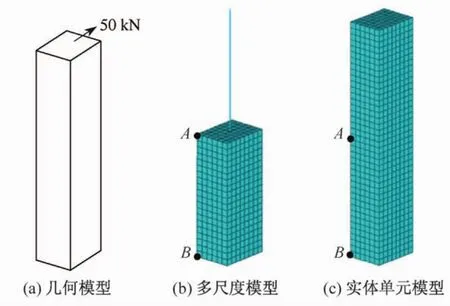
图4 几何模型及有限元计算模型Fig.4 Geometrymodel and finite elementmodels

上述结果数据表明，多尺度模型计算结果与实体单元模型计算结果具有高度的吻合性，多尺度模型耦合界面上不同单元界面上的应力吻合度也很高。说明本文建议的界面连接方法可以实现梁单元宏观模型与实体单元细观模型的不同尺度间的过渡，从而可以将精细模型植入整个宏观梁单元模型结构中进行多尺度结构计算。

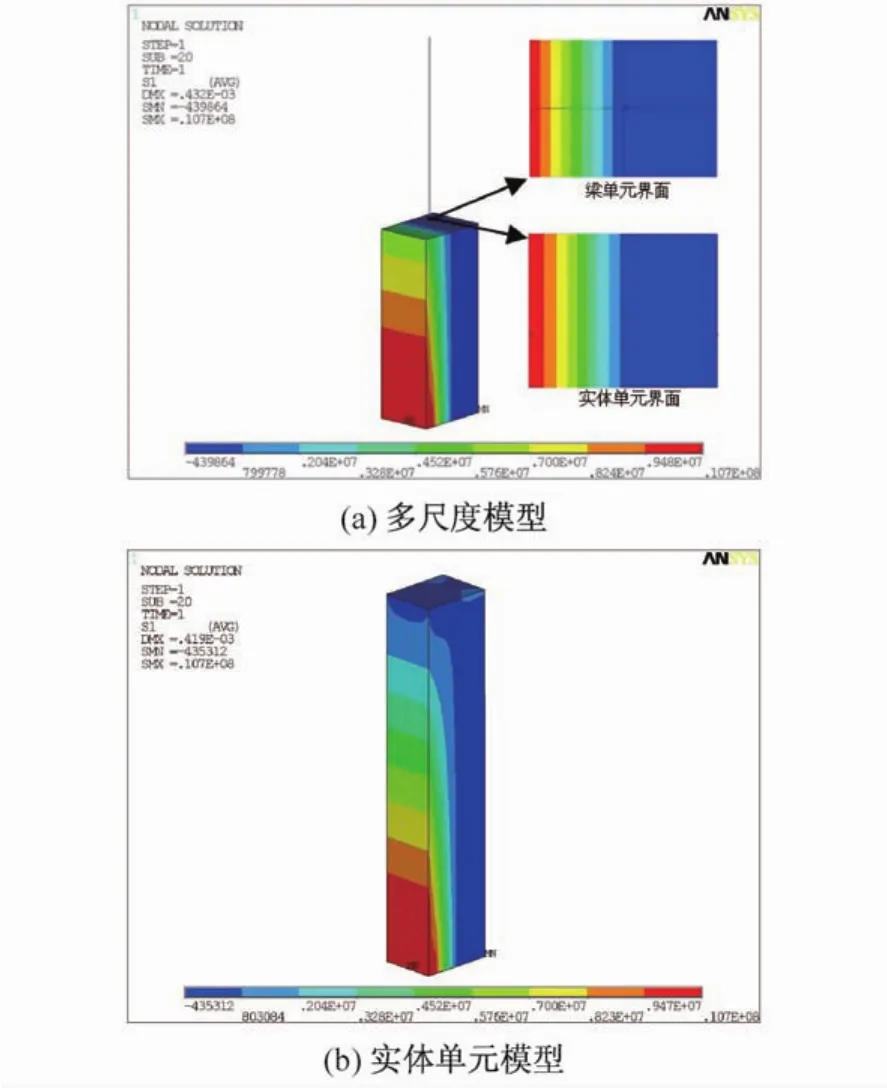
图5 两种计算模型的应力云图Fig.5 Stress nephogram of two computingmodels

3 多尺度钢筋混凝土框架结构计算模型

3.1 框架信息及模型介绍

选取同济大学国家重点实验室的12层钢筋混凝土框架［7］，本文建立两个模型，一个采用梁单元建立的模型，称为BM模型；一个采用本文提出的多尺度方法采用梁单元和实体单元建立的多尺度模型，称为MSM模型。结构两个方向均为单跨，跨度为6 m，层高为3 m，梁截面尺寸为300 mm×600 mm，柱截面尺寸为500 mm×600 mm，楼板厚度为120 mm，混凝土强度等级为C30，梁截面配筋为6D22，上下各3根，柱截面配筋为8φ22，楼板配筋为双向φ8＠150。振动台试验模型如图6（a）所示。域梁、柱混凝土采用三维实体单元SOLID65单元，钢筋采用LINK8单元，其他区域均采用采用BEAM188单元，楼板采用SHELL63单元简化。建立多尺度模型时，梁柱构件采用实体单元SOLID65创建部分长度取l＝1.5h［8］，其中，h为构件截面高度，多尺度计算模型（MSM）如图7（b）所示，梁单元模型（BM）如图7（c）所示。

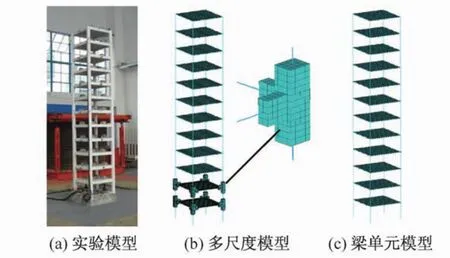
图6 试验模型和有限元模型Fig.6 Testmodel and the finite elementmodel

混凝土采用多线性随动强化模型，应力应变关系采用规范［9］建议的混凝土本构关系作为混凝土的单轴拉压应力—应变关系，其应力—应变关系可由函数表达式定义，应力—应变关系上升段、下降段参数按规范［9］附录C取值。钢筋采用双线性随动强化模型，折线第一上升段的斜率为钢筋本身的弹性模量，第二上升段为钢筋强化段，斜率取初始弹性模量的1／100。

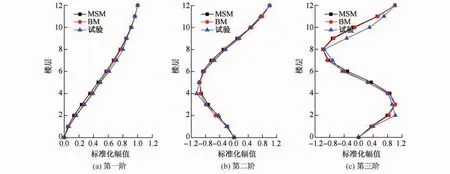
图7 X向前三阶模态Fig.7 The first threemodes at the X direction

3.2 结构动力特性分析

振动台试验对模型进行白噪声扫频得到各阶频率，并由传递函数的幅值以及相位角识别振型，白噪声扫频得到结构的频率按照相似关系Sf＝5.038，求出原型结构的频率，试验结果与有限元计算结果见表2。

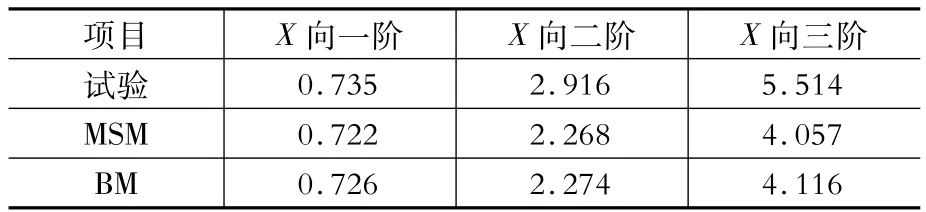
表2 结构X向前三阶自振频率对比Table 2 Com parison of the first three natural frequencies at the X direction

由MSM与BM确定的X向前3阶模态和白噪声扫频得到的模态对比见图7（模态以顶点幅值为1标准化），由此可见多尺度计算模型与梁单元计算模型确定的X向前三阶模态非常相近，与试验结果的前两阶模态比较相近，第三阶模态稍有一些差异。

3.3 结构地震响应动力时程分析

考虑到结构X方向相对较弱，响应更为剧烈，故分析主要针对X方向，取加速度峰值为0.035 g、0.10 g和0.15 g的El Centro地震波X方向分量沿结构X方向输入，进行动力时程分析，将振动台模型试验结果按照试验位移相似比Sd＝1／10推算后，得到对应原型结构的地震响应。各地震峰值加速度工况下，结构顶层位移时程曲线如图8所示，结构的最大楼层位移如图9所示，结构的层间位移如图10所示。

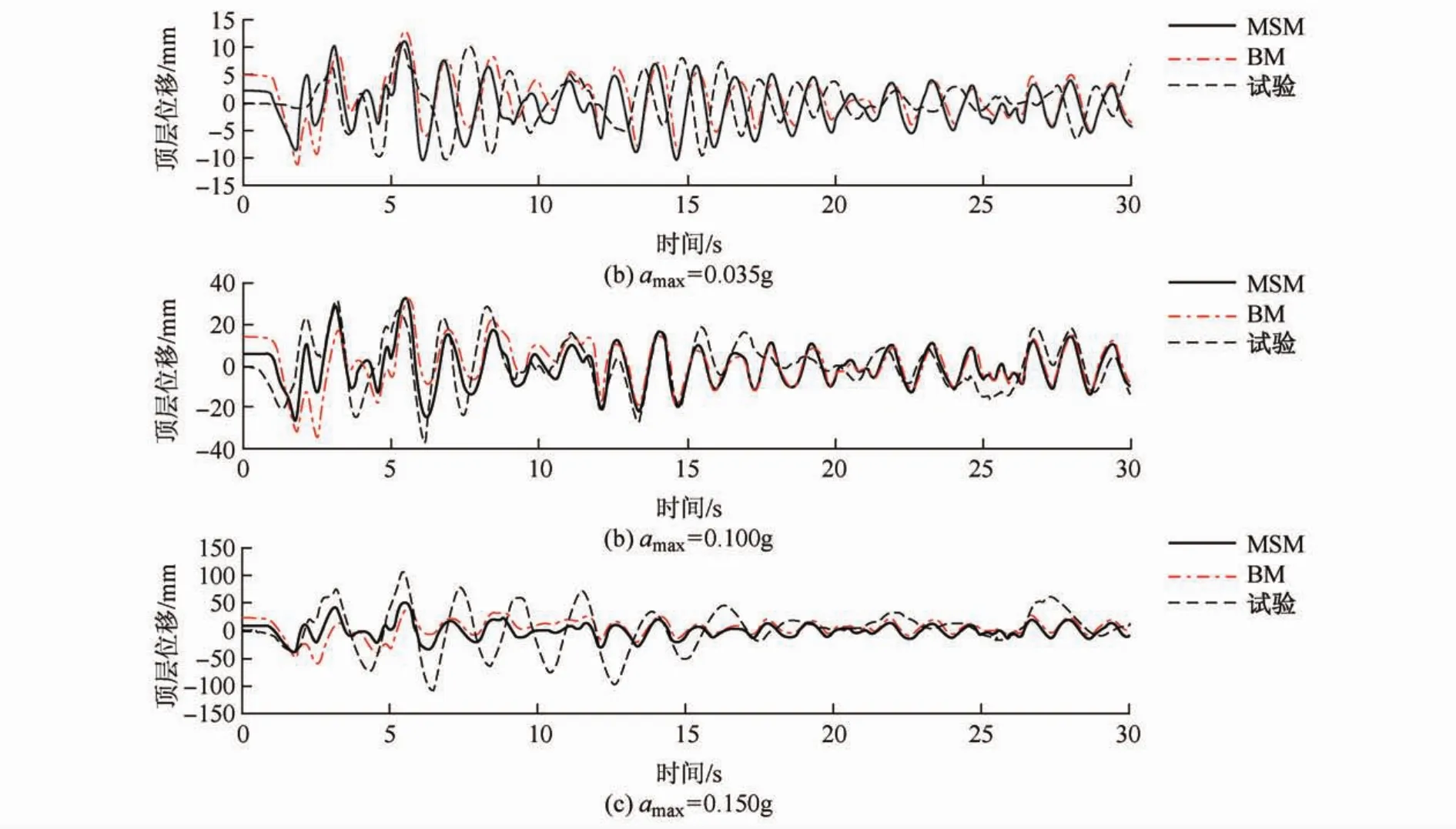
图8 顶层位移时程对比Fig.8 Comparison of the top floor＇s displacement time histories

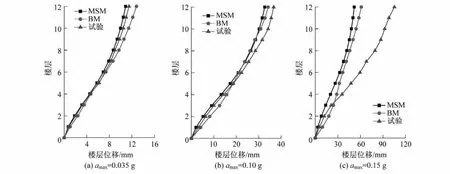
图9 最大楼层位移对比Fig.9 Comparison of themaximum floor displacements

由图8—图10可以看出，输入加速度峰值为0.035 g和0.10 g时，MSM所确定的结构顶层位移时程曲线和试验曲线在峰值上是吻合的，整个时程曲线稍有差异，这主要是因为试验所测得的是加速度时程，还需要积分得到位移时程，积分的过程中会有数据漂移从而产生差异。MSM和BM所确定的结构顶层位移时程曲线初始值比较大，这是因为时程分析时，考虑了重力的影响，而且是将重力加在第一步的地震波激励的Z方向上，即使第一步的地震波水平激励很小，但重力的施加和瞬态效应的影响，会形成一个明显的重力二阶效应，但是由于阻尼的存在，会逐渐消除这一初始值影响。MSM所确定的楼层位移和层间位移与试验值比较接近；输入加速度峰值为0.15 g时，MSM所确定的位移时程曲线和试验相差较大，楼层位移和层间位移相差也比较大，考虑到实际振动台试验时，在0.15 g El Centro波工况之前已进行了16个工况试验，造成了相当的损伤累计，刚度退化严重，是产生这种差异的原因之一。三种工况下，MSM和BM的顶层位移时程结果、最大楼层位移和层间位移的吻合度都比较高。

3.4 损伤分析

ANSYS中，混凝土通过SOLID65单元受拉开裂与受压压碎来描述混凝土材料力学损伤行为，本文提取了MSM在输入地震加速度峰值为0.10 g工况下结构底层一实体单元节点的损伤情况，参见图11（图中“O”表示受拉开裂，“×”表示受压压碎）。

由图11可以看出，混凝土受拉开裂与受压压碎均发生在梁端部处，这与振动台试验中模型的破坏情况一致。

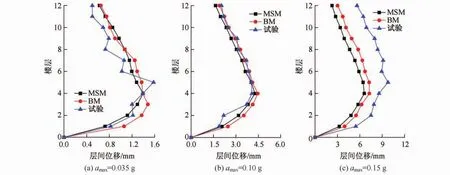
图10 层间位移对比Fig.10 Comparison of the story drifts

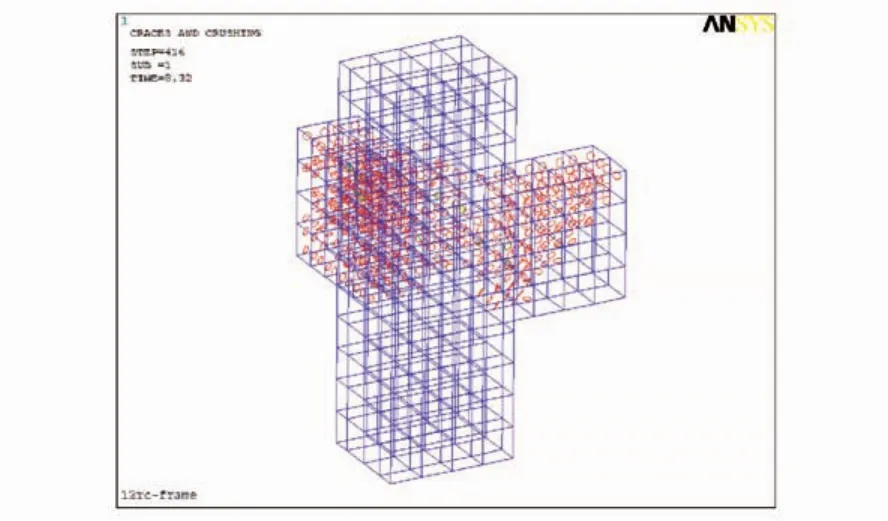
图11 混凝土开裂与压碎Fig.11 Concrete crack and crushing

4 结 论

多尺度有限元计算方法可在有限的计算资源和时间下，有针对性地获得结构宏观和微观的力学性能信息，提高计算效率。

基于能量守恒原理与材料力学理论，一维单元和三维单元可以通过多点约束方程建立耦合关系。在ANSYS软件中建立一维单元和三维单元的界面处的耦合约束方程，并通过一个悬臂柱的算例验证了这一方法。

通过对一12层RC框架结构的数值模拟，得出ANSYS多尺度模型模拟的结构整体响应与梁单元模型模拟结果和试验结果具有较高的吻合度，同时不同尺度单元之间的应力过渡也比较均匀。

［1］ Abbie B.Assessing the collapse risk of California’s existing reinforced concrete frame structures：metrics for seismic safety decisions［D］.Department of Civil and Environmental Engineering，Stanford University，2008.

［2］ Sung JK，Amr S.Characterization of shaking intensity distribution and seismic assessmentof RC buildings for the Kashmir（Pakistan）earthquake of October 2005［J］.Engineering Structures，2009，（31）：2998-3015.

［3］ Yue J，Apostolos F，Qian J，et al.Application of 1D／3D finite elements coupling for structural nonlinear analysis［J］.Journal of Central South University of Technology，2011，18（3）：451-469.

［4］ Ladeveze P.A multiscale computational approach for contact problem［J］.Computer Methods in Applied Mechanics and Engineering，2002，191（43）：4869-4891.

［5］ 林旭川，陆新征，叶列平.钢-混凝土混合框架结构多尺度分析及其建模方法［J］.计算力学学报，2010，27（3）：469-474.Lin Xuchuan，Lu Xinzheng，Ye Lieping.Multi-scale finite elementmodeling and its application in the analysis of a steel-concrete hybrid frame［J］.Chinese Journal of Computational Mechanics，2010，27（3）：469-474.（in Chinese）

［6］ 王新敏，李义强，许宏伟.ANSYS结构分析单元与应用［M］.北京：人民交通出版社，2011.Wang Xinmin，Li Yiqiang，Xu Hongwei.The element for structure analysis of ANSYS and its application［M］.Beijing：China Communications Press，2011.（in Chinese）

［7］ 吕西林，李培振，陈跃庆.12层钢筋混凝土标准框架振动台模型试验的完整数据［R］.上海：同济大学土木工程防灾国家重点实验室振动台试验室，2004.Lu Xilin，Li Peizhen，Chen Yueqing.Benchmark test of a 12-story reinforced concrete frame model on shaking table［R］.Sharghai：State Key Lab for Disaster Reduction in Civil Engineering，2004.（in Chinese）

［8］ Park R，Paulay T.Reinforced concrete structures［M］.New York：John Wiley and Sons，1975：768-770.

［9］ 中华人民共和国住房和城乡建设部.GB 50010—2010混凝土结构设计规范［S］.北京：中国建筑工业出版社，2010.Ministry of Construction of the People’s Republic of China.GB 50010—2010 Code for seismic design of buildings［S］.Beijing：China Architecture and Building Press，2010.（in Chinese）

Multi-scale Numerical Analysis on a Reinforced-concrete Frame Structure by Using ANSYS

WU Qiang1，2，*QIAN Jiang1，2HUANGWei1，2
（1.State Key Laboratory of Disaster Reductson in Civil Engineering，Tongji University，Shanghai200092，China；2.Research Institute of Structural Engineering and Disaster Reduction，Tongji University，Shanghai200092，China）

Amultiscalemodel（MSM）method was proposed based on energy conservation and themechanics theory ofmaterials.A shaking table test of a 12 story reinforced concrete frame structure was simulated by a multi-scalemodel（MSM）and a beam model（BM）contrastively.The dynamic characteristics and responses to earthquake of the structurewere calculated.The MSM results agreewith the BM results and the test results.It is indicated that the proposed method can be used in the structure analysis accurately and efficiently.

multi-scalemodel，ANSYS software，reinforced concrete frame structure

2013-05-01

科技部国家重点实验室基金项目（SLDRCE10-B-07）；国家科技支撑计划项目（2012BAJ13B02）

*联系作者，Email：wuqiang07＠163.com