超重力旋转床气相传质CFD仿真分析及实验验证

周晓伟，张新玉，杨斌，于平安

（哈尔滨工程大学动力与能源工程学院，黑龙江 哈尔滨 150001）

超重力旋转床是一种高效的强化混合与传质的新型设备，相比普通传质设备，超重力设备具有液泛速率高、停留时间短、传质系数高等多种优势，引起了工业界的密切关注，现在已广泛应用于吸收、解吸、精馏、脱氧等各个化工领域[1-5]。本文涉及的超重力旋转床用于闭式循环柴油机装置中，利用海水脱除循环尾气中的二氧化碳[6-7]。由于闭式循环柴油机常用于水下潜器，常规传质设备由于传质能力有限，在有限的空间条件下难以达到要求性能；此外由于水下运行环境不可避免地会产生倾斜，会严重影响传统依赖重力传质设备的性能。从上述两点来看，在闭式循环柴油机上采用超重力旋转床的选择比较合理。

目前关于旋转填料床的模拟研究仍然处于起步阶段，国内外有部分学者对旋转床内流场进行了仿真模拟[8-13]。对于旋转床传质性能研究，主要为实验研究及理论研究，只有少数研究人员[19-20]进行了相关传质数值仿真。本文基于CFX商业软件，利用欧拉-拉格朗日模型对旋转床内两相流场进行仿真，利用希格比的渗透模型对气相传质进行数值模拟，并通过实验进行对仿真结果进行验证。

1 物理模型及网格划分

模型如图1所示，金属丝网外径340 mm，内径198 mm，金属丝网共5层。转轴带动液体分布器高速旋转，自来水经分布器破碎成为微小颗粒后进入流体区，在金属丝网上再次剪切破碎，后由重力的作用从排水口离开。气体自进气口向上流动，最后经由上排气口排出。由于旋转丝网的原因，气体在流体区内与破碎的颗粒强烈的混合，进行逆流传质。由于气体对液滴有一定携带，与转轴相连的捕沫器以碰撞的方式捕捉这些液滴，使进入下级的气体不携带液滴。

图1 旋转床吸收器结构

利用Icem对该模型划分网格，采用非结构四面体网格，分别对金属丝网区域和其他区域划分网格。对于金属丝网区，由于网眼非常密集，通过之后设置求解器将其处理成多孔介质，其孔隙率由实际空隙率给出，网格数量约为120万个单元，网格行列式值大于0.95，最小网格角度大于24°，综合质量大于0.35。其他区域中，在靠近金属丝网、壁面、转轴及分布器处加密网格，网格数量约为110万个单元，网格行列式值大于 0.9，最小网格角度大于18°，综合质量大于0.3。两个网格区域独立划分，并通过GGI方法连接，网格单元数量共计230万个。金属丝网区网格如图2所示。

图2 金属丝网区网格

2 数学模型

采用欧拉-拉格朗日气液两相流模型，气相为连续相，液体为颗粒相。仿真假设处于恒温条件下，不计热量影响。

2.1 边界条件及计算方法

2.1.1 计算方法

计算采用欧拉-拉格朗日模型在仿真与实验工况下，液相体积分数均远小于10%，根据CFX推荐的模型选择方式，使用欧拉-拉格朗日模型是合理的；此外，相较于两相欧拉模型，欧拉-拉格朗日模型进行传热，传质方面的仿真相比两相欧拉更为精确；国内部分学者也采用欧拉-拉格朗日模型进行传热传质计算[14，16]。气相对流项采用二阶隐式求解，湍流项采用标准 k-ε两方程模型，近壁面采用标准壁面函数进行处理，湍动能与耗散率通过其对应输运方程求解湍流模型中的各个常数采用Launder推荐值[17]，采用一阶迎风格式。液相根据拉格朗日颗粒轨道模型确定液滴的运动轨迹，其中，曳力系数Cd采用Ishii & Zuber曳力模型计算，考虑了液滴在不同雷诺数下的变形及高液相份额的影响[18]。设置合适的步长，对于旋转机械CFX推荐单步步长小于转速的倒数。各个物理量保证残差下降至10−3以下。

2.1.2 边界条件

设置气相出口为压力出口。在吸收器底部设置颗粒捕捉子域对颗粒相进行吸收。设置填料区，液体分布器及转轴为运动边界，转速设定为操作转速。其他边界均设为无滑移边界，并设置对颗粒相的壁面反弹系数为 0，即液滴碰触到壁面后即沿着壁面下落而没有反弹。气相入口、入口二氧化碳体积分数、水入口等边界条件根据实际工况进行调整。

2.2 气相传质源项设置

现有主流的气液传质理论有：惠特曼的双膜理论、希格比的溶质渗透理论及丹寇沃茨的表面更新理论。经典的双膜理论认为相界面存在传质薄膜，呈层流状态，故传质系数与扩散系数D成一次方关系，而许多实验表明在超重力设备中传质系数与D的0.5～0.75次方成正比，故双膜理论并不适用于旋转床。表面更新理论认为两相表面是不断更新的，微元的更新频率为 S，在旋转床中由于液滴与填料的剪切碰撞会让相界面迅速更新，但在本文论述的用于闭式循环柴油机的旋转床中，从仿真的结果可知，多数的液滴只被一两层丝网破碎，此时更新频率S与液滴和丝网的碰撞无关，这导致更新频率S确定的困难[22]。

溶质渗透理论讨论的是气液界面至液相主体的传质，适用于液膜控制的吸收，而水吸收二氧化碳是典型的液膜控制过程。Munjal等[23-24]对旋转叶片上的层流液膜的气液传质系数进行了研究，同样通过水吸收CO2实验，发现气液传质吸收和重力的1/6方成正比，与溶质渗透理论一致。此外，液滴多数分布于金属丝网区外，为自由下落，针对此类问题的传质仿真也较多得采用了希格比溶质渗透理论[25，27]。故本文认为相比其他两种传质理论，该模型更适合使用希格比溶质渗透模型。

可以根据式（1）进行二氧化碳质量源项计算。

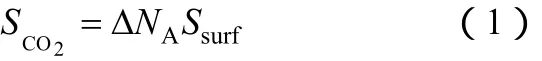
渗透模型认为气液两相接触时间很短，气体溶质从气相主体传递到液滴的过程属于非稳态过程[26]。根据渗透理论，单位时间内的质量传递量为式（2）[27]。

接触时间tp为液滴运动一个直径所需的时间，液滴运动速度 u为当前体积单元内的液滴平均速度，见式（3）[19]。

C*为液相饱和浓度，根据亨利定律，饱和浓度与气相分压正相关[25]。根据包含当前颗粒的网格单元的平均二氧化碳浓度可以计算出此时的液相饱和浓度。

C为液滴内气体溶质浓度，由于两相间的传质动力是浓度差，通过实验可以发现，尽管二氧化碳确实被吸收了一部分，但由于原本CO2占的体积分数不高，进出口的二氧化碳量的变化仅占总流量的2%～3%，这种情况下，液滴中二氧化碳浓度以接近指数的方法成长。可以近似认为，液滴中二氧化碳的含量仅为液滴停留时间的函数而与空间位置无关，故有式（4）。

式中，T为时间常量，根据两相流场得到颗粒在吸收器中的最大停留时间 tmax，液相最终的二氧化碳浓度差（根据气相浓度与气液比）及当前的液相饱和浓度可以计算得到，见式（5）。

传质面积根据在网格单元中的液滴体积分数与网格单元的体积计算，能通过包含在体积单元内的颗粒个数，计算此时单元内的传质面积，见式（6）。

由于质量源项的存在，会对动量方程、耗散率方程及湍动能方程产生的影响。通过设置被吸收物质的速度、湍动能与耗散率，可以计算这些对应方程的源项。其值为该网格单元内对应气相参数平均值。

3 结果及讨论

仿真计算条件为：进气流量127 m3/h，水流量15 m3/h，进气二氧化碳体积分数15.75%，旋转床转速800 r/min。分别对仿真的流场及二氧化碳浓度进行分析。仿真结果中 z方向为吸收器高度方向，y方向为吸收器直径方向。z=0对应吸收器进气口中心高度，z=0.4 m对应最上一级丝网之上，z=0.6 m对应位置在吸收器除雾器上。

3.1 仿真结果分析

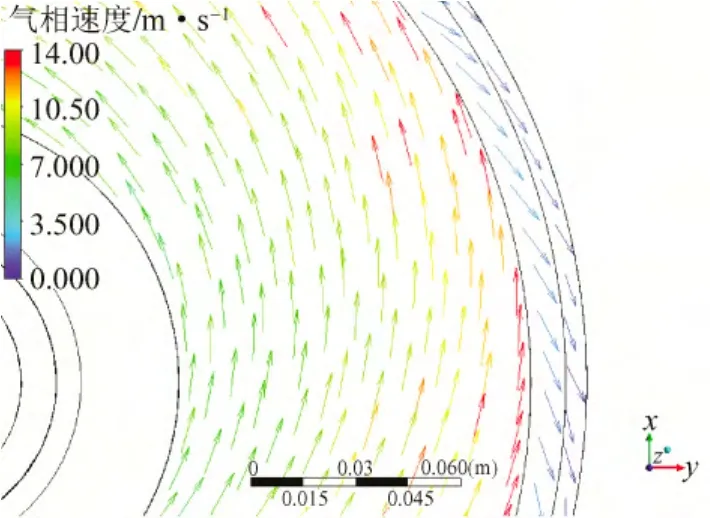
图3 第三层丝网气相速度分布

图4 Y-Z平面矢量图

3.1.1 流场结果分析

截取第三片金属丝网上速度矢量图及y- z方向矢量图（标准化后的矢量，矢量长度与速度大小无关）如图3与图4。从图3中可以看到，气相的速度大小明显受分布器影响，从丝网内缘到外缘，气相速度逐渐增大，且气流方向与旋转方向一致。在丝网外，气相速度明显变小，但旋转方向与丝网旋转方向相反。根据图4可以看出，在喷淋水的空间内（金属丝网区域），有明显的旋涡存在，而在上方除雾器区内并不存在明显的旋涡。这说明，丝网旋转带来的卷吸作用与液滴下落时对气流的作用共同造成了金属丝网区的漩涡生成，这部分漩涡延长气相在吸收器中的停留时间，并加强了气相与液相的混合，都对传质带来了益处。此外，之前论述的丝网外速度方向与丝网内速度方向相反，并且气流速度向下的原因也是因为漩涡的存在，除了y- z方向形成的漩涡，在各级金属丝网上方都形成了与丝网旋转方向相反的漩涡，共同补偿下部丝网旋转造成的真空。

3.1.2 浓度场结果分析

仿真结果中质量源项如图5所示，在靠近分布器及金属丝网上，有相对较高的源项。在靠近分布器的位置，液体刚进入流体区，此时的气液两相二氧化碳浓度差较大，传质的推动力更强；在金属丝网上，液滴被丝网捕获，在这个区域颗粒获得与丝网相同的速度，二氧化碳得以以更快的速度进行扩散，强化了传质。不同高度上沿半径方向的二氧化碳气体浓度分布如图6所示。二氧化碳浓度分布外高内地，下高上低，在z =0处由于进气气流的原因二氧化碳浓度基本是一致的。在靠近分布器处，由于质量源项较高，二氧化碳浓度降低得更快；随着气流网上运动二氧化碳逐渐被吸收，但这在z=0.1 m处不符合，主要因为进气气流流速过大对流场产生的影响。z=0.4 m以上没有丝网，故z=0.6 m处的二氧化碳浓度与z=0.4 m处二氧化碳浓度分布基本一致，只是更趋于平缓。

3.2 实验系统及实验方法

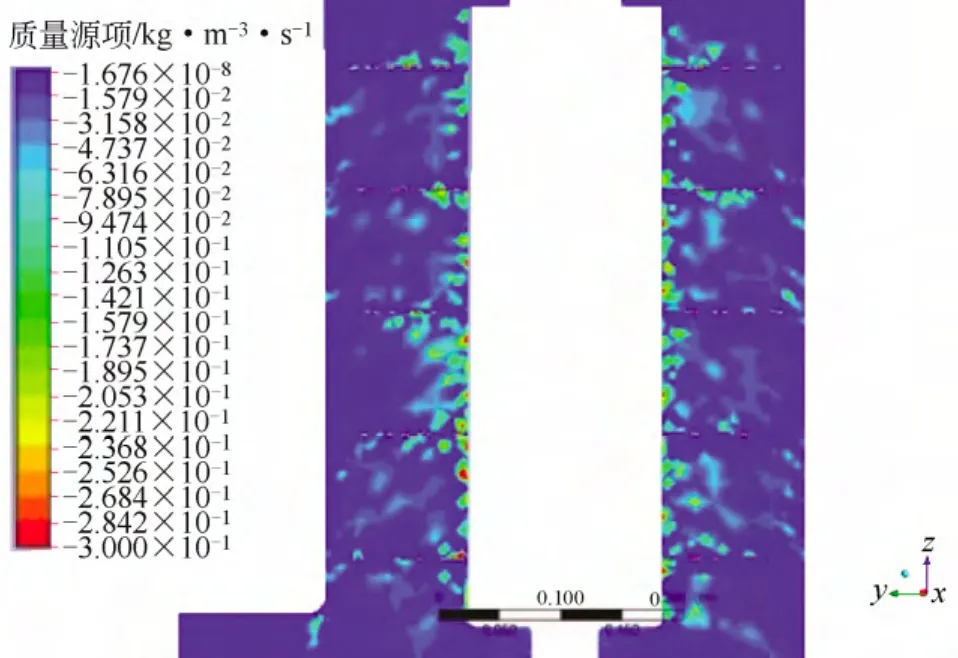
图5 y-z平面的质量源项

图6 y方向二氧化碳分布

实验测试系统基于闭式循环柴油机，如图7所示，柴油机内燃烧生成高温、含带二氧化碳的气体，经过喷淋室处理后降至室温，冷凝后，输送至二氧化碳吸收器中脱除二氧化碳，在吸收器前后分别设置二氧化碳浓度测点，使用Testo350气体成分分析仪进行测量。处理后的气体添加氩气和氧气在混合箱中充分混合后输送至柴油机进气进行燃烧，气体工质循环使用。

图7 实验台架简图

调节柴油机及旋转床吸收器操作参数进行实验，实验工况表如表1。

表1 实验工况表

3.3 实验结果与仿真结果对比

通过分析旋转床转速，柴油机功率、吸收因数A与液相传质单元数NTU的关系来考量不同操作参数对吸收能力的影响。假设平衡关系在吸收塔操作范围内可近似看成直线，且相平衡满足亨利定律，可得出以下液相传质系数计算式（7）[28]。其中 x2为入口液相中二氧化碳浓度，为0。

通过调整水流量与进气流量，改变转速来考察吸收因数与转速对传质单元数影响，如图8所示。随着水流量的增大、转速的提高，传质单元数有明显的提高，且转速具有更明显的效果，水量对传质单元数带来的效果基本是线性的，水量与转速分别使得颗粒变多、变小，都增大了气液相界面，增强了其传质能力，这和前人论文中的结论与理论是一致的。仿真与实验结果趋势基本一致，但在高转速下，仿真结果预测值较实验值低。这可能是由于以下原因：①对于颗粒直径的假设在这里并不合理；②在动平衡下，相平衡条件偏离了亨利定律。调整柴油机功率，维持水量和旋转床转速不变，考察进气二氧化碳浓度对传质单元数影响，结果如图9所示。由仿真结果和实验结果可以看出，随着进气二氧化碳的体积分数升高，传质单元数降低。

由仿真得出的结果对比试验结果，平均误差约在10%，最大误差为20.6%。这主要是在高转速工况下仿真值低于实验值，这可能与对液滴直径的预计有一定关系，采用 Long的模型可能需要选取更为合适的参数。其次，由于测量时实验仪器的读数和波动性等原因带来的误差会相对较大。并且，本文忽略了一部分影响因素，会带来一定程度对结果的偏移。总体来说实验与仿真的误差基本可以认为是可以接受的。

图8 不同转速与吸收因数下传质单元数

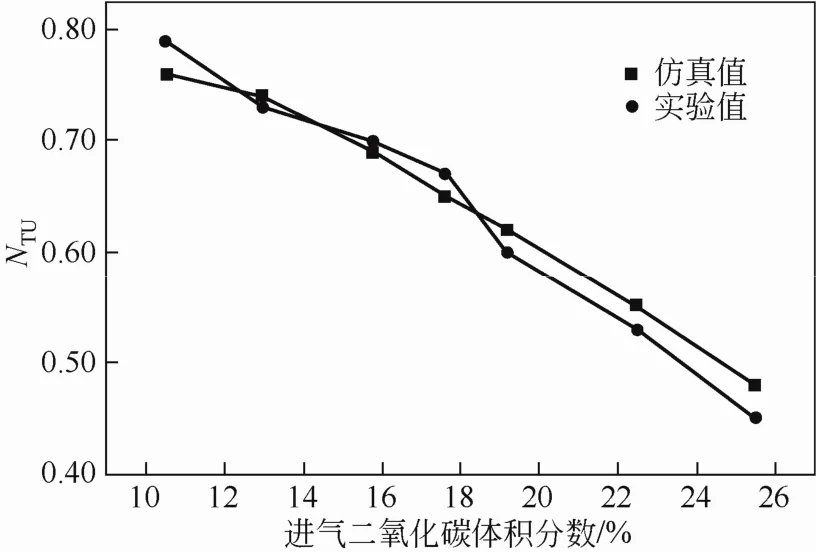
图9 不同进气二氧化碳体积分数下的传质单元数

4 结 论

通过对使用水吸收二氧化碳的超重力旋转床进行了仿真分析与实验研究。利用欧拉-拉格朗日两相流模型对流场进行仿真，根据希格比溶质渗透理论设置气相源项用来模拟二氧化碳吸收过程，在闭式循环柴油机上进行吸收因数，柴油机操作工况对吸收性能影响的分析试验并对比仿真实验结果，证明仿真的有效性。

（1）通过设置二氧化碳源项能够降低超重力床中的二氧化碳浓度。在靠近液体出口的位置和丝网中的源项数值较大，传质更剧烈。

（2）随着旋转床转速及吸收因数增加，吸收器脱除二氧化碳的能力增强。结论与前人论文论述的一致。其中，吸收器转速对吸收能力的影响更明显。

（3）仿真与实验在高转速工况下结果有一定偏差，仿真结果偏小，可能是由于对颗粒直径模型选取参数不当导致的。

（4）仿真结果与实验结果有较高的一致性，平均误差在10%左右，说明仿真对描述吸收器内传质过程的描述有一定参考意义。

符号说明

A ——吸收因数，量纲为1

C* ——液相二氧化碳饱和浓度，量纲为1

C ——液相二氧化碳浓度，量纲为1

Ct——液相当前时刻二氧化碳浓度，L/L

D ——二氧化碳在水中的扩散系数，m2/s

d ——颗粒平均直径，m

Lg——气体体积流量，L/min

Lw——液体体积流量，L/min

l ——气体总压力为1个大气压时溶解于1体积水中的二氧化碳体积，量纲为1

Mp——颗粒质量，kg

m ——相平衡常数，量纲为1

Np——颗粒数量率，s−1

NTU——液相传质单元数，量纲为1

Q ——一个大气压下二氧化碳在水中的溶解度，g/g

S ——表面更新频率，s−1

Ssurf——气液两相接触面积，m2

Sp——颗粒表面积，m2

T ——时间常数，计算值，s

t ——颗粒当前在床内停留时间，s

tmax——颗粒在床内最大停留时间，s

tp——液滴运动一个液滴直径的时间，s

U ——气相速度，m/s

up——液相速度，m/s

Vele——网格单元体积，m3

Vp——颗粒体积， m3

x2——入口液相中溶质浓度，mol/L

y1——入口气相中溶质浓度，mol/L

y2——出口气相中溶质浓度，mol/L

αgp——气液体积流量比，L/L

Ρ——气相密度，kg/m3

φp——颗粒数量，量纲为1

[1]陈建峰. 超重力技术与应用[M]. 北京：化学工业出版社，2002：26-28.

[2]Ramshaw C. Higee distillation：An example of process intensification[J]. Chem. Engrs.，2006，37（1）：63-69.

[3]Lin C，C，Jian G S. Characteristics of a rotating packed bed equipped with blade packing[J]. Separation and Purification Technology，2007，27：51-60.

[4]Ko C H，Guan C Y，Lu P，et al. Zonation of guaiacol solution in a rotating packed bed[J]. Chemical Engineering Journal，2011，171：1045-1052.

[5]高升，刘学军，王广全，等. 喷射式超重力旋转床吸收 CO2的研究[J]. 化工进展，2011，30（s1）：822-824.

[6]肖昌龙. 闭式循环柴油机性能研究[D]. 哈尔滨：哈尔滨工程大学，2009.

[7]张小青，张新玉，李晓声. 旋转填料床气液两相流场仿真[J]. 现代化工，2011，31（s1）：412-415.

[8]杨文婧. 旋转填料床流场与微混合的CFD模拟[D]. 天津：天津大学，2009.

[9]张建文，高冬霞，李亚超，等. 旋转床超重力环境下多相流传递过程研究进展[J]. 化工学报，2013，64（1）：243-251.

[10]郑碏，董立户，陈健，等. CO2捕集的吸收溶解度计算和过程模拟[J]. 化工学报，2010，61（7）：1740-1746.

[11]Chen W H，Syu Y J. Hydrogen production from water gas shift reaction in a high gravity environment using a rotating packed bed[J]. International Journal of Hydrogen Energy，2010，35：10179-10189.

[12]孙润林，向阳，初广文，等. 旋转填充床气相流场模拟与仿真[J].北京化工大学学报：自然科学版，2012，39（4）： 6-11.

[13]石鑫，向阳，文利雄，等. 基于离散相模型的旋转填充床内的流场分析[J]. 高校化学工程学报，2012，26（3）：388-394.

[14]许明，张建文，沈志刚，等. 超重力旋转床中气液两相流动与传质过程的数值模拟[J]. 北京化工大学学报：自然科学版，2004，31（5）：30-35.

[15]易飞. 超重力技术脱除二氧化碳的实验和模拟研究[D]. 北京：北京化工大学，2008.

[16]时钧，汪家鼎，余国琮，等. 化学工程手册[M]. 北京：化学工业出版社，1996：237-239.

[17]Launder B E，Spalding D B. The numerical computation of turbulent flow[J]. Computer Methods in Applied Mechanics and Engineering，1974，3（2）：269-289.

[18]Mamoru Ishii，Novak Zuber. Drag coefficient and relative velocity in bubbly，droplet or particulate flows[J]. AIChE J.，1979，25（5）：843-855.

[19]车得福，李会熊. 多相流及其应用[M]. 西安：西安交通大学出版社，2007：80-84.

[20]王文琪. 两相流动[M]. 北京：水利电力出版社，1989：28-48.

[21]Long G. Spraying theory and practice[J]. Chemical Engineering，1978，85（6）：73-77.

[22]Seader J D. Separation Process Principals[M]. New Jersey：John Wiley & Sons，2006：373-377.

[23]Munjal S，Dudukovć M P，Ramachandran P. Mass-transfer in rotating packed beds I. Development of gas-liquid and liquid-solid mass-transfer correlations[J]. Chemical Engineering Science，1989，44（10）：2245-2256.

[24]Munjal S，Dudukovć M P，Ramachandran P. Mass-transfer in rotating packed beds II. Experimental results and comparison with theory and gravity flow[J]. Chemical Engineering Science，1989，44（10）：2257-2268.

[25]郭三霞，李立清，唐琳，等. 喷淋环栅式除尘脱硫反应器的数学模拟[J]. 环境工程，2006，24（6）：48-51.

[26]Mackay D，Shiu W Y. A critical review of Henry's law constants for chemicals of environmental interest[J]. Phys. Chem. Ref.，1981，10（4）：1175-1188.

[27]Thomas K S，Robert L P，Charles R W. Mass Transfer[M]. New York：McGraw-Hill，1975：373-377.

[28]许熙，齐鸣斋，熊丹柳. 吸收塔传质单元数的表达式及选择[J]. 化工高等教育，2003，76（2）：66-68.